11.8: Tamaño del Efecto, Tamaño de la Muestra y Potencia
- Page ID
- 151780
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
En secciones anteriores he enfatizado el hecho de que el principal principio de diseño detrás de las pruebas de hipótesis estadísticas es que tratamos de controlar nuestra tasa de error Tipo I. Cuando arreglamos α=.05 estamos intentando asegurar que solo el 5% de las verdaderas hipótesis nulas sean rechazadas incorrectamente. Sin embargo, esto no quiere decir que no nos preocupen los errores de Tipo II. De hecho, desde la perspectiva del investigador, el error de no rechazar el nulo cuando en realidad es falso es extremadamente molesto. Con eso en mente, un objetivo secundario de las pruebas de hipótesis es tratar de minimizar β, la tasa de error de Tipo II, aunque no solemos hablar en términos de minimizar los errores de Tipo II. En cambio, hablamos de maximizar el poder de la prueba. Dado que el poder se define como 1−β, esto es lo mismo.
función de potencia
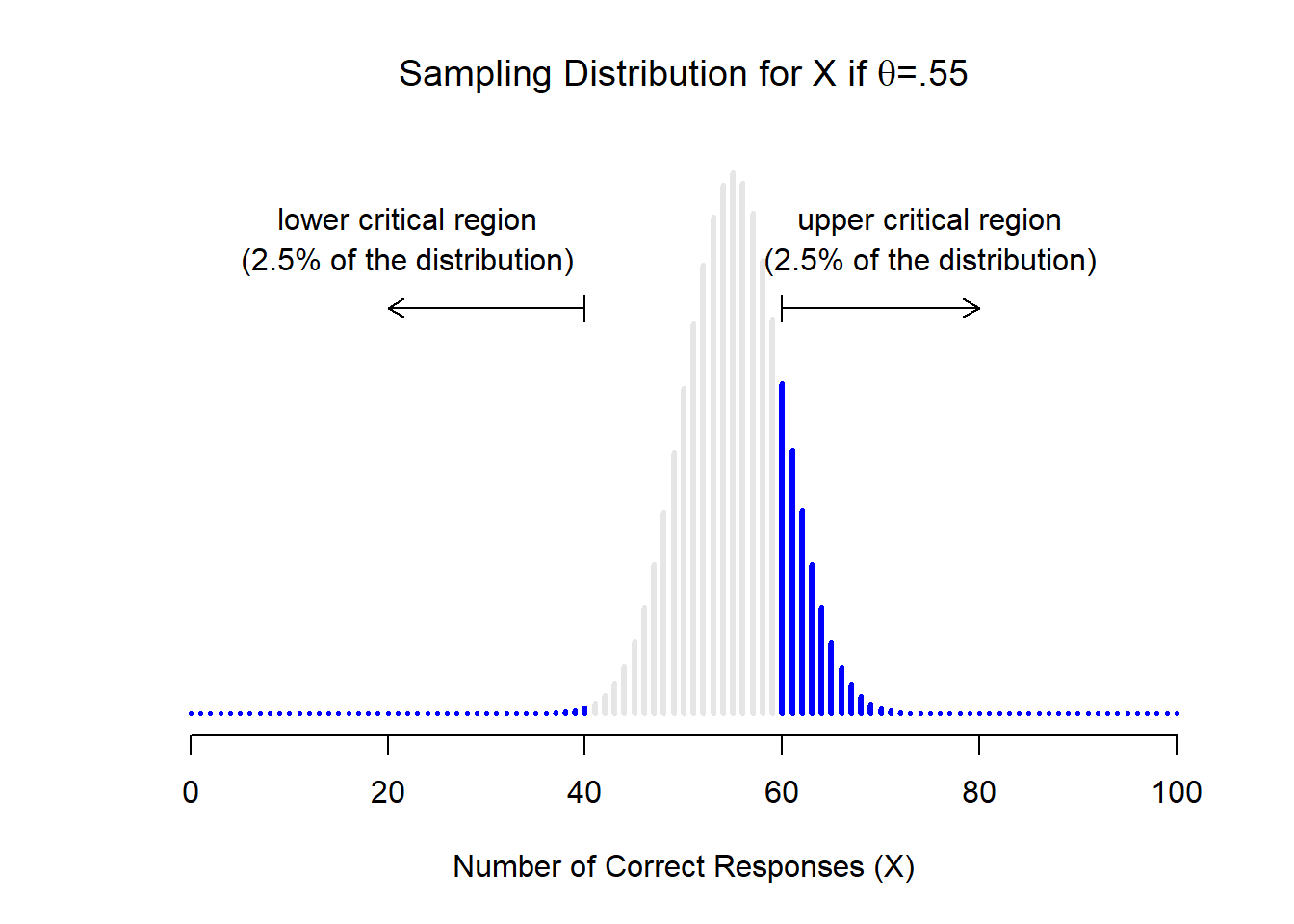
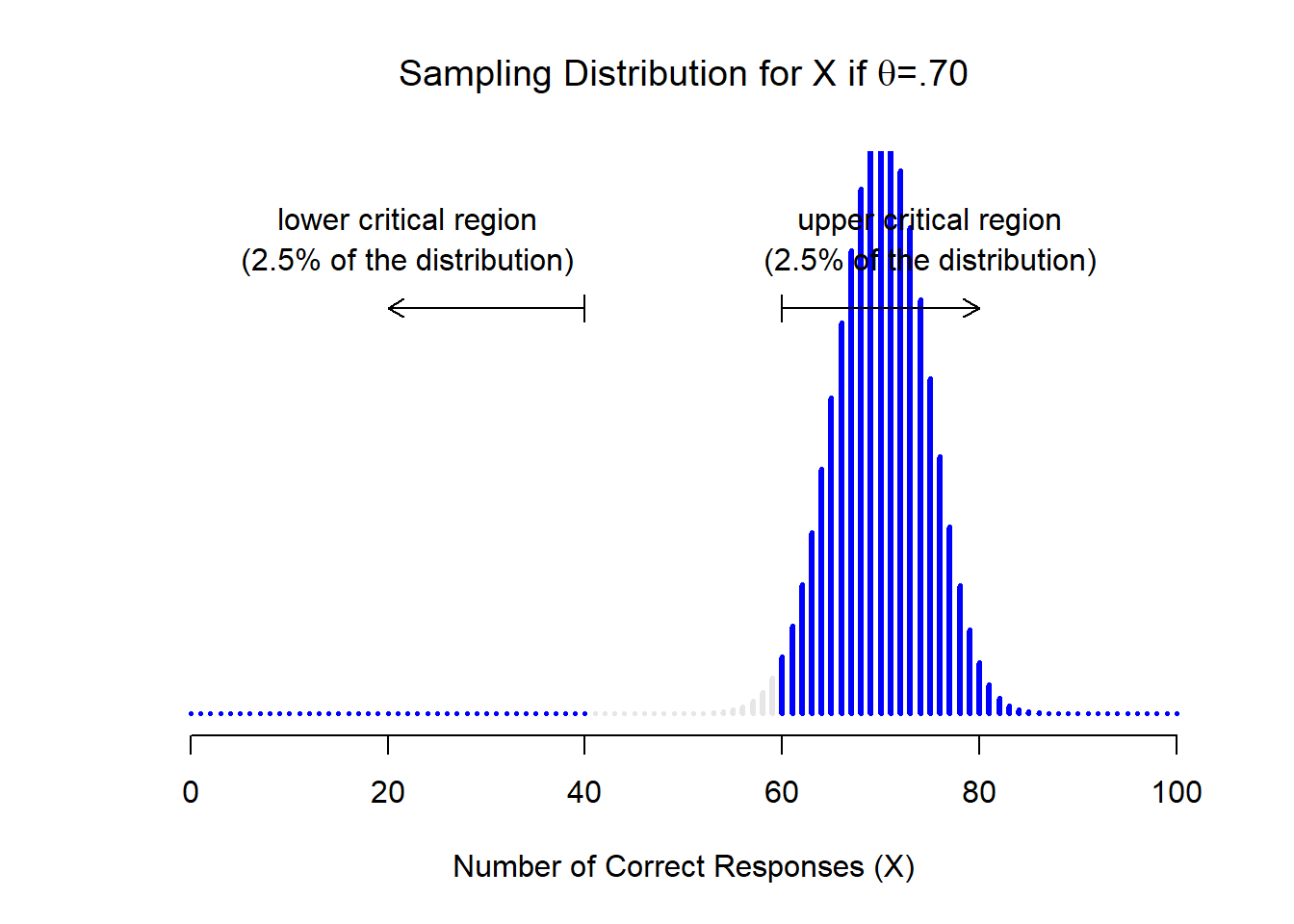
Tomemos un momento para pensar qué es realmente un error de Tipo II. Un error Tipo II ocurre cuando la hipótesis alternativa es verdadera, pero no podemos rechazar la hipótesis nula. Idealmente, podríamos calcular un solo número β que nos indique la tasa de error Tipo II, de la misma manera que podemos establecer α=.05 para la tasa de error Tipo I. Desafortunadamente, esto es mucho más complicado de hacer. Para ver esto, observe que en mi estudio ESP la hipótesis alternativa en realidad corresponde a muchos valores posibles de θ. De hecho, la hipótesis alternativa corresponde a cada valor de θ excepto 0.5. Supongamos que la verdadera probabilidad de que alguien elija la respuesta correcta es del 55% (es decir, θ=.55). Si es así, entonces la distribución de muestreo verdadera para X no es la misma que predice la hipótesis nula: el valor más probable para X es ahora 55 sobre 100. No solo eso, la distribución total del muestreo ahora se ha desplazado, como se muestra en la Figura 11.4. Las regiones críticas, por supuesto, no cambian: por definición, las regiones críticas se basan en lo que predice la hipótesis nula. Lo que estamos viendo en esta cifra es el hecho de que cuando la hipótesis nula es incorrecta, una proporción mucho mayor de la distribución de la distribución muestral cae en la región crítica. Y claro que eso es lo que debería pasar: ¡la probabilidad de rechazar la hipótesis nula es mayor cuando la hipótesis nula es realmente falsa! Sin embargo θ=.55 no es la única posibilidad consistente con la hipótesis alternativa. Supongamos que el verdadero valor de θ es en realidad 0.7. ¿Qué sucede con la distribución del muestreo cuando esto ocurre? La respuesta, que se muestra en la Figura 11.5, es que casi la totalidad de la distribución muestral se ha trasladado ahora a la región crítica. Por lo tanto, si θ=0.7 la probabilidad de que rechacemos correctamente la hipótesis nula (es decir, la potencia de la prueba) es mucho mayor que si θ=0.55. En resumen, mientras que θ=.55 y θ=.70 son ambos parte de la hipótesis alternativa, la tasa de error de Tipo II es diferente.
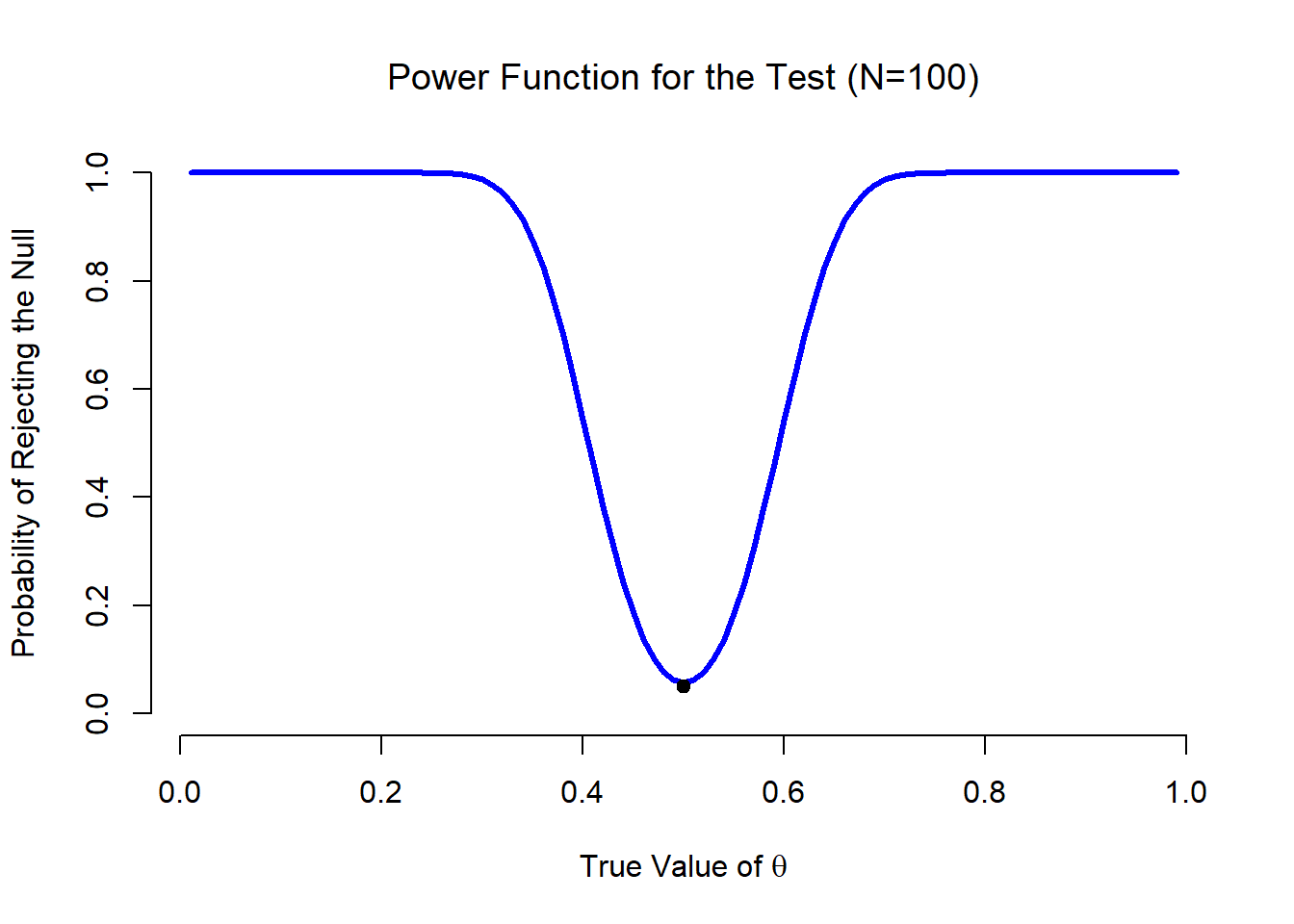
Lo que todo esto significa es que la potencia de una prueba (i.e., 1−β) depende del verdadero valor de θ. Para ilustrar esto, calculé la probabilidad esperada de rechazar la hipótesis nula para todos los valores de θ, y la representé en la Figura 11.6. Esta gráfica describe lo que generalmente se llama la función de potencia de la prueba. Es un buen resumen de lo buena que es la prueba, porque en realidad te dice la potencia (1−β) para todos los valores posibles de θ. Como puede ver, cuando el valor verdadero de θ está muy cerca de 0.5, la potencia de la prueba cae muy bruscamente, pero cuando está más lejos, la potencia es grande.
Tamaño del efecto
Dado que todos los modelos están equivocados el científico debe estar alerta a lo que es importante que esté mal. Es inapropiado preocuparse por los ratones cuando hay tigres en el extranjero
— George Box 1976
La gráfica mostrada en la Figura 11.6 captura un punto bastante básico sobre las pruebas de hipótesis. Si el verdadero estado del mundo es muy diferente de lo que predice la hipótesis nula, entonces tu poder será muy alto; pero si el verdadero estado del mundo es similar al nulo (pero no idéntico) entonces el poder de la prueba va a ser muy bajo. Por lo tanto, es útil poder tener alguna forma de cuantificar cuán “similar” es el verdadero estado del mundo a la hipótesis nula. Una estadística que hace esto se llama una medida del tamaño del efecto (por ejemplo, Cohen 1988; Ellis 2010). El tamaño del efecto se define de manera ligeramente diferente en diferentes contextos, 165 (y así esta sección solo habla en términos generales) pero la idea cualitativa que trata de capturar es siempre la misma: qué tan grande es la diferencia entre los verdaderos parámetros de población, y la valores de parámetros que son asumidos por la hipótesis nula? En nuestro ejemplo ESP, si dejamos q 0 = 0.5 denotar el valor asumido por la hipótesis nula, y dejamos q denotar el valor verdadero, entonces una simple medida del tamaño del efecto podría ser algo así como la diferencia entre el valor verdadero y nulo (es decir, θ−θ 0), o posiblemente solo la magnitud de este diferencia, abs (θ−θ 0).
| gran tamaño del efecto | tamaño pequeño del efecto | |
|---|---|---|
| resultado significativo | la diferencia es real, y de importancia práctica | la diferencia es real, pero puede que no sea interesante |
| resultado no significativo | no se observó ningún efecto | no se observó ningún efecto |
¿Por qué calcular el tamaño del efecto? Supongamos que ejecutaste tu experimento, recopilaste los datos y obtuviste un efecto significativo cuando ejecutaste tu prueba de hipótesis. ¿No basta con decir que has conseguido un efecto significativo? Seguramente ese es el punto de las pruebas de hipótesis? Bueno, algo así como. Sí, el punto de hacer una prueba de hipótesis es tratar de demostrar que la hipótesis nula está equivocada, pero eso no es lo único que nos interesa. Si la hipótesis nula afirmaba que θ=.5, y demostramos que está mal, solo hemos contado realmente la mitad de la historia. Rechazar la hipótesis nula implica que creemos que θ≠ .5, pero hay una gran diferencia entre θ=.51 y θ=.8. Si encontramos que θ=.8, entonces no sólo hemos encontrado que la hipótesis nula es incorrecta, parece estar muy equivocada. Por otro lado, supongamos que hemos rechazado con éxito la hipótesis nula, pero parece que el verdadero valor de θ es solo .51 (esto solo sería posible con un estudio grande). Claro, la hipótesis nula está equivocada, pero no está nada claro que realmente nos importe, porque el tamaño del efecto es muy pequeño. En el contexto de mi estudio del ESP todavía nos puede preocupar, ya que cualquier demostración de poderes psíquicos reales en realidad sería bastante genial 166, pero en otros contextos una diferencia de 1% no es muy interesante, aunque sea una diferencia real. Por ejemplo, supongamos que estamos viendo diferencias en los puntajes de los exámenes de secundaria entre hombres y mujeres, y resulta que los puntajes femeninos son 1% más altos en promedio que los varones. Si tengo datos de miles de estudiantes, entonces es casi seguro que esta diferencia será estadísticamente significativa, pero independientemente de lo pequeño que sea el valor p, simplemente no es muy interesante. Difícilmente querrías andar por ahí proclamando una crisis en la educación de los chicos sobre la base de una diferencia tan pequeña, ¿verdad? Es por esta razón que cada vez es más estándar (lenta, pero seguramente) reportar algún tipo de medida estándar del tamaño del efecto junto con los resultados de la prueba de hipótesis. La prueba de hipótesis en sí te dice si debes creer que el efecto que has observado es real (es decir, no solo por casualidad); el tamaño del efecto te indica si te debe importar o no.
Incrementar el poder de tu estudio
No es sorprendente que los científicos estén bastante obsesionados con maximizar el poder de sus experimentos. Queremos que nuestros experimentos funcionen, y así queremos maximizar la posibilidad de rechazar la hipótesis nula si es falsa (¡y por supuesto que usualmente queremos creer que es falsa!) Como hemos visto, un factor que influye en el poder es el tamaño del efecto. Entonces, lo primero que puedes hacer para aumentar tu potencia es aumentar el tamaño del efecto. En la práctica, lo que esto significa es que quieres diseñar tu estudio de tal manera que el tamaño del efecto se magnifice. Por ejemplo, en mi estudio de ESP podría creer que los poderes psíquicos funcionan mejor en una habitación tranquila y oscura; con menos distracciones para nublar la mente. Por lo tanto, trataría de realizar mis experimentos solo en un entorno así: si puedo fortalecer de alguna manera las habilidades ESP de las personas, entonces el verdadero valor de θ subirá 167 y por lo tanto mi tamaño de efecto será mayor. En definitiva, el diseño experimental inteligente es una forma de aumentar la potencia; porque puede alterar el tamaño del efecto.
Desafortunadamente, suele darse el caso de que incluso con el mejor de los diseños experimentales es posible que solo tengas un pequeño efecto. Quizás, por ejemplo, el ESP realmente existe, pero incluso en las mejores condiciones es muy, muy débil. En esas circunstancias, su mejor apuesta para aumentar la potencia es aumentar el tamaño de la muestra. En general, cuantas más observaciones tengas disponibles, más probable es que puedas discriminar entre dos hipótesis. Si ejecutara mi experimento ESP con 10 participantes, y 7 de ellos adivinaran correctamente el color de la tarjeta oculta, no quedarías terriblemente impresionado. Pero si lo ejecutara con 10 mil participantes y 7 mil de ellos obtuvieron la respuesta correcta, sería mucho más probable que pensaras que había descubierto algo. En otras palabras, la potencia aumenta con el tamaño de la muestra. Esto se ilustra en la Figura 11.7, que muestra la potencia de la prueba para un parámetro verdadero de θ=0.7, para todos los tamaños de muestra N de 1 a 100, donde estoy asumiendo que la hipótesis nula predice que θ 0 =0.5.
## [1] 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.11837800
## [7] 0.08257300 0.05771362 0.19643626 0.14945203 0.11303734 0.25302172
## [13] 0.20255096 0.16086106 0.29695959 0.24588947 0.38879291 0.33269435
## [19] 0.28223844 0.41641377 0.36272868 0.31341925 0.43996501 0.38859619
## [25] 0.51186665 0.46049782 0.41129777 0.52752694 0.47870819 0.58881596
## [31] 0.54162450 0.49507894 0.59933871 0.55446069 0.65155826 0.60907715
## [37] 0.69828554 0.65867614 0.61815357 0.70325017 0.66542910 0.74296156
## [43] 0.70807163 0.77808343 0.74621569 0.71275488 0.78009449 0.74946571
## [49] 0.81000236 0.78219322 0.83626633 0.81119597 0.78435605 0.83676444
## [55] 0.81250680 0.85920268 0.83741123 0.87881491 0.85934395 0.83818214
## [61] 0.87858194 0.85962510 0.89539581 0.87849413 0.91004390 0.89503851
## [67] 0.92276845 0.90949768 0.89480727 0.92209753 0.90907263 0.93304809
## [73] 0.92153987 0.94254237 0.93240638 0.92108426 0.94185449 0.93185881
## [79] 0.95005094 0.94125189 0.95714694 0.94942195 0.96327866 0.95651332
## [85] 0.94886329 0.96265653 0.95594208 0.96796884 0.96208909 0.97255504
## [91] 0.96741721 0.97650832 0.97202770 0.97991117 0.97601093 0.97153910
## [97] 0.97944717 0.97554675 0.98240749 0.97901142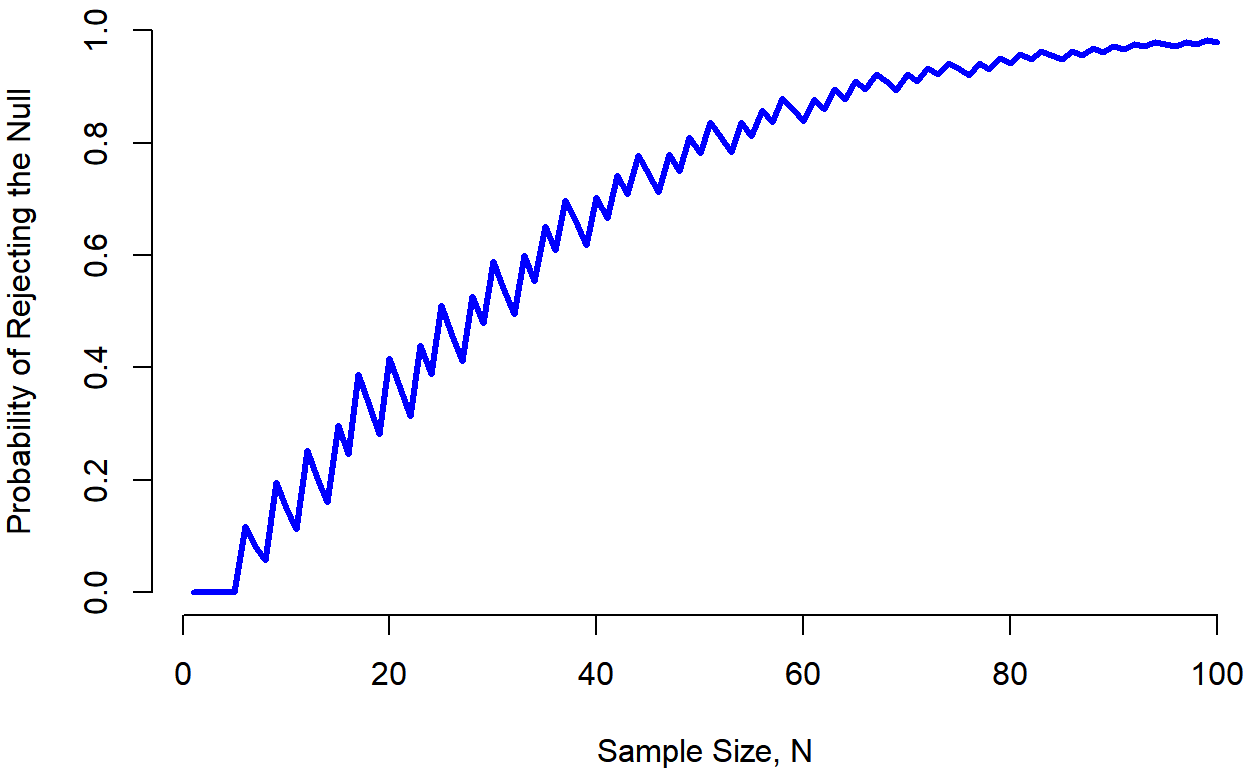
Porque el poder es importante, cada vez que estás contemplando ejecutar un experimento sería bastante útil saber cuánta potencia es probable que tengas. Nunca es posible saberlo con certeza, ya que no puedes saber cuál es el tamaño de tu efecto. Sin embargo, a menudo es posible (bueno, a veces) adivinar qué tan grande debería ser. Si es así, ¡puedes adivinar qué tamaño de muestra necesitas! Esta idea se llama análisis de potencia, y si es factible hacerlo, entonces es muy útil, ya que puede decirte algo sobre si tienes suficiente tiempo o dinero para poder ejecutar el experimento con éxito. Cada vez es más común ver a la gente argumentando que el análisis de poder debe ser una parte requerida del diseño experimental, por lo que vale la pena conocerlo. No discuto el análisis de poder en este libro, sin embargo. Esto es en parte por una razón aburrida y en parte por una sustantiva. La aburrida razón es que todavía no he tenido tiempo de escribir sobre análisis de potencia. El sustantivo es que sigo sospechando un poco del análisis de poder. Hablando como investigador, muy rara vez me he encontrado en condiciones de poder hacer uno; o bien es el caso de que (a) mi experimento es un poco no estándar y no sé cómo definir el tamaño del efecto correctamente, (b) Literalmente tengo tan poca idea sobre cuál será el tamaño del efecto que no sabría cómo interpretar las respuestas. No sólo eso, después de extensas conversaciones con alguien que hace consultoría de estadísticas para ganarse la vida (mi esposa, como sucede), no puedo evitar notar que en la práctica la única vez que alguien le pide un análisis de poder es cuando está ayudando a alguien a escribir una solicitud de subvención. En otras palabras, la única vez que un científico parece querer un análisis de poder en la vida real es cuando se ve obligado a hacerlo por un proceso burocrático. No forma parte del trabajo diario de nadie. En resumen, siempre he sido de la opinión de que si bien el poder es un concepto importante, el análisis de potencia no es tan útil como la gente lo hace sonar, excepto en los raros casos en los que (a) alguien ha descubierto cómo calcular la potencia para tu diseño experimental real y (b) tienes una bastante buena idea de cuál es probable que sea el tamaño del efecto. A lo mejor otras personas han tenido mejores experiencias que yo, pero personalmente nunca he estado en una situación en la que tanto (a) como (b) fueran ciertas. A lo mejor me convenceré de lo contrario en el futuro, y probablemente una versión futura de este libro incluiría una discusión más detallada del análisis de poder, pero por ahora esto es tanto como me siento cómodo diciendo sobre el tema.


