12.1: La prueba de bondad de ajuste χ2
- Page ID
- 151270
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)La prueba de bondad de ajuste χ 2 es una de las pruebas de hipótesis más antiguas que existen: fue inventada por Karl Pearson a principios de siglo (Pearson 1900), con algunas correcciones hechas posteriormente por Sir Ronald Fisher (Fisher 1922a). Para introducir el problema estadístico que aborda, comencemos con algo de psicología...
datos de tarjetas
A lo largo de los años, ha habido muchos estudios que muestran que los humanos tienen muchas dificultades para simular la aleatoriedad. Tratemos como fuéramos de “actuar” al azar, pensamos en términos de patrones y estructura, y así cuando se le pide que “haga algo al azar”, lo que la gente realmente hace es cualquier cosa menos al azar. En consecuencia, el estudio de la aleatoriedad humana (o no aleatoriedad, según sea el caso) abre muchas preguntas psicológicas profundas sobre cómo pensamos sobre el mundo. Con esto en mente, consideremos un estudio muy sencillo. Supongamos que le pedí a la gente que imaginara una baraja de cartas barajada y que eligiera mentalmente una carta de esta baraja imaginaria “al azar”. Después de que hayan elegido una tarjeta, les pido que seleccionen mentalmente una segunda. Para ambas opciones, lo que vamos a ver es el traje (corazones, palos, espadas o diamantes) que la gente eligió. Después de preguntar, digamos, N = 200 personas para hacer esto, me gustaría mirar los datos y averiguar si las tarjetas que la gente fingía seleccionar eran realmente aleatorias o no. Los datos están contenidos en el archivo Randomness.rdata, que contiene un solo marco de datos llamado tarjetas. Echemos un vistazo:
library( lsr )
load( "./rbook-master/data/randomness.Rdata" )
str(cards)## 'data.frame': 200 obs. of 3 variables:
## $ id : Factor w/ 200 levels "subj1","subj10",..: 1 112 124 135 146 157 168 179 190 2 ...
## $ choice_1: Factor w/ 4 levels "clubs","diamonds",..: 4 2 3 4 3 1 3 2 4 2 ...
## $ choice_2: Factor w/ 4 levels "clubs","diamonds",..: 1 1 1 1 4 3 2 1 1 4 ...Como puede ver, el marco de datos de las tarjetas contiene tres variables, una variable id que asigna un identificador único a cada participante, y las dos variables choice_1 y choice_2 que indican los trajes de tarjeta que la gente eligió. Aquí están las primeras entradas en el marco de datos:
head( cards )## id choice_1 choice_2
## 1 subj1 spades clubs
## 2 subj2 diamonds clubs
## 3 subj3 hearts clubs
## 4 subj4 spades clubs
## 5 subj5 hearts spades
## 6 subj6 clubs heartsPor el momento, centrémonos en la primera elección que la gente hizo. Usaremos la función table () para contar el número de veces que observamos a las personas eligiendo cada palo. Voy a guardar la tabla a una variable llamada observada, por razones que quedarán claras muy pronto:
observed <- table( cards$choice_1 )
observed##
## clubs diamonds hearts spades
## 35 51 64 50Esa pequeña tabla de frecuencias es bastante útil. Al mirarlo, hay una pequeña pista de que es más probable que la gente seleccione corazones que clubes, pero no es del todo obvio con solo mirarlo si eso es realmente cierto, o si esto es solo por casualidad. Entonces probablemente tendremos que hacer algún tipo de análisis estadístico para averiguarlo, que es de lo que voy a hablar en la siguiente sección.
Excelente. A partir de este momento, trataremos esta tabla como los datos que estamos buscando analizar. No obstante, ya que voy a tener que hablar de estos datos en términos matemáticos (¡perdón!) podría ser una buena idea tener claro cuál es la notación. En R, si quisiera sacar el número de personas que seleccionaron diamantes, podría hacerlo por su nombre escribiendo ["diamantes"] observados pero, dado que “diamantes” es el segundo elemento del vector observado, es igualmente efectivo referirse a él como se observa [2]. La notación matemática para esto es bastante similar, excepto que acortamos la palabra legible por humanos “observado” a la letra O, y usamos subíndices en lugar de corchetes: así que la segunda observación en nuestra tabla se escribe como se observa [2] en R, y se escribe como O 2 en matemáticas. La relación entre las descripciones en inglés, los comandos R y los símbolos matemáticos se ilustran a continuación:
| etiqueta | índice i | matemáticas. símbolo | Comando R | el valor |
|---|---|---|---|---|
| clubes ♣ | 1 | O1 | observado [1] |
35 |
| diamantes ♢ | 2 | O2 | observado [2] |
51 |
| corazones ♡ | 3 | O3 | observado [3] |
64 |
| picas ♠ | 4 | O4 | observado [4] |
50 |
Ojalá eso quede bastante claro. Tampoco vale nada que los matemáticos prefieran hablar de cosas en general en lugar de cosas específicas, por lo que también verás la notación O i, que se refiere al número de observaciones que caen dentro de la categoría i-ésima (donde i podría ser 1, 2, 3 o 4). Finalmente, si queremos referirnos al conjunto de todas las frecuencias observadas, los estadísticos agrupan todos los valores observados en un vector, al que me referiré como O.
O= (O 1, O 2, O 3, O 4)
Nuevamente, aquí no hay nada nuevo o interesante: es solo notación. Si digo que O = (35,51,64,50) lo único que estoy haciendo es describir la tabla de frecuencias observadas (es decir, observadas), pero me refiero a ella usando notación matemática, en lugar de referirme a una variable R.
hipótesis nula y la hipótesis alternativa
Como indicó el último apartado, nuestra hipótesis de investigación es que “la gente no elige cartas al azar”. Lo que vamos a querer hacer ahora es traducir esto en algunas hipótesis estadísticas, y construir una prueba estadística de esas hipótesis. La prueba que te voy a describir es la prueba de bondad de ajuste χ 2 de Pearson, y como suele ser el caso, tenemos que comenzar construyendo cuidadosamente nuestra hipótesis nula. En este caso, es bastante fácil. Primero, expresemos la hipótesis nula en palabras:
| H 0 |
|---|
| Los cuatro trajes se eligen con la misma probabilidad |
Ahora bien, porque esto es estadística, tenemos que poder decir lo mismo de manera matemática. Para ello, usemos la notación P j para referirnos a la verdadera probabilidad de que se elija el traje j-ésimo. Si la hipótesis nula es verdadera, entonces cada uno de los cuatro trajes tiene un 25% de probabilidad de ser seleccionado: en otras palabras, nuestra hipótesis nula afirma que P 1 =.25, P2=.25, P3=.25 y finalmente que P 4 =.25. Sin embargo, de la misma manera que podemos agrupar nuestras frecuencias observadas en un vector O que resume todo el conjunto de datos, podemos usar P para referirnos a las probabilidades que corresponden a nuestra hipótesis nula. Entonces si dejo que el vector P= (P 1, P 2, P 3, P 4) se refiera al conjunto de probabilidades que describen nuestra hipótesis nula, entonces tenemos
H 0:P =( .25, .25, .25, .25)
En esta instancia particular, nuestra hipótesis nula corresponde a un vector de probabilidades P en el que todas las probabilidades son iguales entre sí. Pero este no tiene por qué ser el caso. Por ejemplo, si la tarea experimental era que la gente imaginara que estaban dibujando de una baraja que tenía el doble de palos que cualquier otro palo, entonces la hipótesis nula correspondería a algo así como P= (.4, .2, .2, .2). Mientras las probabilidades sean todas números positivos, y todas sumen a 1, ellas es una elección perfectamente legítima para la hipótesis nula. Sin embargo, el uso más común de la prueba de bondad de ajuste es probar una hipótesis nula de que todas las categorías son igualmente probables, por lo que nos apegaremos a eso para nuestro ejemplo.
¿Qué pasa con nuestra hipótesis alternativa, H 1? Todo lo que realmente nos interesa es demostrar que las probabilidades involucradas no son todas idénticas (es decir, las elecciones de las personas no fueron completamente aleatorias). Como consecuencia, las versiones “amigables con el ser humano” de nuestras hipótesis se ven así:
| H 0 | H 1 |
|---|---|
| Los cuatro palos se eligen con igual probabilidad y la versión “matemática amigable” es |
Al menos una de las probabilidades de elección de juego no es .25 |
| H 0 | H 1 |
|---|---|
| P= (.25, .25, .25, .25) | P≠ (.25, .25, .25, .25) |
Convenientemente, la versión matemática de las hipótesis se parece bastante a un comando R que define un vector. Entonces tal vez lo que debería hacer es almacenar el vector P en R también, ya que casi con certeza lo vamos a necesitar más tarde. Y porque soy tan imaginativo, voy a llamar a esto probabilidades de vector R,
probabilities <- c(clubs = .25, diamonds = .25, hearts = .25, spades = .25)
probabilities## clubs diamonds hearts spades
## 0.25 0.25 0.25 0.25Estadística de prueba de “bondad de ajuste”
En este punto, tenemos nuestras frecuencias observadas O y una colección de probabilidades P correspondientes a la hipótesis nula que queremos probar. Los hemos almacenado en R como las variables observadas y probabilidades correspondientes. Lo que ahora queremos hacer es construir una prueba de la hipótesis nula. Como siempre, si queremos probar H 0 contra H 1, vamos a necesitar un estadístico de prueba. El truco básico que utiliza una prueba de bondad de ajuste es construir un estadístico de prueba que mida qué tan “cerca” están los datos a la hipótesis nula. Si los datos no se parecen a lo que “esperarías” para ver si la hipótesis nula era cierta, entonces probablemente no lo sea. Bien, si la hipótesis nula fuera cierta, ¿qué esperaríamos ver? O bien, para usar la terminología correcta, cuáles son las frecuencias esperadas. Hay N=200 observaciones, y (si el nulo es verdadero) la probabilidad de que alguno de ellos elija un corazón es P 3 =.25, así que supongo que estamos esperando 200×.25=50 corazones, ¿verdad? O, más específicamente, si dejamos que E i se refiera a “el número de respuestas de categoría i que estamos esperando si el nulo es verdadero”, entonces
E i = N×P i
Esto es bastante fácil de calcular en R:
N <- 200 # sample size
expected <- N * probabilities # expected frequencies
expected## clubs diamonds hearts spades
## 50 50 50 50Nada de lo cual es muy sorprendente: si hay 200 observaciones que pueden caer en cuatro categorías, y pensamos que las cuatro categorías son igualmente probables, entonces en promedio esperaríamos ver 50 observaciones en cada categoría, ¿verdad?
Ahora bien, ¿cómo traducimos esto en una estadística de prueba? Claramente, lo que queremos hacer es comparar el número esperado de observaciones en cada categoría (E i) con el número observado de observaciones en esa categoría (O i). Y sobre la base de esta comparación, deberíamos poder llegar a una buena estadística de prueba. Para empezar, calculemos la diferencia entre lo que la hipótesis nula esperaba que encontráramos y lo que realmente encontramos. Es decir, calculamos la puntuación de diferencia “observada menos esperada”, O i −E i. Esto se ilustra en la siguiente tabla.
| ♣ | ♢ | ♡ | ♠ | ||
| frecuencia esperada | E i | 50 | 50 | 50 | 50 |
| frecuencia observada | O i | 35 | 51 | 64 | 50 |
| puntuación de diferencia | O i −E i | -15 | 1 | 14 | 0 |
Los mismos cálculos se pueden hacer en R, utilizando nuestras variables esperadas y observadas:
observed - expected ##
## clubs diamonds hearts spades
## -15 1 14 0Independientemente de si hacemos los cálculos a mano o si los hacemos en R, está claro que la gente eligió más corazones y menos palos de los que la hipótesis nula predicha. Sin embargo, un momento de pensamiento sugiere que estas diferencias crudas no son exactamente lo que estamos buscando. Intuitivamente, se siente como que es igual de malo cuando la hipótesis nula predice muy pocas observaciones (que es lo que pasó con los corazones) como lo es cuando predice demasiadas (que es lo que pasó con los palos). Entonces es un poco raro que tengamos un número negativo para los clubes y un número positivo para los oídos. Una manera fácil de arreglar esto es cuadrar todo, para que ahora calculemos las diferencias al cuadrado, (E i −O i) 2. Como antes, podríamos hacer esto a mano, pero es más fácil hacerlo en R...
(observed - expected)^2##
## clubs diamonds hearts spades
## 225 1 196 0Ahora estamos avanzando. Lo que tenemos ahora es una colección de números que son grandes cada vez que la hipótesis nula hace una mala predicción (palos y corazones), pero son pequeños cada vez que hace uno bueno (diamantes y espadas). A continuación, por algunas razones técnicas que voy a explicar en un momento, dividamos también todos estos números por la frecuencia esperada E i, así que en realidad estamos calculando\(\dfrac{\left(E_{i}-O_{i}\right)^{2}}{E_{i}}\). Desde E i =50 para todas las categorías en nuestro ejemplo, no es un cálculo muy interesante, pero hagámoslo de todos modos. El comando R se convierte en:
(observed - expected)^2 / expected##
## clubs diamonds hearts spades
## 4.50 0.02 3.92 0.00En efecto, lo que tenemos aquí son cuatro puntuaciones diferentes de “error”, cada una de las cuales nos dice cuán grande es un “error” que hizo la hipótesis nula cuando intentamos usarla para predecir nuestras frecuencias observadas. Entonces, para convertir esto en una estadística de prueba útil, una cosa que podríamos hacer es simplemente sumar estos números. El resultado se denomina estadística de bondad de ajuste, convencionalmente conocida como X 2 o GOF. Podemos calcularlo usando este comando en R
sum( (observed - expected)^2 / expected )## [1] 8.44La fórmula para esta estadística se ve notablemente similar al comando R. Si dejamos que k se refiera al número total de categorías (es decir, k=4 para los datos de nuestras tarjetas), entonces la estadística X 2 viene dada por:
\(X^{2}=\sum_{i=1}^{k} \dfrac{\left(O_{i}-E_{i}\right)^{2}}{E_{i}}\)
Intuitivamente, está claro que si X 2 es pequeño, entonces los datos observados O i están muy cerca de lo que predijo la hipótesis nula E i, por lo que vamos a necesitar una estadística grande de X 2 para rechazar el nulo. Como hemos visto en nuestros cálculos, en nuestro conjunto de datos de tarjetas tenemos un valor de X 2 =8.44. Entonces ahora la pregunta se vuelve, ¿es esto un valor lo suficientemente grande como para rechazar el nulo?
distribución muestral del estadístico GOF (avanzado)
Para determinar si un valor particular de X 2 es lo suficientemente grande como para justificar el rechazo de la hipótesis nula, vamos a necesitar averiguar cuál sería la distribución de muestreo para X 2 si la hipótesis nula fuera cierta. Entonces eso es lo que voy a hacer en esta sección. Te mostraré con bastante detalle cómo se construye esta distribución de muestreo, y luego —en la siguiente sección— la utilizaré para construir una prueba de hipótesis. Si quieres ir al grano y estás dispuesto a tomarlo con fe de que la distribución muestral es una distribución chi-cuadrado (χ 2) con k−1 grados de libertad, puedes saltarte el resto de esta sección. No obstante, si quieres entender por qué la prueba de bondad de ajuste funciona de la manera que lo hace, sigue leyendo...
Bien, supongamos que la hipótesis nula es realmente cierta. Si es así, entonces la verdadera probabilidad de que una observación caiga en la categoría i-ésima es P i — después de todo, esa es más o menos la definición de nuestra hipótesis nula. Pensemos en lo que esto realmente significa. Si lo piensas, esto es como decir que “la naturaleza” toma la decisión sobre si la observación termina o no en la categoría i volteando una moneda ponderada (es decir, una en la que la probabilidad de obtener una cabeza es P j). Y por lo tanto, podemos pensar en nuestra frecuencia observada O i imaginando que la naturaleza volteó N de estas monedas (una por cada observación en el conjunto de datos)... y exactamente O i de ellas se acercó de cabeza. Obviamente, esta es una forma bastante extraña de pensar sobre el experimento. Pero lo que hace (espero) es recordarles que en realidad ya hemos visto este escenario antes. Es exactamente la misma configuración que dio origen a la distribución binomial en la Sección 9.4. En otras palabras, si la hipótesis nula es cierta, entonces se deduce que nuestras frecuencias observadas fueron generadas por muestreo a partir de una distribución binomial:
O i ∼Binomio (P i, N)
Ahora bien, si recuerdas de nuestra discusión sobre el teorema del límite central (Sección 10.3.3), la distribución binomial comienza a verse prácticamente idéntica a la distribución normal, especialmente cuando N es grande y cuando P i no está demasiado cerca de 0 o 1. En otras palabras, mientras N×P i sea lo suficientemente grande —o, para decirlo de otra manera, cuando la frecuencia esperada E i sea lo suficientemente grande— la distribución teórica de O i es aproximadamente normal. Mejor aún, si O i se distribuye normalmente, entonces también lo es (O i −E i)/\(\sqrt{E_{i}}\)... ya que E i es un valor fijo, restando E i y dividiendo por\(\sqrt{E_{i}}\) cambios la media y desviación estándar de la distribución normal; pero eso es todo lo que hace . Bien, entonces ahora echemos un vistazo a cuál es realmente nuestra estadística de bondad de ajuste. Lo que estamos haciendo es tomar un montón de cosas que normalmente están distribuidas, cuadrarlas y sumarlas. Espera. ¡Eso ya lo hemos visto antes también! Como comentamos en la Sección 9.6, cuando tomas un montón de cosas que tienen una distribución normal estándar (es decir, media 0 y desviación estándar 1), las cuadras, luego las sumas, entonces la cantidad resultante tiene una distribución chi-cuadrada. Entonces ahora sabemos que la hipótesis nula predice que la distribución muestral de la estadística de bondad de ajuste es una distribución chi-cuadrada. Fresco.
Hay un último detalle del que hablar, es decir, los grados de libertad. Si recuerdas de nuevo a la Sección 9.6, dije que si el número de cosas que estás sumando es k, entonces los grados de libertad para la distribución chi-cuadrada resultante son k. Sin embargo, lo que dije al inicio de esta sección es que los grados reales de libertad para la prueba de bondad de ajuste chi-cuadrado es k−1. ¿Qué pasa con eso? La respuesta aquí es que lo que se supone que debemos estar viendo es la cantidad de cosas genuinamente independientes que se están sumando. Y, como voy a hablar en la siguiente sección, a pesar de que hay k cosas que estamos agregando, solo k−1 de ellas son verdaderamente independientes; y así los grados de libertad en realidad son solo k−1. Ese es el tema de la siguiente sección. 170
Grados de libertad
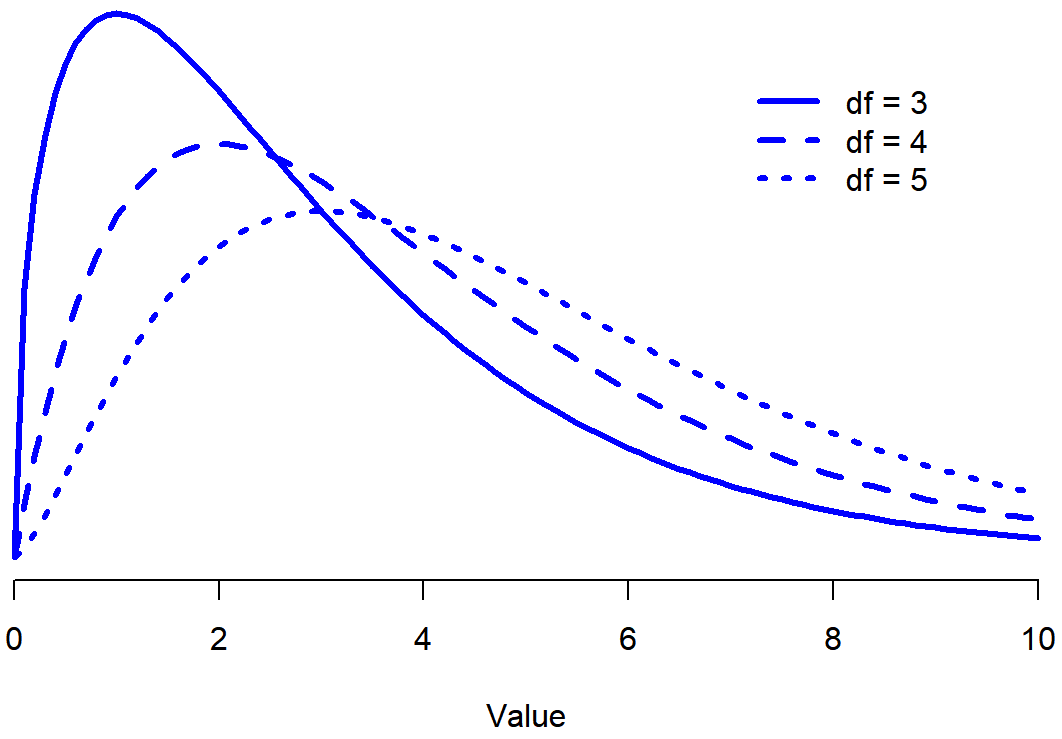
Cuando introduje la distribución chi-cuadrada en la Sección 9.6, fui un poco vago sobre lo que realmente significa “grados de libertad”. Obviamente, importa: mirando la Figura 12.1 se puede ver que si cambiamos los grados de libertad, entonces la distribución chi-cuadrada cambia de forma bastante sustancial. Pero, ¿qué es exactamente? Nuevamente, cuando introduje la distribución y expliqué su relación con la distribución normal, sí ofrecí una respuesta... es el número de “variables normalmente distribuidas” que estoy cuadrando y sumando. Pero, para la mayoría de la gente, eso es algo abstracto, y no del todo útil. Lo que realmente tenemos que hacer es tratar de entender los grados de libertad en términos de nuestros datos. Entonces aquí va.
La idea básica detrás de los grados de libertad es bastante simple: la calculas contando el número de “cantidades” distintas que se utilizan para describir tus datos; y luego restando todas las “restricciones” que esos datos deben satisfacer. 171 Esto es un poco vago, así que usemos los datos de nuestras tarjetas como ejemplo concreto. Se describen los datos utilizando cuatro números, O 1, O 2, O 3 y O 4 correspondientes a las frecuencias observadas de las cuatro categorías diferentes (corazones, palos, diamantes, espadas). Estos cuatro números son los resultados aleatorios de nuestro experimento. Pero, mi experimento en realidad tiene una restricción fija incorporada en él: el tamaño de muestra N. 172 Es decir, si sabemos cuántas personas eligieron corazones, cuántas eligieron diamantes y cuántas eligieron palos; entonces podríamos averiguar exactamente cuántas eligieron espadas. En otras palabras, aunque nuestros datos se describen usando cuatro números, en realidad solo corresponden a 4−1=3 grados de libertad. Una forma ligeramente diferente de pensarlo es notar que hay cuatro probabilidades que nos interesan (nuevamente, correspondientes a las cuatro categorías diferentes), pero estas probabilidades deben sumar a una, lo que impone una restricción. Por lo tanto, los grados de libertad son 4−1=3. Independientemente de si se quiere pensar en ello en términos de las frecuencias observadas o en términos de las probabilidades, la respuesta es la misma. En general, cuando se ejecuta la prueba de bondad de ajuste de chi-cuadrado para un experimento que involucra k grupos, entonces los grados de libertad serán k−1.
Probando la hipótesis nula
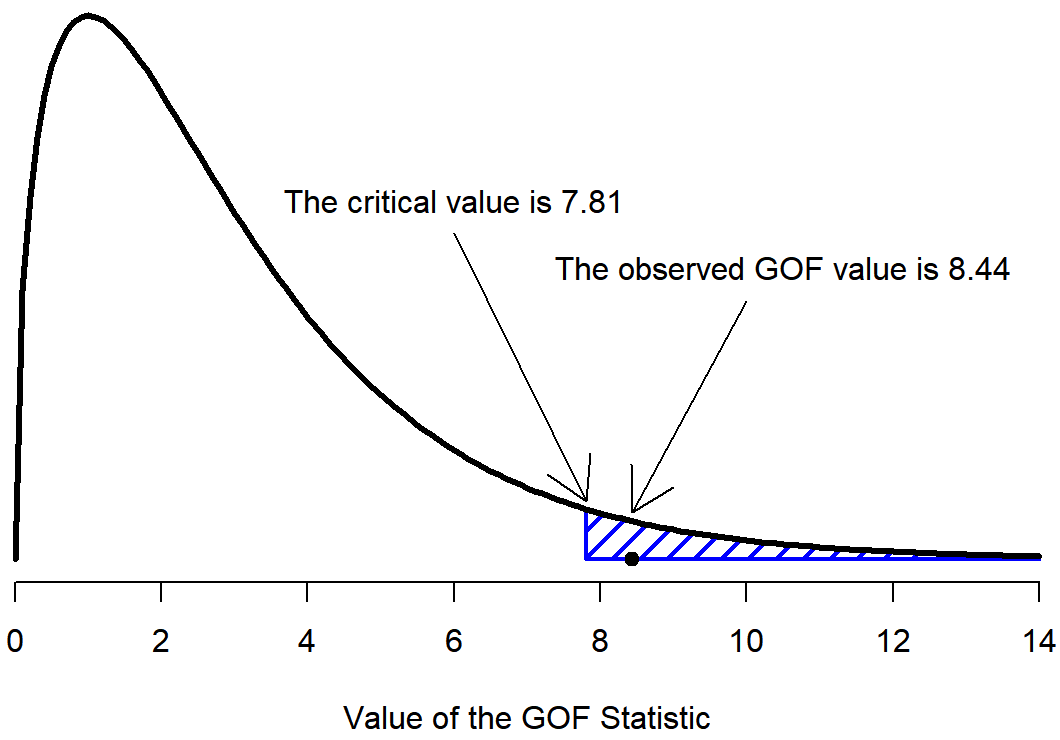
El paso final en el proceso de construcción de nuestra prueba de hipótesis es averiguar cuál es la región de rechazo. Es decir, lo que los valores de X 2 conducirían es rechazar la hipótesis nula. Como vimos anteriormente, grandes valores de X2 implican que la hipótesis nula ha hecho un mal trabajo al predecir los datos de nuestro experimento, mientras que los valores pequeños de X2 implican que en realidad se ha hecho bastante bien. Por lo tanto, una estrategia bastante sensata sería decir que hay algún valor crítico, tal que si X 2 es mayor que el valor crítico rechazamos el nulo; pero si X 2 es menor que este valor conservamos el nulo. En otras palabras, utilizar el lenguaje que introdujimos en el Capítulo @ref (hipotesistar la prueba de bondad de ajuste chi-cuadrado es siempre una prueba unilateral. Bien, entonces todo lo que tenemos que hacer es averiguar cuál es este valor crítico. Y es bastante sencillo. Si queremos que nuestra prueba tenga un nivel de significancia de α=.05 (es decir, estamos dispuestos a tolerar una tasa de error Tipo I del 5%), entonces tenemos que elegir nuestro valor crítico para que solo haya un 5% de posibilidades de que X 2 pueda llegar a ser tan grande si la hipótesis nula es cierta. Es decir, queremos el percentil 95 de la distribución muestral. Esto se ilustra en la Figura 12.2.
Ah, pero —te escucho preguntar— ¿cómo calculo el percentil 95 de una distribución chi-cuadrada con k−1 grados de libertad? Si tan solo R tuviera alguna función, llamada... oh, no sé, qchisq ()... eso te permitiría calcular este percentil (ver Capítulo 9 si lo has olvidado). Así...
qchisq( p = .95, df = 3 )## [1] 7.814728Entonces, si nuestro estadístico X 2 es mayor que 7.81 más o menos, entonces podemos rechazar la hipótesis nula. Ya que en realidad calculamos eso antes (es decir, X 2 =8.44) podemos rechazar el nulo. Si queremos un valor p exacto, podemos calcularlo usando la función pchisq ():
pchisq( q = 8.44, df = 3, lower.tail = FALSE )## [1] 0.03774185Esto es ojalá bastante sencillo, siempre y cuando recuerdes que la forma “p” de las funciones de distribución de probabilidad en R siempre calcula la probabilidad de obtener un valor menor que el valor que ingresaste (en este caso 8.44). Queremos lo contrario: la probabilidad de obtener un valor de 8.44 o más. Por eso le dije a R que usara la cola superior, no la cola inferior. Dicho esto, suele ser más fácil calcular el valor p de esta manera:
1-pchisq( q = 8.44, df = 3 )## [1] 0.03774185Entonces, en este caso rechazaríamos la hipótesis nula, ya que p<.05. Y eso es, básicamente. Ya conoces “La prueba de χ 2 de Pearson para la bondad del ajuste”. Suerte.
Haciendo la prueba en R
Dios, caray. Aunque sí logramos hacer todo en R mientras estábamos pasando por ese pequeño ejemplo, más bien se siente como si estuviéramos escribiendo demasiadas cosas en la caja mágica de computación. Y odio escribir. No es sorprendente que R proporcione una función que hará todos estos cálculos por usted. De hecho, hay varias formas diferentes de hacerlo. La que la mayoría de la gente usa es la función chisq.test (), que viene con cada instalación de R. Te mostraré cómo usar la función chisq.test () más adelante (en la Sección @ref (chisq.test), pero para empezar te voy a mostrar la función GoodnessOfFitTest () en el paquete lsr, porque produce salida que creo que es más fácil de entender para los principiantes. Es bastante sencillo: nuestros datos brutos se almacenan en la variable cards$choice_1, ¿verdad? Si quieres probar la hipótesis nula de que los cuatro palos son igualmente probables, entonces (suponiendo que tengas el paquete lsr cargado) todo lo que tienes que hacer es escribir esto:
goodnessOfFitTest( cards$choice_1 ) ##
## Chi-square test against specified probabilities
##
## Data variable: cards$choice_1
##
## Hypotheses:
## null: true probabilities are as specified
## alternative: true probabilities differ from those specified
##
## Descriptives:
## observed freq. expected freq. specified prob.
## clubs 35 50 0.25
## diamonds 51 50 0.25
## hearts 64 50 0.25
## spades 50 50 0.25
##
## Test results:
## X-squared statistic: 8.44
## degrees of freedom: 3
## p-value: 0.038R luego ejecuta la prueba e imprime varias líneas de texto. Voy a pasar por la salida línea por línea, para que puedas asegurarte de que entiendes lo que estás viendo. Las dos primeras líneas solo te están diciendo cosas que ya sabes:
Chi-square test against specified probabilities
Data variable: cards$choice_1 La primera línea nos dice qué tipo de prueba de hipótesis ejecutamos, y la segunda línea nos dice el nombre de la variable en la que la ejecutamos. Después de eso viene una declaración de cuáles son las hipótesis nulas y alternativas:
Hypotheses:
null: true probabilities are as specified
alternative: true probabilities differ from those specified
Para un principiante, es un poco útil tener esto como parte de la salida: es un buen recordatorio de cuáles son tus hipótesis nulas y alternativas. Sin embargo, no se acostumbre a ver esto. La gran mayoría de las pruebas de hipótesis en R no son tan amables con los novatos. La mayoría de las funciones R están escritas bajo el supuesto de que ya entiendes la herramienta estadística que estás usando, por lo que no se molestan en incluir una declaración explícita de la hipótesis nula y alternativa. La única razón por la que GoodnessOffitTest () realmente te da esto es que lo escribí pensando en los novatos.
La siguiente parte de la salida muestra la comparación entre las frecuencias observadas y las frecuencias esperadas:
Descriptives:
observed freq. expected freq. specified prob.
clubs 35 50 0.25
diamonds 51 50 0.25
hearts 64 50 0.25
spades 50 50 0.25La primera columna muestra cuáles fueron las frecuencias observadas, la segunda columna muestra las frecuencias esperadas de acuerdo con la hipótesis nula, y la tercera columna te muestra cuáles eran realmente las probabilidades según el nulo. Para los usuarios novatos, creo que esto es útil: puedes mirar esta parte de la salida y verificar que tenga sentido: si no es así podrías haber escrito algo incorrectamente.
La última parte de la salida es lo “importante”: es el resultado de la propia prueba de hipótesis. Hay tres números clave que deben reportarse: el valor del estadístico X 2, los grados de libertad y el valor p:
Test results:
X-squared statistic: 8.44
degrees of freedom: 3
p-value: 0.038 Observe que estos son los mismos números que se nos ocurrieron al hacer los cálculos el largo camino.
Especificar una hipótesis nula diferente
En este punto tal vez te estés preguntando qué hacer si quieres ejecutar una prueba de bondad de ajuste, pero tu hipótesis nula no es que todas las categorías sean igualmente probables. Por ejemplo, supongamos que alguien había hecho la predicción teórica de que la gente debería elegir tarjetas rojas 60% de las veces, y tarjetas negras 40% de las veces (no tengo idea de por qué predecirías eso), pero no tenía otras preferencias. Si ese fuera el caso, la hipótesis nula sería esperar que el 30% de las opciones fueran corazones, 30% que fueran diamantes, 20% sean espadas y 20% sean palos. Esto me parece una teoría tonta, y es bastante fácil probarla usando nuestros datos. Todo lo que tenemos que hacer es especificar las probabilidades asociadas a la hipótesis nula. Creamos un vector como este:
nullProbs <- c(clubs = .2, diamonds = .3, hearts = .3, spades = .2)
nullProbs## clubs diamonds hearts spades
## 0.2 0.3 0.3 0.2Ahora que tenemos una hipótesis nula explícitamente especificada, la incluimos en nuestro comando. Esta vez voy a usar los nombres de los argumentos correctamente. La variable data corresponde al argumento x, y las probabilidades según la hipótesis nula corresponden al argumento p. Entonces nuestro comando es:
goodnessOfFitTest( x = cards$choice_1, p = nullProbs )
##
## Chi-square test against specified probabilities
##
## Data variable: cards$choice_1
##
## Hypotheses:
## null: true probabilities are as specified
## alternative: true probabilities differ from those specified
##
## Descriptives:
## observed freq. expected freq. specified prob.
## clubs 35 40 0.2
## diamonds 51 60 0.3
## hearts 64 60 0.3
## spades 50 40 0.2
##
## Test results:
## X-squared statistic: 4.742
## degrees of freedom: 3
## p-value: 0.192Como se puede ver la hipótesis nula y las frecuencias esperadas son diferentes a lo que fueron la última vez. Como consecuencia, nuestro estadístico de prueba X 2 es diferente, y nuestro valor p también es diferente. Molesto, el valor p es .192, así que no podemos rechazar la hipótesis nula. Lamentablemente, a pesar de que la hipótesis nula corresponde a una teoría muy tonta, estos datos no aportan suficiente evidencia en su contra.
reportar los resultados de la prueba
Entonces ahora ya sabes cómo funciona la prueba, y sabes cómo hacer la prueba usando una maravillosa caja mágica de computación. Lo siguiente que debes saber es cómo escribir los resultados. Después de todo, ¡no tiene sentido diseñar y ejecutar un experimento y luego analizar los datos si no se lo cuentas a nadie! Entonces, hablemos ahora de lo que debes hacer al reportar tu análisis. Sigamos con nuestro ejemplo de tarjeta-trajes. Si quisiera escribir este resultado para un artículo o algo así, la forma convencional de reportarlo sería escribir algo como esto:
De los 200 participantes en el experimento, 64 seleccionaron corazones para su primera elección, 51 diamantes seleccionados, 50 espadas seleccionadas y 35 palos seleccionados. Se realizó una prueba de bondad de ajuste de chi-cuadrado para comprobar si las probabilidades de elección eran idénticas para los cuatro trajes. Los resultados fueron significativos (χ 2 (3) =8.44, p<.05), sugiriendo que las personas no seleccionaron trajes puramente al azar.
Esto es bastante sencillo, y ojalá parezca bastante poco notable. Dicho esto, hay algunas cosas que debes tener en cuenta sobre esta descripción:
- La prueba estadística va precedida por la estadística descriptiva. Es decir, le dije al lector algo sobre cómo se ven los datos antes de pasar a hacer la prueba. En general, esta es una buena práctica: recuerda siempre que tu lector no conoce tus datos en ningún lado tan bien como tú. Entonces, a menos que se lo describas adecuadamente, las pruebas estadísticas no tendrán ningún sentido para ellos, y se frustrarán y llorarán.
- La descripción te dice cuál es la hipótesis nula que se está probando. Para ser honestos, los escritores no siempre hacen esto, pero a menudo es una buena idea en aquellas situaciones en las que existe cierta ambigüedad; o cuando no puedes confiar en que tus lectores estén íntimamente familiarizados con las herramientas estadísticas que estás usando. Muy a menudo el lector puede no conocer (o recordar) todos los detalles de la prueba que estás usando, ¡así que es una especie de cortesía “recordarles”! En lo que respecta a la prueba de bondad de ajuste, generalmente puedes confiar en que una audiencia científica sepa cómo funciona (ya que está cubierta en la mayoría de las clases de estadísticas de introducción). Sin embargo, sigue siendo una buena idea ser explícito sobre la afirmación de la hipótesis nula (¡brevemente!) porque la hipótesis nula puede ser diferente dependiendo de para qué estés usando la prueba. Por ejemplo, en el ejemplo de cartas mi hipótesis nula era que las cuatro probabilidades de palo eran idénticas (es decir, P 1 =P 2 =P 3 =P 4 =0.25), pero no hay nada especial en esa hipótesis. Podría fácilmente haber probado la hipótesis nula de que P 1 =0.7 y P 2 =P 3 =P 4 =0.1 usando una prueba de bondad de ajuste. Por lo que es útil para el lector si le explicas cuál era tu hipótesis nula. También, fíjate que describí la hipótesis nula en palabras, no en matemáticas. Eso es perfectamente aceptable. Puedes describirlo en matemáticas si quieres, pero como la mayoría de los lectores encuentran las palabras más fáciles de leer que los símbolos, la mayoría de los escritores tienden a describir el nulo usando palabras si pueden.
- Se incluye un “bloque de estadísticas”. Al informar los resultados de la prueba en sí, no solo dije que el resultado era significativo, incluí un “bloque estadístico” (es decir, la parte densa de aspecto matemático entre paréntesis), que reporta todos los datos estadísticos “brutos”. Para la prueba de bondad de ajuste de chi-cuadrado, la información que se informa es el estadístico de prueba (que el estadístico de bondad de ajuste fue 8.44), la información sobre la distribución utilizada en la prueba (χ 2 con 3 grados de libertad, que generalmente se acorta a χ 2 (3)), y luego el información sobre si el resultado fue significativo (en este caso p<.05). La información particular que necesita para entrar en el bloque stat es diferente para cada prueba, y así cada vez que presente una nueva prueba te mostraré cómo debería ser el bloque stat. 173 Sin embargo, el principio general es que siempre se debe proporcionar la información suficiente para que el lector pueda verificar los resultados de las pruebas ellos mismos si realmente quisieran.
- Se interpretan los resultados. Además de indicar que el resultado fue significativo, proporcioné una interpretación del resultado (es decir, que la gente no eligió al azar). Esto también es una amabilidad para el lector, porque les dice algo sobre lo que deberían creer sobre lo que está pasando en tus datos. Si no incluyes algo como esto, es muy difícil para tu lector entender lo que está pasando. 174
Como con todo lo demás, tu preocupación primordial debería ser que le expliques las cosas a tu lector. Recuerda siempre que el punto de reportar tus resultados es comunicarte a otro ser humano. No puedo decirte cuántas veces he visto la sección de resultados de un reportaje o de una tesis o incluso de un artículo científico que es sólo un galimatías, porque el escritor se ha centrado únicamente en asegurarse de que han incluido todos los números, y se ha olvidado de comunicarse realmente con el lector humano.
comentario sobre notación estadística (avanzado)
Satanás se deleita por igual en las estadísticas y en citar las escrituras
— H.G. Wells
Si has estado leyendo muy de cerca, y eres tanto pedante matemático como yo, hay una cosa sobre la forma en que escribí la prueba de chi-cuadrado en la última sección que podría estar molestándote un poco. Hay algo que se siente un poco mal al escribir “χ 2 (3) =8.44”, podrías estar pensando. Después de todo, es la estadística de bondad de ajuste la que es igual a 8.44, entonces ¿no debería haber escrito X 2 =8.44 o tal vez GOF=8.44? Esto parece estar fusionando la distribución muestral (i.e., χ 2 con df=3) con el estadístico de prueba (i.e., X 2). Lo más probable es que pensaras que era un error tipográfico, ya que χ y X se ven bastante similares. Por extraño que no lo sea. Escribir χ 2 (3) =8.44 es esencialmente una forma altamente condensada de escribir “la distribución muestral del estadístico de prueba es χ 2 (3), y el valor del estadístico de prueba es 8.44”.
En cierto sentido, esto es un poco estúpido. Hay muchas estadísticas de prueba diferentes que resultan tener una distribución de muestreo de chi-cuadrado: el estadístico X 2 que hemos utilizado para nuestra prueba de bondad de ajuste es solo uno de muchos (aunque uno de los más comúnmente encontrados). En un mundo sensato y perfectamente organizado, siempre tendríamos un nombre separado para la estadística de prueba y la distribución de muestreo: de esa manera, el propio bloque estadístico te diría exactamente qué era lo que el investigador había calculado. A veces esto sucede. Por ejemplo, el estadístico de prueba utilizado en la prueba de bondad de ajuste de Pearson está escrito X 2; pero hay una prueba estrechamente relacionada conocida como la prueba G 175, en la que el estadístico de prueba se escribe como G. Como sucede, la prueba de bondad de ajuste de Pearson y la prueba G prueban el mismo nulo hipótesis; y la distribución de muestreo es exactamente la misma (es decir, chi-cuadrado con k−1 grados de libertad). Si hubiera hecho una prueba G para los datos de las tarjetas en lugar de una prueba de bondad de ajuste, entonces habría terminado con una estadística de prueba de G=8.65, que es ligeramente diferente del valor X 2 =8.44 que obtuve antes; y produce un valor p ligeramente menor de p=.034. Supongamos que la convención era reportar el estadístico de prueba, luego la distribución de muestreo, y luego el valor p. Si eso fuera cierto, entonces estas dos situaciones producirían bloques de estadísticas diferentes: mi resultado original sería escrito X 2 =8.44, χ 2 (3), p=.038, mientras que la nueva versión usando la prueba G se escribiría como G=8.65, χ 2 (3), p=.034. Sin embargo, usando el estándar de reporte condensado, el resultado original se escribe χ 2 (3) =8.44, p=.038, y el nuevo se escribe χ 2 (3) =8.65, p=.034, y así que en realidad no está claro qué prueba ejecuté realmente.
Entonces, ¿por qué no vivimos en un mundo en el que el contenido del bloque stat especifica de manera única qué pruebas se realizaron? La razón profunda es que la vida es desordenada. Nosotros (como usuarios de herramientas estadísticas) queremos que sea agradable y ordenado y organizado... queremos que se diseñe, como si se tratara de un producto. Pero no es así como funciona la vida: la estadística es una disciplina intelectual tanto como cualquier otra, y como tal es un proyecto masivamente distribuido, parcialmente colaborativo y parcialmente competitivo que nadie entiende realmente del todo. Las cosas que tú y yo usamos como herramientas de análisis de datos no fueron creadas por una Ley de los Dioses de la Estadística; fueron inventadas por mucha gente diferente, publicadas como artículos en revistas académicas, implementadas, corregidas y modificadas por muchas otras personas, y luego explicadas a los estudiantes en libros de texto por alguien más. Como consecuencia, hay muchas estadísticas de prueba que ni siquiera tienen nombres; y como consecuencia solo se les da el mismo nombre que la distribución de muestreo correspondiente. Como veremos más adelante, cualquier estadística de prueba que siga una distribución de χ 2 se denomina comúnmente “estadística chi-cuadrada”; cualquier cosa que siga a una distribución t se llama “estadística t” y así sucesivamente. Pero, como ilustra el ejemplo X 2 versus G, dos cosas diferentes con la misma distribución muestral siguen siendo, bueno, diferentes.
Como consecuencia, a veces es una buena idea tener claro cuál fue la prueba real que ejecutaste, especialmente si estás haciendo algo inusual. Si solo dices “prueba de chi-cuadrado”, en realidad no está claro de qué prueba estás hablando. Si bien, dado que las dos pruebas de chi-cuadrado más comunes son la prueba de bondad de ajuste y la prueba de independencia (Sección 12.2), la mayoría de los lectores con entrenamiento de estadísticas probablemente puedan adivinar. Sin embargo, es algo de lo que hay que tener en cuenta.


