17.5: El valor p es una mentira.
( \newcommand{\kernel}{\mathrm{null}\,}\)
El pastel es una mentira.
El pastel es una mentira.
El pastel es una mentira.
El pastel es una mentira.
— Portal 262
Bien, en este punto podrías estar pensando que el verdadero problema no es con las estadísticas ortodoxas, solo el estándar p<.05. En un sentido, eso es cierto. La recomendación que da Johnson (2013) no es que “todos deben ser bayesianos ahora”. En cambio, la sugerencia es que sería más prudente cambiar el estándar convencional a algo así como un nivel p<.01. Esa no es una visión irrazonable de tomar, pero en mi opinión el problema es un poco más severo que eso. En mi opinión, hay un problema bastante grande integrado en la forma en que se construyen la mayoría (pero no todas) las pruebas de hipótesis ortodoxas. Son groseramente ingenuos acerca de cómo los humanos realmente investigan, y debido a esto la mayoría de los valores p están equivocados.
Suena como una afirmación absurda, ¿verdad? Bueno, considera el siguiente escenario. Se te ha ocurrido una hipótesis de investigación realmente emocionante y diseñas un estudio para probarla. Eres muy diligente, por lo que haces un análisis de potencia para determinar cuál debería ser tu tamaño de muestra, y ejecutas el estudio. Ejecutas tu prueba de hipótesis y saca un valor p de 0.072. Realmente jodidamente molesto, ¿verdad?
¿Qué debes hacer? Aquí hay algunas posibilidades:
- Concluyes que no hay ningún efecto, e intentas publicarlo como resultado nulo
- Adivina que podría haber un efecto, e intenta publicarlo como un resultado “borderline significant”
- Te rindes y pruebes un nuevo estudio
- Recopilas algunos datos más para ver si el valor p sube o (¡preferiblemente!) cae por debajo del criterio “mágico” de p<.05
¿Cuál elegirías? Antes de seguir leyendo, les exhorto a que se tomen un tiempo para pensarlo. Sé honesto contigo mismo. Pero no te estreses demasiado por ello, porque estás jodido sin importar lo que elijas. Basado en mis propias experiencias como autor, revisor y editor, así como historias que he escuchado de otros, esto es lo que sucederá en cada caso:
- Empecemos con la opción 1. Si intentas publicarlo como resultado nulo, el artículo tendrá problemas para ser publicado. Algunos revisores pensarán que p=.072 no es realmente un resultado nulo. Ellos argumentarán que es límite significativo. Otros revisores estarán de acuerdo en que es un resultado nulo, pero afirmarán que aunque algunos resultados nulos sean publicables, el tuyo no lo es. Uno o dos revisores podrían incluso estar de tu lado, pero estarás peleando una batalla cuesta arriba para lograrlo.
- Bien, pensemos en la opción número 2. Supongamos que intenta publicarlo como un resultado límite significativo. Algunos revisores afirmarán que es un resultado nulo y no debe publicarse. Otros afirmarán que la evidencia es ambigua, y que debes recolectar más datos hasta obtener un resultado significativo claro. Nuevamente, el proceso de publicación no te favorece.
- Dadas las dificultades para publicar un resultado “ambiguo” como p=.072, la opción número 3 puede parecer tentadora: darse por vencido y hacer otra cosa. Pero esa es una receta para el suicidio de carrera. Si te rindes y pruebas un nuevo proyecto más cada vez que te encuentras ante la ambigüedad, tu trabajo nunca será publicado. Y si estás en la academia sin un registro de publicación puedes perder tu trabajo. Entonces esa opción está fuera.
- Parece que estás atascado con la opción 4. No tienes resultados concluyentes, por lo que decides recolectar algunos datos más y volver a ejecutar el análisis. Parece sensato, pero desafortunadamente para ti, si haces esto todos tus valores p ahora son incorrectos. Todos ellos. No solo los valores p que calculaste para este estudio. Todos ellos. Todos los valores p que calculaste en el pasado y todos los valores p que calcularás en el futuro. Afortunadamente, nadie se dará cuenta. Te publicarán y habrás mentido.
Espera, ¿qué? ¿Cómo puede ser cierta esa última parte? Quiero decir, suena como una estrategia perfectamente razonable, ¿no? Recopilaste algunos datos, los resultados no fueron concluyentes, así que ahora lo que quieres hacer es recolectar más datos hasta que los resultados sean concluyentes. ¿Qué tiene de malo eso?
Honestamente, no tiene nada de malo. Es una cosa razonable, sensata y racional de hacer. En la vida real, esto es exactamente lo que hace todo investigador. Desafortunadamente, la teoría de las pruebas de hipótesis nulas como la describí en el Capítulo 11 le prohíbe hacer esto. 263 La razón es que la teoría asume que el experimento está terminado y todos los datos están en. Y debido a que supone que el experimento ha terminado, sólo considera dos posibles decisiones. Si estás usando el umbral convencional p<.05, esas decisiones son:
| Resultado | Acción |
|---|---|
| p menos de .05 | Rechazar el nulo |
| p mayor que .05 | Conservar el valor nulo |
Lo que estás haciendo es agregar una tercera acción posible al problema de toma de decisiones. Específicamente, lo que estás haciendo es usar el valor p en sí mismo como una razón para justificar continuar con el experimento. Y como consecuencia has transformado el procedimiento de toma de decisiones en uno que se parece más a esto:
| Resultado | Acción |
|---|---|
| p menos de .05 | Detener el experimento y rechazar el nulo |
| p entre .05 y .1 | Continuar el experimento |
| p mayor que .1 | Detener el experimento y conservar el valor nulo |
La teoría “básica” de las pruebas de hipótesis nulas no está construida para manejar este tipo de cosas, ni en la forma que describí en el Capítulo 11. Si eres el tipo de persona que elegiría “recolectar más datos” en la vida real, implica que no estás tomando decisiones de acuerdo con las reglas de las pruebas de hipótesis nulas. Incluso si llegas a la misma decisión que la prueba de hipótesis, no estás siguiendo el proceso de decisión que implica, y es esta falta de seguir el proceso lo que está causando el problema. 264 Tus valores p son una mentira.
Peor aún, son una mentira de una manera peligrosa, porque todos son demasiado pequeños. Para darte una idea de lo malo que puede ser, considera el siguiente escenario (en el peor de los casos). Imagina que eres un investigador realmente súper entusiasta con un presupuesto ajustado que no prestó atención a mis advertencias anteriores. Diseñas un estudio comparando dos grupos. Desesperadamente quieres ver un resultado significativo en el nivel p<.05, pero realmente no quieres recopilar más datos de los que tienes que hacer (porque es caro). Para reducir costos, comienzas a recopilar datos, pero cada vez que llega una nueva observación haces una prueba t en tus datos. Si las pruebas t dicen p<.05 entonces detienes el experimento y reportas un resultado significativo. Si no, sigues recopilando datos. Sigues haciendo esto hasta llegar a tu límite de gasto predefinido para este experimento. Digamos que el límite entra en acción en N=1000 observaciones. Resulta que la verdad del asunto es que no hay ningún efecto real por encontrar: la hipótesis nula es cierta. Entonces, ¿cuál es la posibilidad de que llegues al final del experimento y (correctamente) concluyas que no hay ningún efecto? En un mundo ideal, la respuesta aquí debería ser del 95%. Después de todo, el objetivo del criterio p<.05 es controlar la tasa de error Tipo I al 5%, así que lo que esperaríamos es que solo haya un 5% de posibilidades de rechazar falsamente la hipótesis nula en esta situación. No obstante, no hay garantía de que sea cierto. Estás rompiendo las reglas: estás ejecutando pruebas repetidamente, “mirando” tus datos para ver si has obtenido un resultado significativo, y todas las apuestas están canceladas.
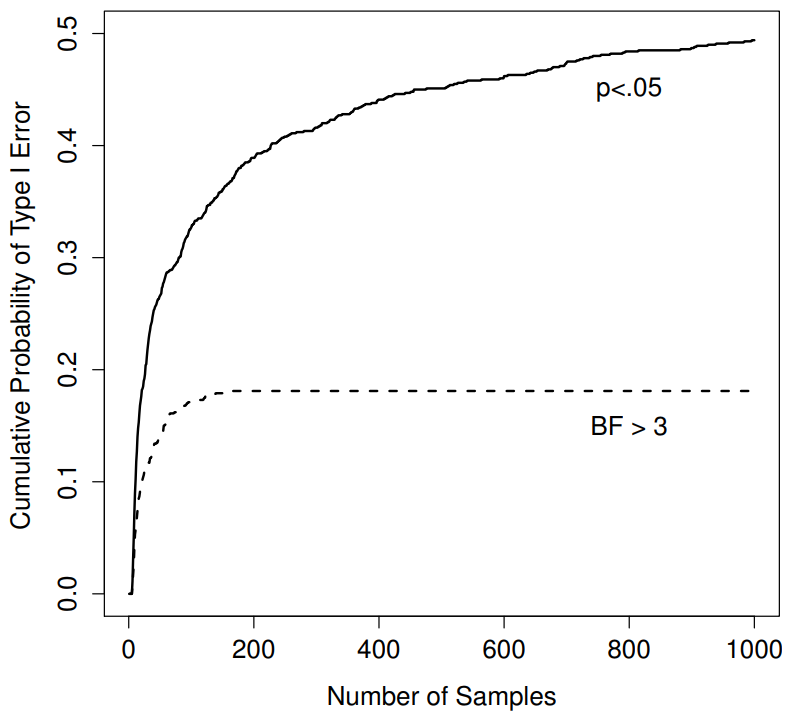
Figura 17.1: ¿Qué tan mal pueden salir las cosas si vuelves a ejecutar tus pruebas cada vez que llegan nuevos datos? Si eres frecuentista, la respuesta es “muy equivocada”.
Entonces, ¿qué tan malo es? La respuesta se muestra como la línea negra continua en la Figura 17.1, y es asombrosamente mala. Si echas un vistazo a tus datos después de cada observación, hay un 49% de posibilidades de que cometas un error de Tipo I. Eso es, um, bastante más grande que el 5% que se supone que es. A modo de comparación, imagina que habías utilizado la siguiente estrategia. Comience a recopilar datos. Cada vez que llega una observación, ejecuta una prueba t bayesiana (Sección 17.7 y observa el factor Bayes. Asumiré que Johnson (2013) tiene razón, y trataré un factor Bayes de 3:1 como aproximadamente equivalente a un valor p de .05. 265 En esta ocasión, nuestro investigador happy trigger utiliza el siguiente procedimiento: si el factor Bayes es 3:1 o más a favor del nulo, detener el experimento y retener el nulo. Si es 3:1 o más a favor de la alternativa, detenga el experimento y rechace el nulo. De lo contrario continuar las pruebas. Ahora, igual que la última vez, supongamos que la hipótesis nula es cierta. ¿Qué pasa? A medida que sucede, también ejecuté las simulaciones para este escenario, y los resultados se muestran como la línea discontinua en la Figura 17.1. Resulta que la tasa de error Tipo I es mucho más baja que la tasa de 49% que estábamos obteniendo al usar la prueba t ortodoxa.
De alguna manera, esto es notable. Todo el punto de la prueba de hipótesis nula ortodoxa es controlar la tasa de error Tipo I. Los métodos bayesianos en realidad no están diseñados para hacer esto en absoluto. Sin embargo, como resulta, ante un investigador “gatillo feliz” que sigue realizando pruebas de hipótesis a medida que entran los datos, el enfoque bayesiano es mucho más efectivo. Incluso el estándar 3:1, que la mayoría de los bayesianos consideraría inaceptablemente laxo, es mucho más seguro que la regla de p<.05.
¿realmente así de malo?
El ejemplo que di en la sección anterior es una situación bastante extrema. En la vida real, la gente no realiza pruebas de hipótesis cada vez que llega una nueva observación. Entonces no es justo decir que el umbral p<.05 “realmente” corresponde a una tasa de error de 49% Tipo I (es decir, p=.49). Pero el hecho es que si quieres que tus valores p sean honestos, entonces o tienes que cambiar a una forma completamente diferente de hacer pruebas de hipótesis, o debes hacer cumplir una regla estricta: no echar un vistazo. No se le permite utilizar los datos para decidir cuándo terminar el experimento. No se le permite mirar un valor p “límite” y decidir recopilar más datos. Ni siquiera se le permite cambiar su estrategia de análisis de datos después de mirar los datos. Se le exige estrictamente que siga estas reglas, de lo contrario los valores p que calcule no tendrán sentido.
Y sí, estas reglas son sorprendentemente estrictas. Como ejercicio de clase hace un par de años, pedí a los alumnos que pensaran en este escenario. Supongamos que empezaste a dirigir tu estudio con la intención de recolectar N=80 personas. Cuando comienza el estudio sigues las reglas, negándote a mirar los datos o ejecutar alguna prueba. Pero cuando llegas a N=50 tu fuerza de voluntad cede... y te das un vistazo. ¿Adivina qué? ¡Tienes un resultado significativo! Ahora, claro, ya sabes dijiste que seguirías ejecutando el estudio a un tamaño de muestra de N=80, pero ahora parece algo inútil, ¿verdad? El resultado es significativo con un tamaño de muestra de N=50, así que ¿no sería derrochador e ineficiente seguir recopilando datos? ¿No estás tentado a parar? ¿Sólo un poco? Bueno, ten en cuenta que si lo haces, tu tasa de error Tipo I en p<.05 acaba de dispararse al 8%. Cuando reportas p<.05 en tu trabajo, lo que realmente estás diciendo es p<.08. Así de malas pueden ser las consecuencias de “solo un vistazo”.
Ahora considere esto... la literatura científica está llena de pruebas t, ANOVAs, regresiones y pruebas de chi-cuadrado. Cuando escribí este libro no elegí estas pruebas arbitrariamente. La razón por la que estas cuatro herramientas aparecen en la mayoría de los textos estadísticos introductorios es que estas son las herramientas de pan y mantequilla de la ciencia. Ninguna de estas herramientas incluye una corrección para hacer frente al “asomamiento de datos”: todas asumen que no lo estás haciendo. Pero, ¿qué tan realista es esa suposición? En la vida real, ¿cuántas personas crees que han “echado un vistazo” a sus datos antes de que terminara el experimento y adaptaron su comportamiento posterior después de ver cómo se veían los datos? Excepto cuando el procedimiento de muestreo está fijado por una restricción externa, supongo que la respuesta es “la mayoría de la gente lo ha hecho”. Si eso ha sucedido, se puede inferir que los valores p reportados son incorrectos. Peor aún, porque no sabemos qué proceso de decisión siguieron realmente, no tenemos forma de saber cuáles deberían haber sido los valores p. No se puede calcular un valor p cuando no se conoce el procedimiento de toma de decisiones que utilizó el investigador. Y así el valor p reportado sigue siendo una mentira.
Ante todo lo anterior, ¿cuál es el mensaje para llevar a casa? No es que los métodos bayesianos sean infalibles. Si un investigador está decidido a hacer trampa, siempre puede hacerlo. La regla de Bayes no puede impedir que la gente mienta, ni tampoco puede impedirles de amañar un experimento. Ese no es mi punto aquí. Mi punto es el mismo que hice al principio del libro en la Sección 1.1: la razón por la que realizamos pruebas estadísticas es para protegernos de nosotros mismos. Y la razón por la que “echar un vistazo a los datos” es tal preocupación es que es tan tentador, incluso para investigadores honestos. Una teoría para la inferencia estadística tiene que reconocerlo. Sí, podrías intentar defender los valores p diciendo que es culpa del investigador por no utilizarlos correctamente. Pero en mi opinión eso pierde el punto. Una teoría de inferencia estadística tan completamente ingenua sobre los humanos que ni siquiera considera la posibilidad de que el investigador pueda mirar sus propios datos no es una teoría que valga la pena tener. En esencia, mi punto es el siguiente:
Las buenas leyes tienen su origen en la mala moral.
— Ambrosio Macrobio 266
Las buenas reglas para las pruebas estadísticas tienen que reconocer la fragilidad humana. Ninguno de nosotros está sin pecado. Ninguno de nosotros está más allá de la tentación. Un buen sistema de inferencia estadística aún debería funcionar incluso cuando es utilizado por humanos reales. Las pruebas ortodoxas de hipótesis nulas no. 267


