7.3: Modelo poblacional

Nuestro modelo de regresión se basa en una muestra de n observaciones bivariadas extraídas de una mayor población de mediciones.

$$\ hat y = b_0 +b_1x\]

Utilizamos las medias y desviaciones estándar de nuestros datos de muestra para calcular la pendiente (b 1) y la intersección y (b 0) con el fin de crear una línea de regresión ordinaria de mínimos cuadrados. Pero queremos describir la relación entre y y x en la población, no solo dentro de nuestros datos de muestra. Queremos construir un modelo poblacional. Ahora pensaremos en la línea de mínimos cuadrados calculada a partir de una muestra como estimación de la línea de regresión verdadera para la población.

Definición: El modelo poblacional

\(\mu_y = \beta_0 + \beta_1x\), donde\(\mu_y\) está la respuesta media poblacional,\(\beta_0\) es la intersección y, y\(beta_1\) es la pendiente para el modelo poblacional.

En nuestra población, podría haber muchas respuestas diferentes por un valor de x. En regresión lineal simple, el modelo asume que para cada valor de x los valores observados de la variable de respuesta y se distribuyen normalmente con una media que depende de x. Utilizamos μy para representar estas medias. También asumimos que todos estos medios se encuentran en una línea recta cuando se trazan contra x (una línea de medias).

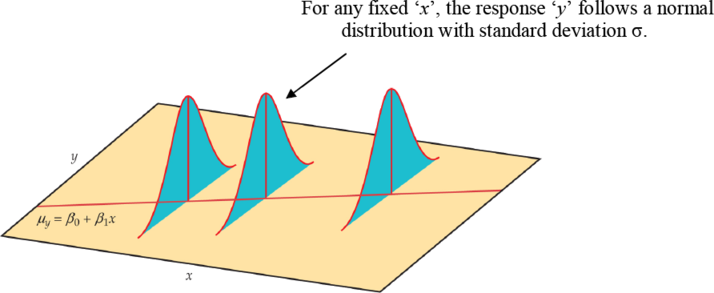
Figura 17. El modelo estadístico para regresión lineal; la respuesta media es una función de línea recta de la variable predictora.

Los datos de la muestra se ajustan entonces al modelo estadístico:

Datos = ajuste + residual

$$y_i = (\ beta_0 +\ beta_1x_i) +\ epsilon_i\]

donde los errores (εi) son independientes y normalmente distribuidos N (0, σ). La regresión lineal también asume la misma varianza de y (σ es la misma para todos los valores de x). Usamos ε (épsilon griego) para representar la parte residual del modelo estadístico. Una respuesta y es la suma de su media y desviación de probabilidad εde la media. Las desviaciones ε representan el “ruido” en los datos. Es decir, el ruido es la variación en y debido a otras causas que impiden que la observada (x, y) forme una línea perfectamente recta.

Los datos de muestra utilizados para la regresión son los valores observados de y y x. La respuesta y a una x dada es una variable aleatoria, y el modelo de regresión describe la media y desviación estándar de esta variable aleatoria y. La intersección β0, la pendiente β1 y la desviación estándar σ de y son los parámetros desconocidos del modelo de regresión y deben estimarse a partir de los datos de la muestra.

• El valor de y de la línea de regresión de mínimos cuadrados es realmente una predicción del valor medio de y (μy) para un valor dado de x.
• La línea de regresión de mínimos cuadrados (\(\hat y = b_0+b_1x\)) obtenida de los datos de la muestra es la mejor estimación de la línea de regresión poblacional verdadera
  (\(\mu_y = \beta_0 + \beta_1x\)).

y es una estimación imparcial para la respuesta media μy
b 0 es una estimación imparcial para la intercepción β0
b 1 es una estimación imparcial para la pendiente β1

Estimación de parámetros

Una vez que tenemos estimaciones de β0 y β1 (a partir de nuestros datos de muestra b 0 y b 1), la relación lineal determina las estimaciones de μy para todos los valores de x en nuestra población, no solo para los valores observados de x. Ahora queremos utilizar la línea de mínimos cuadrados como base para la inferencia sobre una población de la que se extrajo nuestra muestra.

Los supuestos del modelo nos dicen que b 0 y b1 normalmente se distribuyen con medias β0 y β1 con desviaciones estándar que pueden estimarse a partir de los datos. Los procedimientos de inferencia sobre la línea de regresión poblacional serán similares a los descritos en el capítulo anterior para las medias. Como siempre, es importante examinar los datos en busca de valores atípicos y observaciones influyentes.

Para ello, necesitamos estimar σ, el error estándar de regresión. Esta es la desviación estándar de los errores del modelo. Mide la variación de y sobre la línea de regresión poblacional. Usaremos los residuales para calcular este valor. Recuerde, el valor predicho de y (p) para una x específica es el punto en la línea de regresión. Es la estimación imparcial de la respuesta media (μy) para esa x. El residuo es:

residual = observado — predicho

$$\ épsilon_i = y_i —\ hat {y} = y_i - (b_0+b_1x)\]

El residual e i corresponde a la desviación del modelo\(\epsilon_i\) donde\(\sum \epsilon_i = 0\) con una media de 0. El error estándar de regresión s es una estimación imparcial de σ.

$$s=\ sqrt {\ dfrac {\ suma residual^2} {n-2}} =\ sqrt {\ dfrac {\ sum (y_i-\ hat {y_i}) ^2} {n-2}}\]

La cantidad s es la estimación del error estándar de regresión (σ) y a menudo\(s^2\) se denomina error cuadrático medio (MSE). Un pequeño valor de s sugiere que los valores observados de y caen cerca de la línea de regresión verdadera y la línea\(\hat y = b_0 +b_1x\) debe proporcionar estimaciones y predicciones precisas.

Intervalos de confianza y pruebas de significancia para los parámetros

En un capítulo anterior, construimos intervalos de confianza e hicimos pruebas de significancia para el parámetro poblacional μ (la media poblacional). Nos basamos en estadísticas de muestra como la media y desviación estándar para estimaciones puntuales, márgenes de errores y estadísticas de prueba. La inferencia para los parámetros poblacionales β0 (pendiente) y β1 (intersección y) es muy similar.

La inferencia para la pendiente y la intercepción se basan en la distribución normal utilizando las estimaciones b 0 y b 1. Las desviaciones estándar de estas estimaciones son múltiplos de σ, el error estándar de regresión poblacional. Recuerde, estimamos σ con s (la variabilidad de los datos sobre la línea de regresión). Debido a que usamos s, confiamos en la distribución t estudiantil con (n — 2) grados de libertad.

$$\ sigma_ {\ hat {\ beta_0}} =\ sigma\ sqrt {\ frac {1} {n} +\ dfrac {\ bar x ^2} {\ sum (x_i -\ bar x) ^2}}\]

El error estándar para la estimación de\(\beta_0\)

$$\ sigma_ {\ hat {\ beta_1}} =\ sigma\ sqrt {\ frac {1} {n} +\ dfrac {\ bar x ^2} {\ sum (x_i -\ bar x) ^2}}\]

El error estándar para la estimación de\(\beta_1\)

Podemos construir intervalos de confianza para la pendiente de regresión e interceptar de la misma manera que lo hicimos al estimar la media poblacional.

Un intervalo de confianza para\(\beta_0 : b_0 \pm t_{\alpha/2} SE_{b_0}\)

Un intervalo de confianza para\(\beta_1 : b_1 \pm t_{\alpha/2} SE_{b_1}\)

donde\(SE_{b_0}\) y\(SE_{b_1}\) son los errores estándar para la intersección y y la pendiente, respectivamente.

También podemos probar la hipótesis\(H_0: \beta_1 = 0\). Cuando sustituimos\(\beta_1 = 0\) en el modelo, el término x cae y nos quedamos con\(\mu_y = \beta_0\). Esto nos dice que la media de y NO varía con x. En otras palabras, no existe una relación de línea recta entre x e y y la regresión de y sobre x no tiene ningún valor para predecir y.

Prueba de hipótesis para\(\beta_1\)

\(H_0: \beta_1 =0\)

\(H_1: \beta_1 \ne 0\)

El estadístico de prueba es\(t = b_1 / SE_{b_1}\)

También podemos usar el estadístico F (MSR/MSE) en la tabla ANOVA de regresión*

*Recordemos que t2 = F

Así que vamos a juntar todo esto en un ejemplo.

Ejemplo\(\PageIndex{1}\):

El índice de integridad biótica (IBI) es una medida de la calidad del agua en los arroyos. Como gerente de los recursos naturales en esta región, debe monitorear, rastrear y predecir los cambios en la calidad del agua. Se desea crear un modelo de regresión lineal simple que le permita predecir cambios en IBI en área boscosa. La siguiente tabla muestra datos de una región forestal costera y da los datos para IBI y área boscosa en kilómetros cuadrados. Que el área forestal sea la variable predictora (x) e IBI sea la variable de respuesta (y).

Cuadro 1. Datos observados de integridad biótica y área forestal.

Solución

Comenzamos con una estadística descriptiva computacional y una gráfica de dispersión del IBI contra Área Forestal.

xï = 47.42; sx 27.37; yï = 58.80; sy = 21.38; r = 0.735

Figura 18. Gráfica de dispersión del IBI vs. Área Forestal.

Parece haber una relación lineal positiva entre las dos variables. El coeficiente de correlación lineal es r = 0.735. Esto indica una relación fuerte, positiva, lineal. En otras palabras, el área forestal es un buen predictor del IBI. Ahora vamos a crear un modelo de regresión lineal simple usando área de bosque para predecir IBI (respuesta).

Primero, calcularemos b 0 y b 1 usando las ecuaciones de atajo.

$$b_1 = r (\ frac {s_y} {s_x}) = 0.735 (\ frac {21.38} {27.37}) =0.574\]

$$b_0 =\ bar y -b_1\ barra x =58.80-0.574\ times 47.42=31.581\]

La ecuación de regresión es

$$\ hat y =31.58 + 0.574x$$.

Ahora usemos Minitab para calcular el modelo de regresión. La salida aparece a continuación.

Análisis de Regresión: IBI versus Área Forestal

La ecuación de regresión es IBI = 31.6 + 0.574 Área Forestal

Predictor	Coef	SE Coef	T	P
Constante	31.583	4.177	7.56	0.000
Área Forestal	0.57396	0.07648	7.50	0.000
S = 14.6505	R-Sq = 54.0%	R-Sq (adj) = 53.0%

Análisis de varianza
Fuente	DF	SS	MS	F	P
Regresión	1	12089	12089	56.32	0.000
Error residual	48	10303	215
Total	49	22392

Las estimaciones para β0 y β1 son 31.6 y 0.574, respectivamente. Podemos interpretar la intersección y para significar que cuando hay cero área boscosa, el IBI será igual a 31.6. Por cada kilómetro cuadrado adicional de área boscosa agregada, el IBI aumentará en 0.574 unidades.

El coeficiente de determinación, R2, es 54.0%. Esto significa que 54% de la variación en IBI se explica por este modelo. Aproximadamente el 46% de la variación en el IBI se debe a otros factores o variación aleatoria. Nos gustaría que R2 fuera lo más alto posible (valor máximo del 100%).

Las gráficas de probabilidad residual y normal no indican ningún problema.

Figura 19. Una gráfica de probabilidad residual y normal.

La estimación de σ, el error estándar de regresión, es s = 14.6505. Esta es una medida de la variación de los valores observados sobre la línea de regresión poblacional. Nos gustaría que este valor fuera lo más pequeño posible. El MSE es igual a 215. Recuerda, el\(\sqrt {MSE}=s\). Los errores estándar para los coeficientes son 4.177 para la intersección y y 0.07648 para la pendiente.

Sabemos que los valores b 0 = 31.6 y b 1 = 0.574 son estimaciones muestrales de los parámetros poblacionales verdaderos, pero desconocidos, β0 y β1. Podemos construir intervalos de confianza del 95% para estimar mejor estos parámetros. El valor crítico (tα/2) proviene de la distribución t estudiantil con (n — 2) grados de libertad. Nuestro tamaño de muestra es de 50 por lo que tendríamos 48 grados de libertad. El valor más cercano de la tabla es 2.009.

Intervalos de confianza del 95% para β0 y β1

$$b_0\ pm t_ {\ alpha/2} SE_ {b_0} = 31.6\ pm 2.009 (4.177) = (23.21, 39.99)\]

$$b_1\ pm t_ {\ alpha/2} SE_ {b_1} = 0.574\ pm 2.009 (0.07648) = (0.4204, 0.7277)\]

El siguiente paso es probar que la pendiente es significativamente diferente de cero usando un nivel de significancia del 5%.

H0: β1 =0

H1: β1 ≠ 0

$$t =\ frac {b_1} {SE_ {b_1}} =\ frac {0.574} {0.07648} = 7.50523\]

Tenemos 48 grados de libertad y el valor crítico más cercano de la distribución t estudiantil es 2.009. El estadístico de prueba es mayor que el valor crítico, por lo que rechazaremos la hipótesis nula. La pendiente es significativamente diferente de cero. Se encontró una relación estadísticamente significativa entre el Área Forestal y el IBI.

Los resultados de Minitab también reportan el estadístico de prueba y el valor p para esta prueba.

La ecuación de regresión es IBI = 31.6 + 0.574 Área Forestal
Predictor	Coef	SE Coef	T	P
Constante	31.583	4.177	7.56	0.000
Área Forestal	0.57396	0.07648	7.50	0.000
S = 14.6505	R-Sq = 54.0%	R-Sq (adj) = 53.0%

Análisis de varianza
Fuente	DF	SS	MS	F	P
Regresión	1	12089	12089	56.32	0.000
Error residual	48	10303	215
Total	49	22392

El estadístico de prueba t es 7.50 con un valor p asociado de 0.000. El valor p es menor que el nivel de significancia (5%) por lo que rechazaremos la hipótesis nula. La pendiente es significativamente diferente de cero. El mismo resultado se puede encontrar a partir del estadístico de prueba F de 56.32 (7.5052 = 56.32). El valor p es el mismo (0.000) que la conclusión.

Intervalo de confianza para\(\mu_y\)

Ahora que hemos creado un modelo de regresión construido sobre una relación significativa entre la variable predictora y la variable de respuesta, estamos listos para usar el modelo para

• estimar el valor promedio de y para un valor dado de x
• predecir un valor particular de y para un valor dado de x

Examinemos la primera opción. Los datos muestrales de n pares que se extrajeron de una población se utilizaron para calcular los coeficientes de regresión b 0 y b1 para nuestro modelo, y nos da el valor promedio de y para un valor específico de x a través de nuestro modelo poblacional\(\mu_y = \beta_0 + \beta_1x\)

. Por cada valor específico de x, hay un promedio y (μ y), que cae sobre la ecuación de línea recta (una línea de medias). Recuerde, que puede haber muchos valores observados diferentes de la y para una x particular, y se supone que estos valores tienen una distribución normal con una media igual a\(\beta_0 + \beta_1x\) y una varianza de σ2. Dado que los valores calculados de b 0 y b1 varían de una muestra a otra, cada nueva muestra puede producir una ecuación de regresión ligeramente diferente. Cada nuevo modelo se puede utilizar para estimar un valor de y para un valor de x. ¿Qué tan lejos estará nuestro estimador\(\hat y =b_0+b_1x\) de la verdadera población media para ese valor de x? Esto depende, como siempre, de la variabilidad en nuestro estimador, medida por el error estándar.

Se puede demostrar que el valor estimado de y cuando x = x 0 (algún valor especificado de x), es un estimador imparcial de la media poblacional, y que p se distribuye normalmente con un error estándar de

$SE_ {\ sombrero\ mu} = s\ sqrt {\ frac {1} {n} +\ frac {(x_0-\ bar x) ^2} {\ sum (x_i -\ bar x) ^2}}\]

Podemos construir un intervalo de confianza para estimar mejor este parámetro (μy) siguiendo el mismo procedimiento ilustrado anteriormente en este capítulo.

$$\ hat {\ mu_y}\ pm t_ {\ alpha/2} SE_ {\ sombrero\ mu}\]

donde el valor crítico tα/2 proviene de la tabla t estudiantil con (n — 2) grados de libertad.

El software estadístico, como Minitab, calculará los intervalos de confianza por usted. Usando los datos del ejemplo anterior, utilizaremos Minitab para calcular el intervalo de confianza del 95% para la respuesta media para un área boscosa promedio de 32 km.

Valores pronosticados para nuevas observaciones
Nuevo ajuste de Obs	SE Fit	95%	CI
1	49.9496	2.38400	(45.1562,54.7429)

Si muestreaste muchas áreas que promediaron 32 km. de superficie boscosa, tu estimación del IBI promedio sería de 45.1562 a 54.7429.

Puede repetir este proceso muchas veces para varios valores diferentes de x y trazar los intervalos de confianza para la respuesta media.

x	IC 95%
20	(37.13, 48.88)
40	(50.22, 58.86)
60	(61.43, 70.61)
80	(70.98, 84.02)
100	(79.88, 98.07)

Figura 20. Intervalos de confianza del 95% para la respuesta media.

Observe cómo varía el ancho del intervalo de confianza del 95% para los diferentes valores de x. Dado que el ancho del intervalo de confianza es más estrecho para los valores centrales de x, se deduce que μy se estima con mayor precisión para los valores de x en esta área. A medida que avanza hacia los límites extremos de los datos, el ancho de los intervalos aumenta, lo que indica que sería imprudente extrapolar más allá de los límites de los datos utilizados para crear este modelo.

Intervalos de predicción

¿Y si quieres predecir un valor particular de y cuándo\(x = x_0\)? O, ¿quizás quieres predecir la siguiente medición para un valor dado de x? Este problema difiere de construir un intervalo de confianza para\(\mu_y\). En lugar de construir un intervalo de confianza para estimar un parámetro de población, necesitamos construir un intervalo de predicción. Elegir predecir un valor particular de y incurre en algún error adicional en la predicción debido a la desviación de y de la línea de medias. Examine la figura a continuación. Se puede ver que el error en la predicción tiene dos componentes:

1. El error en el uso de la línea ajustada para estimar la línea de medias
2. El error causado por la desviación de y de la línea de medias, medido por\(\sigma^2\)

Figura 21. Ilustrando los dos componentes en el error de predicción.

La varianza de la diferencia entre y y\(\hat y\) es la suma de estas dos varianzas y forma la base para el error estándar de\((y-\hat y)\) utilizado para la predicción. La forma resultante de un intervalo de predicción es la siguiente:

$$\ hat y\ pm t_ {\ alpha/2} s\ sqrt {1+\ frac {1} {n} +\ frac {(x_0 -\ bar x) ^2} {\ sum (x_i -\ bar x) ^2}}\]

donde x 0 es el valor dado para la variable predictora, n es el número de observaciones, y\(t_{\alpha/2}\) es el valor crítico con (n — 2) grados de libertad.

El software, como Minitab, puede calcular los intervalos de predicción. Usando los datos del ejemplo anterior, utilizaremos Minitab para calcular el intervalo de predicción del 95% para el IBI de un área boscosa específica de 32 km.

Valores pronosticados para nuevas observaciones
Nuevo Obs	Fit	SE Fit	95% PI
1	49.9496	2.38400	(20.1053, 79.7939)

Puede repetir este proceso muchas veces para varios valores diferentes de x y trazar los intervalos de predicción para la respuesta media.

x	95% PI
20	(13.01, 73.11)
40	(24.77, 84.31)
60	(36.21, 95.83)
80	(47.33, 107.67)
100	(58.15, 119.81)

Observe que las bandas de intervalo de predicción son más anchas que las bandas de intervalo de confianza correspondientes, reflejando el hecho de que estamos predicando el valor de una variable aleatoria en lugar de estimar un parámetro de población. Esperaríamos que las predicciones para un valor individual fueran más variables que las estimaciones de un valor promedio.

Figura 22. Comparación de intervalos de confianza e predicción.

Transformaciones para Linealizar Relaciones de Datos

En muchas situaciones, la relación entre x e y es no lineal. Para simplificar el modelo subyacente, podemos transformar o convertir x o y o ambos para dar como resultado una relación más lineal. Hay muchas transformaciones comunes como logarítmica y recíproca. Incluir términos de orden superior en x también puede ayudar a linealizar la relación entre x e y. A continuación se muestran algunas formas comunes de diagramas de dispersión y posibles opciones para transformaciones. Sin embargo, la elección de la transformación suele ser más una cuestión de prueba y error que de reglas establecidas.

Figura 23. Ejemplos de posibles transformaciones para las variables x e y.

Ejemplo\(\PageIndex{2}\):

Un silvicultor necesita crear un modelo de regresión lineal simple para predecir el volumen del árbol usando diámetro a la altura del pecho (dbh) para arces azucareros. Recolecta dbh y volumen para 236 arces azucareros y parcelas volumen versus dbh. A continuación se muestra la gráfica de dispersión, el coeficiente de correlación y la salida de regresión de Minitab.

Figura 24. Gráfica de dispersión de volumen versus dbh.

El coeficiente de correlación lineal de Pearson es 0.894, lo que indica una relación lineal fuerte, positiva. Sin embargo, la gráfica de dispersión muestra una relación no lineal distinta.

Análisis de Regresión: volumen versus dbh

La ecuación de regresión es volume = — 51.1 + 7.15 dbh
Predictor	Coef	SE Coef	T	P
Constante	-51.097	3.271	-15.62	0.000
dbh	7.1500	0.2342	30.53	0.000
S = 19.5820	R-Sq = 79.9%		R-Sq (adj) = 79.8%

Análisis de varianza
Fuente	DF	SS	MS	F	P
Regresión	1	357397	357397	932.04	0.000
Error residual	234	89728	383
Total	235	447125

El R2 es 79.9% lo que indica un modelo bastante fuerte y la pendiente es significativamente diferente de cero. Sin embargo, tanto la gráfica residual como la gráfica de probabilidad normal residual indican serios problemas con este modelo. Una transformación puede ayudar a crear una relación más lineal entre volumen y dbh.

Figura 25. Gráficas de probabilidad residual y normal.

El volumen se transformó al logaritmo natural de volumen y se representó frente a dbh (ver diagrama de dispersión a continuación). Desafortunadamente, esto hizo poco para mejorar la linealidad de esta relación. Luego, el silvicultor tomó la transformación de bitácora natural de dbh. La gráfica de dispersión del logaritmo natural de volumen versus el logaritmo natural de dbh indicó una relación más lineal entre estas dos variables. El coeficiente de correlación lineal es 0.954.

Figura 26. Gráficas de dispersión de log natural de volumen versus dbh y log natural de volumen versus log natural de dbh.

El resultado del análisis de regresión de Minitab se da a continuación.

Análisis de Regresión: LnVol vs LnDBh

La ecuación de regresión es LnVol = — 2.86 + 2.44 LnDBh
Predictor	Coef	SE Coef	T	P
Constante	-2.8571	0.1253	-22.80	0.000
LnDBh	2.44383	0.05007	48.80	0.000
S = 0.327327	R-Sq = 91.1%	R-Sq (adj) = 91.0%

Análisis de varianza
Fuente	DF	SS	MS	F	P
Regresión	1	255.19	255.19	2381.78	0.000
Error residual	234	25.07	0.11
Total	235	280.26

Figura 27. Gráficas de probabilidad residual y normal.

El modelo que utiliza los valores transformados de volumen y dbh tiene una relación más lineal y un coeficiente de correlación más positivo. La pendiente es significativamente diferente de cero y el R2 ha aumentado de 79.9% a 91.1%. La gráfica residual muestra un patrón más aleatorio y la gráfica de probabilidad normal muestra alguna mejora.

Existen muchas combinaciones de transformación posibles para linealizar los datos. Cada situación es única y el usuario puede necesitar probar varias alternativas antes de seleccionar la mejor transformación para x o y o ambas.