5.3: Regresión curvilínea (no lineal)

Objetivos de aprendizaje

• Para usar regresión curvilínea cuando haya graficado dos variables de medición y desee ajustar una ecuación para una línea curva a los puntos de la gráfica.

A veces, cuando analizas datos con correlación y regresión lineal, notas que la relación entre la variable independiente (\(X\)) y la variable dependiente (\(Y\)) parece que sigue una línea curva, no una línea recta. En ese caso, la línea de regresión lineal no será muy buena para describir y predecir la relación, y el\(P\) valor puede no ser una prueba precisa de la hipótesis nula de que las variables no están asociadas.

Tienes tres opciones en esta situación. Si solo quieres saber si existe una asociación entre las dos variables, y no te interesa la línea que se ajuste a los puntos, puedes usar el\(P\) valor de regresión lineal y correlación. Esto podría ser aceptable si la línea es apenas ligeramente curvada; si tu pregunta biológica es “¿Más\(X\) causa más\(Y\)?” , puede que no le importe si una línea recta o una línea curva se ajusta\(Y\) mejor a la relación entre\(X\) y. Sin embargo, se verá extraño si usa regresión lineal y correlación en una relación que es fuertemente curvada, y algunas relaciones curvas, como una forma de U, pueden dar un\(P\) valor no significativo incluso cuando el ajuste a una curva en forma de U es bastante bueno. Y si quieres usar la ecuación de regresión para la predicción o te interesa la fuerza de la relación (\(r^2\)), definitivamente no debes usar regresión lineal y correlación cuando la relación es curva.

Hipótesis nulas

Una hipótesis nula que puedes probar al hacer regresión curvilínea es que no hay relación entre las\(Y\) variables\(X\) y; en otras palabras, que conocer el valor de no te\(X\) ayudaría a predecir el valor de\(Y\). Esto es análogo a probar la hipótesis nula de que la pendiente se encuentra\(0\) en una regresión lineal.

Se mide el ajuste de una ecuación a los datos con\(R^2\), análogo a la\(r^2\) de regresión lineal. A medida que agrega más parámetros a una ecuación, siempre se ajustará mejor a los datos; por ejemplo, una ecuación cuadrática de la forma

\[\hat{Y}=a+b_1X+b_2X^2\]

siempre estará más cerca de los puntos que una ecuación lineal de la forma

\[\hat{Y}=a+b_1X\]

por lo que la ecuación cuadrática siempre tendrá una\(R^2\) mayor que la lineal. Una ecuación cúbica siempre tendrá una\(R^2\) mayor que la cuadrática, y así sucesivamente. La segunda hipótesis nula de regresión curvilínea es que el incremento en\(R^2\) es tan grande como cabría esperar por casualidad.

Tu tercera opción es la regresión curvilínea: encontrar una ecuación que produzca una línea curva que se ajuste a tus puntos. Hay muchas ecuaciones que producirán líneas curvas, incluyendo exponencial (involucrando\(b^x\), donde\(b\) es una constante), potencia (involucrando\(X^b\)), logarítmica (involucrando\(\log (X)\)) y trigonométrica (involucrando seno, coseno, u otras funciones trigonométricas). Para cualquier forma particular de ecuación que involucre tales términos, puede encontrar la ecuación para la línea curva que mejor se ajuste a los puntos de datos, y comparar el ajuste de la ecuación más complicada con el de una ecuación más simple (como la ecuación para una línea recta).

Aquí utilizaré la regresión polinómica como un ejemplo de regresión curvilínea, luego mencionaré brevemente algunas otras ecuaciones que se usan comúnmente en biología. Una ecuación polinómica es cualquier ecuación que haya\(X\) elevado a potencias enteras como\(X^2\) y\(X^3\). Una ecuación polinómica es una ecuación cuadrática, que tiene la forma

\[\hat{Y}=a+b_1X+b_2X^2\]

donde\(a\) está el\(y\) —intercept\(b_1\) y y\(b_2\) son constantes. Produce una parábola. Una ecuación cúbica tiene la forma

\[\hat{Y}=a+b_1X+b_2X^2+b_3X^3\]

y produce una curva en forma de S, mientras que una ecuación cuártica tiene la forma

\[\hat{Y}=a+b_1X+b_2X^2+b_3X^3+b_4X^4\]

y puede producir\(M\) o dar\(W\) forma a curvas. Puedes encajar ecuaciones polinómicas de orden superior, pero es muy poco probable que quieras usar algo más que el cúbico en biología.

Supuestos

Si estás probando la hipótesis nula de que no hay asociación entre las dos variables de medición, la regresión curvilínea supone que la\(Y\) variable está normalmente distribuida y homoscedástica para cada valor de\(X\). Dado que la regresión lineal es robusta a estos supuestos (violarlos no aumenta mucho las probabilidades de un falso positivo), supongo que la regresión curvilínea puede no ser sensible a violaciones de la normalidad u homocedasticidad tampoco. No estoy al tanto de ningún estudio de simulación sobre esto, sin embargo.

La regresión curvilínea también asume que los puntos de datos son independientes, al igual que lo hace la regresión lineal. No se debe probar la hipótesis nula de no asociación para datos no independientes, como muchas series de tiempo. Sin embargo, hay muchos experimentos en los que ya sabes que hay una asociación entre las\(Y\) variables\(X\) y, y tu objetivo no es la prueba de hipótesis, sino estimar la ecuación que se ajuste a la línea. Por ejemplo, una práctica común en microbiología es cultivar bacterias en un medio con abundantes recursos, medir la abundancia de las bacterias en diferentes momentos y ajustar una ecuación exponencial a la curva de crecimiento. La cantidad de bacterias después de 30 minutos no es independiente de la cantidad de bacterias después de\(20\) minutos; si hay más a los\(20\) minutos, seguramente habrá más a los\(30\) minutos. Sin embargo, el objetivo de tal experimento no sería ver si las bacterias aumentan en abundancia con el tiempo (duh, claro que sí); el objetivo sería estimar qué tan rápido crecen, ajustando una ecuación exponencial a los datos. Para ello, no importa que los puntos de datos no sean independientes.

Así como la regresión lineal supone que la relación a la que está ajustando una línea recta es lineal, la regresión curvilínea asume que está ajustando el tipo de curva apropiado a sus datos. Si estás ajustando una ecuación cuadrática, la suposición es que tus datos son cuadráticos; si estás ajustando una curva exponencial, la suposición es que tus datos son exponenciales. Violar esta suposición, ajustar una ecuación cuadrática a una curva exponencial, por ejemplo, puede darte una ecuación que no se ajusta muy bien a tus datos.

En algunos casos, puede elegir el tipo de ecuación a utilizar en base a una comprensión teórica de la biología de su experimento. Si estás cultivando bacterias por un corto periodo de tiempo con abundantes recursos, esperas que su crecimiento siga una curva exponencial; si crecen lo suficiente para que los recursos empiecen a limitar su crecimiento, esperas que el crecimiento se ajuste a una curva logística. Otras veces, puede que no haya una razón teórica clara para una ecuación en particular, pero otras personas en tu campo han encontrado una que se ajusta bien a tu tipo de datos. Y en otros casos, solo necesitas probar una variedad de ecuaciones hasta encontrar una que funcione bien para tus datos.

Cómo funciona la prueba

En la regresión polinómica, se agregan diferentes potencias de la\(X\) variable (\(X,\; X^2,\; X^3…\)) a una ecuación para ver si aumentan\(R^2\) significativamente la. Primero se realiza una regresión lineal, ajustando una ecuación de la forma\(\hat{Y}=a+b_1X\) a los datos. Entonces se ajusta una ecuación de la forma\ hat {Y} =A+B_1x+B_2x^2\), que produce una parábola, a los datos. El siempre\(R^2\) aumentará cuando se agrega un término de orden superior, pero la cuestión es si el aumento en\(R^2\) es significativamente mayor de lo esperado debido al azar. A continuación, se ajusta una ecuación de la forma\(\hat{Y}=a+b_1X+b_2X^2+b_3X^3\), que produce una línea en forma de S, y se prueba el aumento en\(R^2\). Se puede seguir haciendo esto hasta que agregar otro término no aumente\(R^2\) significativamente, aunque en la mayoría de los casos es difícil imaginar un significado biológico para exponentes mayores que\(3\). Una vez que encuentre la ecuación que mejor se ajuste, la prueba para ver si se ajusta a los datos significativamente mejor que una ecuación de la forma\(Y=a\); en otras palabras, una línea horizontal.

A pesar de que el procedimiento habitual es probar primero la regresión lineal, luego la cuadrática, luego la cúbica, no es necesario detenerse si una de estas no es significativa. Por ejemplo, si la gráfica se ve en forma de U, la regresión lineal puede no ser significativa, pero la cuadrática podría serlo.

Ejemplo 1

Fernández-Juricic et al. (2003) examinaron el efecto de la perturbación humana en la anidación de gorriones (Passer domesticus). Contaron gorriones reproductores por hectárea en\(18\) parques de Madrid, España, y también contaron el número de personas por minuto caminando por cada parque (ambas variables de medición).

Fig. 5.3.1 Gráfico de abundancia de gorrión vs. perturbación humana con línea de regresión lineal.

La regresión lineal no es significativa (\(r^2=0.174,\; 16 d.f.,\; P=0.08\)).

Fig. 5.3.2 Gráfico de abundancia de gorrión vs. perturbación humana con línea de regresión cuadrática.

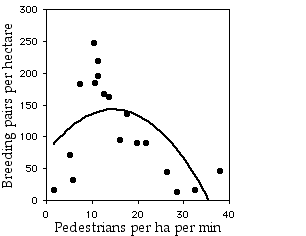
La regresión cuadrática es significativa (\(R^2=0.372,\; 15 d.f.,\; P=0.03\)), y es significativamente mejor que la regresión lineal (\(P=0.03\)). Esto parece biológicamente plausible; los datos sugieren que hay algún nivel intermedio de tráfico humano que es mejor para los gorriones de casa. Quizás áreas con demasiados humanos ahuyentan a los gorriones, mientras que las áreas con muy pocos humanos favorecen a otras aves que superan a los gorriones por anidar o algo así.

Fig. 5.3.3 Gráfico de abundancia de gorrión vs. perturbación humana con línea de regresión cúbica.

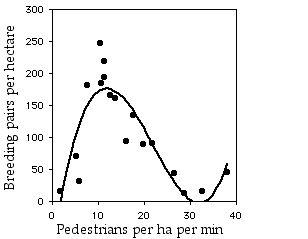
La gráfica cúbica es significativa (\(R^2=0.765,\; 14 d.f.,\; P=0.0001\)), y el incremento\(R^2\) entre la ecuación cúbica y la cuadrática es altamente significativo (\(P=1\times 10^{-5}\)). La ecuación cúbica es

\[Ŷ=−87.765+50.601X−2.916X^2+0.0443X^3.\]

La ecuación cuártica no se ajusta significativamente mejor que la ecuación cúbica (\(P=0.80\)). Aunque la ecuación cúbica se ajusta significativamente mejor que la cuadrática, es más difícil imaginar una explicación biológica plausible para esto. Me gustaría ver más muestras de áreas con más de\(35\) personas por hectárea por minuto antes de aceptar que la abundancia de gorriones realmente comienza a aumentar nuevamente por encima de ese nivel de tránsito peatonal.

Ejemplo 2

Ashton et al. (2007) midieron la longitud del caparazón (en mm) de las tortugas gopher\(18\) hembra (Gopherus polyphemus) en Okeeheelee County Park, Florida, y las radiografiaron para contar el número de huevos en cada una. Los datos se muestran a continuación en el ejemplo de SAS. La regresión lineal no es significativa (\(r^2=0.015,\; 16 d.f.,\; P=0.63\)), pero la cuadrática es significativa (\(R^2=0.43,\; 15 d.f.,\; P=0.014\)). El incremento\(R^2\) de lineal a cuadrático es significativo (\(P= 0.001\)). La ecuación cuadrática que mejor se ajusta es\(\hat{Y}=-899.9+5.857X-0.009425X^2\). Agregar los términos cúbicos y cuárticos no aumenta significativamente el\(R^2\).

Fig. 5.3.4 Radiografía de una tortuga, mostrando huevos.

Fig. 5.3.5 Gráfico de tamaño nidada (número de huevos) vs. longitud de caparazón, con línea cuadrática de mejor ajuste.

La primera parte de la gráfica no es sorprendente; es fácil imaginar por qué las tortugas más grandes tendrían más huevos. La disminución en el número de huevos por encima de la longitud del\(310 mm\) caparazón es el resultado interesante; sugiere que la producción de huevos disminuye en estas tortugas a medida que envejecen y crecen.

Graficando los resultados

Como se muestra arriba, graficas una regresión curvilínea de la misma manera que lo harías con una regresión lineal, un scattergraph con la variable independiente en el\(X\) eje y la variable dependiente en el\(Y\) eje. En general, no se debe mostrar la línea de regresión para valores fuera del rango de\(X\) valores observados, ya que la extrapolación con regresión polinómica es incluso más probable que la regresión lineal para producir resultados ridículos. Por ejemplo, extrapolar la ecuación cuadrática que relaciona la longitud del caparazón de tortuga y el número de huevos predice que las tortugas con longitud de caparazón menor\(279 mm\) o mayor que\(343 mm\) tendrían números negativos de huevos.

Pruebas similares

Antes de realizar una regresión curvilínea, debe probar diferentes transformaciones cuando se enfrenta a una relación obviamente curva entre una\(X\) y una\(Y\) variable. Una ecuación lineal que relaciona variables transformadas es más simple y elegante que una ecuación curvilínea que relaciona variables no transformadas. También debes recordarte tu razón para hacer una regresión. Si tu propósito es la predicción de valores desconocidos de\(Y\) correspondientes a valores conocidos de\(X\), entonces necesitas una ecuación que se ajuste bien a los puntos de datos, y una regresión polinómica puede ser apropiada si las transformaciones no funcionan. Sin embargo, si su propósito es probar la hipótesis nula de que no hay relación entre\(X\) y\(Y\), y una regresión lineal da un resultado significativo, es posible que desee seguir con la regresión lineal incluso si curvilínea da un ajuste significativamente mejor. Usar una técnica menos familiar que produzca una ecuación más complicada puede hacer que tus lectores sospechen un poco de tus resultados; pueden sentir que fuiste a buscar una prueba estadística que respaldara tu hipótesis, especialmente si no hay una razón biológica obvia para una ecuación con términos que contiene exponentes.

La correlación de rangos de Spearman es una prueba no paramétrica de la asociación entre dos variables. Funcionará bien si hay un aumento o disminución constante en a\(Y\) medida que\(X\) aumenta, pero no si\(Y\) sube y luego baja.

La regresión polinómica es una forma de regresión múltiple. En regresión múltiple, hay una variable dependiente (\(Y\)) y múltiples variables independientes (\(X\)), y las\(X\) variables (\(X_1,\; X_2,\; X_3...\)) se agregan a la ecuación para ver si aumentan la\(R^2\) significativamente. En regresión polinomial, las “variables” independientes son\(X^1,\; X^2,\; X^3\) justas, etc.

Cómo hacer la prueba

Hoja de Cálculo

He preparado una hoja de cálculo polyreg.xls que te ayudará a realizar una regresión polinómica. Prueba ecuaciones hasta cuárticas, y manejará hasta\(1000\) observaciones.

Páginas web

Hay una página web muy poderosa que se ajustará a casi cualquier ecuación que se te ocurra a tus datos (no solo polinomio).

R

El\(R\) compañero de Salvatore Mangiafico tiene programas R de muestra para regresión polinómica y otras formas de regresión que no discuto aquí (regresión B-spline y otras formas de regresión no lineal).

SAS

Para hacer regresión polinómica en SAS, se crea un conjunto de datos que contiene el cuadrado de la variable independiente, el cubo, etc. A continuación, se utiliza PROC REG para los modelos que contienen las variables de orden superior. Es posible hacer esto como una regresión múltiple, pero creo que es menos confuso usar múltiples declaraciones de modelo, agregando un término a cada modelo. No parece haber una manera fácil de probar la significación del\(R^2\) aumento de SAS, así que tendrás que hacerlo a mano. Si\(R_{i}^{2}\) es el\(R^2\) para el\(i_{th}\) orden, y\(R_{j}^{2}\) es el\(R^2\) para el siguiente orden superior, y\(d.f._j\) es los grados de libertad para la ecuación de orden superior, el\(F\) -estadístico es\(d.f._j\times (R_{j}^{2}-R_{i}^{2})/(1-R_{j}^{2})\). Tiene\(j\) grados de libertad en el numerador y\(d.f._j=n-j-1\) grados de libertad en el denominador.

Aquí hay un ejemplo, usando los datos sobre la longitud del caparazón de tortuga y el tamaño del embrague de Ashton et al. (2007).

Tortugas DATA;
ENTRADA longitud embrague;

longitud2=largo*largo;
longitud3=largo*largo*largo; longitud4=largo*largo*largo*largo;
DATALINES;
284 3
290 2
290 7
290 7
298 11
299 12
302 10
306 8
306 8
309 9
310 10
311 13
317 7
317 9
320 6
323 13
334 2
334 8
;
PROC REG DATA=TORTUGAS;
EMBRAGADO MODELO=longitud;
EMBRAGADO MODELO=longitud longitud2;
MODELO embraguza=longitud longitud2 largo3;
CORRIR;
En la salida, primero busque los\(R^2\) valores bajo cada modelo:

El
modelo de procedimiento REG: MODEL1 Variable
dependiente: embrague
.
.
.
Raíz MSE 3.41094 R-cuadrado 0.0148 lineal R-sq Media
dependiente 8.05556 Adj R-Sq -0.0468
Coeff Var 42.34268
.
.
.
El
modelo de procedimiento REG: MODEL2 Variable
dependiente: embrague
.
.
.
Raíz MSE 2.67050 R-Square 0.4338 cuadrático R-sq Media
Dependiente 8.05556 Adj R-Sq 0.3583
Coeff Var 33.15104

Para este ejemplo,\(n=18\). El\(F\) -estadístico para el incremento\(R^2\) de lineal a cuadrático es\(15\times \frac{0.4338-0.0148}{1-0.4338}=11.10\) con\(d.f.=2,\; 15\). Usando una hoja de cálculo (enter =FDIST (11.10, 2, 15)), esto da un\(P\) valor de\(0.0011\). Entonces la ecuación cuadrática se ajusta a los datos significativamente mejor que la ecuación lineal.

Una vez que hayas descubierto qué ecuación es la mejor (la cuadrática, para nuestro ejemplo, ya que las ecuaciones cúbica y cuártica no aumentan significativamente la\(R^2\)), busca los parámetros en la salida:

Parámetro Estimaciones Parámetro
Variable Estándar DF Estimación Error t Valor Pr > |t|

Intercepción 1 -899.93459 270.29576 -3.33 0.0046
longitud 1 5. 85716 1.75010 3.35 0.0044
largo2 1 -0.00942 0.00283 -3.33 0.0045

Esto te dice que la ecuación para la curva cuadrática que mejor se ajusta es\(\hat{Y}=-899.9+5.857X-0.009425X^2\).

Referencias

1. Radiografía de una tortuga de The Tortoise Shop.
2. Ashton, K.G., R.L. Burke, y J.N. Layne. 2007. Variación geográfica en el cuerpo y tamaño de nidada de tortugas gopher. Copeia 2007:355-363.
3. Fernández-Juricic, E., A. Sallent, R. Sanz, e I. Rodríguez-Prieto. 2003. Prueba de la hipótesis de riesgo-perturbación en un paisaje fragmentado: respuestas no lineales de gorriones de casa a los humanos. Cóndor 105:316-326.