4.2: Encontrar probabilidades con la curva normal
- Page ID
- 150266
Si queremos encontrar la probabilidad de que una puntuación caiga en un cierto rango, por ejemplo, entre 3 y 7, o más de 12, podemos usar la normal para determinar esa probabilidad. Nuestra capacidad para hacer esa determinación se basa en algunas características conocidas en la curva normal. Sabemos que para todas las curvas normales 68.26% de todas las puntuaciones se encuentran dentro de una desviación estándar de la media, que 95.44% cae dentro de dos desviaciones estándar, y que 99.72% caen dentro de tres desviaciones estándar. (La distribución normal se trata de manera más formal en el siguiente capítulo.) Entonces, sabemos que algo que es tres o más desviaciones estándar por encima de la media es bastante raro. La figura\(\PageIndex{1}\) ilustra las probabilidades asociadas a la curva normal. 7
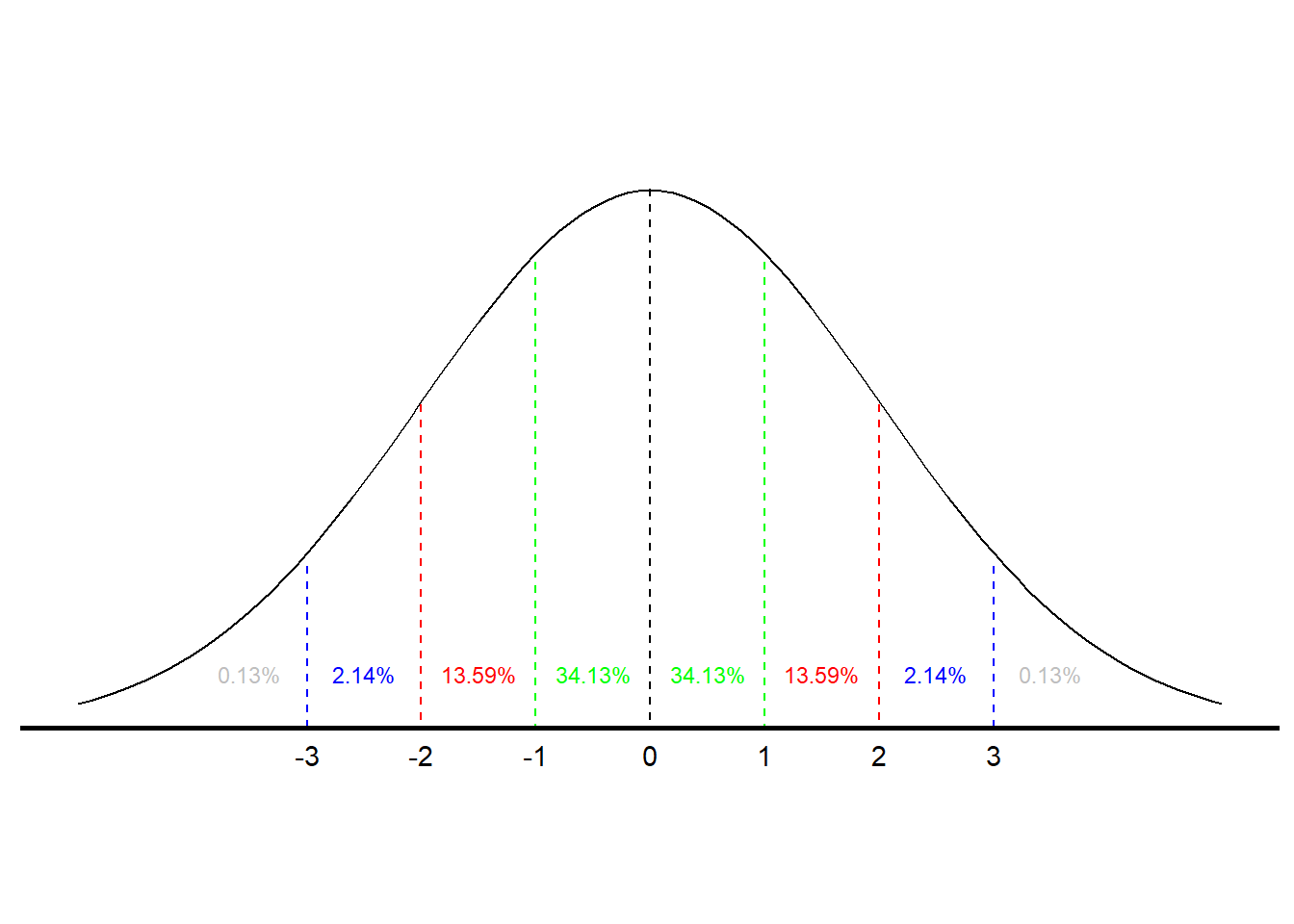
Según la Figura\(\PageIndex{1}\), existe una probabilidad de .3413 de que una observación caiga entre la media y una desviación estándar por encima de la media y, por lo tanto, una probabilidad de .6826 de que una puntuación caiga dentro de (+/−) (+/−) una desviación estándar de la media. También hay una probabilidad de .8413 de que una puntuación sea una desviación estándar por encima de la media o menos (.5 probabilidad de que una puntuación caiga por debajo de la media y una probabilidad de .3413 de que una puntuación caiga entre la media y una desviación estándar por encima de ella). (Utilizando el lenguaje que aprendimos en el Capítulo 3, otra forma de articular ese hallazgo es decir que una puntuación una desviación estándar por encima de la media está en el percentil 84.) También hay una probabilidad de .1587 de que una puntuación sea una desviación estándar por encima de la media o superior (1.0−.8413) (1.0−.8413).
Las pruebas de inteligencia tienen una media de 100 y una desviación estándar de 15. Alguien con un coeficiente intelectual de 130, entonces, está dos desviaciones estándar por encima de la media, es decir, obtiene una puntuación superior al 97.72% de la población. Sin embargo, supongamos que su coeficiente intelectual es de 140. El uso de Figure solo nos\(\PageIndex{1}\) permitiría aproximar qué tan alto es ese puntaje. Para conocer con mayor precisión, tenemos que averiguar cuántas desviaciones estándar por encima de la media 140 es y luego ir a una tabla de curvas normales más precisa.
Para saber cuántas desviaciones estándar de la media es una observación, calculamos una puntuación estandarizada o Z. La fórmula para convertir una puntuación sin procesar en una puntuación Z es:
Z=X−μσ (4.4) (4.4) Z=X−μσ
En este caso, la puntuación ZZ es 140−100/15140−100/15 o 2.672.67. Al observar la fórmula, se puede ver que una puntuación Z de cero pone esa puntuación en la media; una puntuación ZZ de uno es una desviación estándar por encima de la media, y una puntuación ZZ de 2.672.67 es 2.672.67 desviaciones estándar por encima de la media.
El siguiente paso es ir a una tabla de curvas normales para interpretar esa puntuación Z. El cuadro @ref (fig: Curva_Normal) al final del capítulo contiene dicha tabla. Para usar la tabla se combinan filas y columnas para encontrar una puntuación de 2.67. Donde cruzan vemos el valor .4962. Ese valor significa que hay una probabilidad de puntuación de .4962 entre la media y una puntuación ZZ de 2.67. Dado que hay una probabilidad .5 de puntuar por debajo de la media sumar los dos valores juntos da una probabilidad de .9962 de encontrar un coeficiente intelectual de 140 o inferior o una probabilidad de .0038 de que alguien tenga un coeficiente intelectual de 140 o mejor.
Probabilidades de Bernoulli
Podemos utilizar un cálculo conocido como Proceso de Bernoulli para determinar la probabilidad de un cierto número de éxitos en un número determinado de ensayos. Por ejemplo, si quieres saber la probabilidad de obtener exactamente tres cabezas al voltear una moneda cuatro veces, puedes usar el cálculo de Bernoulli. Para realizar el cálculo es necesario determinar el número de ensayos (n) (n), el número de éxitos que te importan (k) (k), la probabilidad de éxito en un solo ensayo (p) (p) y la probabilidad (q) (q) de no éxito (1−p (1−p o q) q). La fórmula operativa es:
(n! ¡k! (n−k)!) *pk*qn−k (n! ¡k! (n−k)!) *pk*qn−k
El símbolo n! n! es n factorial” o n∗ (n−1) ∗ (n−2) n∗ (n−1) ∗ (n−2) ∗ (n−2)... *1*1. Entonces, si quieres saber la probabilidad de obtener tres cabezas en cuatro volteos de una moneda, n=4n=4, k=3k=3, p=.5p=.5, y q=.5q=.5:
(¡4! ¡3! (4−3)!) *.53*.54−3=.25 (4! ¡3! (4−3)!) *.53*.54−3=.25
El proceso de Bernoulli sólo se puede utilizar cuando tanto n*pn*p como n*qn*q son mayores a diez. También es de mayor utilidad cuando te interesan exactamente los éxitos kk. Si quieres saber la probabilidad de kk o más, o kk o menos éxitos, es más fácil usar la curva normal. Bernoulli aún podría usarse si tus datos son discretos, pero tendrías que hacer cálculos repetidos.


