5.2: La distribución normal
- Page ID
- 150178
Figura\(\PageIndex{1}\): La distribución normal
Tenga en cuenta que las colas van a ±∞ ±∞. Además, la densidad de una distribución sobre el rango de x es la clave para la prueba de hipótesis Con una distribución normal, ∼ 68% ∼ 68% de las observaciones caerán dentro de 11 desviaciones estándar de la media, ∼ 95% ~ 95% caerán dentro de 2 desviaciones estándar, y ∼ 99.7% ∼ 99.7% dentro de 3 desviaciones estándar. Esto se ilustra en las Figuras 5.2, 5.3, 5.4.
Figura\(\PageIndex{1}\): La distribución normal
Tenga en cuenta que las colas van a ±∞ ±∞. Además, la densidad de una distribución sobre el rango de x es la clave para la prueba de hipótesis Con una distribución normal, ∼ 68% ∼ 68% de las observaciones caerán dentro de 11 desviaciones estándar de la media, ∼ 95% ~ 95% caerán dentro de 2 desviaciones estándar, y ∼ 99.7% ∼ 99.7% dentro de 3 desviaciones estándar. Esto se ilustra en las Figuras 5.2, 5.3, 5.4.
Para fines de inferencia estadística, la distribución normal es uno de los tipos más importantes de distribuciones de probabilidad. Forma la base de muchos de los supuestos necesarios para realizar el análisis cuantitativo de datos, y es la base para una amplia gama de pruebas de hipótesis. Una distribución normal estandarizada tiene una media, μμ, de 00 y una desviación estándar (s.d.), σσ, de 11. La distribución de una variable de resultado, YY, se puede describir:
Y~N (μY, σ2Y) (5.1) (5.1) Y~N (μY, σY2)
Donde ~∼ significa “distribuido como”, NN indica la distribución normal, y la media μYμY y varianza σ2Yσy2 son los parámetros. La función de probabilidad de la distribución normal se expresa a continuación:
La Función de Densidad de Probabilidad Normal: La función de densidad de probabilidad (PDF) de una distribución normal con media μμ y desviación estándar σσ:
$f(x) = \frac{1}{\sigma \sqrt{2 \pi}} e^{-(x-\mu)^{2}/2\sigma^{2}}$La Función de Densidad de Probabilidad Normal Estándar: El PDF normal estándar tiene un μ=0μ=0 y σ=1σ=1
$f(x) = \frac{1}{\sqrt{2 \pi}}e^{-x^{2}/2}$
Usando el PDF normal estándar, podemos trazar una distribución normal en R.
x <- seq(-4,4,length=200)
y <- 1/sqrt(2*pi)*exp(-x^2/2)
plot(x,y, type="l", lwd=2)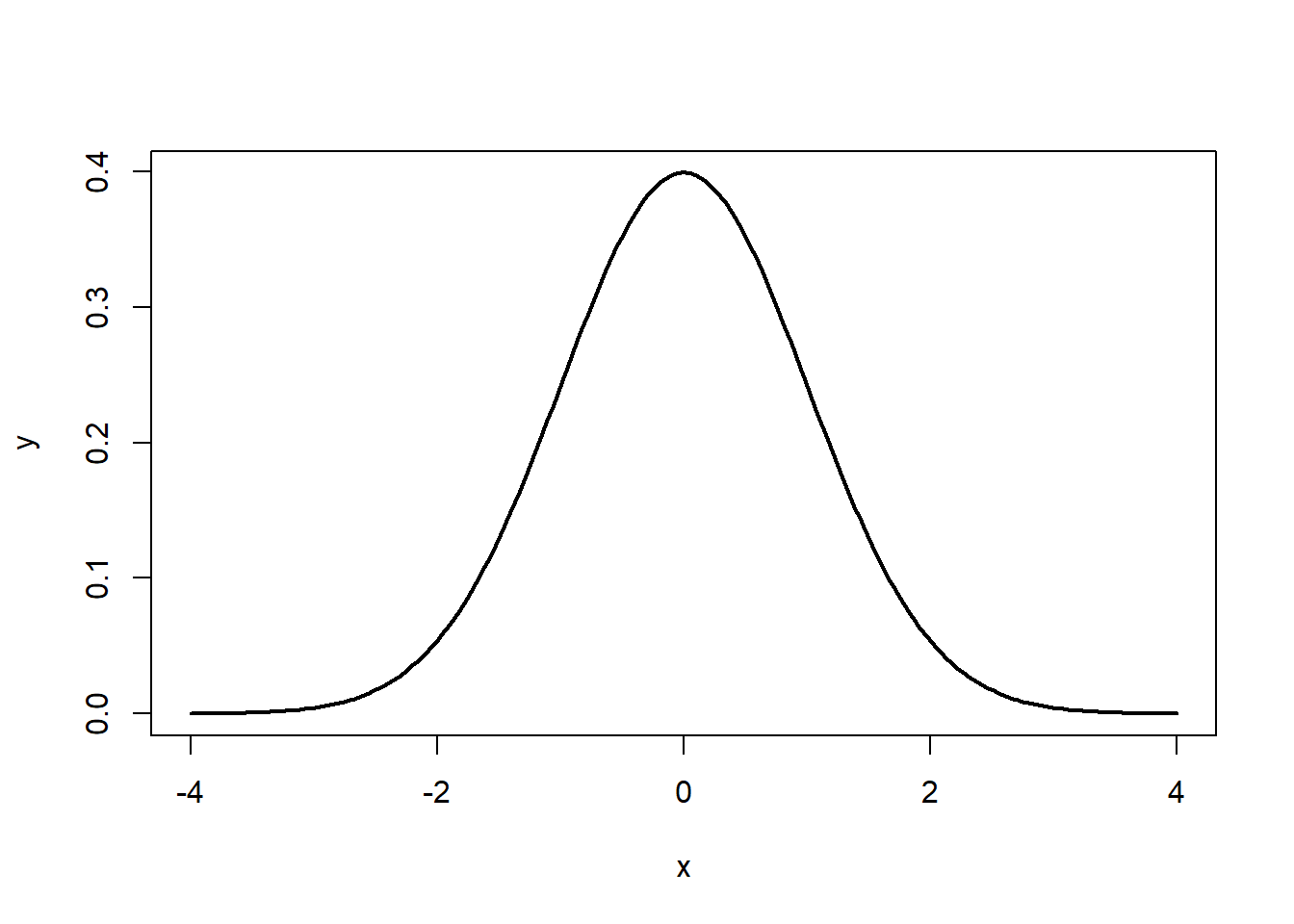
Tenga en cuenta que las colas van a ±∞ ±∞. Además, la densidad de una distribución sobre el rango de x es la clave para la prueba de hipótesis Con una distribución normal, ∼ 68% ∼ 68% de las observaciones caerán dentro de 11 desviaciones estándar de la media, ∼ 95% ~ 95% caerán dentro de 2 desviaciones estándar, y ∼ 99.7% ∼ 99.7% dentro de 3 desviaciones estándar. Esto se ilustra en las Figuras 5.2, 5.3, 5.4.
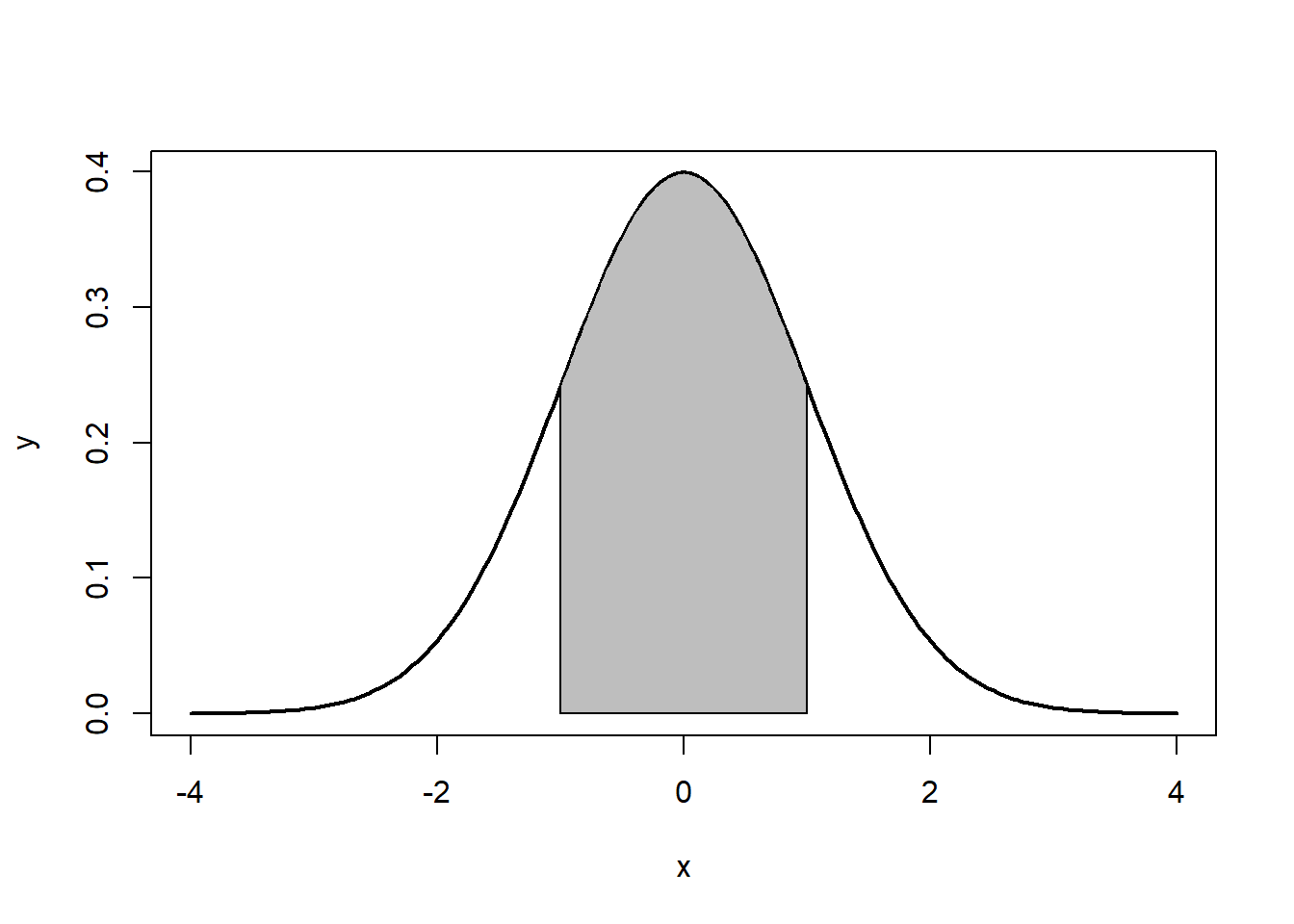
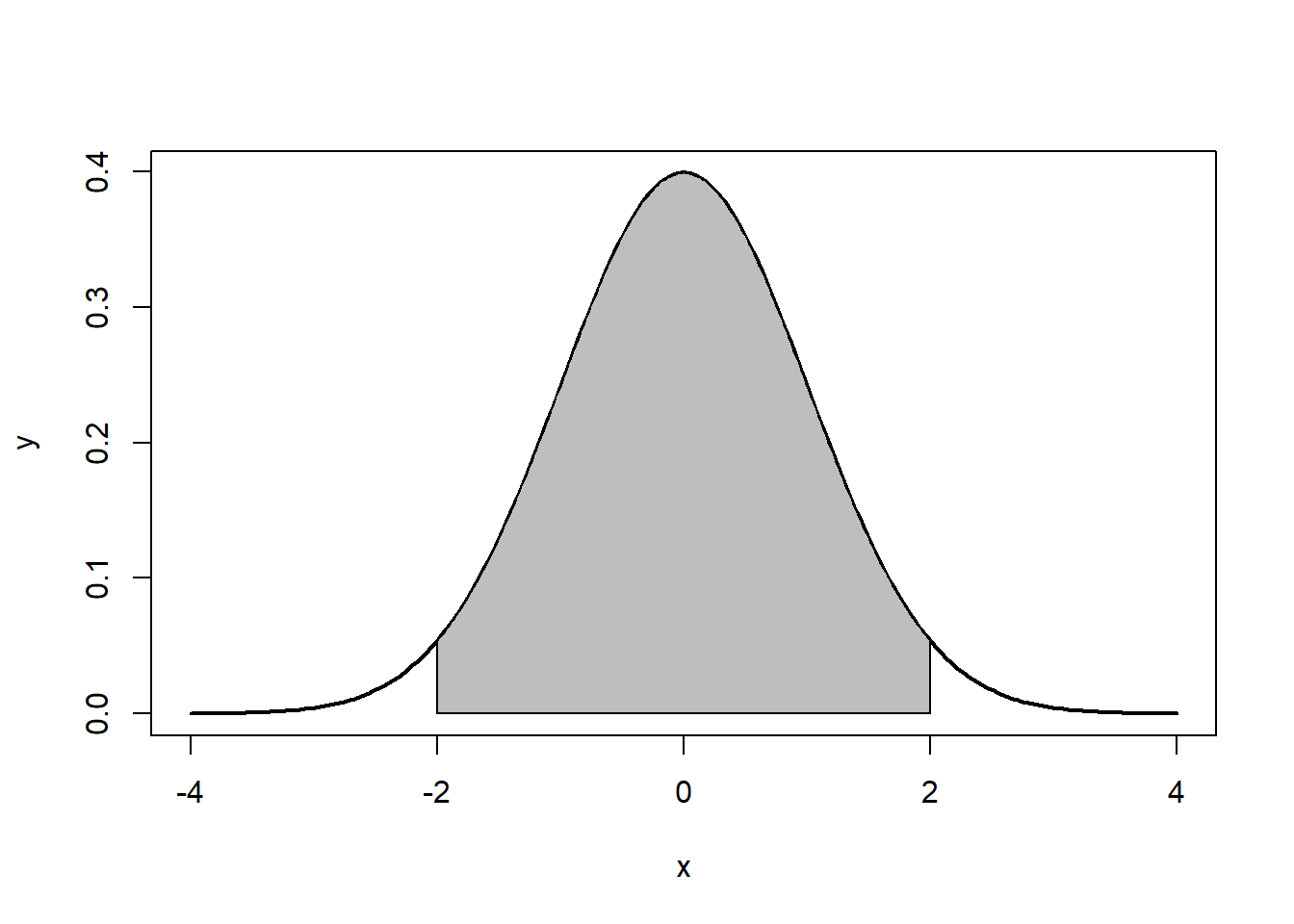
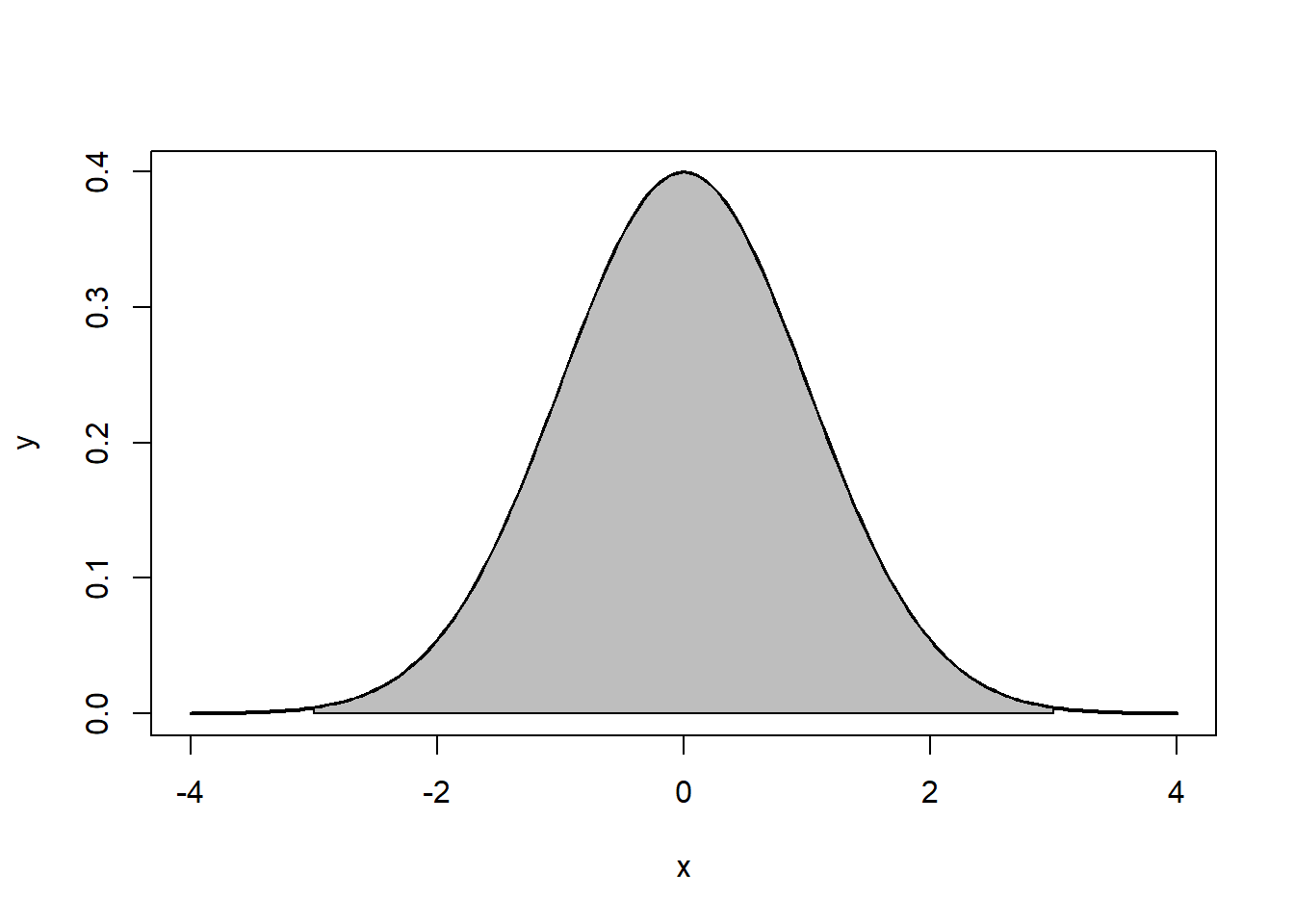
La distribución normal se caracteriza por varias propiedades importantes. La distribución de observaciones es simétrica alrededor de la media μμ; la frecuencia de observaciones es más alta (el modo) a μμ, con valores más extremos ocurriendo con menor frecuencia (esto se puede ver en la Figura?? ); y solo se necesita la media y varianza para caracterizar los datos y probar hipótesis simples.
Las propiedades de la distribución normal
- Es simétrico alrededor de su media y mediana, μμ
- La probabilidad más alta (también conocida como “el modo”) ocurre en su valor medio
- Los valores extremos ocurren en las colas
- Se describe completamente por sus dos parámetros, μμ y σ2σ2
Si se conocen los valores para μμ y σ2σ2, lo que podría ser el caso de una población, entonces podemos calcular una puntuación ZZ para comparar diferencias en μμ y σ2σ2 entre dos distribuciones normales u obtener la probabilidad para un valor dado dado μμ y σ2σ2. Se calcula la puntuación ZZ:
Z=Y−μYσ (5.2) (5.2) Z=Y−μYσ
Por lo tanto, si tenemos una distribución normal con un μμ de 70 y un σ2σ2 de 9, podemos calcular una probabilidad para i=75i=75. Primero calculamos el puntaje ZZ, luego determinamos la probabilidad de ese puntaje con base en la distribución normal.
z <- (75-70)/3
z## [1] 1.666667p <- pnorm(1.67)
p## [1] 0.9525403p <- 1-p
p## [1] 0.04745968Como se muestra, una puntuación de 7575 cae justo fuera de dos desviaciones estándar (>0.95>0.95), y la probabilidad de obtener esa puntuación cuando μ=70μ=70 y σ2=9σ2=9 es poco menos del 5%.
5.2.1 Estandarización de una distribución normal y puntuaciones Z
Una distribución se puede trazar usando las puntuaciones sin procesar que se encuentran en los datos originales. Esa gráfica tendrá una media y una desviación estándar calculadas a partir de los datos originales. Para utilizar la curva normal para determinar funciones de probabilidad y para estadísticas inferenciales vamos a querer convertir esos datos para que estén estandarizados. Estandarizamos para que la distribución sea consistente en todas las distribuciones. Esa estandarización produce un conjunto de puntuaciones que tienen una media de cero y una desviación estándar de uno. Una puntuación estandarizada o Z de 1.5 significa, por lo tanto, que la puntuación es una desviación estándar y media sobre la media. Una puntuación Z de -2.0 significa que la puntuación es de dos desviaciones estándar por debajo de la media.
Como se indica en la fórmula (4.4), la estandarización es un proceso sencillo. Para mover la media de su valor original a una media de cero, todo lo que tienes que hacer es restar la media de cada puntaje. Para estandarizar la desviación estándar a uno todo lo que es necesario es dividir cada puntaje la desviación estándar.
5.2.2 El Teorema del Límite Central
Una propiedad importante de las muestras se asocia con el Teorema del Límite Central (CLT). Imagina por un momento que tenemos una población muy grande (o incluso infinita), de la que podemos sacar tantas muestras como queramos. Según el CLT, a medida que aumenta el tamaño n (número de observaciones) dentro de una muestra extraída de esa población, más se asemejará la distribución de las medias tomadas de muestras de ese tamaño a una distribución normal. Esto se ilustra en la Figura\(\PageIndex{5}\). También tenga en cuenta que la población no necesita tener una distribución normal para que el CLT aplique. Finalmente, una distribución de medias de una población normal será aproximadamente normal en cualquier tamaño de muestra.


