5.3: Inferencias a la Población a partir de la Muestra

Otra implicación clave del Teorema del Límite Central que se ilustra en la Figura\(\PageIndex{5}\) es que la media de las medias de la muestra repetida es la misma, independientemente del tamaño de la muestra, y que la media de las medias de la muestra es la media poblacional (suponiendo un número suficientemente grande de muestras). Esas conclusiones llevan al punto importante de que la media muestral es la mejor estimación de la media poblacional, es decir, la media muestral es una estimación imparcial de la media poblacional. La figura\(\PageIndex{5}\) también ilustra a medida que aumenta el tamaño de la muestra, aumenta la eficiencia de la estimación. A medida que aumenta el tamaño de la muestra, es más probable que la media de cualquier muestra en particular se aproxime a la media poblacional.

Cuando iniciemos nuestra investigación debemos tener en mente alguna población, el conjunto de ítems sobre los que queremos sacar conclusiones. Es posible que queramos saber sobre todos los estadounidenses adultos o sobre los seres humanos (pasado, presente y futuro) o sobre una condición meteorológica específica. Sólo hay una manera de conocer con certeza sobre esa población y es examinar todos los casos que se ajusten a la definición de nuestra población. La mayoría de las veces, sin embargo, no podemos hacer eso —en el caso de los estadounidenses adultos sería muy lento, costoso y logísticamente bastante desafiante, y en los otros dos casos simplemente sería imposible. Nuestra investigación, entonces, a menudo nos obliga a confiar en muestras.

Debido a que confiamos en muestras, las estadísticas inferenciales se basan en la probabilidad. Como\(\PageIndex{5}\) ilustra la Figura, nuestra muestra podría reflejar perfectamente nuestra población; podría ser (y es probable que sea) al menos una aproximación razonable de la población, o la muestra podría desviarse sustancialmente de la población. Aquí se están haciendo dos puntos críticos: las mejores estimaciones que tenemos de nuestros parámetros poblacionales son nuestras estadísticas de muestra, y nunca sabemos con certeza qué tan buena es esa estimación. Tomamos decisiones (estadísticas y del mundo real) basadas en probabilidades.

5.3.1 Intervalos de confianza

Debido a que estamos lidiando con probabilidades, si estamos estimando un parámetro de población utilizando un estadístico de muestra, vamos a querer saber cuánta confianza colocar en esa estimación. Si queremos conocer una media poblacional, pero solo tener una muestra, la mejor estimación de esa media poblacional es la media muestral. Para saber cuánta confianza tener en una muestra media, le ponemos un intervalo de confianza”. Un intervalo de confianza reportará tanto un rango para la estimación como la probabilidad de que el valor de la población caiga en ese rango. Decimos, por ejemplo, que estamos 95% seguros de que el verdadero valor está entre A y B.

Para encontrar ese intervalo de confianza, nos basamos en el error estándar de la estimación. La figura\(\PageIndex{5}\) representa la distribución de los estadísticos muestrales extraídos de muestras repetidas. A medida que aumenta el tamaño de la muestra, las estimaciones se agrupan más cerca del valor real de la población, es decir, la desviación estándar es menor. Podríamos usar la desviación estándar de muestras repetidas para determinar la confianza que podemos tener en cualquier muestra en particular, pero en realidad, no tenemos más probabilidades de extraer muestras repetidas que para estudiar a toda la población. El error estándar, sin embargo, proporciona una estimación de la desviación estándar que tendríamos si sacáramos varias muestras. El error estándar se basa en el tamaño de la muestra y la distribución de observaciones en nuestros datos:

\[SE=s√n(5.3)(5.3)SE=sn\]

donde ss es la desviación estándar de la muestra, y nn es el tamaño (número de observaciones) de la muestra.

El error estándar se puede interpretar como una desviación estándar. Si tenemos una muestra grande, podemos decir que el 68.26% de todas nuestras muestras (suponiendo que dibujamos muestras repetidas) caerían dentro de un error estándar de nuestro estadístico de muestra o que 95.44% caería dentro de dos errores estándar.

Si nuestro tamaño de muestra no es grande, en lugar de usar puntuaciones z para estimar intervalos de confianza, usamos puntajes t para estimar el intervalo. Las puntuaciones T se calculan igual que la puntuación z, pero nuestra interpretación de ellas es ligeramente diferente. La fórmula del intervalo de confianza es:

\[¯x+/−SEx∗t(5.4)(5.4)x¯+/−SEx∗t\]

Para encontrar el valor apropiado para t, necesitamos decidir qué nivel de confianza queremos (generalmente 95%) y nuestros grados de libertad (df), que es n−1n−1. Podemos encontrar un intervalo de confianza con R usando la función t.test. Por defecto, t.test probará la hipótesis de que la media de nuestra variable de interés (glbcc_risk) es igual a cero. También encontrará la puntuación media y un intervalo de confianza para la variable glbcc_risk:

t.test(ds$glbcc_risk)

## 
##  One Sample t-test
## 
## data:  ds$glbcc_risk
## t = 97.495, df = 2535, p-value < 0.00000000000000022
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
##  5.826388 6.065568
## sample estimates:
## mean of x 
##  5.945978

Pasando de abajo hacia arriba en la salida vemos que nuestra puntuación media es de 5.95. A continuación, vemos que el intervalo de confianza del 95% está entre 5.83 y 6.07. Estamos, por lo tanto, 95% seguros de que la media poblacional está en algún lugar entre esos dos puntajes. La primera parte de la salida prueba la hipótesis nula de que el valor medio es igual a cero —un tema que cubriremos en la siguiente sección.

5.3.2 La lógica de las pruebas de hipótesis

Podemos usar el mismo conjunto de herramientas para probar hipótesis. En esta sección, se introduce la lógica de las pruebas de hipótesis. En el siguiente capítulo, lo abordamos con más detalle. Recuerda que una hipótesis es una afirmación sobre la forma en que es el mundo y que puede ser verdadero o falso. Las hipótesis generalmente se deducen de nuestra teoría y si se confirman nuestras expectativas, ganamos confianza en nuestra teoría. La prueba de hipótesis es donde nuestras ideas se encuentran con el mundo real.

Debido a la naturaleza de las estadísticas inferenciales, no podemos probar directamente hipótesis, sino que podemos probar una hipótesis nula. Si bien una hipótesis es una declaración de una relación esperada entre dos variables, la hipótesis nula es una afirmación que dice que no hay relación entre las dos variables. Una hipótesis nula podría decir: A medida que XX aumenta, YY no cambia. (Discutiremos más este tema en el siguiente capítulo, pero queremos entender la lógica del proceso aquí.)

Supongamos que un director quiere reducir el ausentismo en su escuela y ofrece un programa de incentivos para una asistencia perfecta. Antes del programa, supongamos que la tasa de asistencia era de 85%. Después de tener el nuevo programa implementado por un tiempo, quiere saber cuál es la tasa actual por lo que toma una muestra de días y estima que la tasa de asistencia actual es de 88%. Su hipótesis de investigación es: la tasa de asistencia ha aumentado desde el anuncio del nuevo programa (es decir, la asistencia es superior al 85%). Su hipótesis nula es que la tasa de asistencia no ha subido desde el anuncio del nuevo programa (es decir, la asistencia es menor o igual al 85%). Al principio, parece que su hipótesis nula es errónea (88% > 85%) (88% > 85%), pero como estamos usando una muestra, es posible que el verdadero valor poblacional sea menor al 85%. A partir de su muestra, ¿qué tan probable es que el verdadero valor poblacional sea inferior al 85%? Si la probabilidad es pequeña (y recuerda que siempre habrá alguna posibilidad), entonces decimos que nuestra hipótesis nula es incorrecta, es decir, rechazamos nuestra hipótesis nula, pero si la probabilidad es razonable aceptamos nuestra hipótesis nula. El estándar que normalmente usamos para hacer esa determinación es .05 — queremos menos de una probabilidad de .05 de que podríamos haber encontrado nuestro valor de muestra (aquí 88%) si nuestro valor hipotético nulo (85%) es cierto para la población. Utilizamos el estadístico t para encontrar esa probabilidad. La fórmula es:

\[t=x−μse(5.5)(5.5)t=x−μse\]

Si volvemos a la salida presentada anteriormente sobre glbcc_risk, podemos ver que R probó la hipótesis nula de que el valor verdadero de la población glbcc_risk es igual a cero. Reporta t = 97.495 y un valor p de 2.2e-16. Este valor p es menor que .05, por lo que podemos rechazar nuestra hipótesis nula y estar muy seguros de que el valor verdadero de la población es mayor que cero.% de los ítems anteriores se puede hacer dinámico.

5.3.3 Algunas notas misceláneas sobre las pruebas de hipótesis

Antes de suspender nuestra discusión sobre las pruebas de hipótesis, hay algunos cabos sueltos que amarrar. Primero, podrías estar preguntándote de dónde viene el estándar .05 de las pruebas de hipótesis. ¿Hay algo de magia en ese número? La respuesta es no “; .05 es simplemente el estándar, pero algunos investigadores reportan .10 ó .01. Sin embargo, generalmente se considera que el valor p de .05 proporciona un equilibrio razonable entre hacer casi imposible rechazar una hipótesis nula y abarrotar con demasiada facilidad nuestra caja de conocimiento con cosas que creemos que están relacionadas pero que en realidad no lo están. Incluso usando el estándar .05 significa que el 5% de las veces cuando rechazamos la hipótesis nula, estamos equivocados, no hay relación. (Además de darte una pausa preguntándote en qué nos equivocamos, también debería ayudarte a ver por qué la ciencia considera que la replicación es tan importante).

Segundo, como acabamos de dar a entender, cada vez que tomemos la decisión de aceptar o rechazar nuestra hipótesis nula, podríamos estar equivocados. Las probabilidades nos dicen que si p=0.05p=0.05, 5% de las veces cuando rechazamos la hipótesis nula, estamos equivocados porque en realidad es verdad. Llamamos a ese tipo de error un Error de Tipo I. No obstante, cuando aceptamos la hipótesis nula, también podríamos estar equivocados —puede haber una relación dentro de la población. A eso lo llamamos Error Tipo II. Como debe ser evidente, existe un compromiso entre ambos. Si decidimos usar un valor p de .01 en lugar de .05, cometemos menos errores de Tipo I, solo uno de cada 100, en lugar de 5 sobre 100. Sin embargo, eso también significa que aumentamos en .04 la probabilidad de que estemos aceptando una hipótesis nula que es falsa, un Error Tipo II. Para reformular el párrafo anterior: .05 normalmente se considera un equilibrio razonable entre la probabilidad de cometer Errores de Tipo I en contraposición a Errores de Tipo II. Por supuesto, si la consecuencia de un tipo de error u otro es mayor, entonces se puede ajustar el valor p.

Tercero, al probar hipótesis, podemos usar ya sea una prueba de una cola o una prueba de dos colas. La pregunta es si todo el .05 va en un sastre se divide uniformemente entre las dos colas (haciendo, efectivamente, el valor p igual a .025). En términos generales, si tenemos una hipótesis direccional (por ejemplo, a medida que X aumenta también lo hace Y), usaremos una prueba de una cola. Si estamos esperando una relación positiva, pero encontramos una relación negativa fuerte, generalmente concluimos que tenemos una peculiaridad muestral y que la relación es nula, más que lo contrario de lo que esperábamos. Si, por alguna razón, tienes una hipótesis que no especifica la dirección, te interesarían los valores en cualquiera de las colas y utilizarías una prueba de dos colas.

5.4 Diferencias entre grupos

Además de la covarianza y correlación (discutida en el siguiente capítulo), también podemos examinar las diferencias en algunas variables de interés entre dos o más grupos. Por ejemplo, es posible que queramos comparar la media de la variable de riesgo de cambio climático percibida para hombres y mujeres. En primer lugar, podemos examinar estas variables visualmente.

Según lo codificado en nuestro conjunto de datos, el género (género) es una variable numérica con un 1 para los hombres y 0 para las mujeres. Sin embargo, podemos querer convertir género en una variable categórica con etiquetas para Female y Male, a diferencia de una variable numérica codificada como 0's y 1's Para ello hacemos una nueva variable y usamos el comando factor, que le dirá a R que la nueva variable es una variable categórica. Entonces le diremos a R que esta nueva variable tiene dos niveles o factores, Masculino y Femenino. Finalmente, etiquetaremos los factores de nuestra nueva variable y la nombraremos f.gend.

ds$f.gend <- factor(ds$gender, levels = c(0, 1), labels = c("Female","Male"))

Luego podemos observar diferencias en las distribuciones de riesgo percibido para hombres y mujeres mediante la creación de curvas de densidad:

library(tidyverse)
ds %>%
  drop_na(f.gend) %>%
  ggplot(aes(glbcc_risk)) +
  geom_density() +
  facet_wrap(~ f.gend, scales = "fixed")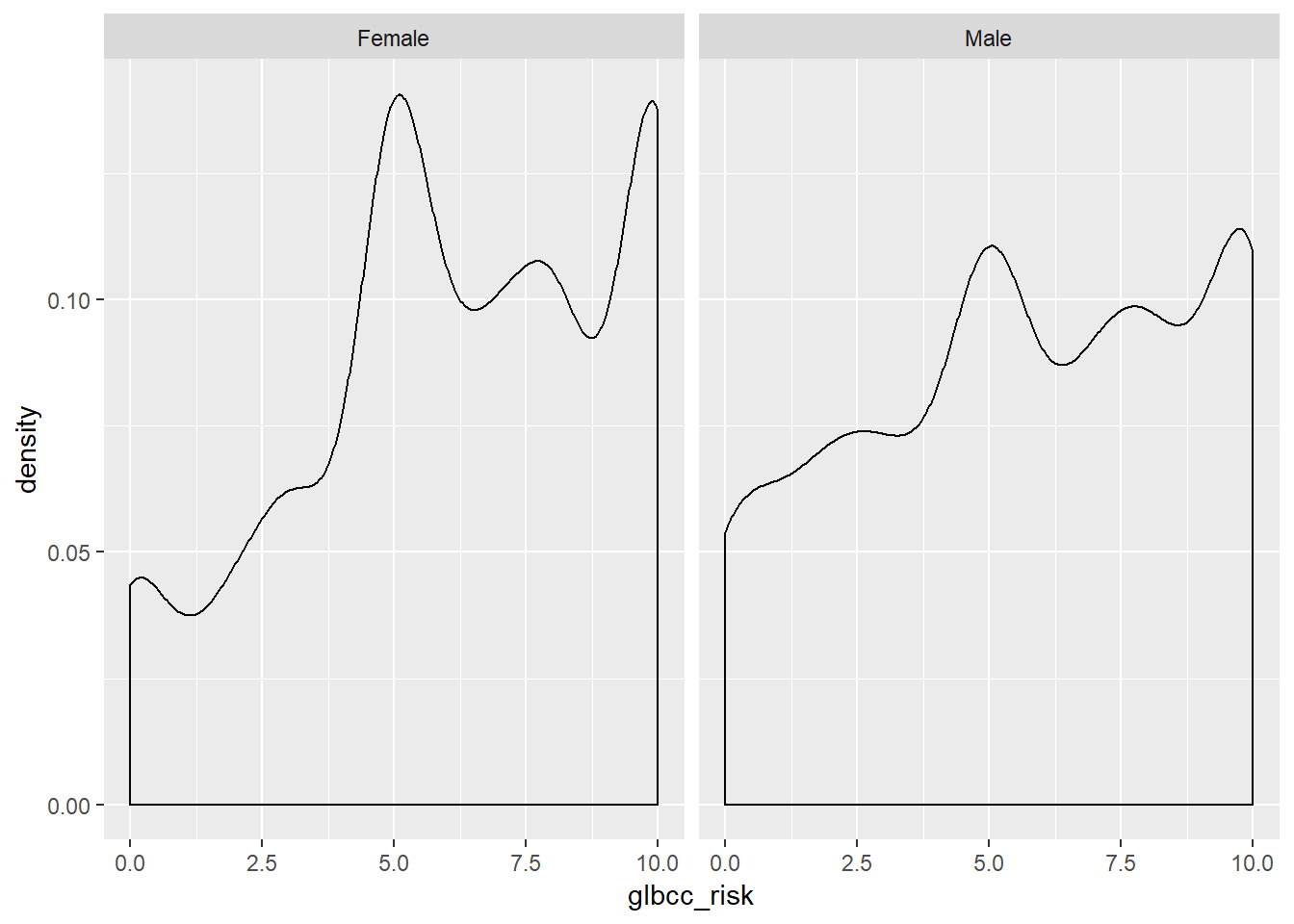

Figura\(\PageIndex{7}\): Gráfica de Densidad del Riesgo de Cambio Climático por Género

Con base en las parcelas de densidad, parece que existen algunas diferencias entre hombres y mujeres con respecto al riesgo percibido de cambio climático. También podemos usar el comando by para ver la media de riesgo de cambio climático para hombres y mujeres.

by(ds$glbcc_risk, ds$f.gend, mean, na.rm=TRUE)

## ds$f.gend: Female
## [1] 6.134259
## -------------------------------------------------------- 
## ds$f.gend: Male
## [1] 5.670577

Nuevamente parece haber una diferencia, ya que las hembras perciben mayor riesgo en promedio (6.13) que los machos (5.67). Sin embargo, queremos saber si estas diferencias son estadísticamente significativas. Para probar la significancia estadística de la diferencia entre grupos, se utiliza una prueba t.

5.4.1 pruebas t

La prueba t se basa en la distribución tt. La distribución tt, también conocida como distribución tt de Student, es la distribución de probabilidad para estimaciones muestrales. Tiene propiedades similares y se relaciona con, la distribución normal. La distribución normal se basa en una población donde se conocen μμ y σ2σ2; sin embargo, la distribución tt se basa en una muestra donde se estiman μμ y σ2σ2, como la media ¯XX¯ y varianza s2xsx2. La media de la distribución tt, al igual que la distribución normal, es 00, pero la varianza, s2xsx2, está condicionada por n−1n−1 grados de libertad (df). Grados de libertad son los valores utilizados para calcular estadísticas que son “libres” para variar. La distribución de ¹¹ A tt se acerca a la distribución normal estándar a medida que aumenta el número de grados de libertad.

En resumen, queremos conocer la diferencia de medias entre machos y hembras, d=¯xM−¯xFD=x¯m−x¯f, y si esa diferencia es estadísticamente significativa. Esto equivale a una prueba de hipótesis donde nuestra hipótesis de trabajo, H1H1, es que los hombres son menos propensos que las mujeres a ver el cambio climático como riesgoso. La hipótesis nula, JAHA, es que no hay diferencia entre hombres y mujeres en cuanto a los riesgos asociados al cambio climático. Para probar H1H1 utilizamos la prueba t, que se calcula:

t=¯xM−¯xFSED (5.6) (5.6) T=x¯m−x¯FSED

Donde seDSED es la de las diferencias estimadas entre los dos grupos. Para estimar SEDSed, necesitamos el SE de la media estimada para cada grupo. El SE se calcula:

se=s√n (5.7) (5.7) se=SN

donde ss es el s.d. de la variable. H1H1 afirma que existe una diferencia entre machos y hembras, por lo que bajo H1H1 se espera que t>0t>0 ya que cero es la media de la distribución tt. Sin embargo, bajo JAHA se espera que t=0t=0.

Podemos calcular esto en R. Primero, calculamos el tamaño nn para machos y hembras. Después calculamos el SE para machos y hembras.

n.total <- length(ds$gender)
nM <- sum(ds$gender, na.rm=TRUE)
nF <- n.total-nM
by(ds$glbcc_risk, ds$f.gend, sd, na.rm=TRUE)

## ds$f.gend: Female
## [1] 2.981938
## -------------------------------------------------------- 
## ds$f.gend: Male
## [1] 3.180171

sdM <- 2.82
seM <- 2.82/(sqrt(nM))
seM

## [1] 0.08803907

sdF <- 2.35
seF <- 2.35/(sqrt(nF))
seF

## [1] 0.06025641

A continuación, necesitamos calcular el sedado:sed=√SE2M+SE2F (5.8) (5.8) sed=SEM2+SEF2

seD <- sqrt(seM^2+seF^2)
seD

## [1] 0.1066851

Finalmente, podemos calcular nuestro puntaje tt, y usar la función t.test para verificar.

by(ds$glbcc_risk, ds$f.gend, mean, na.rm=TRUE)

## ds$f.gend: Female
## [1] 6.134259
## -------------------------------------------------------- 
## ds$f.gend: Male
## [1] 5.670577

meanF <- 6.96 
meanM <- 6.42
t <- (meanF-meanM)/seD
t

## [1] 5.061625

t.test(ds$glbcc_risk~ds$gender)

## 
##  Welch Two Sample t-test
## 
## data:  ds$glbcc_risk by ds$gender
## t = 3.6927, df = 2097.5, p-value = 0.0002275
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  0.2174340 0.7099311
## sample estimates:
## mean in group 0 mean in group 1 
##        6.134259        5.670577

Para la diferencia en el riesgo percibido entre mujeres y hombres, tenemos un valor tt de 4.6. Este resultado es mayor a cero, como se esperaba por H1H1. Además, como se muestra en la salida de t.test el valor pp —la probabilidad de obtener nuestro resultado si la diferencia poblacional fue 00—es extremadamente bajo en .0002275 (es decir, lo mismo que 2.275e-04). Por lo tanto, rechazamos la hipótesis nula y concluimos que existen diferencias (en promedio) en las formas en que hombres y mujeres perciben el riesgo del cambio climático.

5.5 Resumen

En este capítulo obtuvimos una comprensión de las estadísticas inferenciales, cómo utilizarlas para colocar intervalos de confianza alrededor de una estimación y una visión general de cómo utilizarlas para probar hipótesis. En el siguiente capítulo, pasamos, de manera más formal, a probar hipótesis utilizando tabulaciones cruzadas y comparando medios de diferentes grupos. Luego continuamos explorando las pruebas de hipótesis y la construcción de modelos mediante análisis de regresión.

---

8. Es importante tener en cuenta que, para fines de construcción teórica, la población de interés puede no ser finita. Por ejemplo, si teorizas sobre las propiedades generales del comportamiento humano, muchos de los miembros de la población humana aún no están (o ya no están) vivos. De ahí que no sea posible incluir a toda la población de interés en su investigación. Por lo tanto, confiamos en muestras. ↩
9. Por supuesto, también necesitamos estimar los cambios —tanto graduales como abruptos— en la forma en que las personas se comportan a lo largo del tiempo, que es la provincia del análisis de series temporales. ↩
10. Wei Wang, David Rothschild, Sharad Goel y Andrew Gelman (2014)” Pronosticando elecciones con encuestas no representativas”, preimpresión enviada al International Journal of Forecasting 31 de marzo de 2014. ↩
11. En una prueba de diferencia de medias en dos grupos, “usamos” una observación cuando separamos las observaciones en dos grupos. De ahí que el denominador refleje la pérdida de esa observación gastada: n-1. ↩