Saltar al contenido principal
LibreTexts Español

6.1: Tabulación cruzada

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    150290

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    6.1 Tabulación cruzada

    Para determinar si existe una asociación entre dos variables medidas a nivel nominal u ordinal, utilizamos tabulación cruzada y un conjunto de estadísticas de apoyo. Una tabulación cruzada (o solo tabulación cruzada) es una tabla que analiza la distribución de dos variables simultáneamente. El Cuadro 6.1 proporciona un diseño de muestra de una tabla de 2 X 2.

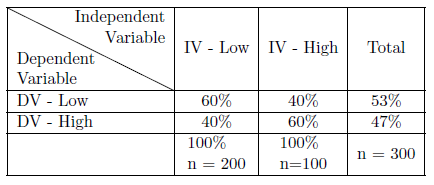
    iv-dv.png
    Figura\(\PageIndex{1}\): Disposición de la tabla de muestra

    Como ilustra la Tabla 6.1, se configura una tabulación cruzada para que la variable independiente esté en la parte superior, formando columnas, y la variable dependiente esté en el lado, formando filas. Hacia la esquina superior izquierda de la tabla se encuentran las categorías variables bajas o negativas. Generalmente, una tabla se mostrará en un formato de porcentaje. Los marginales para una tabla son los totales de columna y los totales de fila y son los mismos que una distribución de frecuencia sería para esa variable. Cada clasificación cruzada informa cuántas observaciones tienen esa característica compartida. Los grupos de clasificación cruzada se denominan celdas, por lo que la Tabla 6.1 es una tabla de cuatro celdas.

    Una tabla como la Tabla 6.1 proporciona una base para comenzar a responder a la pregunta de si nuestras variables independientes y dependientes están relacionadas. Recuerda que nuestra hipótesis nula dice que no hay relación entre nuestro IV y nuestro DV. Mirando el Cuadro 6.1, podemos decir de aquellos bajos en el IV, 60% de ellos también estarán por debajo en el DV; y que los altos en el IV serán bajos en el DV 40% de las veces. Nuestra hipótesis nula dice que no debería haber diferencia, pero en este caso, hay una diferencia del 20% por lo que parece que nuestra hipótesis nula es incorrecta. Sin embargo, lo que aprendimos en nuestro capítulo de estadísticas inferenciales nos dice que todavía es posible que la hipótesis nula sea cierta. La pregunta es ¿qué tan probable es que podamos tener una diferencia del 20% en nuestra muestra aunque la hipótesis nula sea cierta? 12

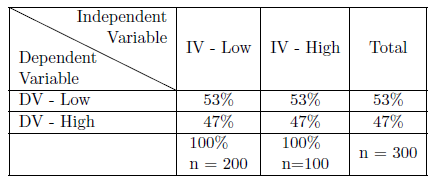
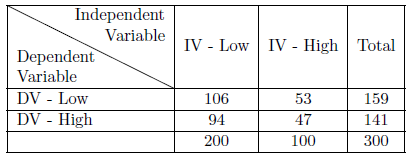
    Utilizamos el estadístico chi-cuadrado para probar nuestra hipótesis nula al usar tabulaciones cruzadas. Para encontrar chi-cuadrado (χ2χ2), comenzamos asumiendo que la hipótesis nula es verdadera y encontramos las frecuencias esperadas para cada celda en nuestra tabla. Lo hacemos utilizando una metodología posterior basada en los marginales de nuestra variable dependiente. Vemos que 53% de nuestra muestra total es baja en la variable dependiente. Si nuestra hipótesis nula es correcta, entonces donde se ubica uno en la variable independiente no debería importar: 53% de los que son bajos en el IV deben ser bajos en el DV y 53% de los que son altos en el IV deben ser bajos en el DV. Los cuadros 6.2 y 6.3 ilustran este patrón. Para encontrar la frecuencia esperada para cada celda, simplemente multiplicamos el porcentaje de celdas esperado por el número de personas en cada categoría de la IV: la frecuencia esperada para la celda baja-baja es .53*200=106.53*200=106; para la celda baja-alta, es .47*200=94.47*200=94; para la celda baja-alta es .53*100=53.53∗ 100=53; y para la celda alto-alta, la frecuencia esperada es .47*100=47.47*100=47. (Ver Tabla 6.2 y 6.3).

    La fórmula para el chi-cuadrado toma la frecuencia esperada para cada una de las celdas y le resta la frecuencia observada, cuadra esas diferencias, divide por la frecuencia esperada y suma esos valores:

    χ2=( O−E) 2E (6.1) (6.1) χ2=( O−E) 2E

    donde:

    χ2χ2 = El estadístico de prueba

    = El Operador de Suma

    OO = Frecuencias observadas

    EE = Frecuencias esperadas

    iv-dv2.png
    Figura\(\PageIndex{2}\): Ejemplo de Diseño de Tabla Hipotetizada Nulo como Porcentajes
    iv-dv3.png
    Figura\(\PageIndex{3}\): Disposición de tabla hipotética nula de muestra como recuentos

    En el cuadro 6.4 se proporcionan esos cálculos. Muestra un chi-cuadrado final de 10.73. Con ese chi-cuadrado, podemos ir a una tabla chi-cuadrada para determinar si aceptar o rechazar la hipótesis nula. Antes de ir a esa mesa chi-cuadrada, tenemos que averiguar dos cosas. Primero, necesitamos determinar el nivel de significancia que queremos, presumiblemente .05. Segundo, necesitamos determinar nuestros grados de libertad. Proporcionaremos más sobre ese concepto a medida que avancemos, pero por ahora, sepa que es el número de filas menos una veces el número de columnas menos una. En este caso, tenemos (2−1) (2−1) =1 (2−1) (2−1) =1 grado de libertad.

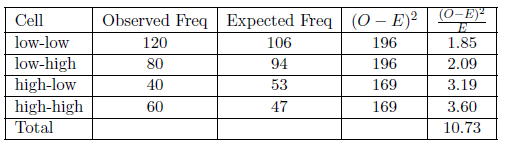
    iv-dv4.png
    Figura\(\PageIndex{4}\): Cálculo de Chi-cuadrado

    El Cuadro 6.9 (al final de este capítulo) es una tabla chi-cuadrada que muestra los valores críticos para diversos niveles de significancia y grados de libertad. El valor crítico para un grado de libertad con un nivel de significancia .05 es 3.84. Dado que nuestro chi-cuadrado es mayor que eso podemos rechazar nuestra hipótesis nula - hay menos de una probabilidad .05 de que podríamos haber encontrado los resultados en nuestra muestra si no hay relación en la población. De hecho, si seguimos la fila por un grado de libertad transversal, vemos que podemos rechazar nuestra hipótesis nula incluso en el nivel de significación .005 y, casi pero no del todo, en el nivel de significancia .001.

    Habiendo rechazado la hipótesis nula, creemos que existe una relación entre las dos variables, pero aún queremos saber qué tan fuerte es esa relación. Se utilizan medidas de asociación para determinar la fuerza de una relación. Un tipo de medida de asociación se basa en un modelo de covariación tal como se detalla en las Secciones 6.2 y 6.3. Los modelos de covariación son modelos direccionales y requieren medidas de nivel ordinales o de intervalo; de lo contrario, las variables no tienen dirección. Aquí consideramos modelos alternativos.

    Si una o ambas de nuestras variables son nominales, no podemos especificar el cambio direccional. Aún así, podríamos ver un patrón de cambio reconocible en una variable a medida que la otra variable varía. Las mujeres podrían estar más preocupadas por el cambio climático que los hombres, por ejemplo. Para ese tipo de casos, podemos usar un modelo de reducción en el error o una reducción proporcional en el error (PRE). Consideramos qué tan bien predecimos usando un modelo ingenuo (asumiendo que no hay relación) y lo comparamos con cuánto mejor predecimos cuando usamos nuestra variable independiente para hacer esa predicción. Estas medidas de asociación solo oscilan entre 0−1.00−1.0, ya que el signo indica de otro modo la dirección. Generalmente, utilizamos este tipo de medida cuando al menos una de nuestras variables es nominal, pero también usaremos una medida modelo PRE, r2r2, en el análisis de regresión. Lambda es una medida de asociación prebasada de uso común para datos de nivel nominal, pero puede subestimar la relación en algunas circunstancias.

    Otro conjunto de medidas de asociación adecuadas para datos de nivel nominal se basa en chi-cuadrado. La V de Cramer es un indicador simple basado en chi cuadrado, pero al igual que el propio chi-cuadrado, su valor se ve afectado por el tamaño de la muestra y las dimensiones de la tabla. Phi corrige el tamaño de la muestra pero es apropiado solo para una tabla de 2 X 2. El coeficiente de contingencia, C, también corrige el tamaño de la muestra y se puede aplicar a tablas más grandes, pero requiere una tabla cuadrada, es decir, el mismo número de filas y columnas.

    Si tenemos datos de nivel ordinal, podemos usar un modelo de covariación, pero el modelo específico desarrollado a continuación en la Sección 6.3 analiza cómo se distribuyen las observaciones alrededor de sus medias. Como no podemos encontrar una media para los datos de nivel ordinal, necesitamos una alternativa. Gamma se usa comúnmente con datos de nivel ordinal y proporciona un resumen que compara cuántas observaciones caen alrededor de la diagonal en la tabla que admite una relación positiva (por ejemplo, observaciones en la celda baja-baja y las celdas alta-alta) en oposición a las observaciones que siguen a la diagonal negativa (por ejemplo, la célula bajo-alta y las células alto-bajas). Gamma varía de −1.0−1.0 a +1.0+1.0. \

    Las tabulaciones cruzadas y sus estadísticas asociadas se pueden calcular usando R. En este ejemplo continuamos usando el conjunto de datos de Cambio Climático Global (ds). El conjunto de datos incluye medidas de los encuestados: género (femenino = 0, masculino = 1); riesgo percibido que representa el cambio climático, o glbcc_risk (0 = No riesgo; 10 = riesgo extremo) e ideología política (1 = fuerte liberal, 7 = fuerte conservador). Aquí analizamos si existe una relación entre género y la variable glbcc_risk. La variable glbcc_risk tiene once categorías; para que la tabla sea más manejable, la recodificamos en cinco categorías.

    #  Factor the gender variable
ds$f.gend <- factor(ds$gender, levels=c(0,1), labels = c("Women", "Men"))

#  recode glbcc_risk to five categories
library(car)
ds$r.glbcc_risk <- car::recode(ds$glbcc_risk, "0:1=1; 2:3=2; 4:6=3; 7:8:=4;
                          9:10=5; NA=NA")

    Usando la función table, producimos una tabla de frecuencias que refleja la relación entre género y la variable glbccrisk recodificada.

    #  create the table
table(ds$r.glbcc_risk, ds$f.gend)
    ##    
##     Women Men
##   1   134 134
##   2   175 155
##   3   480 281
##   4   330 208
##   5   393 245
    #  create the table as an R Object
glbcc.table <- table(ds$r.glbcc_risk, ds$f.gend)

    Esta tabla es difícil de interpretar debido a que el número de hombres y mujeres son diferentes. Para que la tabla sea más fácil de interpretar, la convertimos a porcentajes utilizando la función prop.table. Al mirar la nueva tabla, podemos ver que hay más hombres en el extremo inferior de la escala de riesgo percibido y más mujeres en el extremo superior.

    #  Multiply by 100
prop.table(glbcc.table, 2) * 100
    ##    
##         Women       Men
##   1  8.862434 13.098729
##   2 11.574074 15.151515
##   3 31.746032 27.468231
##   4 21.825397 20.332356
##   5 25.992063 23.949169

    La tabla porcentual sugiere que existe una relación entre las dos variables, pero también ilustra el desafío de depender de las diferencias porcentuales para determinar la significancia de esa relación. Entonces, para probar nuestra hipótesis nula, calculamos nuestro chi cuadrado usando la función chisq.test.

    #  Chi Square Test
chisq.test(glbcc.table)
    ## 
##  Pearson's Chi-squared test
## 
## data:  glbcc.table
## X-squared = 21.729, df = 4, p-value = 0.0002269

    R reporta nuestro chiquare para igualar 21.73. También nos dice que tenemos 4 grados de libertad y un valor p de .0002269. Dado que ese valor p es sustancialmente menor que .05, podemos rechazar nuestra hipótesis nula con gran confianza. Existe, evidentemente, una relación entre género y riesgo percibido de cambio climático.

    Por último, queremos saber qué tan fuerte es la relación. Utilizamos la función assocstats para obtener varias medidas de asociación. Dado que la tabla no es una tabla de 2 X 2 ni un cuadrado, ni phi ni el coeficiente de contingencia es apropiado, pero podemos reportar V. La V de Cramer es .093, lo que indica una relación relativamente débil entre género y la variable de riesgo de cambio climático global percibida.

    library(vcd)
assocstats(glbcc.table)
    ##                     X^2 df   P(> X^2)
## Likelihood Ratio 21.494  4 0.00025270
## Pearson          21.729  4 0.00022695
## 
## Phi-Coefficient   : NA 
## Contingency Coeff.: 0.092 
## Cramer's V        : 0.093

    6.1.1 Crosstabulation y Control

    En el Capítulo 2 hablamos de la importancia del control experimental si queremos hacer declaraciones causales. En los diseños experimentales, nos basamos en el control físico y la aleatorización para proporcionar ese control para darnos confianza en la naturaleza causal de cualquier relación que encontremos. Con diseños cuasi-experimentales, sin embargo, no tenemos ese tipo de control y tenemos que preguntarnos si alguna relación que encontremos podría ser espuria. En ese punto, prometimos que la situación no es desesperada con diseños cuasi-experimentales y que existen sustitutos estadísticos para el control que naturalmente se nos brinda en los diseños experimentales. En esta sección, describiremos ese proceso al usar la tabulación cruzada. Primero veremos algunos datos hipotéticos para obtener algunos ejemplos claros de lo que podría suceder cuando controlas una variable explicativa alternativa antes de mirar un ejemplo real usando R.

    El proceso utilizado para controlar una variable explicativa alternativa, comúnmente conocida como tercera variable, es sencillo. Para controlar una tercera variable, primero construimos nuestra tabla original entre nuestras variables independientes y dependientes. Luego clasificamos nuestros datos en subconjuntos basados en las categorías de nuestra tercera variable y reconstruimos nuevas tablas usando nuestro IV y DV para cada subconjunto de nuestros datos.

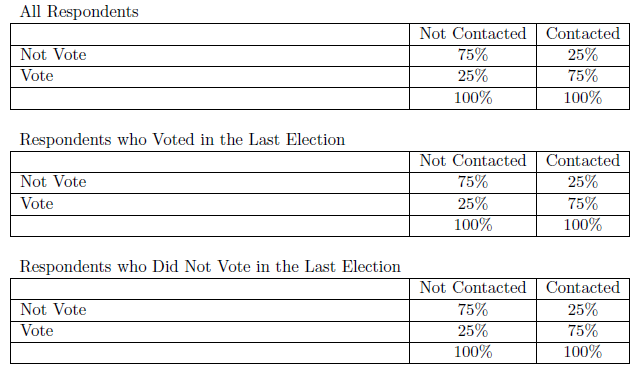
    Supongamos que planteamos la hipótesis de que las personas que son contactadas para votar tienen más probabilidades de votar. El Cuadro 6.5 ilustra lo que podríamos encontrar. (Recuerde que todos estos datos son fabricados para ilustrar nuestros puntos.) Según la primera mesa, las personas que son contactadas tienen 50% más de probabilidades de votar que las que no lo son. Pero, un escéptico podría decir que las campañas apuntan a votantes anteriores para el contacto y que los votantes anteriores tienen más probabilidades de votar en elecciones posteriores. Ese escéptico está argumentando que la relación entre contacto y voto es espuria y que la verdadera causa del voto es el historial de votación. Para probar esa teoría, controlamos el historial de votación clasificando a los encuestados en dos conjuntos: los que votaron en la última elección y los que no. Luego reconstruimos la tabla original para los dos conjuntos de encuestados. Las nuevas mesas indican que los electores anteriores tienen 50% más probabilidades de votar cuando se contactan y que los que no votaron anteriormente tienen 50% más probabilidades de votar cuando se contactan. El escéptico está equivocado; el patrón encontrado en nuestros datos originales persiste incluso después de controlar para la explicación alternativa. Seguimos siendo reacios a usar el lenguaje causal porque otro escéptico podría tener otra explicación alternativa (lo que requeriría que pasemos por el mismo proceso con la nueva tercera variable), pero sí tenemos más confianza en la posible naturaleza causal de la relación entre contacto y voto.

    El siguiente ejemplo pone a prueba la hipótesis de que quienes son optimistas sobre el futuro tienen más probabilidades de votar por el titular que aquellos que son pesimistas. El cuadro 6.6 muestra que las personas optimistas tienen 25% más probabilidades de votar por el titular que las personas pesimistas. Pero nuestro amigo escéptico podría argumentar que los sentimientos sobre el mundo no son tan importantes como las condiciones de la vida real. Las personas con empleo votan por el titular con más frecuencia que las que no tienen trabajo y, por supuesto, las que tienen un empleo tienen más probabilidades de sentirse bien con el mundo. Para probar esa alternativa, controlamos si el encuestado tiene un trabajo y reconstruimos nuevas tablas. Cuando lo hacemos, encontramos que entre los que tienen un empleo, el 70% vota por el titular -independientemente de su nivel de optimismo sobre el mundo-. Y, entre los que no tienen empleo, el 40% vota por el titular, independientemente de su optimismo. Es decir, después de controlar la situación laboral, no existe relación entre el nivel de optimismo y el comportamiento electoral. La relación original fue espuria.

    control1.png
    Figura\(\PageIndex{5}\): Controlar para una tercera variable: nada cambia
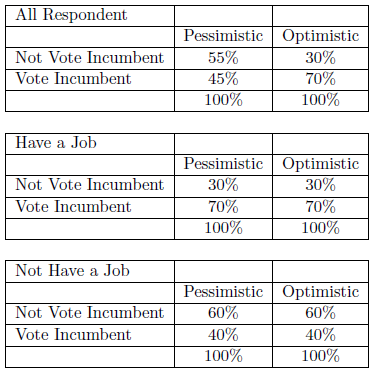
    control2.png
    Figura\(\PageIndex{6}\): Control para una Tercera Variable: Espuria

    Un tercer resultado de controlar para una tercera variable podría ser alguna forma de interacción o efecto de especificación. La tercera variable afecta cómo se relacionan las dos primeras, pero no socavan completamente la relación original. Por ejemplo, podríamos encontrar que la relación original es más fuerte para una categoría de la variable de control que para otra -o incluso estar presente en un caso y no en el otro. El patrón también podría sugerir que ambas variables influyen en la variable dependiente, pareciéndose a alguna forma de causalidad conjunta. De hecho, es posible que tu relación parezca nula en tu tabla original, pero cuando controlas podrías encontrar una relación positiva para una categoría de tu variable de control y negativa para otra.

    Usando un ejemplo de la encuesta Clima y Clima, podríamos plantear la hipótesis de que los liberales tienen más probabilidades de pensar que los gases de efecto invernadero están causando el calentamiento global. Comenzamos recodificando la ideología de 7 niveles a 3, luego construimos una tabla de frecuencias y la convertimos en una tabla de porcentajes de la relación.

    #  recode variables ideology to 3 categories
library(car)
ds$r.ideol<-car::recode(ds$ideol, "1:2=1; 3:5=2; 6:7=3; NA=NA")

#  factor the variables to add labels.
ds$f.ideol<- factor(ds$r.ideol, levels=c(1, 2, 3), labels=c("Liberal", 
                        "Moderate", "Conservative"))
ds$f.glbcc <- factor(ds$glbcc, levels=c(0, 1), 
                          labels = c("GLBCC No", "GLBCC Yes"))

#  3 Two variable table glbcc~ideology
v2.glbcc.table <- table(ds$f.glbcc, ds$f.ideol)
v2.glbcc.table
    ##            
##             Liberal Moderate Conservative
##   GLBCC No       26      322          734
##   GLBCC Yes     375      762          305
    #  Percentages by Column
prop.table(v2.glbcc.table, 2) * 100
    ##            
##               Liberal  Moderate Conservative
##   GLBCC No   6.483791 29.704797    70.644851
##   GLBCC Yes 93.516209 70.295203    29.355149

    Parece que nuestra hipótesis está apoyada, ya que hay más de un 40% de diferencia entre liberales y conservadores con moderados en el medio. Sin embargo, consideremos el chi-cuadrado antes de rechazar nuestra hipótesis nula:

    #  Chi-squared
chisq.test(v2.glbcc.table, correct = FALSE)
    ## 
##  Pearson's Chi-squared test
## 
## data:  v2.glbcc.table
## X-squared = 620.76, df = 2, p-value < 0.00000000000000022

    El chi-cuadrado es muy grande y nuestro valor p es muy pequeño. Podemos, por lo tanto, rechazar nuestra hipótesis nula con gran confianza. A continuación, consideramos la fuerza de la asociación usando V de Cramer (ya que ya sea Phi ni el coeficiente de contingencia son apropiados para una tabla de 3 X 2):

    #  Cramer's V
library(vcd)
assocstats(v2.glbcc.table)
    ##                     X^2 df P(> X^2)
## Likelihood Ratio 678.24  2        0
## Pearson          620.76  2        0
## 
## Phi-Coefficient   : NA 
## Contingency Coeff.: 0.444 
## Cramer's V        : 0.496

    El valor V de Cramer de .496 indica que tenemos una fuerte relación entre la ideología política y las creencias sobre el cambio climático.

    Sin embargo, podríamos querer considerar el género como una variable de control ya que sabemos que el género está relacionado tanto con las percepciones sobre el clima como con la ideología. Primero, necesitamos generar una nueva tabla con la variable de control género agregada. Comenzamos por factorizar la variable de género.

    #  factor the variables to add labels.
ds$f.gend <- factor(ds$gend, levels=c(0, 1), labels=c("Women", "Men"))

    Luego creamos una nueva tabla. Se muestra la salida R, en la que la línea\ #\ #,, = Mujeres indica los resultados para mujeres y\ #\ #,, = Hombres muestra los resultados para hombres.

    #  3 Two variable table glbcc~ideology+gend
v3.glbcc.table <- table(ds$f.glbcc, ds$f.ideol, ds$f.gend) 
v3.glbcc.table
    ## , ,  = Women
## 
##            
##             Liberal Moderate Conservative
##   GLBCC No       18      206          375
##   GLBCC Yes     239      470          196
## 
## , ,  = Men
## 
##            
##             Liberal Moderate Conservative
##   GLBCC No        8      116          358
##   GLBCC Yes     136      292          109
    #  Percentages by Column for Women 
prop.table(v3.glbcc.table[,,1], 2) * 100       
    ##            
##               Liberal  Moderate Conservative
##   GLBCC No   7.003891 30.473373    65.674256
##   GLBCC Yes 92.996109 69.526627    34.325744
    chisq.test(v3.glbcc.table[,,1])
    ## 
##  Pearson's Chi-squared test
## 
## data:  v3.glbcc.table[, , 1]
## X-squared = 299.39, df = 2, p-value < 0.00000000000000022
    assocstats(v3.glbcc.table[,,1])
    ##                     X^2 df P(> X^2)
## Likelihood Ratio 326.13  2        0
## Pearson          299.39  2        0
## 
## Phi-Coefficient   : NA 
## Contingency Coeff.: 0.407 
## Cramer's V        : 0.446
    #  Percentages by Column for  Men 
prop.table(v3.glbcc.table[,,2], 2) * 100    
    ##            
##               Liberal  Moderate Conservative
##   GLBCC No   5.555556 28.431373    76.659529
##   GLBCC Yes 94.444444 71.568627    23.340471
    chisq.test(v3.glbcc.table[,,2])
    ## 
##  Pearson's Chi-squared test
## 
## data:  v3.glbcc.table[, , 2]
## X-squared = 320.43, df = 2, p-value < 0.00000000000000022
    assocstats(v3.glbcc.table[,,2])
    ##                     X^2 df P(> X^2)
## Likelihood Ratio 353.24  2        0
## Pearson          320.43  2        0
## 
## Phi-Coefficient   : NA 
## Contingency Coeff.: 0.489 
## Cramer's V        : 0.561

    Tanto para hombres como para mujeres, seguimos viendo más de un 40% de diferencia y el valor p para ambas tablas chi-cuadrado es 2.2e-16 y ambas V's de Cramer son mayores a .30. Es claro que incluso cuando se controla por género, existe una relación sólida entre la ideología y el riesgo percibido de cambio climático. Sin embargo, estas tablas también sugieren que las mujeres están un poco más inclinadas a creer que los gases de efecto invernadero juegan un papel en el cambio climático que los hombres. Podemos tener una instancia de causalidad conjunta, donde tanto la ideología como el género afectan (causa” sigue siendo una palabra demasiado fuerte) opiniones sobre el impacto de los gases de efecto invernadero en el cambio climático.

    Se utilizan referencias cruzadas, chi-cuadrado y medidas de asociación con datos nominales y ordinales para proporcionar una visión general de una relación, su significancia estadística y la fuerza de una relación. En la siguiente sección, pasamos a formas de considerar el mismo conjunto de preguntas con datos de nivel de intervalo antes de pasar a la técnica más avanzada de análisis de regresión en la Parte 2 de este libro.

    This page titled 6.1: Tabulación cruzada is shared under a CC BY 4.0 license and was authored, remixed, and/or curated by Jenkins-Smith et al. (University of Oklahoma Libraries) via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.