8.1: Minimizar errores usando Derivados

En cálculo, la derivada es una medida de la pendiente de cualquier función de x, o f (x) f (x), en cada valor dado de xx. Para la función f (x) f (x), la derivada se denota como f′ (x) f′ (x) o, pronunciada como “f prime x”. Debido a que la fórmula para z22 es conocida y puede tratarse como una función, la derivada de esa función permite calcular el cambio en la suma del error cuadrado sobre cada valor posible de ^αα^ y ^ββ^. Por esa razón, necesitamos encontrar la derivada para Z22 con respecto a los cambios en ^αα^ y ^ββ^. Eso, a su vez, nos permitirá “derivar” los valores de ^αα^ y ^ββ^ que dan como resultado lo más bajo posible 22.

Miren — entendemos que todo esto suena complicado. Pero no es del todo tan complicado. En este capítulo, recorreremos todos los pasos para que veas que es realmente bastante simple y, bueno, elegante. Verá que el cálculo diferencial (el tipo de cálculo que se refiere a las tasas de cambio) se construye sobre un conjunto de reglas claramente definidas para encontrar la derivada para cualquier función f (x) f (x). Es como resolver un rompecabezas. En la siguiente sección se esbozan estas reglas, para que podamos empezar a resolver acertijos.

8.1.1 Reglas de Derivación

Reglas Derivadas

1. Regla de Poder
2. Regla Constante
3. Una constante multiplicada por una función
4. Diferenciar una suma
5. Regla del producto
6. Regla del cociente
7. Regla de Cadena

En las siguientes secciones se ofrecen ejemplos de la aplicación de cada regla.

Regla 1: La regla del poder

Ejemplo:F (x) =x6f′ (x) =6*x6−1=6x5f (x) =x6f′ (x) =6*x6−1=6x5

Un segundo ejemplo se puede trazar en R. La función es f (x) =x2f (x) =x2 y por lo tanto, usando la regla de potencia, la derivada es: f′ (x) =2xf′ (x) =2x.

x <- c(-5:5)
x

##  [1] -5 -4 -3 -2 -1  0  1  2  3  4  5

y <- x^2
y

##  [1] 25 16  9  4  1  0  1  4  9 16 25

plot(x,y, type="o", pch=19)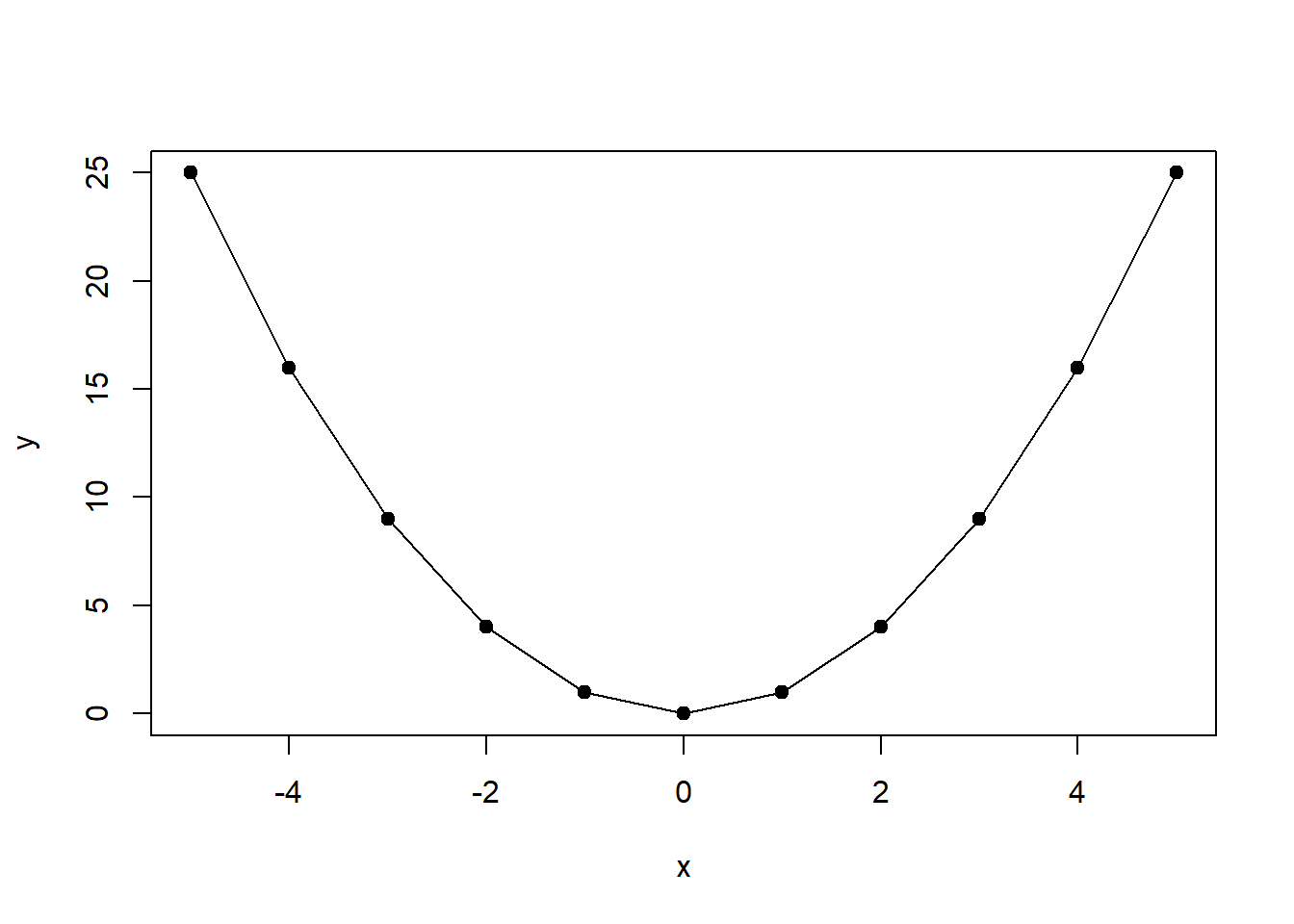

Figura\(\PageIndex{1}\): Cálculo de pendientes para pares (x, y) (x, y)

Regla 2: La regla constante

Ejemplo:F (x) =346f′ (x) =0=10xf (x) =346f′ (x) =0=10x

Regla 3: Una constante multiplicada por una función

Ejemplo:F (x) =5x2f′ (x) =5*2x2−1=10xf (x) =5x2f′ (x) =5*2x2−1=10x

Regla 4: Diferenciar una suma

Ejemplo:
f (x) =4x2+32xf′ (x) = (4x2) ′+ (32x) ′=4*2x2−1+32=8x+32f (x) =4x2+32xf′ (x) =( 4x2) ′+ (32x) ′=4*2x2−1+32=8x+32

Regla 5: La regla del producto

Ejemplo:F (x) =x3 (x−5) f′ (x) = (x3) ′ (x−5) + (x3) (x−5) ′=3x2 (x−5) + (x3) *1=3x3−15x2+x3=4x3−15x2f (x) =x3 (x−5) f′ (x) = (x3) ′ (x3) ′ (x−5) + (x3) (x−5) ′=3x2 (x−5) + (x3) *1=3x3−15x2+x3=4x3−15x2

En un segundo ejemplo, la regla del producto se aplica a la función y=f (x) =x2−6x+5y=f (x) =x2−6x+5. La derivada de esta función es f′ (x) =2x−6f′ (x) =2x−6. Esta función se puede trazar en R.

x <- c(-1:7)
x

## [1] -1  0  1  2  3  4  5  6  7

y <- x^2-6*x+5
y

## [1] 12  5  0 -3 -4 -3  0  5 12

plot(x,y, type="o", pch=19)
abline(h=0,v=0)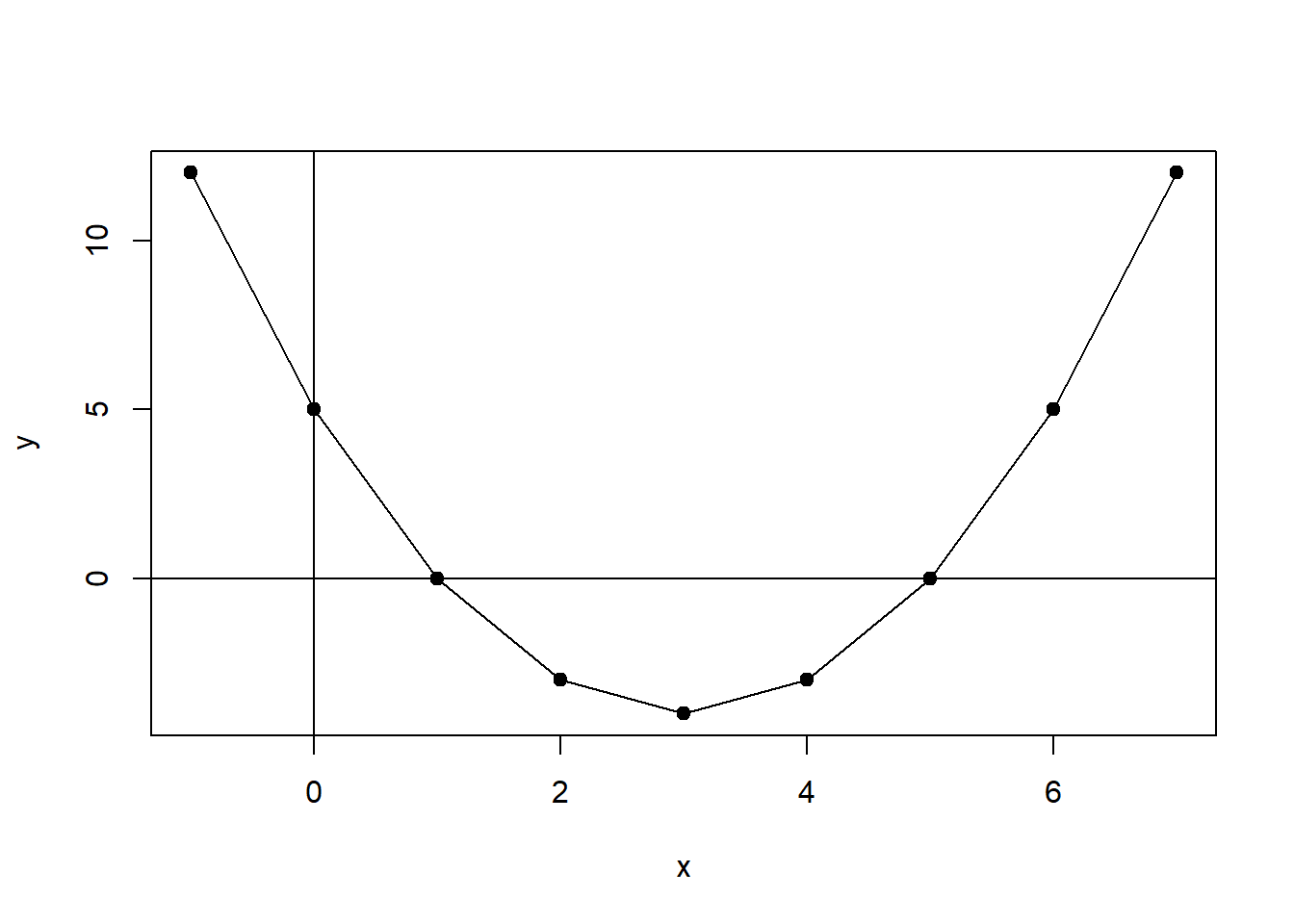

Figura\(\PageIndex{2}\): Gráfica de la función y=f (x) =x2−6x+5y=f (x) =x2−6x+5

También podemos utilizar la derivada y R para calcular la pendiente para cada valor de XX.

b <- 2*x-6
b

## [1] -8 -6 -4 -2  0  2  4  6  8

Los valores para XX, que se muestran en la Figura\(\PageIndex{2}\), van de -8 a +8 y las derivadas de retorno (pendientes en un punto) que van de -25 a +25.

Regla 6: la regla del cociente

Ejemplo:F (x) =xx2+5f′ (x) = (x2+5) (x) ′− (x2+5) ′ (x) (x2+5) 2= (x2+5) − (2x) (x) (x2+5) 2=−x2+5 (x2+5) 2f (x) =xx2+5f′ (x) = (x2+5) (x) ′− (x2+5) ′ (x) (x2+5) 2= (x2+5) − (2x) (x) (x2+5) 2=−x2+5 (x2+5) 2

Regla 7: La regla de la cadena

Ejemplo:F (x) = (7x2−2x+13) 5f′ (x) =5 (7x2−2x+13) 4∗ (7x2−2x+13) ′=5 (7x2−2x+13) 4∗ (14x−2) f (x) = (7x2−2x+13) 5f′ (x) =5 (7x2−+2x+2x+13) 5f′ (x) =5 (7x2−2x+2x+13) 4∗ (7x2−2x+13) ′=5 (7x2−2x+13) 4∗ (14x−2)

8.1.2 Puntos Críticos

Nuestro objetivo es utilizar derivados para encontrar los valores de ^αα^ y ^ββ^ que minimicen la suma del error cuadrado. Para ello necesitamos encontrar los mínimos de una función. El mínimo es el valor más pequeño que toma una función, mientras que el máximo es el valor más grande. Para encontrar los mínimos y máximos, los puntos críticos son clave. El punto crítico es donde la derivada de la función es igual a 00, o f′ (x) =0f′ (x) =0. Tenga en cuenta que esto es equivalente a la pendiente es igual a 00.

Ejemplo: Encontrar los puntos críticos

Para encontrar el punto crítico para la función

y=f (x) = (x2−4x+5) y=f (x) = (x2−4x+5);

• Primero encuentra la derivada; f′ (x) =2x−4f′ (x) =2x−4
• Establecer la derivada igual a 00; f′ (x) =2x−4=0f′ (x) =2x−4=0
• Resolver para xx; x=2x=2
• Sustituir 22 por xx en la función y resolver por yy
• Así, el punto crítico (solo hay uno en este caso) de la función es (2,1) (2,1)

Una vez identificado un punto crítico, el siguiente paso es determinar si ese punto es un mínimo o un máximo. La forma más sencilla de hacerlo es identificar las coordenadas x, y y trazar. Esto se puede hacer en R, como lo mostraremos usando la función y=f (x) =( x2−4x+5) y=f (x) =( x2−4x+5). La gráfica se muestra en la Figura\(\PageIndex{3}\).

x <- c(-5:5)
x

##  [1] -5 -4 -3 -2 -1  0  1  2  3  4  5

y <- x^2-4*x+5
y

##  [1] 50 37 26 17 10  5  2  1  2  5 10

plot(x,y, type="o", pch=19)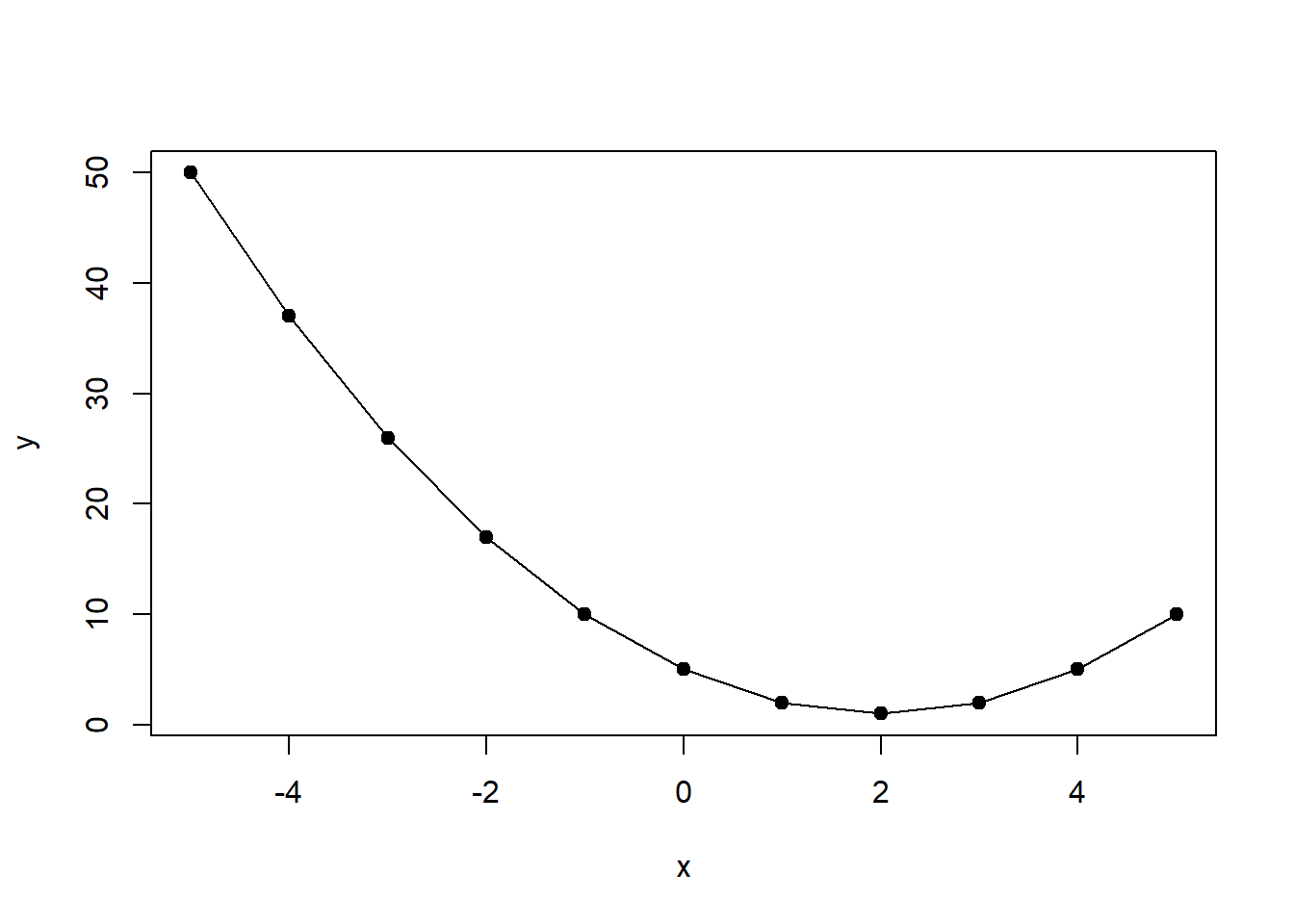

Figura\(\PageIndex{3}\): Identificación de puntos críticos

Como se puede observar, el punto crítico (2,1) (2,1) es un mínimo.

8.1.3 Derivación parcial

Cuando una ecuación incluye dos variables, una puede tomar una derivada parcial con respecto a una sola variable, mientras que la otra se trata simplemente como una constante. Esto es particularmente útil en nuestro caso porque la función z22 tiene dos variables — ^αα^ y ^ββ^.

Tomemos un ejemplo. Para la función y=f (x, z) =x3+4xz−5z2y=f (x, z) =x3+4xz−5z2, primero tomamos la derivada de xx manteniendo constante zz.

yx=f (x, z) x=3x2+4zyx=f (x, z) x=3x2+4z

A continuación tomamos la derivada de zz manteniendo la constante xx.

yz=f (x, z) z=4x−10z