8.2:8.2 Estimadores OLS derivados

Ahora que hemos desarrollado algunas de las reglas para el cálculo diferencial, podemos ver cómo OLS encuentra valores de ^αα^ y ^ββ^ que minimizan la suma del error cuadrado. En términos formales, definamos el conjunto, S (^α, ^β) S (α^, β^), como un par de estimadores de regresión que determinan conjuntamente la suma residual de cuadrados dado que: yi=^yi+i=^α+^βxi+iYI=y^i=α^i=α^^xi+i. Esta función se puede expresar:

S (^α, ^β) =ni=12i=( YI−^Yi) 2=( YI−^α−^βXI) 2S (α^, β^) =i=1ni2=( Yi−Yi^) 2=( YI−α^−β^XI) 2

Primero, derivaremos ^αα^.

8.2.1 Derivación de OLS de ^αα^

Tomar las derivadas parciales de S (^α, ^β) S (α^, β^) con respeto a (w.r.t) ^αα^ para determinar la formulación de ^αα^ que minimiza S (^α, ^β) S (α^, β^). Usando la regla de la cadena,

S (^α, ^β) ^α=2 (YI−^α−^βXI) 2−1∗ (YI−^α−^βXI) ′=e2 (YI−^α−^βXI) 1∗ (−1) =−2( YI−^α−^βXi) =−2YI+2N^α+2^βZxiS (α^, β^) α^=2 (YI−α^−β^XI) 2−1∗ (YI−α^−β^Xi) ′=Z2 (YI−α^−β^XI) 1∗ (−1) =−2( YI−α^−β^XI) =−2YI+2Nα^^Xi

A continuación, establezca la derivada igual a 00.

S (^α, ^β) ^α=−2ZYI+2N^α+2^βλxi=0S (α^, β^) α^=−2ZYI+2Nα^+2β^xi=0

Luego, desplaza los términos no-^αα^ al otro lado del signo igual:

2n^α=2ZYI−2^βXI2Nα^=2ZYI−2β^^XIPor último, dividir por 2N2n:2n^α2N=2ZYI−2^βXI2Na=IIN−^β**XI2Na=¯y−^^β¯x2Nα^2N=2YI−2β^^XI2Na=YIN=YIN=YIN=YIN=YIN=YIN−β^*xin=y¯−β^x¯^α=¯y−^β¯x (8.1) (8.1) α^=y¯−β^x¯

8.2.2 Derivación de OLS de ^ββ^

Habiendo encontrado ^αα^, el siguiente paso es derivar ^ββ^. Esta vez tomaremos la derivada parcial w.r.t ^ββ^. Como verás, los pasos son un poco más involucrados para ^ββ^ que para ^αα^.

S (^α, ^β) ^β=2 (YI−^α−^βXI) 2−1∗ (YI−^α−^βXI) ′=Z2 (YI−^α−^βXI) 1∗ (−Xi) =2( −XIYI+^αxi+^βX2i) =−2^XIYI+2^αXI+2^βXI+2^βXI+ X2is (α^, β^) β^=2 (YI−α^−β^XI) 2−1∗ (YI−α^−β^Xi) ′=Z2 (YI−α^−β^XI) 1∗ (−Xi) =2( −XIyI+α^Xi+β^Xi2) =−2α^XiYI+2α^XI+2β^XI+ ^XI2

Como sabemos que ^α=¯y−^β¯xα^=y¯−β^x¯, podemos sustituir ¯y−^β¯xy¯−β^x¯ por ^ααα^.

S (^α, ^β) ^β=−2ZxiYI+2 (¯y−^β¯x) xi+2^βλx2i=−2ZxiYI+2¯yZxi-2^β¯xI+2^βx2iS (α^, β^) β^=−2ZxiYI+2 (Y¯−β^x¯) 2XI+2β^XI2=−2XIYI+2Y¯XI−2β^x¯XI+2β^^XI+2β^XI2

A continuación, podemos sustituir YinYin por ¯YY¯ y XinXin por ¯XX¯ y establecerlo igual a 00.

S (^α, ^β) ^β=−2ZxiYI+2YIXIN−2^βXIXIXIN+2^βλx2i=0S (α^, β^) β^=−2ZxiYI+2YIXin−2β^^XI^^^^XI2=0

Luego, multiplica por n2n2 y pon todos los términos ^ββ^ del mismo lado.

N^βX2i−^β (Xi) 2=NZxiYI−XII^β (NX2i− (Xi) 2) =NZxiYI−XIYI−^^β=NZXIYI−XI−XI− (Xi) 2Nβ^^XI2−β^ (Xi) 2=NZXIYI−2I− (Xi) 2Nβ^XI−2I− ZXIIIβ ^ (NIxI2− (Xi) 2) =NIXIYI−ZXII−IIIβ ^ = NZXIYI−XII−XII− (Xi) 2

El término ^ββ^ se puede reorganizar de tal manera que:

^β=σ (Xi−¯X) (Yi−¯Y) σ (Xi−¯X) 2 (8.2) (8.2) β^=σ (Xi−X¯) (Yi−Y¯) σ (Xi−X¯) 2

Ahora recuerden lo que estamos haciendo aquí: utilizamos las derivadas parciales para 22 con respecto a ^αα^ y ^ββ^ para encontrar los valores para ^αα^ y ^ββ^ que nos darán el valor más pequeño para z22. Dicho de otra manera, las fórmulas para ^ββ^ y ^αα^ permiten el cálculo de la pendiente de minimización de errores (cambio en YY dado un cambio de una unidad en XX) e interceptar (valor para YY cuando XX es cero) para cualquier conjunto de datos que represente una relación lineal bivariada. Ninguna otra fórmula nos dará una línea, usando los mismos datos, que resulte en tan pequeño un error cuadrado. Por lo tanto, OLS se conoce como el Mejor Estimador Lineal Imsesgado (AZUL).

8.2.3 Interpretación ^ββ^ y ^αα^

En una ecuación de regresión, Y=^α+^βXY=α^+β^X, donde ^αα^ se muestra en la Ecuación (8.1) y ^ββ^ se muestra en la Ecuación (8.2). La ecuación (8.2) muestra que por cada incremento de 1 unidad en XX se obtiene ^ββ^ unidades para cambiar en YY. La ecuación (8.1) muestra que cuando XX es 00, YY es igual a ^αα^. Tenga en cuenta que en un modelo de regresión sin variables independientes, ^αα^ es simplemente el valor esperado (es decir, la media) de YY.

La intuición detrás de estas fórmulas se puede mostrar usando R para calcular “a mano” los coeficientes de pendiente (^ββ^) e interceptar (^αα^). Un modelo teórico de regresión simple se estructura de la siguiente manera:

YI=α+βXI+IYI=α+βXI+I

• αα y ββ son términos constantes
• αα es la intercepción
• ββ es la pendiente
• XiXi es un predictor de YiYi
• es el término de error

El modelo a estimar se expresa como y=^β+^βx+/epsiloni=β^+β^x+/épsilon.

Como se señaló, el objetivo es calcular el coeficiente de intercepción:

^α=¯y−^β¯xα^=y¯−β^x¯y el coeficiente de pendiente: ^β=σ (Xi−¯X) (Yi−¯Y) σ (Xi−¯X) 2β^=σ (Xi−X¯) (Yi−Y¯) σ (Xi−X¯) 2

Usando R, esto se puede lograr en unos pocos pasos. Primero, crear un vector de valores para x e y (tenga en cuenta que elegimos estos valores arbitrariamente para el propósito de este ejemplo).

x <- c(4,2,4,3,5,7,4,9)
x

## [1] 4 2 4 3 5 7 4 9

y <- c(2,1,5,3,6,4,2,7)
y

## [1] 2 1 5 3 6 4 2 7

Luego, crea objetos para ¯XX¯ y ¯YY¯:

xbar <- mean(x)
xbar

## [1] 4.75

ybar <- mean(y)
ybar

## [1] 3.75

A continuación, cree objetos para (X−¯X) (X−X¯) y (Y−¯Y) (Y−Y¯), las desviaciones de XX y YY alrededor de sus medias:

x.m.xbar <- x-xbar
x.m.xbar

## [1] -0.75 -2.75 -0.75 -1.75  0.25  2.25 -0.75  4.25

y.m.ybar <- y-ybar
y.m.ybar

## [1] -1.75 -2.75  1.25 -0.75  2.25  0.25 -1.75  3.25

Luego, calcula ^ββ^:

^β=σ (Xi−¯X) (Yi−¯Y) σ (Xi−¯X) 2β^=σ (Xi−X¯) (Yi−Y¯) σ (Xi−X¯) 2

B <- sum((x.m.xbar)*(y.m.ybar))/sum((x.m.xbar)^2)
B

## [1] 0.7183099

Finalmente, calcula ^αα^

^α=¯y−^β¯xα^=Y¯−β^x¯

A <- ybar-B*xbar
A

## [1] 0.3380282

Para ver la relación, podemos producir una gráfica de dispersión de x e y y sumar nuestra línea de regresión, como se muestra en la Figura\(\PageIndex{4}\). Entonces, por cada unidad aumenta en xx, yy aumenta en 0.7183099 y cuando xx es 00, yy es igual a 0.3380282.

plot(x,y)
lines(x,A+B*x)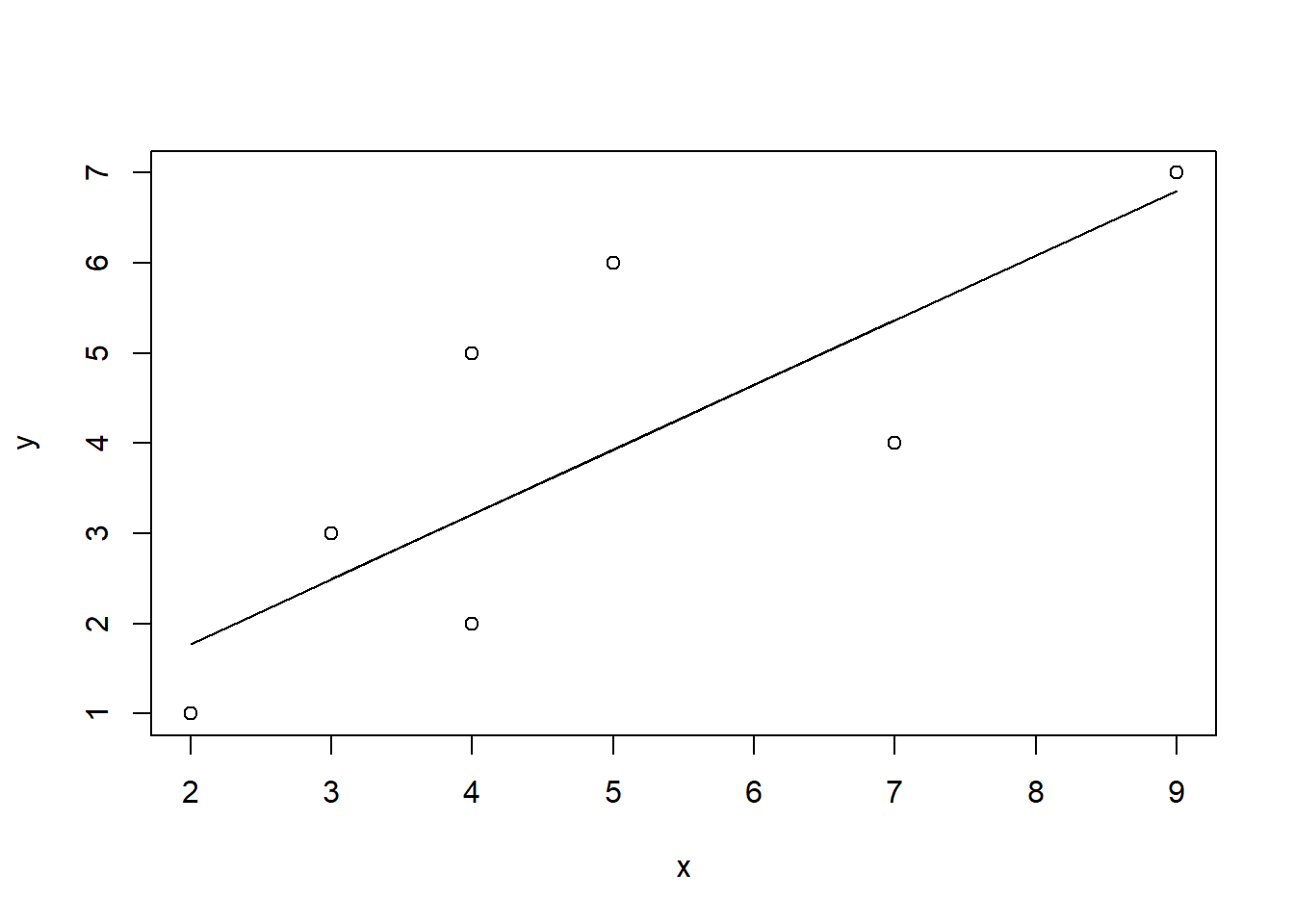

Figura\(\PageIndex{4}\): Regresión simple de xx y yy

dev.off()

## RStudioGD 
##         2