16.2: Estimación Logit
- Page ID
- 150298
Logit se utiliza cuando se predicen variables dependientes limitadas, específicamente aquellas en las que YY está representado por 00 y 11. En virtud de la variable dependiente binaria, estos modelos no cumplen con los supuestos clave de OLS. Logit utiliza estimación de máxima verosimilitud (MLE), que es una contrapartida para minimizar mínimos cuadrados. MLE identifica la probabilidad de obtener la muestra en función de los parámetros del modelo (es decir, los XX). Responde a la pregunta, ¿cuáles son los valores para BB's que hacen más probable la muestra? En otras palabras, la función de verosimilitud expresa la probabilidad de obtener los datos observados en función de los parámetros del modelo. Las estimaciones de AA y BB se basan en maximizar una función de verosimilitud de los valores YY observados.
En estimación logit buscamos P (Y=1) P (Y=1), la probabilidad de que Y=1Y=1. Las probabilidades de que Y=1Y=1 se expresan como:
\[O(Y=1)=P(Y=1)1−P(Y=1)O(Y=1)=P(Y=1)1−P(Y=1)\]
Los logits, LL, son el logaritmo natural de las probabilidades:
\[L=logeO=logeP1−PL=logeO=logeP1−P\]
Pueden variar de −∞ −∞, cuando P=0P=0, a ∞ ∞, cuando P=1P=1. LL es el componente lineal sistemático estimado:
\[L=A+B1Xi1+…+BkXikL=A+B1Xi1+…+BkXik\]
Al revertir el logit podemos obtener la probabilidad predicha de que Y=1Y=1 para cada una de las observaciones ii:
\[Pi=11−e−Li(16.2)(16.2)Pi=11−e−Li\]
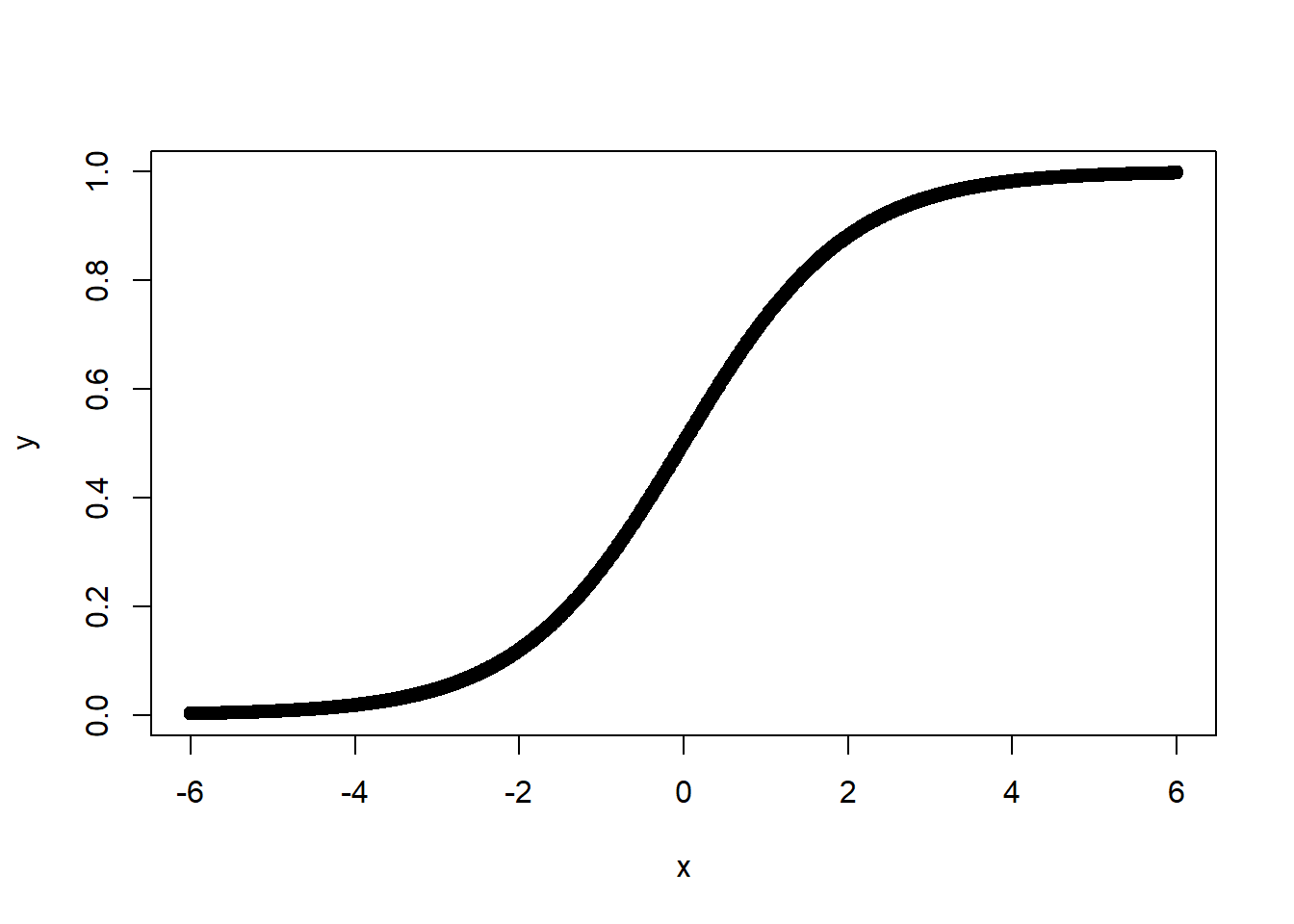
donde e=2.71828... e=2.71828..., el número base de logaritmos naturales. Tenga en cuenta que LL es una función lineal, pero PP es una función no lineal en forma de SS como se muestra en la Figura\(\PageIndex{2}\). También tenga en cuenta que la Ecuación 16.2 es la función de enlace que relaciona el componente lineal con la variable de respuesta no lineal.
En términos más formales, cada observación, ii, contribuye a la función de verosimilitud por PiPi si Yi=1Yi=1, y por 1−Pi1−Pi si Yi=0Yi=0. Esto se define como:
\[PYii(1−Pi)1−YiPiYi(1−Pi)1−Yi\]
La función de verosimilitud es el producto (multiplicación) de todas estas contribuciones individuales:
\[ℓ=∏PYii(1−Pi)1−Yiℓ=∏PiYi(1−Pi)1−Yi\]
La función de verosimilitud es la mayor para el modelo que mejor predice Y=1Y=1 o Y=0Y=0; por lo tanto, cuando el valor predicho de YY es correcto y cercano a 11 o 00, se maximiza la función de verosimilitud.
Para estimar los parámetros del modelo, buscamos maximizar el log de la función de verosimilitud. Usamos el registro porque convierte la multiplicación en suma, y por lo tanto es más fácil de calcular. La probabilidad logarítmica es:
\[logeℓ=n∑i=1[YilogePi+(1−Yi)loge(1−Pi)]logeℓ=∑i=1n[YilogePi+(1−Yi)loge(1−Pi)]\]
La solución consiste en tomar la primera derivada de la probabilidad logarítmica con respecto a cada una de las BB's, ponerlas a cero y resolver la ecuación simultánea. La solución de la ecuación no es lineal, por lo que no se puede resolver directamente. En cambio, se resuelve a través de un proceso de estimación secuencial que busca sucesivamente mejores ajustes” del modelo.
En su mayor parte, los supuestos clave requeridos para los modelos logit son análogos a los requeridos para OLS. Las diferencias clave son que (a) no asumimos una relación lineal entre los XXs y YY, y (b) no asumimos residuos homoscedastistas normalmente distribuidos. A continuación se muestran los supuestos clave que se conservan.
Supuestos Logit y Calificadores - El modelo está correctamente especificado - Las verdaderas probabilidades condicionales son función logística de los XX - No se omiten XX importantes; no se incluyen XX extraños - No se incluyen XX extraños - No hay error de medición significativo - Los casos son independientes - No XX es una función lineal de otros XX - El aumento de la multicolinealidad conduce a una mayor imprecisión - Los casos influyentes pueden sesgar estimaciones - Tamaño de la muestra: n−k−1n−k−1 debe exceder 100100 - La covariación independiente entre los XXs y YY es crítica
El siguiente ejemplo utiliza información demográfica para predecir creencias sobre el cambio climático antropogénico.
ds.temp <- ds %>%
dplyr::select(glbcc, age, education, income, ideol, gender) %>%
na.omit()
logit1 <- glm(glbcc ~ age + gender + education + income, data = ds.temp, family = binomial())
summary(logit1)##
## Call:
## glm(formula = glbcc ~ age + gender + education + income, family = binomial(),
## data = ds.temp)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.707 -1.250 0.880 1.053 1.578
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 0.4431552007 0.2344093710 1.891 0.058689 .
## age -0.0107882966 0.0031157929 -3.462 0.000535 ***
## gender -0.3131329979 0.0880376089 -3.557 0.000375 ***
## education 0.1580178789 0.0251302944 6.288 0.000000000322 ***
## income -0.0000023799 0.0000008013 -2.970 0.002977 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 3114.5 on 2281 degrees of freedom
## Residual deviance: 3047.4 on 2277 degrees of freedom
## AIC: 3057.4
##
## Number of Fisher Scoring iterations: 4Como podemos ver, la edad y el género son predictores negativos y estadísticamente significativos de la opinión sobre el cambio climático. A continuación discutimos las pruebas de hipótesis logit, bondad de ajuste y cómo interpretar los coeficientes logit.
16.2.1 Pruebas de hipótesis logit
De alguna manera, las pruebas de hipótesis con logit son bastante similares a las que utilizan OLS. Se emplea el mismo uso de valores pp; sin embargo, difieren en la forma en que se derivan. El análisis logit hace uso del estadístico Wald zz, que es similar al tt-stat en OLS. La puntuación zz de Wald compara el coeficiente estimado con el error estándar asintótico, (también conocido como la distribución normal). El valor pp se deriva de la distribución estándar asintótica normal. Cada coeficiente estimado tiene una puntuación Wald zz y un valor pp que muestra la probabilidad de que la hipótesis nula sea correcta, dados los datos.
z=BJse (Bj) (16.3) (16.3) z=BJse (Bj)
16.2.2 Bondad de ajuste
Dado que la regresión logit se estima usando MLE, los estadísticos de bondad de ajuste difieren de los de OLS. Aquí examinamos tres medidas de ajuste: log-verosimilitud, el pseudo R2R2 y los criterios de información de Akaike (AIC).
Log-verosimilitud
Para probar la hipótesis nula general de que todos los BB son iguales a cero (similar a una prueba de FF general en OLS), podemos comparar la probabilidad logarítmica del modelo demográfico con 4 IVs con el modelo nulo inicial”, que incluye solo el término de intercepción. En general, una probabilidad logarítmica menor indica un mejor ajuste. Usando el estadístico de desviación G2G2 (también conocido como el estadístico de prueba de relación de probabilidad), podemos determinar si la diferencia es estadísticamente significativa. G2G2 se expresa como:
G2=2 (Logel1−Logel0) (16.4) (16.4) G2=2 (Logel1−Logel0)
donde L1L1 es el modelo demográfico y L0L0 es el modelo nulo. El estadístico de prueba G2G2 toma la diferencia entre las probabilidades logarítmicas de los dos modelos y la compara con una distribución χ2χ2 con qq grados de libertad, donde qq es la diferencia en el número de IVs. Podemos calcular esto en R. Primero, ejecutamos un modelo nulo que predice la creencia de que los gases de efecto invernadero están causando el cambio climático, usando solo la intercepción:
logit0 <- glm(glbcc ~ 1, data = ds.temp)
summary(logit0)##
## Call:
## glm(formula = glbcc ~ 1, data = ds.temp)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -0.5732 -0.5732 0.4268 0.4268 0.4268
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.57318 0.01036 55.35 <0.0000000000000002 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for gaussian family taken to be 0.2447517)
##
## Null deviance: 558.28 on 2281 degrees of freedom
## Residual deviance: 558.28 on 2281 degrees of freedom
## AIC: 3267.1
##
## Number of Fisher Scoring iterations: 2Luego calculamos la probabilidad logarítmica para el modelo nulo,
LogEl0 (16.5) (16.5) LogEl0
logLik(logit0)## 'log Lik.' -1631.548 (df=2)A continuación, calculamos la probabilidad logarítmica para el modelo demográfico,
LogEl0 (16.6) (16.6) LogEl0
Recordemos que generamos este modelo (apodado “logit1”) antes:
logLik(logit1)## 'log Lik.' -1523.724 (df=5)Finalmente, calculamos el estadístico GG y realizamos la prueba de chi-cuadrado para significancia estadística:
G <- 2*(-1523 - (-1631))
G## [1] 216pchisq(G, df = 3, lower.tail = FALSE)## [1] 0.0000000000000000000000000000000000000000000001470144Podemos ver por el muy bajo valor p que el modelo demográfico ofrece una mejora significativa en el ajuste.
El mismo enfoque se puede utilizar para comparar modelos anidados, similares a las pruebas de FF anidadas en OLS. Por ejemplo, podemos incluir ideología en el modelo y usar la función anova para ver si la variable ideológica mejora el ajuste del modelo. Tenga en cuenta que especificamos la prueba χ2χ2.
logit2 <- glm(glbcc ~ age + gender + education + income + ideol,
family = binomial(), data = ds.temp)
summary(logit2)##
## Call:
## glm(formula = glbcc ~ age + gender + education + income + ideol,
## family = binomial(), data = ds.temp)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.6661 -0.8939 0.3427 0.8324 2.0212
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 4.0545788430 0.3210639034 12.629 < 0.0000000000000002 ***
## age -0.0042866683 0.0036304540 -1.181 0.237701
## gender -0.2044012213 0.1022959122 -1.998 0.045702 *
## education 0.1009422741 0.0293429371 3.440 0.000582 ***
## income -0.0000010425 0.0000008939 -1.166 0.243485
## ideol -0.7900118618 0.0376321895 -20.993 < 0.0000000000000002 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 3114.5 on 2281 degrees of freedom
## Residual deviance: 2404.0 on 2276 degrees of freedom
## AIC: 2416
##
## Number of Fisher Scoring iterations: 4anova(logit1, logit2, test = "Chisq")## Analysis of Deviance Table
##
## Model 1: glbcc ~ age + gender + education + income
## Model 2: glbcc ~ age + gender + education + income + ideol
## Resid. Df Resid. Dev Df Deviance Pr(>Chi)
## 1 2277 3047.4
## 2 2276 2404.0 1 643.45 < 0.00000000000000022 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Como podemos ver, sumar ideología mejora significativamente el modelo.
Pseudo R2R2
Una medida que es equivalente al R2R2 en OLS no existe para logit. Recuerda que explicar la varianza en YY no es el objetivo de MLE. Sin embargo, existe una pseudo” medida R2R2 que compara la desviación residual del modelo nulo con la del modelo completo. Al igual que la medida R2R2, el pseudo R2R2 varía de 00 a 11 con valores más cercanos a 11 que indican un ajuste mejorado del modelo.
La desviación es análoga a la suma residual de cuadrados para un modelo lineal. Se expresa como:
deviance=−2 (LogEL) (16.7) (16.7) deviance=−2 (LoGel)
Es simplemente la probabilidad logarítmica del modelo multiplicada por un −2−2. El pseudo R2R2 es 11 menos la relación de la desviación del modelo completo L1L1 a la desviación del modelo nulo L0L0:
Pseudor2=1−2 (LogEl1) −2 (LogEl0) (16.8) (16.8) Pseudor2=1−2 (LogEl1) −2 (LogEl0)
Esto se puede calcular en 'R' utilizando el modelo completo con ideología.
pseudoR2 <- 1 - (logit2$deviance/logit2$null.deviance)
pseudoR2## [1] 0.2281165El pseudo R2R2 del modelo es 0.2281165. Tenga en cuenta que el psuedo R2R2 es solo una aproximación de la varianza explicada, y debe usarse en combinación con otras medidas de ajuste como AIC.
Criterios de Información Akaike
Otra forma de examinar la bondad de ajuste es el criterio de información Akaike (AIC). Al igual que el R2R2 ajustado para OLS, el AIC toma en cuenta la parsimonia del modelo penalizando por el número de parámetros. Pero la AIC es útil sólo de manera comparativa —ya sea con el modelo nulo o con un modelo alternativo. No pretende describir el porcentaje de varianza en YY contabilizado, como lo hace el pseudo R2R2.
AIC se define como -2 veces la desviación residual del modelo más dos veces el número de parámetros, o kk IVs más la intercepción:
AIC=−2 (LoGel) +2 (k+1) (16.9) (16.9) AIC=−2 (LoGel) +2 (k+1)
Tenga en cuenta que los valores más pequeños son indicativos de un mejor ajuste. El AIC es más útil a la hora de comparar el ajuste de modelos alternativos (no necesariamente anidados). En R, el AIC se da como parte de la salida de resumen para un objeto glm, pero también podemos calcularlo y verificarlo.
aic.logit2 <- logit2$deviance + 2*6
aic.logit2## [1] 2416.002logit2$aic## [1] 2416.00216.2.3 Interpretación de Logits
Los logits, LL, son cuotas registradas y, por lo tanto, los coeficientes que se producen deben interpretarse como cuotas registradas. Esto significa que por cada unidad de cambio de ideología, las probabilidades registradas predichas de creer que el cambio climático tiene una causa antropogénica disminuye en -0.7900119. Esta interpretación, aunque matemáticamente sencilla, no es terriblemente informativa. A continuación discutimos dos formas de hacer más intuitiva la interpretación del análisis logit.
Calcular cuotas
Los logits se pueden utilizar para calcular directamente las cuotas tomando el antilog de cualquiera de los coeficientes:
Antilog=Ebantilog=EB
Por ejemplo, las siguientes retuns cuotas para todos los IV.
logit2 %>% coef() %>% exp()## (Intercept) age gender education income ideol
## 57.6608736 0.9957225 0.8151353 1.1062128 0.9999990 0.4538394Por lo tanto, por cada aumento de 1 unidad en la escala de ideología (es decir, volverse más conservador), las probabilidades de creer que el cambio climático es causado por el ser humano disminuyen en 0.4538394.
Probabilidades pronosticadas
La forma más sencilla de interpretar los logits es transformarlos en probabilidades predichas. Para calcular el efecto de una variable independiente particular, XiXi, sobre la probabilidad de Y=1Y=1, establece todos los xJxJ en sus medias, luego calcula:
^p=11+E−^LP^=11+E−l^
Luego podemos evaluar el cambio en las probabilidades pronosticadas que YY=1 a través del rango de valores en XiXi.
Este procedimiento se puede demostrar en dos etapas. Primero, crear un marco de datos que mantenga todas las variables excepto la ideología en su media. Segundo, utilizar la función de aumento para calcular las probabilidades predichas para cada nivel de ideología. Indicar type.predict = “respuesta”.
library(broom)
log.data <- data.frame(age = mean(ds.temp$age),
gender = mean(ds.temp$gender),
education = mean(ds.temp$education),
income = mean(ds.temp$income),
ideol = 1:7)
log.data <- logit2 %>%
augment(newdata = log.data, type.predict = "response")
log.data## # A tibble: 7 x 7
## age gender education income ideol .fitted .se.fit
## * <dbl> <dbl> <dbl> <dbl> <int> <dbl> <dbl>
## 1 60.1 0.412 5.09 70627. 1 0.967 0.00523
## 2 60.1 0.412 5.09 70627. 2 0.929 0.00833
## 3 60.1 0.412 5.09 70627. 3 0.856 0.0115
## 4 60.1 0.412 5.09 70627. 4 0.730 0.0127
## 5 60.1 0.412 5.09 70627. 5 0.551 0.0124
## 6 60.1 0.412 5.09 70627. 6 0.357 0.0139
## 7 60.1 0.412 5.09 70627. 7 0.202 0.0141El resultado muestra, para cada caso, la medida ideológica para el encuestado seguida de la probabilidad estimada (pp) de que el individuo cree que los gases de efecto invernadero hechos por el hombre están causando el cambio climático. También podemos graficar los resultados con intervalos de confianza 95% 95%. Esto se muestra en la Figura\(\PageIndex{3}\).
log.df <- log.data %>%
mutate(upper = .fitted + 1.96 * .se.fit,
lower = .fitted - 1.96 * .se.fit)
ggplot(log.df, aes(ideol, .fitted)) +
geom_point() +
geom_errorbar(aes(ymin = lower, ymax = upper, width = .2)) 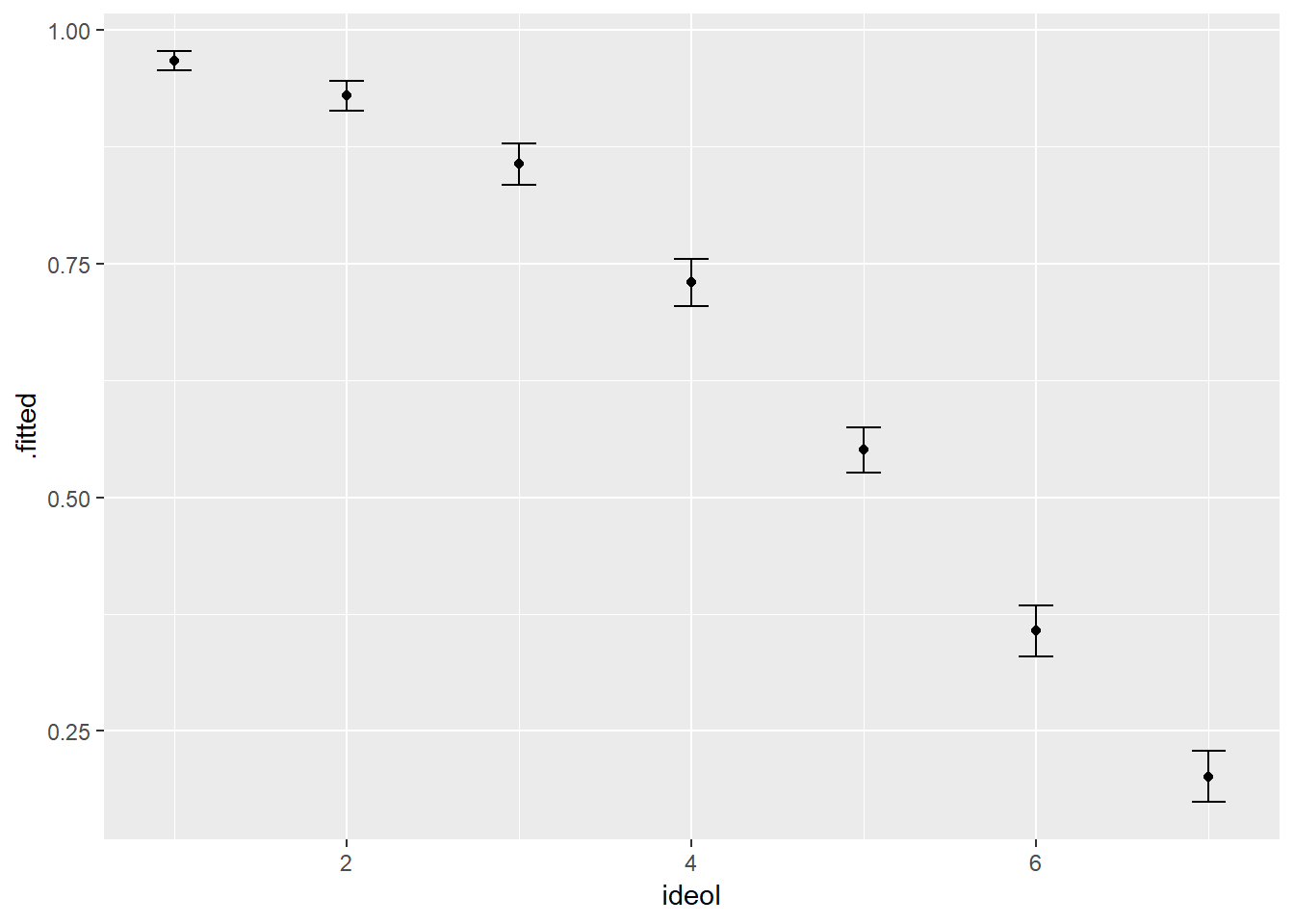
Podemos ver que a medida que los encuestados se vuelven más conservadores, la probabilidad de creer que el cambio climático es provocado por el hombre disminuye a lo que parece ser un ritmo creciente.


