3.5: Regresión — Una mini introducción
- Page ID
- 150419
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Vamos a gastar el siguiente poquito agregando una cosa más a nuestra comprensión de la correlación. Se llama regresión lineal. Suena aterrador, y realmente lo es. Te darás cuenta mucho más tarde en tu educación de Estadística que todo lo que pronto estaremos hablando puede ser pensado como un caso especial de regresión. Pero, no queremos asustarte, así que ahora mismo solo introducimos los conceptos básicos.
Primero, veamos una regresión lineal. De esta manera podemos ver lo que estamos tratando de aprender. Aquí hay algunas gráficas de dispersión, la misma que ya has visto. Pero, ¡hemos añadido algo nuevo! Líneas.
library(ggplot2)
subject_x<-1:100
chocolate_x<-round(1:100*runif(100,.5,1))
happiness_x<-round(1:100*runif(100,.5,1))
df_positive<-data.frame(subject_x,chocolate_x,happiness_x)
subject_x<-1:100
chocolate_x<-round(1:100*runif(100,.5,1))
happiness_x<-round(100:1*runif(100,.5,1))
df_negative<-data.frame(subject_x,chocolate_x,happiness_x)
subject_x<-1:100
chocolate_x<-round(runif(100,0,100))
happiness_x<-round(runif(100,0,100))
df_random<-data.frame(subject_x,chocolate_x,happiness_x)
all_data<-rbind(df_positive,df_negative,df_random)
all_data<-cbind(all_data,correlation=rep(c("positive","negative","random"),each=100))
ggplot(all_data,aes(x=chocolate_x,y=happiness_x))+
geom_point()+
theme_classic()+
geom_smooth(method="lm",se=F,formula=y ~ x)+
facet_wrap(~correlation)+
xlab("chocolate supply")+
ylab("happiness")
La mejor línea de ajuste
¿Notaste algo sobre estas líneas azules? Ojalá se pueda ver, al menos para los dos primeros paneles, que van directamente a través de los datos, al igual que un pincho de kebab. A estas líneas las llamamos líneas de mejor ajuste, porque de acuerdo a nuestra definición (pronto prometemos) no hay otras líneas que puedas dibujar que harían un mejor trabajo de ir directo a tirar los datos.
Una gran idea aquí es que estamos usando la línea como una especie de medio para describir la relación entre las dos variables. Cuando solo tenemos una variable, esa variable existe en una sola dimensión, es 1D. Entonces, es apropiado que solo tengamos un número, como la media, para describir su tendencia central. Cuando tenemos dos variables, y las trazamos juntas, ahora tenemos un espacio bidimensional. Entonces, para dos dimensiones podríamos usar una cosa más grande que es 2d, como una línea, para resumir la tendencia central de la relación entre las dos variables.
¿Qué queremos de nuestra línea? Bueno, si tuvieras un lápiz, y una impresión de los datos, podrías dibujar todo tipo de líneas rectas de la manera que quisieras. Tus líneas ni siquiera tendrían que pasar por los datos, o podrían inclinarse a través de los datos con todo tipo de ángulos. ¿Serían muy buenas todas esas líneas una descripción del patrón general de los puntos? La mayoría de ellos no lo harían. Las mejores líneas pasarían por los datos siguiendo la forma general de los puntos. De las mejores líneas, sin embargo, ¿cuál es la mejor? ¿Cómo podemos averiguarlo y a qué nos referimos con eso? En definitiva, la línea de mejor ajuste es la que tiene el menor error.
Nota
Código R para trazar residuos gracias a la entrada en el blog de Simon Jackson: https://drsimonj.svbtle.com/visualising-residuals
Echa un vistazo a esta siguiente trama, muestra una línea a través de algunos puntos. Pero, también muestra algunas líneas diminutas y diminutas. Estas líneas bajan de cada punto, y aterrizan en la línea. Cada una de estas pequeñas líneas se llama residual. Te muestran lo lejos que está la línea para diferentes puntos. Es medida de error, nos muestra lo equivocada que está la línea. Después de todo, es bastante obvio que no todos los puntos están en la línea. Esto significa que la línea no representa realmente todos los puntos. La línea está equivocada. Pero, la línea de mejor ajuste es la menos equivocada de todas las líneas equivocadas.
library(ggplot2)
d <- mtcars
fit <- lm(mpg ~ hp, data = d)
d$predicted <- predict(fit) # Save the predicted values
d$residuals <- residuals(fit) # Save the residual values
ggplot(d, aes(x = hp, y = mpg)) +
geom_smooth(method = "lm", se = FALSE,
color = "lightblue", formula=y ~ x) + # Plot regression slope
geom_segment(aes(xend = hp, yend = predicted,
color="red"), alpha = .5) + # alpha to fade lines
geom_point() +
geom_point(aes(y = predicted), shape = 1) +
theme_classic()+
theme(legend.position="none")+
xlab("X")+ylab("Y")
# Quick look at the actual, predicted, and residual values
#library(dplyr)
#d %>% select(mpg, predicted, residuals) %>% head()
Pasan muchas cosas en esta gráfica. Primero, estamos viendo un diagrama de dispersión de dos variables, una variable X e Y. Cada uno de los puntos negros son los valores reales de estas variables. Se puede ver que aquí hay una correlación negativa, a medida que X aumenta, Y tiende a disminuir. Dibujamos una línea de regresión a través de los datos, esa es la línea azul. También están estos puntitos blancos. Aquí es donde la línea piensa que deberían estar los puntos negros. Las líneas rojas son los residuos importantes de los que hemos estado hablando. Cada punto negro tiene una línea roja que cae directamente hacia abajo, o hacia arriba desde la ubicación del punto negro, y aterriza directamente sobre la línea. Ya podemos ver que muchos de los puntos no están en la línea, así que ya sabemos que la línea está “apagada” por alguna cantidad por cada punto. La línea roja solo hace que sea más fácil ver exactamente qué tan fuera de la línea está.
Lo importante que está pasando aquí, es que la línea azul que se dibuja es tal manera, que minimiza la longitud total de las líneas rojas. Por ejemplo, si quisiéramos saber qué tan equivocada estaba esta línea, simplemente podríamos juntar todas las líneas rojas, medir cuánto tiempo están y luego sumar toda la incorrección. Esto nos daría la cantidad total de maldad. Normalmente llamamos a esto el error. De hecho, ya hemos hablado de esta idea antes cuando discutimos la desviación estándar. Lo que en realidad vamos a estar haciendo con las líneas rojas, es calcular la suma de las desviaciones cuadradas de la línea. Esa suma es la cantidad total de error. Ahora bien, esta línea azul aquí minimiza la suma de las desviaciones cuadradas. Cualquier otra línea produciría un error total mayor.
Aquí hay una animación para ver esto en acción. Las animaciones comparan la línea de mejor ajuste en azul, con algunas otras posibles líneas en negro. La línea negra se mueve hacia arriba y hacia abajo. Las líneas rojas muestran el error entre la línea negra y los puntos de datos. A medida que la línea negra se mueve hacia la línea de mejor ajuste, el error total, representado visualmente por el área gris se reduce a su valor mínimo. El error total se expande a medida que la línea negra se aleja de la línea de mejor ajuste.
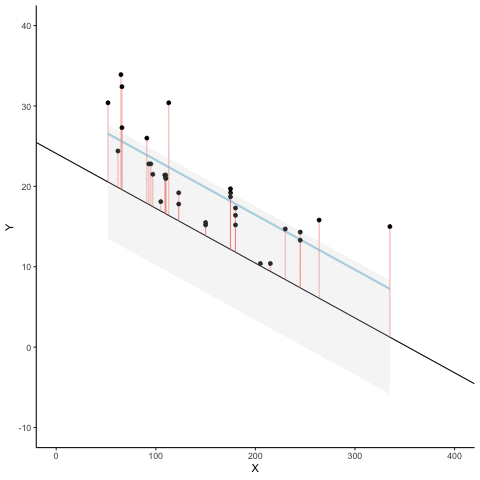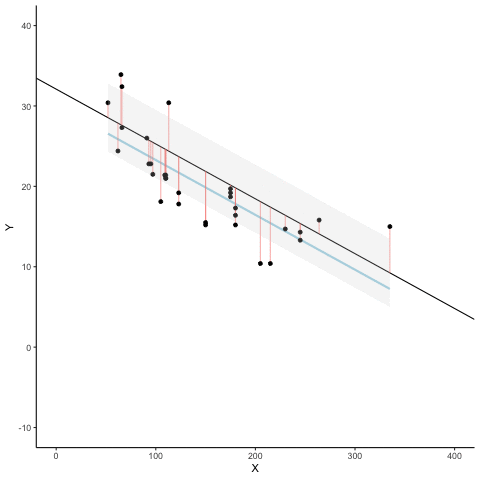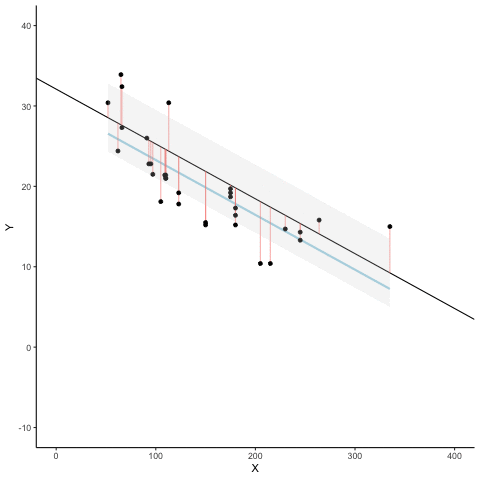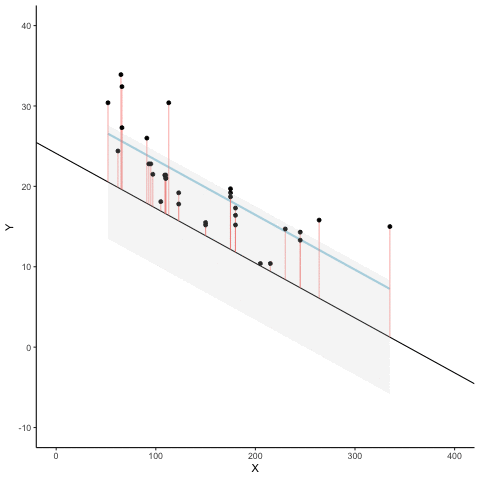
Siempre que la línea negra no se superpone con la línea azul, es peor que la línea de mejor ajuste. La línea de regresión azul es como Rcitos de Oro, es justo, y está en el medio.
Esta siguiente gráfica muestra una pequeña simulación de cómo se comporta la suma de desviaciones cuadradas (la suma de las longitudes cuadradas de las líneas rojas) a medida que movemos la línea hacia arriba y hacia abajo. Lo que está pasando aquí es que estamos calculando una medida del error total a medida que la línea negra se mueve a través de la línea de mejor ajuste. Esto representa la suma de las desviaciones cuadradas. En otras palabras, cuadramos la longitud de cada línea roja de la animación anterior, luego sumamos todas las líneas rojas cuadradas y obtenemos el error total (la suma total de las desviaciones cuadradas). El gráfico a continuación muestra cómo se ve el error total a medida que la línea negra se acerca y luego se aleja de la línea de mejor ajuste. Observe, los puntos en esta gráfica comienzan alto en el lado izquierdo, luego bajan a un mínimo en la parte inferior media de la gráfica. Al llegar a su punto mínimo, hemos encontrado una línea que minimiza el error total. Esta es la línea de regresión de mejor ajuste.
library(ggplot2)
d <- mtcars
fit <- lm(mpg ~ hp, data = d)
d$predicted <- predict(fit) # Save the predicted values
d$residuals <- residuals(fit) # Save the residual values
coefs<-coef(lm(mpg ~ hp, data = mtcars))
#coefs[1]
#coefs[2]
x<-d$hp
move_line<-seq(-5,5,.5)
total_error<-c(length(move_line))
cnt<-0
for(i in move_line){
cnt<-cnt+1
predicted_y <- coefs[2]*x + coefs[1]+i
error_y <- (predicted_y-d$mpg)^2
total_error[cnt]<-sum(error_y)
}
df<-data.frame(move_line,total_error)
ggplot(df,aes(x=move_line,y=total_error))+
geom_point()+
theme_classic()+
ylab("sum of squared deviations")+
xlab("change to y-intercept")
Bien, entonces aún no hemos hablado de la intercepción y. Pero, lo que nos muestra esta gráfica es cómo se comporta el error total a medida que movemos la línea hacia arriba y hacia abajo. El intercepto y aquí es lo que cambiamos que hace que nuestra línea se mueva hacia arriba y hacia abajo. Como puedes ver los puntos van hacia arriba cuando movemos la línea hacia abajo de 0 a -5, y los puntos suben cuando movemos la línea hacia arriba de 0 a +5. La mejor línea, que minimiza el error ocurre justo en el medio, cuando no movemos en absoluto la línea de regresión azul.
Líneas
Bien, bien dices. Entonces, hay una línea mágica que pasará por la mitad del diagrama de dispersión y minimizará la suma de las desviaciones cuadradas. ¿Cómo encuentro esta línea mágica? Te lo mostraremos. Pero, para ser completamente honesto, casi nunca lo harás de la manera que te mostraremos aquí. En cambio, es mucho más fácil usar software y hacer que tu computadora lo haga por. Aprenderás a hacerlo en los laboratorios.
Antes de mostrarte cómo encontrar la línea de regresión, vale la pena refrescar tu memoria sobre cómo funcionan las líneas, especialmente en 2 dimensiones. ¿Recuerdas esto?
\(y = ax + b\), o también\(y = mx + b\) (a veces se usa a o m para la pendiente)
Esta es la fórmula para una línea. Otra forma de escribirlo es:
\[y = slope * x + \text{y-intercept} \nonumber \]
La pendiente es la inclinación de la línea, y la intersección y es donde la línea cruza el eje y. Veamos algunas líneas:
library(ggplot2) ggplot()+ geom_abline(slope=1,intercept=5,color="blue")+ geom_abline(slope=-1, intercept=15, color="red")+ lims(x = c(1,20), y = c(0,20))+ theme_classic()
Entonces hay dos líneas. La fórmula para la línea azul es\(y = 1*x + 5\). Hablemos de eso. Cuando x = 0, ¿dónde está la línea azul en el eje y? Es a las cinco. Eso pasa porque 1 veces 0 es 0, y luego solo tenemos los cinco sobrantes. ¿Qué tal cuando x = 5? En ese caso y =10. Solo necesitas el enchufe en los números a la fórmula, así:
\[y = 1*x + 5 \nonumber \]
\[y = 1*5 + 5 = 5+5 =10 \nonumber \]
El punto de la fórmula es decirte dónde estará y, para cualquier número de x. La pendiente de la línea te indica si la línea va a subir o bajar, a medida que te mueves de izquierda a derecha. La línea azul tiene una pendiente positiva de uno, por lo que sube a medida que x sube. ¿Cuánto sube? Suba por uno para todos uno de x! Si hiciéramos la pendiente un 2, sería mucho más pronunciada, y subiéramos más rápido. La línea roja tiene una pendiente negativa, por lo que se inclinó hacia abajo. Esto significa que\(y\) va hacia abajo, como\(x\) sube. Cuando no hay inclinación, y queremos hacer una línea perfectamente plana, establecemos la pendiente en 0. Esto significa que y no va a ninguna parte ya que x se hace más y más pequeño.
Eso son líneas.
Computación de la línea de mejor ajuste
Si tiene una gráfica de dispersión que muestra las ubicaciones de las puntuaciones de dos variables, la verdadera pregunta es ¿cómo puede encontrar la pendiente y la intersección y para la línea de mejor ajuste? ¿Qué vas a hacer? Dibujar millones de líneas, sumar los residuos, y luego ver cuál era la mejor? Eso tardaría para siempre. Afortunadamente, hay computadoras, y cuando no tienes una alrededor, también hay algunas fórmulas útiles.
Nota
Vale la pena señalar lo mucho que las computadoras han cambiado todo. Antes de las computadoras todos tenían que hacer estos cálculos a mano, ¡tal tarea! Aparte de las ideas matemáticas más profundas en las fórmulas, muchas de ellas fueron hechas por conveniencia, para acelerar los cálculos manuales, porque no había computadoras. Ahora que tenemos computadoras, los cálculos de la mano suelen ser solo un ejercicio de álgebra. A lo mejor construyen carácter. Tú decides.
Te mostraremos las fórmulas. Y, trabajar a través de un ejemplo a mano. Es lo peor, lo sabemos. Por cierto, deberías sentir lástima por mí ya que hago todo esto a mano por ti.
Aquí hay dos fórmulas que podemos usar para calcular la pendiente y la intersección, directamente a partir de los datos. No vamos a entrar en por qué estas fórmulas hacen lo que hacen. Estos son para un cálculo “fácil”.
\[intercept = b = \frac{\sum{y}\sum{x^2}-\sum{x}\sum{xy}}{n\sum{x^2}-(\sum{x})^2} \nonumber \]
\[slope = m = \frac{n\sum{xy}-\sum{x}\sum{y}}{n\sum{x^2}-(\sum{x})^2} \nonumber \]
En estas fórmulas, el\(x\) y el\(y\) se refieren a las puntuaciones individuales. Aquí tienes una tabla que te muestra cómo encaja todo.
| puntajes | x | y | x_cuadrado | y_cuadrado | xy |
|---|---|---|---|---|---|
| 1 | 1 | 2 | 1 | 4 | 2 |
| 2 | 4 | 5 | 16 | 25 | 20 |
| 3 | 3 | 1 | 9 | 1 | 3 |
| 4 | 6 | 8 | 36 | 64 | 48 |
| 5 | 5 | 6 | 25 | 36 | 30 |
| 6 | 7 | 8 | 49 | 64 | 56 |
| 7 | 8 | 9 | 64 | 81 | 72 |
| Sumas | 34 | 39 | 200 | 275 | 231 |
Vemos 7 conjuntos de puntuaciones para la variable x e y. Calculamos\(x^2\) al cuadrar cada valor de x, y ponerlo en una columna. Calculamos\(y^2\) al cuadrar cada valor de y, y ponerlo en una columna. Después calculamos\(xy\), multiplicando cada\(x\) puntaje por cada\(y\) puntaje, y lo colocamos en una columna. Después agregamos todas las columnas hacia arriba, y colocamos las sumas en la parte inferior. Estos son todos los números que necesitamos para que las fórmulas encuentren la línea de mejor ajuste. Así es como se ven las fórmulas cuando ponemos números en ellas:
\[intercept = b = \frac{\sum{y}\sum{x^2}-\sum{x}\sum{xy}}{n\sum{x^2}-(\sum{x})^2} = \frac{39 * 200 - 34*231}{7*200-34^2} = -.221 \nonumber \]
\[slope = m = \frac{n\sum{xy}-\sum{x}\sum{y}}{n\sum{x^2}-(\sum{x})^2} = \frac{7*231-34*39}{7*275-34^2} = 1.19 \nonumber \]
Genial, ahora podemos comprobar nuestro trabajo, trazemos las puntuaciones en un diagrama de dispersión y dibujemos una línea a través de él con pendiente = 1.19, y una intersección en y de -.221. Debe pasar por la mitad de los puntos.
library(ggplot2) x<-c(1,4,3,6,5,7,8) y<-c(2,5,1,8,6,8,9) plot_df<-data.frame(x,y) ggplot(plot_df,aes(x=x,y=y))+ geom_point()+ geom_smooth(method="lm",se=FALSE, formula=y ~ x)+ theme_classic()
