3.6: Interpretación de correlaciones
- Page ID
- 150412
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
¿Qué significa la presencia o ausencia de correlación entre dos medidas? ¿Cómo deben interpretarse las correlaciones? ¿Qué tipo de inferencias se pueden extraer de las correlaciones? Estas son todas muy buenas preguntas. Un primer consejo es tener precaución a la hora de interpretar las correlaciones. He aquí por qué.
La correlación no es igual a causalidad
A lo mejor usted ha escuchado que la correlación no equivale a causalidad. ¿Por qué no? Hay muchas razones por las que no. No obstante, antes de enumerar algunas de las razones comencemos con un caso en el que esperaríamos una conexión causal entre dos mediciones. Considera, comprar una planta de serpiente para tu hogar. Se supone que las plantas de serpiente son fáciles de cuidar porque en su mayoría puedes ignorarlas.
Como la mayoría de las plantas, las plantas de serpiente necesitan algo de agua para mantenerse con vida Sin embargo, también necesitan la cantidad justa de agua. Imagina un experimento donde se cultivaron 1000 plantas de serpiente en una casa. A cada planta de serpiente se le da una cantidad diferente de agua por día, desde cero cucharaditas de agua por día hasta 1000 cucharaditas de agua por día. Supondremos que el agua es parte del proceso causal que permite que las plantas de serpiente crezcan. La cantidad de agua que se da a cada planta de serpiente por día también puede ser una de nuestras medidas. Imagínese además que cada semana el experimentador mide el crecimiento de las plantas de serpiente, que será la segunda medida. Ahora, ¿te imaginas por ti mismo cómo sería un diagrama de dispersión de crecimiento semanal de plantas de serpiente por cucharadas de agua?
Incluso cuando hay causalidad, puede que no haya correlación obvia
La primera planta a la que no se le diera agua en absoluto la pasaría muy mal y eventualmente moriría. Debe tener la menor cantidad de crecimiento semanal. ¿Qué tal las plantas a las que se les da solo unas cucharaditas de agua al día? Esta podría ser el agua suficiente para mantener vivas las plantas, así que crecerán un poco pero no mucho. Si estás imaginando un diagrama de dispersión, con cada punto siendo una planta serpiente, entonces deberías imaginar algunos puntos comenzando en la esquina inferior izquierda (sin agua y sin crecimiento de plantas), moviéndose hacia arriba y hacia la derecha (un poco de agua, y un poco de crecimiento). Al observar que las plantas de serpiente reciben cada vez más agua, deberíamos ver cada vez más crecimiento de las plantas, ¿verdad? “Claro, pero sólo hasta cierto punto”. Correcto, debe haber una tendencia a una correlación positiva con el aumento del crecimiento de las plantas a medida que aumenta la cantidad de agua por día. Pero, ¿qué pasa cuando le das demasiada agua a las plantas de serpiente? Por experiencia personal, mueren. Entonces, en algún momento, los puntos en la gráfica de dispersión comenzarán a moverse de nuevo hacia abajo. Las plantas de serpiente que reciben demasiada agua no crecerán muy bien.
La gráfica de dispersión imaginaria que deberías estar imaginando podría tener una forma de U al alza. Pasando de izquierda a derecha, los puntos suben, alcanzan un máximo, luego vuelven a bajar llegando a un mínimo. Computar Pearson\(r\) para datos como este puede darte\(r\) valores cercanos a cero. El diagrama de dispersión podría verse así:
library(ggplot2)
water<-seq(0,999,1)
growth<-c(seq(0,10,(10/499)),seq(10,0,-(10/499)))
noise<-runif(1000,-2,2)
growth<-growth+noise
snake_df<-data.frame(growth,water)
ggplot(snake_df, aes(x=water,y=growth))+
geom_point()+
theme_classic()+
xlab("Water (teaspoons)")+
ggtitle("Imaginary snake plant growth \n as a function of water")
Concedido esto se parece más a una V invertida, que a una U invertida, pero ¿entiendes bien la imagen? Claramente existe una relación entre el riego y el crecimiento de las plantas de serpiente. Pero, la correlación no va en una dirección. Como resultado, cuando calculamos la correlación en términos de r de Pearson, obtenemos un valor que sugiere que no hay relación.
Lo que esto realmente significa es que no existe una relación lineal que pueda describirse con una sola línea recta. Cuando necesitamos líneas o curvas que vayan en más de una dirección, tenemos una relación no lineal.
Este ejemplo ilustra algunos acertijos en la interpretación de correlaciones. Ya sabemos que se necesita agua para que las plantas crezcan, por lo que, con razón, esperamos que haya una relación entre nuestra medida de cantidad de agua y el crecimiento de las plantas. Si miramos la primera mitad de los datos vemos una correlación positiva, si miramos la última mitad de los datos vemos una correlación negativa, y si miramos todos los datos no vemos correlación. ¡Ay! Entonces, incluso cuando hay una conexión causal entre dos medidas, no necesariamente obtendremos evidencia clara de la conexión con solo calcular un coeficiente de correlación.
Consejo profesional: Esta es una de las razones por las que trazar tus datos es tan importante. Si ves un patrón en forma de U al alza, entonces un análisis de correlación probablemente no sea el mejor análisis para tus datos.
Variable de confusión o problema de tercera variable
Cualquiera puede correlacionar dos cosas cualesquiera que puedan cuantificarse y medirse. Por ejemplo, podríamos encontrar a cien personas, hacerles todo tipo de preguntas como:
- que tan feliz eres
- cuántos años tienes
- qué tan alto eres
- cuánto dinero ganas al año
- cuanto largas son tus pestañas
- cuantos libros has leído en tu vida
- qué tan fuerte es tu voz interior
Digamos que encontramos una correlación positiva entre el salario anual y la felicidad. Tenga en cuenta que podríamos haber calculado con la misma facilidad la misma correlación entre la felicidad y el salario anual. Si encontramos una correlación, ¿estarías dispuesto a inferir que el salario anual causa felicidad? Quizás sí juega un pequeño papel. Pero, algo así como la felicidad probablemente tiene muchas causas contribuyentes. El dinero podría hacer directamente que algunas personas sean felices. Pero, lo más probable es que el dinero compre a la gente el acceso a todo tipo de cosas, y algunas de esas cosas podrían contribuir a la felicidad. Estas “otras” cosas se llaman terceras variables. Por ejemplo, quizás las personas que viven en lugares más agradables en casas más caras son más felices que las personas en peores lugares en casas más baratas. En este escenario, el dinero no está causando felicidad, son los lugares y casas que compra el dinero. Pero, incluso si esto fuera cierto, la gente todavía puede ser más o menos feliz en muchas situaciones diferentes.
La lección aquí es que se puede producir una correlación entre dos medidas debido a una tercera variable que no se mide directamente. Entonces, solo porque encontremos una correlación, no significa que podamos concluir nada sobre una conexión causal entre dos mediciones.
Correlación y azar aleatorio
Otro aspecto muy importante de las correlaciones es el hecho de que se pueden producir por casualidad aleatoria. Esto significa que se puede encontrar una correlación positiva o negativa entre dos medidas, incluso cuando no tienen absolutamente nada que ver entre sí. Podría haber esperado encontrar correlación cero cuando dos medidas no están totalmente relacionadas entre sí. Aunque esto ciertamente sucede, medidas no relacionadas pueden producir accidentalmente correlaciones espurias, solo por casualidad.
Demostremos cómo las correlaciones pueden ocurrir por casualidad cuando no hay conexión causal entre dos medidas. Imagina a dos participantes. Uno está en el polo Norte con una máquina de lotería llena de bolas con números del 1 al 10. El otro está en el polo sur con una máquina de lotería diferente llena de bolas con números del 1 al 10. Hay un suministro interminable de bolas en la máquina, por lo que cada número podría ser recogido para cualquier bola. Cada participante elige al azar 10 bolas, luego registra el número en la pelota. En esta situación asumiremos que no hay manera posible de que las bolas elegidas por el primer participante puedan influir causalmente en las bolas elegidas por el segundo participante. Están del otro lado del mundo. Debemos asumir que las bolas serán elegidas solo por casualidad.
Así es como podrían verse los números de cada bola para cada participante:
| Pelota | Polo Norte | Polo Sur |
|---|---|---|
| 1 | 3 | 1 |
| 2 | 7 | 7 |
| 3 | 8 | 8 |
| 4 | 6 | 9 |
| 5 | 4 | 6 |
| 6 | 10 | 10 |
| 7 | 2 | 2 |
| 8 | 5 | 8 |
| 9 | 2 | 5 |
| 10 | 2 | 3 |
En este caso, si calculáramos los de Pearson\(r\), encontraríamos que\(r = \)
Pero, ya sabemos que este valor no nos dice nada sobre la relación entre las bolas elegidas en el polo norte y sur. Sabemos que la relación debe ser completamente aleatoria, porque así es como configuramos el juego.
La mejor pregunta aquí es preguntar ¿qué puede hacer el azar aleatorio? Por ejemplo, si corriéramos nuestro juego una y otra vez miles de veces, cada vez eligiendo nuevas bolas, y cada vez calculando la correlación, ¿qué encontraríamos? Primero, encontraremos fluctuación. El valor r a veces será positivo, a veces negativo, a veces será grande y a veces pequeño. Segundo, veremos cómo se ve la fluctuación. Esto nos dará una ventana a los tipos de correlaciones que solo el azar puede producir. Veamos qué pasa.
Simulación monte-carlo de correlaciones aleatorias
Es posible utilizar una computadora para simular nuestro juego tantas veces como queramos. Este proceso a menudo se denomina simulación monte-carlo.
A continuación se muestra un guión escrito para el lenguaje de programación R. Aquí no entraremos en los detalles del código. No obstante, expliquemos brevemente lo que está pasando. Observe, la parte que dice por (sim en 1:1000). Esto crea un bucle que repite nuestro juego 1000 veces. Dentro del bucle hay variables llamadas North_pole y South_pole. Durante cada simulación, se muestrea 10 números aleatorios (entre 1 y 10) en cada variable. Estos números aleatorios representan los números que habrían estado en las bolas de la máquina de lotería. Una vez que tenemos 10 números aleatorios para cada uno, luego calculamos la correlación usando cor (North_pole, South_pole). Luego, guardamos el valor de correlación y pasamos a la siguiente simulación. Al final, tendremos 1000\( r \) valores individuales de Pearson.
library(ggplot2)
simulated_correlations <- length(0)
for(sim in 1:1000){
North_pole <- runif(10,1,10)
South_pole <- runif(10,1,10)
simulated_correlations[sim] <- cor(North_pole,South_pole)
}
sim_df <- data.frame(sims=1:1000,simulated_correlations)
ggplot(sim_df, aes(x = sims, y = simulated_correlations))+
geom_point()+
theme_classic()+
geom_hline(yintercept = -1)+
geom_hline(yintercept = 1)+
ggtitle("Simulation of 1000 r values")
Echemos un vistazo a todos los\(r\) valores de 1000 Pearson. ¿Te resulta familiar la siguiente figura? Debería, ya hemos realizado un tipo similar de simulación antes. Cada punto en la gráfica de dispersión muestra el Pearson\(r\) para cada simulación de 1 a 1000. Como puede ver los puntos están por todo el lugar, entre el rango -1 a 1. La lección importante aquí es que el azar azar produjo todas estas correlaciones. Esto significa que podemos encontrar “correlaciones” en los datos que carecen completamente de sentido, y no reflejan ninguna relación causal entre una medida y otra.
Ilustremos la idea de encontrar correlaciones “aleatorias” una vez más, con una pequeña película. Esta vez, te mostraremos un diagrama de dispersión de los valores aleatorios muestreados para las bolas elegidas del polo Norte y Sur. Si no hay relación deberíamos ver puntos yendo a todas partes. Si sucede que hay una relación positiva (puramente por casualidad), deberíamos ver los puntos yendo de abajo a la izquierda a la parte superior derecha. Si sucede que hay una relación negativa (puramente por casualidad), deberíamos ver los puntos yendo de arriba a la izquierda hacia abajo hacia abajo a la derecha.
En más cosa para prepararte para la película. Hay tres diagramas de dispersión a continuación, que muestran correlaciones negativas, positivas y cero entre dos variables. Ya has visto esta gráfica antes. Solo te estamos recordando que las líneas azules son útiles para ver la correlación.Las correlaciones negativas ocurren cuando una línea baja de arriba a la izquierda a abajo derecha. Las correlaciones positivas ocurren cuando una línea sube desde la parte inferior izquierda hasta la parte superior derecha. Las correlaciones cero ocurren cuando la línea es plana (no sube ni baja).
library(ggplot2)
subject_x<-1:100
chocolate_x<-round(1:100*runif(100,.5,1))
happiness_x<-round(1:100*runif(100,.5,1))
df_positive<-data.frame(subject_x,chocolate_x,happiness_x)
subject_x<-1:100
chocolate_x<-round(1:100*runif(100,.5,1))
happiness_x<-round(100:1*runif(100,.5,1))
df_negative<-data.frame(subject_x,chocolate_x,happiness_x)
subject_x<-1:100
chocolate_x<-round(runif(100,0,100))
happiness_x<-round(runif(100,0,100))
df_random<-data.frame(subject_x,chocolate_x,happiness_x)
all_data<-rbind(df_positive,df_negative,df_random)
all_data<-cbind(all_data,correlation=rep(c("positive","negative","random"),each=100))
ggplot(all_data,aes(x=chocolate_x,y=happiness_x))+
geom_point()+
geom_smooth(method=lm,se=FALSE, formula=y ~ x)+
theme_classic()+
facet_wrap(~correlation)+
xlab("chocolate supply")+
ylab("happiness")
Bien, ahora ya estamos listos para la película. Está viendo el proceso de muestreo de dos conjuntos de números al azar, uno para la variable X y otro para la variable Y. Cada vez que tomamos muestras de 10 números para cada uno, los trazamos, luego dibujamos una línea a través de ellos. Recuerde, estos números son todos completamente aleatorios, por lo que debemos esperar, en promedio, que no debe haber correlación entre los números. Sin embargo, esto no es lo que sucede. Puedes la línea que va por todo el lugar. A veces encontramos una correlación negativa (la línea baja), a veces vemos una correlación positiva (la línea sube), y a veces parece correlación cero (la línea es más plana).
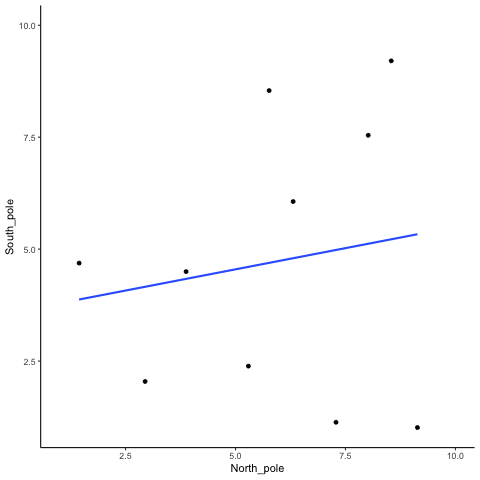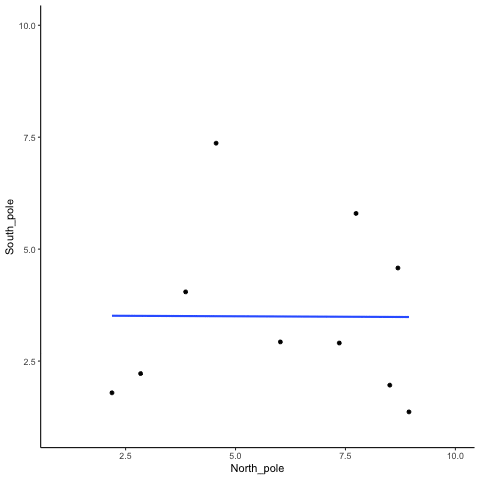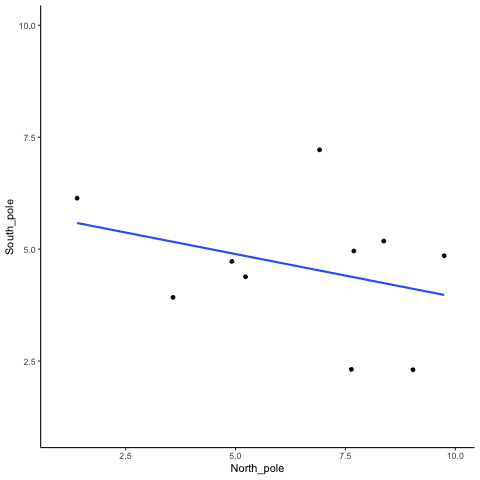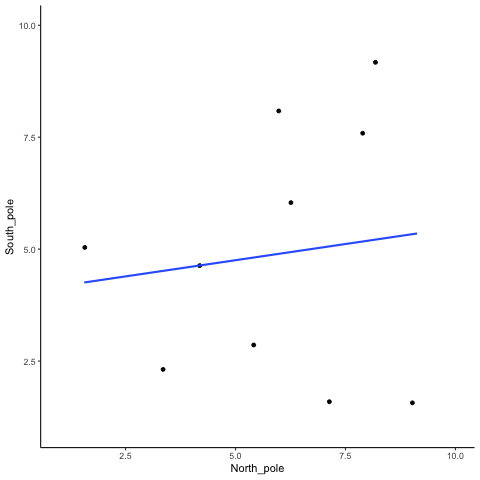
Podrías estar pensando que esto es algo perturbador. Si sabemos que no debe haber correlación entre dos variables aleatorias, ¿cómo es que estamos encontrando correlaciones? Este es un gran problema ¿verdad? O sea, si alguien me mostrara una correlación entre dos cosas, y luego afirmara que una cosa estaba relacionada con otra, cómo podría saber yo si era verdad. Después de todo, ¡podría ser casualidad! El azar también puede hacer eso.
Afortunadamente, no todo está perdido. Podemos mirar nuestros datos simulados de otra manera, usando un histograma. Recuerda, justo antes de la película, simulamos 1000 correlaciones diferentes usando números aleatorios. Al poner todos esos\( r \) valores en un histograma, podemos tener una mejor idea de cómo se comporta el azar. Podemos ver qué tipo de correlaciones es probable o poco probable que produzca el azar. Aquí hay un histograma de los\( r \) valores simulados.
simulated_correlations <- length(0)
for(sim in 1:1000){
North_pole <- runif(10,1,10)
South_pole <- runif(10,1,10)
simulated_correlations[sim] <- cor(North_pole,South_pole)
}
hist(simulated_correlations,breaks=seq(-1,1,.1))
Observe que este histograma no es plano. La mayoría de los\(r\) valores simulados son cercanos a cero. Observe, también que las barras se hacen más pequeñas a medida que se aleja de cero en la dirección positiva o negativa. Lo general para llevar a casa aquí es que el azar puede producir una amplia gama de correlaciones. Sin embargo, no todas las correlaciones ocurren muy a menudo. Por ejemplo, las barras para -1 y 1 son muy pequeñas. El azar no produce correlaciones casi perfectas muy a menudo. Las barras alrededor de -.5 y .5 son más pequeñas que las barras alrededor de cero, ya que las correlaciones medias no ocurren tan a menudo como pequeñas correlaciones solo por casualidad.
Se puede pensar en este histograma como la ventana de oportunidad. Muestra lo que suele hacer el azar, y lo que muchas veces no hace. Si encontró una correlación bajo estas mismas circunstancias (por ejemplo, midió la correlación entre dos conjuntos de 10 números aleatorios), entonces podría consultar esta ventana. ¿Qué deberías preguntar a la ventana? ¿Qué tal, podría haber venido de esta ventana mi correlación observada (la que encontraste en tus datos)? Digamos que encontraste una correlación de\(r = .1\). ¿Podría haber salido un .1 del histograma? Bueno, mira el histograma alrededor de donde está la marca .1 en el eje x. ¿Hay un bar grande ahí? Si es así, esto significa que el azar produce este valor con bastante frecuencia. Podrías sentirte cómodo con la inferencia: Sí, este .1 podría haberse producido por casualidad, porque está bien dentro de la ventana del azar. ¿Qué tal\(r = .5\)? El bar es mucho más pequeño aquí, se podría pensar, “bueno, puedo ver que el azar produce .5 algunas veces, así que el azar podría haber producido mi .5. ¿Lo hizo? Tal vez, tal vez no, no estoy seguro”. Aquí, su confianza en una fuerte inferencia sobre el papel del azar podría comenzar a ponerse un poco más temblorosa.
¿Qué tal un\(r = .95\)?. Puede que veas que el listón para .95 es muy muy pequeño, quizás demasiado pequeño para verlo. ¿Qué te dice esto? Te dice que el azar no produce .95 muy a menudo, apenas si lo hace, prácticamente nunca. Entonces, si encontraras un .95 en tus datos, ¿qué inferirías? Quizás te sentirías cómodo inferir que el azar no produjo tu .95, después de que .95 está mayormente fuera de la ventana del azar.
Aumentar el tamaño de la muestra disminuye la oportunidad de correlación espuria
Antes de seguir adelante, hagamos una cosa más con las correlaciones. En nuestro juego de lotería simulada, cada participante solo probó 10 bolas cada una. Encontramos que esto podría conducir a un rango de correlaciones entre los números sorteados aleatoriamente de cualquiera de los lados del polo. En efecto, incluso encontramos algunas correlaciones que eran de tamaño mediano a grande. Si usted fuera un investigador que encontró tales correlaciones, podría sentirse tentado a creer que había una relación entre sus medidas. No obstante, sabemos en nuestro pequeño juego, que esas correlaciones serían espurias, sólo un producto de muestreo aleatorio.
La buena noticia es que, como investigador, se llega a hacer las reglas del juego. Se llega a determinar cómo puede jugar el azar. Todo esto es un poco metafórico, así que vamos a hacerlo concreto.
Veremos qué sucede en cuatro escenarios diferentes. Primero, vamos a repetir lo que ya hicimos. Cada participante dibujará 10 bolas, luego calculamos la correlación, y lo haremos más de 1000 veces y miraremos un histograma. Segundo, cambiaremos el juego para que cada participante dibuje 50 bolas cada una, para luego repetir nuestra simulación. Tercero, y cuarto, cambiaremos el juego para que cada participante dibuje 100 bolas cada una, y luego 1000 bolas cada una, y repita etc.
La gráfica siguiente muestra cuatro histogramas diferentes de los\(r\) valores de Pearson en cada uno de los diferentes escenarios. Cada escenario involucra un tamaño de muestra diferente, de, 10, 50, 100 a 1000.
library(ggplot2)
all_df<-data.frame()
for(s_size in c(10,50,100,1000)){
simulated_correlations <- length(0)
for(sim in 1:1000){
North_pole <- runif(s_size,1,10)
South_pole <- runif(s_size,1,10)
simulated_correlations[sim] <- cor(North_pole,South_pole)
}
sim_df <- data.frame(sample_size=rep(s_size,1000),sims=1:1000,simulated_correlations)
all_df<-rbind(all_df,sim_df)
}
ggplot(all_df,aes(x=simulated_correlations))+
geom_histogram(bins=30)+
facet_wrap(~sample_size)+
theme_classic()
Al inspeccionar los cuatro histogramas se debe notar un patrón claro. El ancho o rango de cada histograma se reduce a medida que aumenta el tamaño de la muestra. ¿Qué está pasando aquí? Bueno, ya sabemos que podemos pensar en estos histogramas como ventanas de azar. Nos dicen qué\(r\) valores ocurren con bastante frecuencia, cuáles no. Cuando nuestro tamaño de muestra es 10, ocurren muchos\(r\) valores diferentes. Ese histograma es muy plano y extendido. Sin embargo, a medida que aumenta el tamaño de la muestra, vemos que se tira de la ventana de oportunidad. Por ejemplo, para cuando lleguemos a 1000 bolas cada una, casi todos los\(r\) valores de Pearson están muy cerca de 0.
Uno que se lleva a casa aquí, es que aumentar el tamaño de la muestra estrecha la ventana de oportunidad. Entonces, por ejemplo, si ejecutó un estudio que involucra 1000 muestras de dos medidas, y encontró una correlación de .5, entonces puede ver claramente en el histograma inferior derecho que .5 no ocurre muy a menudo solo por casualidad. De hecho, no hay barra, porque no sucedió ni una sola vez en la simulación. Como resultado, cuando tienes un tamaño de muestra grande como n = 1000, podrías estar más seguro de que tu correlación observada (digamos de .5) no era una correlación espuria. Si el azar no está produciendo tu resultado, entonces algo más lo es.
Por último, observe cómo su confianza sobre si el azar está molestando o no con sus resultados depende del tamaño de su muestra. Si solo obtuviste 10 muestras por medida, y las encontraste\( r = .5 \), no debes estar tan seguro de que tu correlación refleja una relación real. En cambio, se puede ver que\( r \) eso de .5 sucede bastante a menudo solo por casualidad.
Consejo profesional: cuando ejecutas un experimento puedes decidir cuántas muestras recogerás, lo que significa que puedes elegir estrechar la ventana de oportunidad. Entonces, si encuentras una relación en los datos puedes estar más seguro de que tu hallazgo es real, y no solo algo que sucedió por casualidad.
Algunas películas más
Vamos a inculcar esta idea con algunas películas más. Cuando nuestro tamaño de muestra es pequeño (N es pequeño), el error de muestreo puede causar todos los “patrones” de clasificación en los datos. Esto hace posible, y de hecho común, que se produzcan “correlaciones” entre dos conjuntos de números. Cuando aumentamos el tamaño de la muestra, se reduce el error de muestreo, lo que hace que sea menos posible que las “correlaciones” ocurran solo por casualidad. Cuando N es grande, el azar tiene menos oportunidad de operar.
Observando cómo se comporta la correlación cuando no hay correlación
A continuación, mostramos aleatoriamente números para dos variables, los trazamos y mostramos la correlación usando una línea. Hay cuatro paneles, cada uno mostrando el número de observaciones en las muestras, de 10, 50, 100, a 1000 en cada muestra.
Recuerde, debido a que estamos muestreando aleatoriamente números, no debe haber relación entre las variables X e Y. Pero, como hemos estado discutiendo, por casualidad, a veces podemos observar una correlación (por casualidad). Lo importante a observar es cómo se comporta la línea a través de los cuatro paneles. La línea gira alrededor en todas las direcciones cuando el tamaño de la muestra es 10. También se mueve bastante cuando el tamaño de la muestra es de 50 o 100. Todavía se mueve un poco cuando el tamaño de la muestra es 1000, pero mucho menos. En todos los casos esperamos que la línea sea plana, pero cada vez que tomamos nuevas muestras, a veces la línea nos muestra pseudo patrones.
¿En qué línea deberías confiar? Bueno, ojalá se pueda ver que la línea para 1000 muestras es la más estable. Tiende a ser muy plano cada vez, y no depende tanto de la muestra en particular. La línea con 10 observaciones por muestra recorre todo el lugar. El llevar a casa aquí, es que si alguien te dijo que encontró una correlación, deberías querer saber cuántas observaciones entregan en su muestra. Si solo tuvieran 10 observaciones, ¿cómo podría confiar en la afirmación de que había una correlación? ¡¡¡¡¡¡¡No puedes! No ahora que conoces muestras que son tan pequeñas pueden hacer todo tipo de cosas solo por casualidad. Si en cambio, descubriste que la muestra era muy grande, entonces podrías confiar en que encontrar un poco más. Por ejemplo, en la película anterior se puede ver que cuando hay 1000 muestras, nunca vemos una correlación fuerte o débil; la línea siempre es plana. Esto se debe a que el azar casi nunca produce correlaciones fuertes cuando el tamaño de la muestra es muy grande.
En el ejemplo anterior, muestreamos números aleatorios de una distribución uniforme. Muchos ejemplos de datos del mundo real vendrán de una distribución normal o aproximadamente normal. Podemos repetir lo anterior, pero muestrear números aleatorios de la misma distribución normal. Todavía habrá cero correlación real entre las variables X e Y, porque todo se muestrea aleatoriamente. Pero, seguimos viendo el mismo comportamiento que el anterior. La correlación calculada para tamaños de muestra pequeños fluctúa salvajemente, y los tamaños de muestra grandes no.
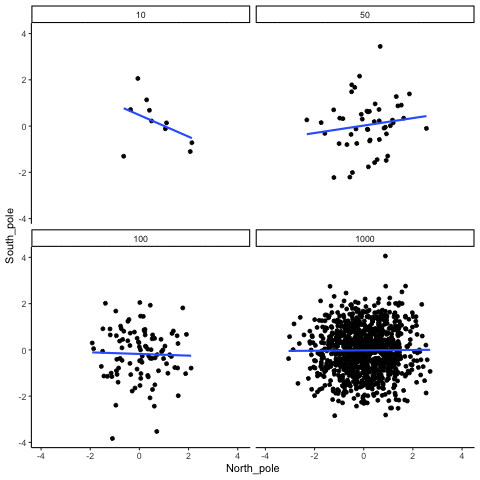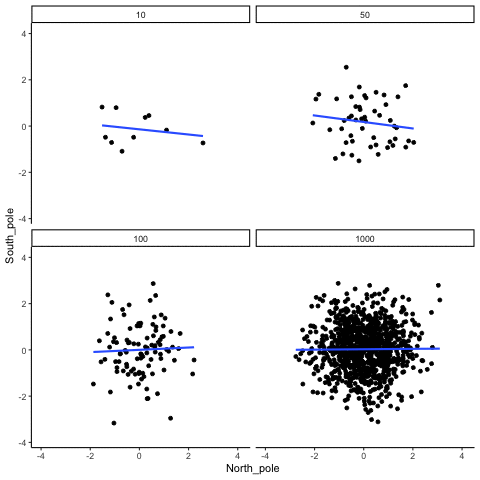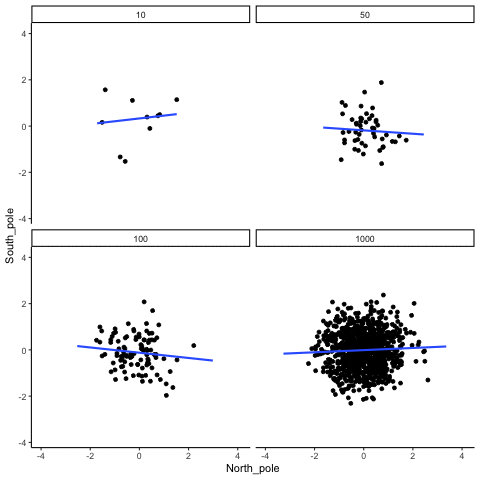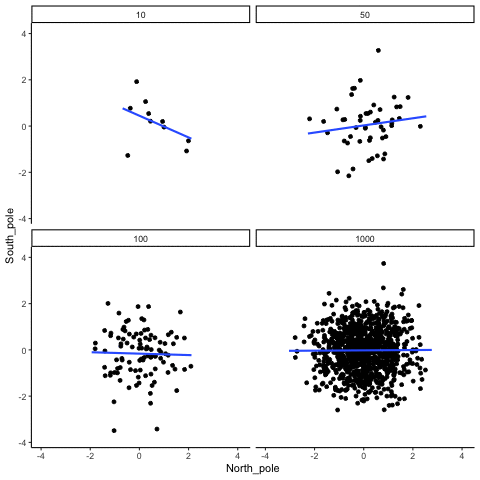
Bien, entonces, ¿cómo se ven las cosas cuando en realidad hay una correlación entre las variables?
Ver cómo se comportan las correlaciones cuando realmente hay una correlación
A veces realmente hay correlaciones entre dos variables que no son causadas por el azar. A continuación, podemos ver una película de cuatro diagramas de dispersión. Cada una muestra la correlación entre dos variables. Nuevamente, cambiamos el tamaño de la muestra en pasos de 10, 50 100 y 1000. Los datos han sido programados para contener una correlación positiva real. Entonces, debemos esperar que la línea vaya subiendo de abajo a la izquierda a la parte superior derecha. Sin embargo, todavía hay variabilidad en los datos. Por lo que esta vez, el error de muestreo debido al azar espolvará la correlación. Sabemos que está ahí, pero a veces el azar hará que se elimine la correlación.
Observe que en el panel superior izquierdo (muestra-tamaño 10), la línea gira mucho más que los otros paneles. Cada nuevo conjunto de muestras produce diferentes correlaciones. En ocasiones, la línea incluso va plana o hacia abajo. No obstante, a medida que aumentamos el tamaño de la muestra, podemos ver que la línea no cambia mucho, siempre va subiendo mostrando una correlación positiva.
La principal conclusión aquí es que incluso cuando hay una correlación positiva entre dos cosas, es posible que no puedas verla si el tamaño de tu muestra es pequeño. Por ejemplo, podrías tener mala suerte con la única muestra que midiste. Tu muestra podría mostrar una correlación negativa, ¡incluso cuando la correlación real es positiva! Desafortunadamente, en el mundo real normalmente solo tenemos la muestra que recolectamos, así que siempre tenemos que preguntarnos si tuvimos suerte o mala suerte. Afortunadamente, si quieres quitar suerte, todo lo que necesitas hacer es recolectar muestras más grandes. Entonces será mucho más probable que observes el patrón real, más bien el patrón que se puede introducir por casualidad.