4.10: Distribuciones de muestreo y teorema del límite central

La ley de los grandes números es una herramienta muy poderosa, pero no va a ser lo suficientemente buena para responder a todas nuestras preguntas. Entre otras cosas, todo lo que nos da es una “garantía a largo plazo”. A la larga, si de alguna manera fuéramos capaces de recopilar una cantidad infinita de datos, entonces la ley de grandes números garantiza que nuestras estadísticas muestrales serán correctas. Pero como John Maynard Keynes argumentó en economía, una garantía a largo plazo es de poca utilidad en la vida real:

[El] a largo plazo es una guía engañosa para la actualidad. A la larga estamos todos muertos. Los economistas se pusieron una tarea demasiado fácil, demasiado inútil, si en temporadas tempestuosas sólo nos pueden decir, que cuando la tormenta ha pasado mucho tiempo, el océano vuelve a estar plano. Keynes (1923, 80)

Como en economía, así también en psicología y estadística. No basta con saber que eventualmente llegaremos a la respuesta correcta al calcular la media muestral. Saber que un conjunto de datos infinitamente grande me dirá el valor exacto de la media de la población es frío confort cuando mi conjunto de datos real tiene un tamaño de muestra de\(N=100\). En la vida real, entonces, debemos saber algo sobre el comportamiento de la media muestral cuando se calcula a partir de un conjunto de datos más modesto!

 

Distribución de muestreo de las medias de la muestra

“Oh no, ¿cuál es la distribución muestral de la muestra media? ¿Eso está permitido incluso en inglés?”. Sí, desafortunadamente, esto está permitido. La distribución muestral de las medias muestrales es lo siguiente más importante que necesitarás entender. ES TAN IMPORTANTE QUE ES NECESARIO USAR TODAS LAS GORRAS. Solo es confuso al principio porque es largo y usa muestreo y muestra en la misma frase.

No te preocupes, te hemos estado preparando para esto. ¿Sabes lo que es una distribución correcta? Es de donde vienen los números. Hace que algunos números ocurran con más o menos frecuencia, o lo mismo que otros números. ¿Sabes lo que es una muestra correcta? Son los números que tomamos de una distribución. Entonces, ¿a qué podría referirse la distribución muestral de las medias muestrales?

Primero, ¿a qué cree que se refiere el medio muestral? Bueno, si tomaras una muestra de números, tendrías un montón de números... entonces, podrías calcular la media de esos números. La media muestral es la media de los números en la muestra. Eso es todo. Entonces, ¿qué es esta distribución de la que hablas? Bueno, y si tomaras un montón de muestras, pones una aquí, pones una ahí, pones algunas otras en otros lugares. Tienes muchas muestras diferentes de números. Se podría calcular la media para cada uno de ellos. Entonces tendrías un montón de medios. ¿Qué aspecto tienen esos medios? Bueno, si los pones en un histograma, podrías averiguarlo. Si lo hicieras, estarías mirando (aproximadamente) una distribución, también conocida como la distribución de muestreo de las medias de la muestra.

“Estoy siguiendo algo así como, ¿por qué querría hacer esto en lugar de ver Netflix...”. Porque, la distribución muestral de los medios de la muestra le da otra ventana al azar. Una muy útil que puedes controlar, al igual que tu mando a distancia, pulsando los botones de diseño correctos.

 

Viendo las piezas

Para realizar una distribución muestral de las medias muestrales, solo necesitamos lo siguiente:

1. Una distribución para tomar números
2. Un montón de muestras diferentes de la distribución
3. Las medias de cada una de las muestras
4. Obtener todas las medias de la muestra y trazarlas en un histograma

Pregunta

Pregunta por ti mismo: ¿Cómo crees que será la distribución muestral de los medios muestrales? ¿Tenderá a verse la forma de la distribución de la que provienen las muestras? ¿O no? Buena pregunta, piénsalo.

Hagamos esas cuatro cosas. Vamos a muestrear números de la distribución uniforme, se ve así si estamos muestreando del conjunto de enteros del 1 al 10:

library(ggplot2)
df<-data.frame(a=1:10,b=seq(.1,1,.1))
df$a<-as.factor(df$a)
ggplot(df,aes(x=a,y=b))+
  geom_point(color="white")+
  geom_hline(yintercept=.1)+
  theme_classic()+
  ylab("Probability")+
  xlab("Number")+
  ggtitle("Uniform distribution for numbers 1 to 10")

Figura\(\PageIndex{1}\): Distribución uniforme que ilustra las probabilidades de muestreo de los números 1 a 10. En una distribución uniforme, todos los números tienen la misma probabilidad de ser muestreados, por lo que la línea es plana indicando que todos los números tienen la misma probabilidad.

Bien, ahora tomemos un montón de muestras de esa distribución. Estableceremos nuestro tamaño de muestra en 20. Es más fácil ver cómo se comporta la media muestra en una película. Cada histograma muestra una nueva muestra. La línea roja muestra dónde está la media de la muestra. Las muestras son todas muy diferentes entre sí, pero la línea roja no se mueve mucho, siempre se queda cerca del medio. Sin embargo, la línea roja sí se mueve un poco, y esta varianza es lo que llamamos la distribución muestral de la media muestral.

Figura\(\PageIndex{2}\): Animiación que muestra histogramas para diferentes muestras de tamaño 20 a partir de la distribución uniforme. La línea roja muestra la media de cada muestra.

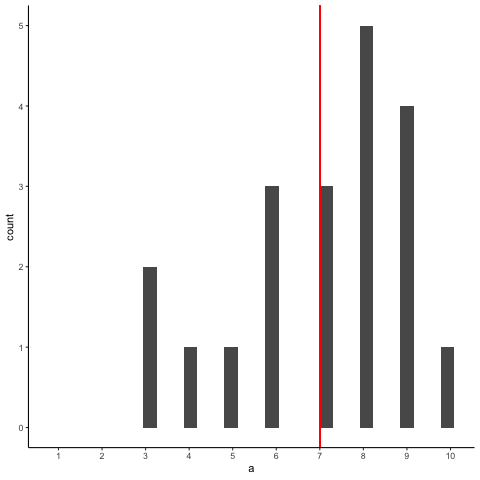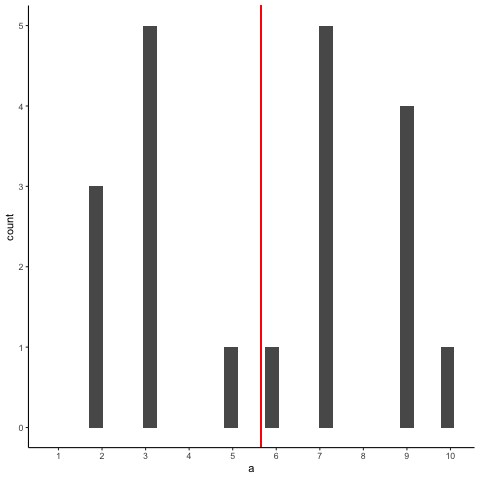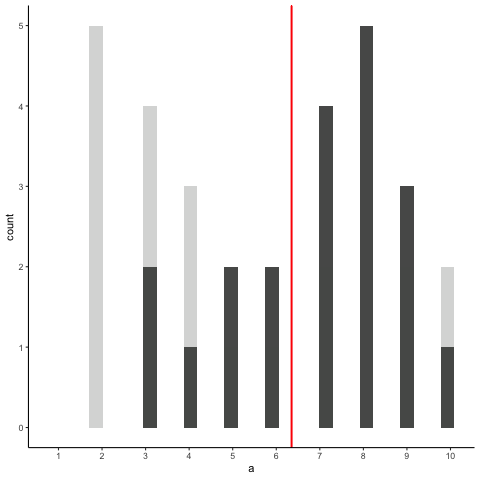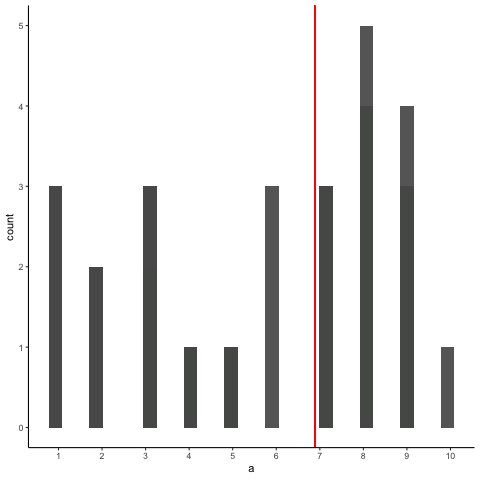
Bien, ¿qué tenemos aquí? Tenemos una animiación de 10 muestras diferentes. Cada muestra tiene 20 observaciones y estas se resumen en cada uno de los histogramas que aparecen en la animiación. Cada histograma tiene una línea roja. La línea roja te muestra dónde se encuentra la media de cada muestra. Entonces, hemos encontrado las medias muestrales para las 10 muestras diferentes de una distribución uniforme.

Primera pregunta. ¿Las medias de la muestra son todas iguales? La respuesta es no. Sin embargo, todos son similares entre sí, son todos alrededor de cinco más o menos algunos números. Esto es interesante. Aunque todas nuestras muestras se ven bastante diferentes entre sí, los medios de nuestras muestras se ven más similares que diferentes.

Segunda pregunta. ¿Qué debemos hacer con los medios de nuestras muestras? Bueno, ¿qué tal si los recogemos todos, y luego trazamos un histograma de ellos? Esto nos permitiría ver cómo es la distribución de la muestra significa. El siguiente histograma es justo esto. Excepto, en lugar de tomar 10 muestras, tomaremos 10,000 muestras. Para cada uno de ellos calcularemos los medios. Entonces, tendremos 10 mil medios. Este es el histograma de las medias de la muestra:

library(ggplot2)
a<-round(runif(20*10000,1,10))
df<-data.frame(a,sample=rep(1:10000,each=20))
df2<-aggregate(a~sample,df,mean)
ggplot(df2, aes(x=a))+
  geom_histogram(color="white", bins=30)+
  theme_classic()+
  ggtitle("Histogram of 10,000 sample means")+
  xlab("value")

Figura\(\PageIndex{3}\): Histograma que muestra las medias muestrales para 10,000 muestras, cada tamaño 20, a partir de la distribución uniforme de números de 1 a 10. La media esperada es 5.5, y el histograma se centra en 5.5. La media de cada muestra no siempre es 5.5 por error de muestreo o probabilidad.

“¿Esperar qué? Esto no se ve bien. Pensé que estábamos tomando muestras de una distribución uniforme. Las distribuciones uniformes son planas. ESTO NO PARECE UN DISTRIBTUION PLANO, LO QUE ESTÁ PASANDO, AAAAAGGGHH”. Sentimos tu dolor.

Recuerde, estamos viendo la distribución de las medias muestrales. En efecto, es cierto que la distribución de las medias muestrales no se ve igual que la distribución de la que tomamos las muestras. Nuestra distribución de medias muestrales va hacia arriba y hacia abajo. De hecho, este será casi siempre el caso de las distribuciones de medias muestrales. A este hecho se le llama el teorema del límite central, del que hablamos más adelante.

Por ahora, hablemos de lo que está pasando. Recuerde, hemos estado muestreando números entre el rango 1 a 10. Se supone que debemos obtener cada número con una frecuencia aproximadamente igual, porque estamos muestreando a partir de una distribución uniforme. Entonces, digamos que tomamos una muestra de 10 números, y por casualidad conseguimos uno de cada uno del 1 al 10.

1 2 3 4 5 6 7 8 9 10

¿Cuál es la media de esos números? Bueno, es 1+2+3+4+5+6+7+8+9+10 = 55/10 = 5.5. Imagínese si tomamos una muestra más grande, digamos de 20 números, y nuevamente obtuvimos exactamente 2 de cada número. ¿Cuál sería la media? Sería (1+2+3+4+5+6+7+8+9+10) *2 = 110/20 = 5.5. Aún 5.5. Puedes ver aquí, que el valor medio de nuestra distribución uniforme es 5.5. Ahora que sabemos esto, podríamos esperar que la mayoría de nuestras muestras tengan una media cercana a este número. Ya sabemos que cada muestra no será perfecta, y no tendrá exactamente la misma cantidad de cada número. Entonces, esperaremos que la media de nuestras muestras varíe un poco. El histograma que hicimos muestra la variación. No es sorprendente que los números varíen alrededor del valor 5.5.

 

¡Existen distribuciones de muestreo para cualquier estadística de muestra!

Una cosa a tener en cuenta a la hora de pensar en distribuciones de muestreo es que cualquier estadística de muestra que le interese calcular tiene una distribución de muestreo. Por ejemplo, supongamos que cada vez que muestreaste algunos números de un experimento escribiste el mayor número en el experimento. Hacer esto una y otra vez le daría una distribución muestreada muy diferente, es decir, la distribución muestral del máximo. Podrías calcular el número más pequeño, o el modo, o la mediana, de la varianza, o la desviación estándar, o cualquier otra cosa de tu muestra. Entonces, podrías repetir muchas veces, y producir la distribución muestral de esas estadísticas. ¡Ordenado!

Solo por diversión aquí hay algunas distribuciones de muestreo diferentes para diferentes estadísticas. Tomaremos una distribución normal con media = 100, y desviación estándar =20. Luego, tomaremos muchas muestras con n = 50 (50 observaciones por muestra). Guardaremos todas las estadísticas de la muestra, luego trazaremos sus histogramas. Hagámoslo:

Figura\(\PageIndex{4}\): Cada panel muestra un histograma de un estadístico de muestreo diferente.

Acabamos de calcular 4 distribuciones de muestreo diferentes, para la media, la desviación estándar, el valor máximo y la mediana. Si solo miras rápidamente estos histogramas podrías pensar que todos básicamente se ven iguales. Aguanta ya. Es muy importante mirar los ejes x. Son diferentes. Por ejemplo, la media muestral va de aproximadamente 90 a 110, mientras que la desviación estándar va de 15 a 25.

Estas distribuciones de muestreo son súper importantes, y vale la pena pensarlas. ¿En qué deberías pensar? Bueno, aquí hay una pista. Estas distribuciones te están diciendo qué esperar de tu muestra. Críticamente, te están diciendo lo que debes esperar de una muestra, cuando tomas una de la distribución específica que usamos (distribución normal con media =100 y DE = 20). Qué hemos aprendido. Hemos aprendido una tonelada. Hemos aprendido que podemos esperar que nuestra muestra tenga una media en algún lugar entre 90 y 108ish. Observe, las medias de la muestra nunca son más extremas. Hemos aprendido que nuestra muestra suele tener alguna varianza, y que la desviación estándar estará en algún lugar entre 15 y 25 (nunca mucho más extrema que eso). Podemos ver que en algún momento obtenemos algunos números grandes, digamos entre 120 y 180, pero no mucho más grandes que eso. Y, podemos ver que la mediana es bastante similar a la media. Si alguna vez tomaste una muestra de 50 números, y tus estadísticas descriptivas estaban dentro de estas ventanas, entonces tal vez vinieron de este tipo de distribución normal. Si tus estadísticas de muestra son muy diferentes, entonces tu muestra probablemente no vino de esta distribución. Mediante el uso de la simulación, podemos averiguar cómo se ven las muestras cuando provienen de distribuciones, y podemos usar esta información para hacer inferencias sobre si nuestra muestra proviene de distribuciones particulares.