4.11: El Teorema del Límite Central

Bien, entonces ahora has visto muchas distribuciones de muestreo, y sabes cuál es la distribución muestral de la media. Aquí, nos centraremos en cómo cambia la distribución muestral de la media en función del tamaño de la muestra.

Intuitivamente, ya conoces parte de la respuesta: si solo tienes unas pocas observaciones, es probable que la media de la muestra sea bastante inexacta (ya la has visto rebotar): si replicas un pequeño experimento y vuelves a calcular la media obtendrás una respuesta muy diferente. Es decir, la distribución muestral es bastante amplia. Si replicas un experimento grande y recalculas la muestra, probablemente obtendrás la misma respuesta que obtuviste la última vez, por lo que la distribución del muestreo será muy estrecha.

Démonos una linda película para ver todo en acción. Vamos a muestrear números de una distribución normal. Verá cuatro paneles, cada panel representa un tamaño de muestra diferente (n), incluyendo tamaños de muestra de 10, 50, 100 y 1000. La línea roja muestra la forma de la distribución normal. Las barras grises muestran un histograma de cada una de las muestras que tomamos. La línea roja muestra la media de una muestra individual (la mitad de las barras grises). Como puede ver, la línea roja se mueve mucho alrededor, sobre todo cuando el tamaño de la muestra es pequeño (10).

Los nuevos bits son las barras azules y las líneas azules. Las barras azules representan la distribución muestral de la media muestral. Por ejemplo, en el panel para muestra-tamaño 10, vemos un montón de barras azules. Se trata de un histograma de 10 medias muestrales, tomadas de 10 muestras de tamaño 10. En el panel de 50, vemos un histograma de 50 medias de muestra, tomadas de 50 muestras de tamaño 50, y así sucesivamente. La línea azul en cada panel es la media de las medias de la muestra (“aaagh, es una media de medias”, sí lo es).

Figura\(\PageIndex{1}\): Animación de muestras (histograma gris muestra recuentos de frecuencia de datos en cada muestra), y la distribución muestral de la media (histograma de las medias de muestreo para muchas muestras). Cada muestra se toma de la distribución normal mostrada en rojo. La línea roja móvil es la media de una muestra individual. La línea azul es la media del histograma azul, que representa la distribución muestral de la media para muchas muestras.

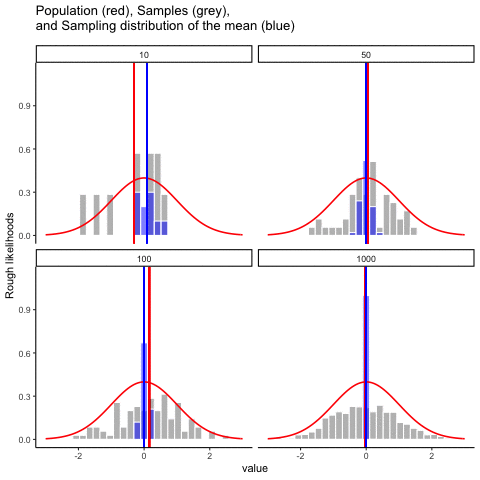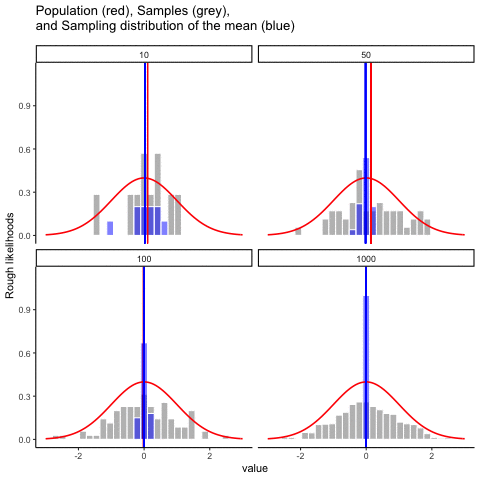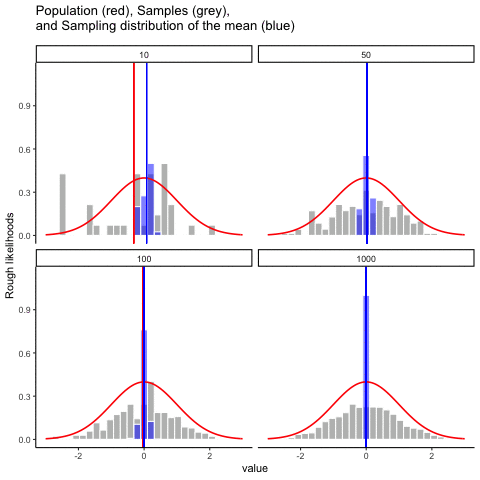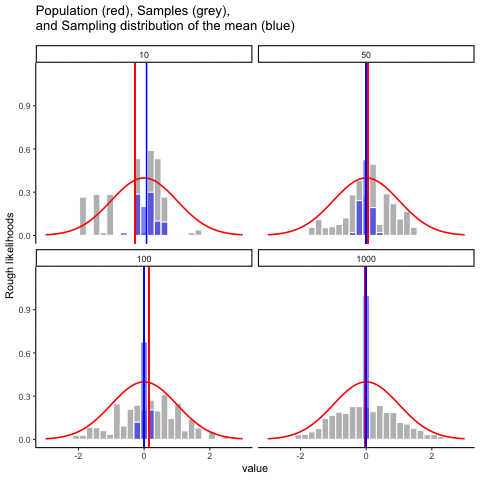
¿Qué deberías notar? Observe que el rango de las barras azules se encoge a medida que aumenta el tamaño de la muestra. La distribución muestral de la media es bastante amplia cuando el tamaño de la muestra es 10, se estrecha a medida que el tamaño de la muestra aumenta a 50 y 100, y es solo una barra, justo en el medio cuando el tamaño de la muestra va a 1000. Lo que estamos viendo es que la media de la distribución muestral se acerca a la media de la población a medida que aumenta el tamaño de la muestra.

Entonces, la distribución muestral de la media es otra distribución, y tiene cierta varianza. Varía más cuando el tamaño de la muestra es pequeño, y varía menos cuando el tamaño de la muestra es grande. Podemos cuantificar este efecto calculando la desviación estándar de la distribución muestral, la cual se conoce como el error estándar. El error estándar de una estadística a menudo se denota SE, y como generalmente nos interesa el error estándar de la media muestral, a menudo usamos el acrónimo SEM. Como puedes ver con solo mirar la película, a medida que\(N\) aumenta el tamaño de la muestra, el SEM disminuye.

Bien, entonces esa es una parte de la historia. Sin embargo, hay algo que hemos estado pasando por alto un poco. Ya lo hemos visto, pero vale la pena mirarlo una vez más. Aquí está la cosa: no importa qué forma sea su distribución poblacional, a medida que\(N\) aumenta la distribución muestral de la media empieza a parecerse más a una distribución normal. Este es el teorema del límite central.

Para ver el teorema del límite central en acción, vamos a ver algunos histogramas de medias de muestra diferentes tipos de distribuciones. ¡Es muy importante reconocer que estás viendo distribuciones de medias de muestra, no distribuciones de muestras individuales! Aquí vamos, comenzando con el muestreo de una distribución normal. La línea roja es la distribución, las barras azules son el histograma para las medias de la muestra. ¡Ambos se ven normales!

library(ggplot2)
options(warn=-1)
get_sampling_means<-function(m,sd,s_size,iter){
  save_means<-length(iter)
  for(i in 1:iter){
    save_means[i]<-mean(rnorm(s_size,m,sd))
  }
  return(save_means)
}
all_df<-data.frame()
sims<-1
n<-50
for(n in c(10,50)){
    sample<-rnorm(n,0,1)
    sample_means<-get_sampling_means(0,1,n,1000)
    t_df<-data.frame(sims=rep(sims,1000),
                     sample,
                     sample_means,
                     sample_size=rep(n,1000),
                     sample_mean=rep(mean(sample),1000),
                     sampling_mean=rep(mean(sample_means),1000)
                     )
    all_df<-rbind(all_df,t_df)
}
ggplot(all_df, aes(x=sample))+
  geom_histogram(aes(x=sample_means,y=(..density..)/max(..density..)),fill="blue",color="white",alpha=.5,bins=75)+
  stat_function(fun = dnorm, 
                args = list(mean = 0, sd = 1), 
                lwd = .75, 
                col = 'red')+
  #geom_vline(aes(xintercept=sampling_mean,frame=sims),color="blue")+
  facet_wrap(~sample_size)+xlim(-3,3)+
  theme_classic()+ggtitle("Sampling distribution of mean \n for Normal Distribution")+ylab("Rough likelihoods")+
  xlab("value")

Figura\(\PageIndex{2}\): Comparación de dos distribuciones normales e histogramas para la distribución muestral de la media para diferentes muestras-tamaños. El rango de distribución muestral de la media se reduce a medida que aumenta el tamaño de la muestra.

Hagámoslo otra vez. En esta ocasión se toma una muestra de una distribución uniforme plana. Nuevamente, vemos que la distribución de las medias muestrales no es plana, parece una distribución normal.

library(ggplot2)
options(warn=-1)
get_sampling_means<-function(mn,mx,s_size,iter){
  save_means<-length(iter)
  for(i in 1:iter){
    save_means[i]<-mean(runif(s_size,mn,mx))
  }
  return(save_means)
}
all_df<-data.frame()
sims<-1
n<-50
for(n in c(10,50)){
    sample<-rnorm(n,0,1)
    sample_means<-get_sampling_means(0,1,n,1000)
    t_df<-data.frame(sims=rep(sims,1000),
                     sample,
                     sample_means,
                     sample_size=rep(n,1000),
                     sample_mean=rep(mean(sample),1000),
                     sampling_mean=rep(mean(sample_means),1000)
                     )
    all_df<-rbind(all_df,t_df)
}
ggplot(all_df, aes(x=sample))+
  geom_histogram(aes(x=sample_means,y=(..density..)/max(..density..)),fill="blue",color="white",alpha=.5,bins=75)+
  geom_hline(yintercept=.1,color="red")+
  facet_wrap(~sample_size)+xlim(0,1)+
  theme_classic()+ggtitle("Sampling distribution of mean \n for samples taken from Uniform Distribution")+ylab("Rough likelihoods")+
  xlab("value")

Figura\(\PageIndex{3}\): Ilustración de que la forma de la distribución muestral de la media es normal, incluso cuando las muestras provienen de una distribución no normal (uniforme en este caso).

Una vez más con una distribución exponencial. Aunque mucho más de los números deberían ser más pequeños que mayores, entonces la distribución de muestreo de la media nuevamente no parece la línea roja. En cambio, se ve más normal-ish. Ese es el teorema del límite central. Simplemente funciona así.

library(ggplot2)
options(warn=-1)
get_sampling_means<-function(s_size,r,iter){
  save_means<-length(iter)
  for(i in 1:iter){
    save_means[i]<-mean(rexp(s_size,r))
  }
  return(save_means)
}
all_df<-data.frame()
sims<-1
n<-50
for(n in c(10,50)){
    sample<-rnorm(n,0,1)
    sample_means<-get_sampling_means(n,2,1000)
    t_df<-data.frame(sims=rep(sims,1000),
                     sample,
                     sample_means,
                     sample_size=rep(n,1000),
                     sample_mean=rep(mean(sample),1000),
                     sampling_mean=rep(mean(sample_means),1000)
                     )
    all_df<-rbind(all_df,t_df)
}
ggplot(all_df, aes(x=sample))+
  geom_histogram(aes(x=sample_means,y=(..density..)/max(..density..)),fill="blue",color="white",alpha=.5,bins=75)+
  stat_function(fun = dexp, 
                args = list(rate=2), 
                lwd = .75, 
                col = 'red')+
  #geom_vline(aes(xintercept=sampling_mean,frame=sims),color="blue")+
  facet_wrap(~sample_size)+xlim(0,1)+
  theme_classic()+ggtitle("Sampling distribution of mean \n for samples from exponential Distribution")+ylab("Rough likelihoods")+
  xlab("value")

Figura\(\PageIndex{4}\): Ilustración de que la forma de la distribución muestral de la media es normal, incluso cuando las muestras provienen de una distribución no normal (exponencial en este caso).

A partir de estas cifras, parece que tenemos evidencia de todas las siguientes afirmaciones sobre la distribución muestral de la media:

• La media de la distribución muestral es la misma que la media de la población
• La desviación estándar de la distribución del muestreo (es decir, el error estándar) se hace más pequeña a medida que aumenta el tamaño de la muestra
• La forma de la distribución del muestreo se vuelve normal a medida que aumenta el tamaño de la muestra

Como sucede, no sólo todas estas afirmaciones son ciertas, hay un teorema muy famoso en la estadística que prueba las tres, conocido como el teorema del límite central. Entre otras cosas, el teorema del límite central nos dice que si la distribución poblacional tiene media\(\mu\) y desviación estándar\(\sigma\), entonces la distribución muestral de la media también tiene media\(\mu\), y el error estándar de la media es

\[\mbox{SEM} = \frac{\sigma}{ \sqrt{N} } \nonumber \]

Debido a que dividimos la desviación estándar de la población\(\sigma\) por la raíz cuadrada del tamaño de la muestra\(N\), el SEM se reduce a medida que aumenta el tamaño de la muestra. También nos dice que la forma de la distribución muestral se vuelve normal.

Este resultado es útil para todo tipo de cosas. Nos dice por qué los experimentos grandes son más confiables que los pequeños, y debido a que nos da una fórmula explícita para el error estándar nos dice cuánto más confiable es un experimento grande. Nos dice por qué la distribución normal es, bueno, normal. En experimentos reales, muchas de las cosas que queremos medir son en realidad promedios de muchas cantidades diferentes (por ejemplo, posiblemente, la inteligencia “general” medida por el coeficiente intelectual es un promedio de un gran número de habilidades y habilidades “específicas”), y cuando eso sucede, la cantidad promedio debe seguir una normalidad distribución. Debido a esta ley matemática, la distribución normal aparece una y otra vez en datos reales.