5.5: La Prueba de Crump
- Page ID
- 150317
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Vamos a estar haciendo mucha inferencia a lo largo del resto de este curso. Bastante todo se reduce a una pregunta. ¿El azar produjo las diferencias en mis datos? Estaremos hablando de experimentos principalmente, y en experimentos queremos saber si nuestra manipulación causó una diferencia en nuestra medición. Pero, medimos cosas que tienen variabilidad natural, así que cada vez que medimos las cosas siempre encontraremos una diferencia. Queremos saber si la diferencia que encontramos (entre nuestras condiciones experimentales) podría haber sido producida por casualidad. Si el azar es una explicación muy poco probable de nuestra diferencia observada, haremos la inferencia de que el azar no produjo la diferencia, y que algo sobre nuestra manipulación experimental sí produjo la diferencia. Esto es (para este libro de texto).
Nota
La estadística no se trata sólo de determinar si el azar podría haber producido un patrón en los datos observados. Las mismas herramientas de las que estamos hablando aquí pueden generalizarse para preguntar si algún tipo de distribución podría haber producido las diferencias. Esto permite realizar comparaciones entre diferentes modelos de los datos, para ver cuál era el más probable, en lugar de simplemente rechazar los improbables (e.g., azar). Pero, dejaremos esos temas avanzados para otro libro de texto.
Este capítulo trata sobre construir intuiciones para hacer este tipo de inferencias sobre el papel del azar en tus datos. No me queda claro cuáles son las mejores cosas para decir, para construir tus intuiciones sobre cómo hacer inferencia estadística. Entonces, este capítulo intenta cosas diferentes, algunas de ellas estándar, y algunas de ellas maquilladas. Lo que estás a punto de leer, es una forma inventada de hacer inferencia estadística, sin usar la jerga que normalmente usamos para hablar de ello. El objetivo es hacer las cosas sin fórmulas, y sin probabilidades, y simplemente trabajar con algunas ideas usando simulaciones para ver qué pasa. Veremos qué puede hacer el azar, luego hablaremos sobre lo que tiene que pasar en tus datos para que tengas la confianza de que el azar no lo hizo.
Métodos intuitivos
Advertencia, se trata de una prueba estadística no oficial conformada por Matt Crump. Tiene sentido para él (yo), y si resulta que alguien más ya lo inventó, entonces Crump no hizo su tarea, y cambiaremos el nombre de esta prueba por su autor original. El objetivo de esta prueba es mostrar cómo las operaciones simples que ya entiendes pueden ser utilizadas para crear una herramienta de inferencia. Esta prueba no es complicada, usa
- Muestreo de números aleatoriamente de una distribución
- Sumando, restando
- División, para encontrar la media
- Contando
- Graficar y dibujar líneas
- SIN FÓRMULAS
Parte 1: Intuición basada en la frecuencia sobre la ocurrencia
Pregunta: ¿Cuántas veces tiene que pasar algo, para que suceda mucho? O bien, ¿cuántas veces tiene que pasar algo para que no suceda mucho, o incluso realmente para nada? ¿Lo suficientemente pequeño como para que no te preocupes de que te pase en absoluto?
¿Irías a la calle todos los días si pensaras que te alcanzaría un rayo 1 de cada 10 veces? Yo no lo haría Probablemente te golpearía un rayo más de una vez al mes, estarías muerto bastante rápido. 1 de cada 10 es mucho (para mí, tal vez no para ti, aquí no hay una respuesta correcta).
¿Irías a la calle todos los días si pensaras que te alcanzaría un rayo 1 de cada 100 días? Cielos, esa es una dura. ¿Qué haría yo siquiera? Si salía todos los días, ¡probablemente estaría muerto en un año! A lo mejor saldría 2 o 3 veces al año, estoy arriesgado así, pero probablemente viviría más tiempo. Chuparía masivamente.
¿Irías a la calle todos los días si pensaras que te alcanzaría un rayo 1 de cada 1000 días? Bueno, probablemente estarías muerto en 3-6 años si hicieras eso. ¿Eres jugador? A lo mejor salir una vez al mes, todavía apesta.
¿Irías a la calle todos los días si pensaras que un rayo te sacaría 1 cada 10.000 días? 10,000 es un número mayor, más difícil de pensar. Es aproximadamente una vez cada 27 años. Sí, probablemente saldría 150 días al año, y viviría un poco más si puedo.
¿Irías a la calle todos los días si pensaras que un rayo te sacaría 1 cada 100 mil días? 100,000 es un número mayor, más difícil de pensar. ¿Cuántos años es eso? Se trata de 273 años. Con esas probabilidades, probablemente saldría todo el tiempo y me olvidaría de ser alcanzado por un rayo. No sucede muy a menudo, y si lo hace, c'est la vie.
El punto de considerar estas preguntas es tener una idea por ti mismo de lo que pasa mucho, y lo que no pasa mucho, y cómo tomarías decisiones importantes en base a lo que pasa mucho y lo que no.
Parte 2: Simulando el azar
Esta siguiente parte podría pasar de muchas maneras, voy a hacer un montón de suposiciones que no voy a defender, y no voy a decir que la prueba Crump tiene problemas. Voy a decir que nos ayuda a hacer una inferencia sobre si el azar podría haber producido algunas diferencias en los datos. Ya nos han introducido a la simulación de cosas, así que volveremos a hacerlo. Esto es lo que vamos a hacer. Soy un psicólogo cognitivo que pasa a estar midiendo X. Debido a investigaciones previas en el campo, sé que cuando mido X, mis muestras tenderán a tener una media y desviación estándar particulares. Digamos que la media suele ser de 100, y la desviación estándar suele ser de 15. En este caso, no me importa usar estos números como estimaciones de los parámetros poblacionales, solo estoy pensando en cómo suelen ser mis muestras. Lo que quiero saber es cómo se comportan cuando los muestro. Quiero ver qué tipo de muestras pasan mucho, y qué tipo de muestras no pasan mucho. Ahora, también vivo en el mundo real, y en el mundo real cuando realizo experimentos para ver qué cambia X, por lo general solo tengo acceso a algún número de participantes, a quienes también estoy muy agradecido, porque ellos participan en mis experimentos. Digamos que normalmente puedo ejecutar 20 sujetos en cada condición en mis experimentos. Mantengamos el experimento simple, con dos condiciones, así que voy a necesitar 40 sujetos en total.
Me gustaría aprender algo que me ayude con la inferencia. Una cosa que me gustaría aprender es cómo se ve la distribución muestral de la media muestral. Esta distribución me dice qué tipos de valores medios suceden mucho, y qué tipos no ocurren muy a menudo. Pero, en realidad voy a saltarme ese pedacito. Porque lo que realmente me interesa es cómo se ve la distribución muestral de la diferencia entre mi muestra significa. Después de todo, voy a hacer un experimento con 20 personas en una condición, y 20 personas en la otra. Entonces voy a calcular la media para el grupo A, y la media para el grupo B, y voy a mirar a la diferencia. Probablemente encontraré una diferencia, pero mi pregunta es, ¿mi manipulación causó esta diferencia, o es este el tipo de cosas que pasan mucho por casualidad? Si supiera lo que puede hacer el azar, y con qué frecuencia produce diferencias de tamaños particulares, podría mirar la diferencia que observé, luego ver qué puede hacer el azar, ¡y luego puedo tomar una decisión! Si mi diferencia no pasa mucho (llegaremos a cuanto no mucho es en un poco), entonces podría estar dispuesto a creer que mi manipulación causó una diferencia. Si mi diferencia ocurre todo el tiempo solo por casualidad, entonces no me inclinaría a pensar que mi manipulación causó la diferencia, porque podría haber sido casualidad.
Entonces, esto es lo que haremos, incluso antes de ejecutar el experimento. Haremos una simulación. Vamos a muestrear los números para el grupo A y el Grupo B, luego computaremos las medias para el grupo A y el grupo B, luego encontraremos la diferencia en las medias entre el grupo A y el grupo B. Pero, haremos una cosa muy importante. Vamos a fingir que en realidad no hemos hecho una manipulación. Si hacemos esto (no hacemos nada, ninguna manipulación que pueda causar una diferencia), entonces sabemos que solo el error de muestreo podría causar alguna diferencia entre la media del grupo A y el grupo B. Hemos eliminado todas las demás causas, solo queda casualidad. Al hacer esto, podremos ver exactamente qué puede hacer el azar. Más importante aún, veremos los tipos de diferencias que ocurren mucho, y los tipos que no ocurren mucho.
Antes de hacer la simulación, necesitamos responder una pregunta. ¿Cuánto es mucho? Podríamos escoger cualquier número para mucho. Voy a escoger 10 mil. Eso es mucho. Si algo pasa solo 1 veces fuera 10,000, estoy dispuesto a decir que no es mucho.
Bien, ahora tenemos nuestro número, vamos a simular las posibles diferencias de medias entre el grupo A y el grupo B que podrían surgir por casualidad. Esto lo hacemos 10 mil veces. Esto da al azar muchas oportunidades para mostrarnos lo que hace, y lo que no hace.
Esto es lo que hice: muestreé 20 números en el grupo A y 20 en el grupo B. Los números procedían ambos de la misma distribución normal, con media = 100, y desviación estándar = 15. Debido a que las muestras provienen de la misma distribución, esperamos que en promedio sean similares (pero ya sabemos que las muestras difieren entre sí). Después, computo la media para cada muestra, y computo la diferencia entre las medias. Yo guardo el puntaje de diferencia media, y termino con 10,000 de ellos. Después dibujo un histograma. Se ve así:
library(ggplot2)
difference<-length(10000)
for(i in 1:10000){
difference[i]<-mean(rnorm(20,100,15)-rnorm(20,100,15))
}
plot_df<-data.frame(sim=1:10000,difference)
ggplot(plot_df,aes(x=difference))+
geom_histogram(bins=100, color="white")+
theme_classic()+
ggtitle("Histogram of mean differences between two samples (n=10) \n
both drawn from the same normal distribution (u=100, sd=20")+
xlab("mean difference")
Nota
Nota al margen: Por supuesto, podríamos reconocer que el azar podría hacer una diferencia mayor a 15. Simplemente no le dimos la oportunidad. Solo ejecutamos la simulación 10 mil veces. Si lo ejecutamos millones de veces, tal vez una diferencia mayor a 20 ocurriría un par de veces. Si lo corriéramos un billón de veces, tal vez una diferencia mayor a 30 ocurriría un par de veces. Si salimos al infinito, entonces el azar podría producir todo tipo de diferencias mayores de vez en cuando. Pero, ya hemos decidido que 1/10,000 no es mucho. Entonces las cosas que pasan 0/10,000 veces, como diferencias mayores a 15, simplemente no pasan mucho.
Ahora podemos ver qué puede hacer el azar con el tamaño de nuestra diferencia de medias. El eje x muestra el tamaño de la diferencia de medias. Tomamos nuestras muestras de la distribución muestral, por lo que la diferencia entre ellas suele ser 0, y eso es lo que vemos en el histograma.
Pausa por un segundo. ¿Por qué las diferencias de medias deberían ser generalmente cero, no era la media poblacional = 100, no deberían estar alrededor de 100? No. La media del grupo A tenderá a ser alrededor de 100, y la media del grupo B tenderá a ser alrededor de 100. Entonces, el puntaje de diferencia tenderá a ser 100-100 = 0. Es por ello que esperamos una diferencia media de cero cuando se extraen las muestras de la misma población.
Entonces, las diferencias cercanas a cero ocurren más, eso es bueno, eso es lo que esperamos. Las diferencias mayores o menores ocurren cada vez con menos frecuencia. Las diferencias mayores a 15 o -15 nunca ocurren en absoluto. Para nuestros propósitos, parece que el azar solo produce diferencias entre -15 y 15.
Bien, hagamos un par de preguntas sencillas. ¿Cuál fue el mayor número negativo que ocurrió en la simulación? Usaremos R para esto. Todos los diez mil puntajes de diferencia se almacenan en una variable que hice llamada diferencia. Si queremos encontrar el valor mínimo, utilizamos la función min. Aquí está el resultado.
Bien, entonces, ¿cuál fue el mayor número positivo que ocurrió? Usemos la función max para averiguarlo. Encuentra el mayor valor (máximo) en la variable. FYI, acabamos de calcular el rango, los números mínimos y máximos en los datos. Recuerden que lo aprendimos antes. En fin, aquí está el máximo.
Ambos valores extremos solo ocurrieron una vez. Esos valores eran tan raros que ni siquiera los pudimos ver en el histograma, la barra era tan pequeña. Además, estos números negativos y positivos más grandes son más o menos del mismo tamaño si ignoras su signo, lo cual tiene sentido porque la distribución parece más o menos simétrica.
Entonces, ¿qué podemos decir de estos dos números para el mínimo y el máximo? Podemos decir que el min pasa 1 veces de 10,000. Podemos decir que el máximo ocurre 1 veces de cada 10,000. ¿Eso es muchas veces? A mí no. No es mucho.
Entonces, ¿con qué frecuencia ocurre una diferencia de 30 (mucho mayor que el máximo) de 10,000. Realmente no podemos decir, los 30 no ocurrieron en la simulación. Yendo con lo que tenemos, decimos 0 de 10 mil. Eso nunca lo es.
Estamos a punto de pasar a la tercera parte, que implica trazar líneas de decisión y hablar de ellas. La parte realmente importante de la parte 3 es ésta. ¿Qué dirías si hicieras este experimento una vez y encontraras una diferencia media de 30? Yo diría que pasa 0 veces de fuera 10,000 por casualidad. Yo diría que el azar no produjo mi diferencia de 30. Eso es lo que yo diría. Vamos a ampliar esto ahora mismo.
Parte 3: Juicio y toma de decisiones
Recuerden, ni siquiera hemos realizado un experimento. Solo estamos simulando lo que podría pasar si hiciéramos un experimento. Hicimos un histograma. Podemos ver que el azar produce algunas diferencias más que otras, y ese azar nunca produjo diferencias realmente grandes. ¿Qué debemos hacer con esta información?
Lo que vamos a hacer es hablar de juicio y toma de decisiones. ¿Qué tipo de juicio y toma de decisiones? Bueno, cuando finalmente hagas un experimento, obtendrás dos medios para el grupo A y B, y luego necesitarás hacer algunos juicios, y tal vez incluso una decisión, si estás tan inclinado. Deberá juzgar si el azar (error de muestreo) podría haber producido la diferencia que observó. Si juzgas que no lo hizo, podrías tomar la decisión de decirle a la gente que tu manipulación experimental realmente funciona. Si juzgas que podría haber sido casualidad, podrías tomar una decisión diferente. Estas son decisiones importantes para los investigadores. Sus carreras pueden depender de ellas. También, sus decisiones importan para el público. Nadie quiere escuchar noticias falsas de los medios sobre hallazgos científicos.
Entonces, lo que estamos haciendo es prepararnos para hacer esos juicios. Vamos a elaborar un plan, incluso antes de que veamos los datos, de cómo vamos a hacer juicios y decisiones sobre lo que encontremos. Este tipo de planeación es extremadamente importante, porque discutimos en la parte 4, que tu planeación puede ayudarte a diseñar un experimento aún mejor que el que podrías haber tenido la intención de ejecutar. Este tipo de planeación también se puede utilizar para interpretar los resultados de otras personas, como una forma de verificar dos veces si cree que esos resultados son plausibles.
Lo que pasa con el juicio y la toma de decisiones es que las personas razonables no están de acuerdo sobre cómo hacerlo, las personas irracionales realmente no están de acuerdo al respecto, y los estadísticos e investigadores no están de acuerdo sobre cómo hacerlo. Voy a proponer algunas cosas con las que la gente no estará de acuerdo. Está bien, estas cosas aún tienen sentido. Y, las cosas desagradables apuntan a problemas importantes que son muy reales para cualquier prueba de inferencia estadística “real”.
Hablemos de algunos hechos objetivos de nuestra simulación de 10,000 cosas que definitivamente sabemos que son ciertas. Por ejemplo, podemos dibujar algunas líneas en la gráfica, y etiquetar algunas regiones diferentes. Hablaremos de dos tipos de regiones.
- Región de azar. Chance lo hizo. El azar podría haberlo hecho
- Región de no casualidad. Chance no lo hizo. Chance no podría haberlo hecho.
Las regiones están definidas por el valor mínimo y el valor máximo. El azar nunca produjo un número menor o mayor. La región dentro del área de distribución es lo que hizo el azar, y la región fuera del rango en ambos lados es lo que el azar nunca hizo. Se ve así:
library(ggplot2)
difference<-length(10000)
for(i in 1:10000){
difference[i]<-mean(rnorm(20,100,15)-rnorm(20,100,15))
}
plot_df<-data.frame(sim=1:10000,difference)
ggplot(plot_df,aes(x=difference))+
annotate("rect", xmin=min(difference), xmax=max(difference), ymin=0,
ymax=Inf, alpha=0.5, fill="red") +
geom_rect(aes(xmin=-Inf, xmax=min(difference), ymin=0, ymax=Inf), alpha=.5,
fill="lightgreen")+
geom_rect(aes(xmin=max(difference), xmax=Inf, ymin=0, ymax=Inf), alpha=.5,
fill="lightgreen")+
geom_histogram(bins=50, color="white")+
theme_classic()+
geom_vline(xintercept = min(difference))+
geom_vline(xintercept = max(difference))+
ggtitle("Histogram of mean differences between two samples (n=10) \n
both drawn from the same normal distribution (u=100, sd=20)")+
xlim(-30,30)+
geom_label(data = data.frame(x = 0, y = 250, label = "CHANCE"),
aes(x = x, y = y, label = label))+
geom_label(data = data.frame(x = -25, y = 250, label = "NOT \n CHANCE"),
aes(x = x, y = y, label = label))+
geom_label(data = data.frame(x = 25, y = 250, label = "NOT \n CHANCE"),
aes(x = x, y = y, label = label))+
geom_label(data = data.frame(x = min(difference), y = 750,
label = paste0("min \n",round(min(difference)))),
aes(x = x, y = y, label = label))+
geom_label(data = data.frame(x = max(difference), y = 750,
label = paste0("max \n",round(max(difference)))),
aes(x = x, y = y, label = label))+
xlab("mean difference")
Acabamos de dibujar algunas líneas, y sombrear algunas regiones, y hemos hecho un plan que podríamos usar para tomar decisiones. Cómo funcionarían las decisiones. Digamos que ejecutaste el experimento y encontraste una diferencia media entre los grupos A y B de 25. ¿Dónde está 25 en la cifra? Está en la parte verde. ¿Qué dice la parte verde? NO AL AZAR. Qué significa esto. Significa que el azar nunca hizo una diferencia de 25. Eso hizo 0 de 10 mil veces. Si encontramos una diferencia de 25, quizás podríamos concluir con confianza que el azar no causó la diferencia. Si encontrara una diferencia de 25 con este tipo de datos, estaría bastante seguro de que mi manipulación experimental causó la diferencia, porque obviamente el azar nunca lo hace.
¿Qué tal una diferencia de +10? Eso es en la parte roja, donde vive el azar. El azar podría haber hecho una diferencia de +10 porque podemos ver que sí lo hizo. La parte roja es la ventana de lo que el azar hizo en nuestra simulación. Cualquier cosa dentro de la ventana podría haber sido una diferencia causada por el azar. Si encontrara una diferencia de +10, diría, podría haber sido casualidad. No estaría muy seguro de que mi manipulación experimental causó la diferencia.
La inferencia estadística podría ser así de fácil. El número que obtienes de tu experimento podría estar en la ventana de oportunidad (entonces no puedes descartar el azar como causa), o podría estar fuera de la ventana de oportunidad (entonces puedes descartar el azar). Caso cerrado. Vayamos todos a casa.
Zonas grises
Entonces, ¿cuál es el problema? Dependiendo de quién seas, y qué tipo de riesgos estés dispuesto a tomar, puede que no haya ningún problema. Pero, si solo eres un poco arriesgado entonces hay un problema que dificulta juicios claros sobre el papel del azar. Nos gustaría decir que el azar causó o no nuestra diferencia. Pero, en realidad siempre estamos en la posición de admitir que a veces podría haber, o no lo habría hecho la mayoría de las veces. Estas son declaraciones lavadas de deseos, están entre sí o no. Eso está bien. El gris también es un color, vamos a darle un poco de respeto al gris.
“¿De qué áreas grises hablas? , sólo veo rojo o verde, ¿soy gris ciego?”. Veamos dónde podrían estar algunas áreas grises. Yo digo que podría ser, porque la gente no está de acuerdo sobre dónde está el gris. Las personas tienen diferentes niveles de confort con el gris. Aquí está mi opinión sobre algunas zonas grises claras.
library(ggplot2)
difference<-length(10000)
for(i in 1:10000){
difference[i]<-mean(rnorm(20,100,15)-rnorm(20,100,15))
}
plot_df<-data.frame(sim=1:10000,difference)
ggplot(plot_df,aes(x=difference))+
annotate("rect", xmin=min(difference), xmax=max(difference), ymin=0,
ymax=Inf, alpha=0.5, fill="red") +
annotate("rect", xmin=min(difference), xmax=min(difference)+10, ymin=0,
ymax=Inf, alpha=0.7, fill="light grey") +
annotate("rect", xmin=max(difference)-10, xmax=max(difference), ymin=0,
ymax=Inf, alpha=0.7, fill="light grey") +
geom_rect(aes(xmin=-Inf, xmax=min(difference), ymin=0, ymax=Inf), alpha=.5,
fill="lightgreen")+
geom_rect(aes(xmin=max(difference), xmax=Inf, ymin=0, ymax=Inf), alpha=.5,
fill="lightgreen")+
geom_histogram(bins=50, color="white")+
theme_classic()+
geom_vline(xintercept = min(difference))+
geom_vline(xintercept = max(difference))+
geom_vline(xintercept = min(difference)+10)+
geom_vline(xintercept = max(difference)-10)+
ggtitle("Histogram of mean differences between two samples (n=10) \n
both drawn from the same normal distribution (u=100, sd=20)")+
xlim(-30,30)+
geom_label(data = data.frame(x = 0, y = 250, label = "CHANCE"),
aes(x = x, y = y, label = label))+
geom_label(data = data.frame(x = -25, y = 250, label = "NOT \n CHANCE"),
aes(x = x, y = y, label = label))+
geom_label(data = data.frame(x = 25, y = 250, label = "NOT \n CHANCE"),
aes(x = x, y = y, label = label))+
geom_label(data = data.frame(x = min(difference), y = 750,
label = paste0("min \n",round(min(difference)))),
aes(x = x, y = y, label = label))+
geom_label(data = data.frame(x = max(difference), y = 750,
label = paste0("max \n",round(max(difference)))),
aes(x = x, y = y, label = label))+
geom_label(data = data.frame(x = -15, y = 250,
label = "?"),
aes(x = x, y = y, label = label))+
geom_label(data = data.frame(x = 15, y = 250,
label = "?"),
aes(x = x, y = y, label = label))+
xlab("mean difference")
Yo hice dos zonas grises, y son de color gris rojizo, porque todavía estamos en la ventana de oportunidad. Hay signos de interrogación (?) en las zonas grises. ¿Por qué? Los interrogantes reflejan cierta incertidumbre que tenemos sobre esas diferencias particulares. Por ejemplo, si encontraste una diferencia que estaba en una zona gris, digamos que un 15. 15 es menor que el máximo, lo que significa que el azar sí creó diferencias de alrededor de 15. Pero, las diferencias de 15 no ocurren muy a menudo.
¿Qué puedes concluir o decir sobre estos 15 que encontraste? ¿Se puede decir sin lugar a dudas que el azar no produjo la diferencia? Por supuesto que no, ya sabes que esa oportunidad podría haber. Aún así, es una de esas cosas que no pasa mucho. Eso hace del azar una explicación poco probable. En lugar de pensar que el azar lo hizo, podrías estar dispuesto a arriesgarte y decir que tu manipulación experimental causó la diferencia. Estarías haciendo una apuesta que no era casualidad... pero, podría ser una apuesta segura, ya que sabes que las probabilidades están a tu favor.
Podrías estar pensando que tus áreas grises no son las mismas que las que he dibujado. A lo mejor quieres ser más conservador, y hacerlos más pequeños. O, a lo mejor eres más arriesgado, y los haría más grandes. O, tal vez agregarías un poco de área gris entrando un poco al área verde (después de todo, el azar probablemente podría producir algunas diferencias mayores a veces, y para evitar esas, tendrías que hacer que el área gris entre un poco en el área verde).
Otra cosa en la que pensar es tu política de decisión. ¿Qué harás, cuando tu diferencia observada esté en tu zona gris? ¿Siempre tomarás la misma decisión sobre el papel del azar? O, a veces vas a flip-flop dependiendo de cómo te sientas. Quizás, piensas que no debería haber una política estricta, y que deberías aceptar algún nivel de incertidumbre. La diferencia que encontraste podría ser real, o puede que no. Hay incertidumbre, es difícil evitarlo.
Así que vamos a ilustrar un tipo más de estrategia para la toma de decisiones. Acabamos de hablar de una que tenía algunas líneas, y algunas regiones. Esto hace que parezca que podemos descartar, o no descartar el papel del azar. Otra forma de ver las cosas es que todo es de un tono diferente de gris. Se ve así:
library(ggplot2)
difference<-length(10000)
for(i in 1:10000){
difference[i]<-mean(rnorm(20,100,15)-rnorm(20,100,15))
}
plot_df<-data.frame(sim=1:10000,difference)
ggplot(plot_df,aes(x=difference))+
# annotate("rect", xmin=min(difference), xmax=max(difference),
# ymin=0, ymax=Inf, alpha=0.5, fill="red") +
annotate("rect", xmin=min(difference), xmax=min(difference)+10, ymin=0,
ymax=Inf, alpha=0.7, fill="light grey") +
annotate("rect", xmin=max(difference)-10, xmax=max(difference), ymin=0,
ymax=Inf, alpha=0.7, fill="light grey") +
geom_rect(aes(xmin=-Inf, xmax=min(difference), ymin=0, ymax=Inf), alpha=.5,
fill="lightgreen")+
geom_rect(aes(xmin=max(difference), xmax=Inf, ymin=0, ymax=Inf), alpha=.5,
fill="lightgreen")+
geom_histogram(bins=50, color="white", aes(fill=..count..))+
theme_classic()+
geom_vline(xintercept = min(difference))+
geom_vline(xintercept = max(difference))+
geom_vline(xintercept = min(difference)+10)+
geom_vline(xintercept = max(difference)-10)+
ggtitle("Histogram of mean differences between two samples (n=10) \n
both drawn from the same normal distribution (u=100, sd=20)")+
xlim(-30,30)+
geom_label(data = data.frame(x = 0, y = 250, label = "CHANCE"),
aes(x = x, y = y, label = label))+
geom_label(data = data.frame(x = -25, y = 250, label = "NOT \n CHANCE"),
aes(x = x, y = y, label = label))+
geom_label(data = data.frame(x = 25, y = 250, label = "NOT \n CHANCE"),
aes(x = x, y = y, label = label))+
geom_label(data = data.frame(x = min(difference), y = 750,
label = paste0("min \n",round(min(difference)))),
aes(x = x, y = y, label = label))+
geom_label(data = data.frame(x = max(difference), y = 750,
label = paste0("max \n",round(max(difference)))),
aes(x = x, y = y, label = label))+
geom_label(data = data.frame(x = -15, y = 250,
label = "?"),
aes(x = x, y = y, label = label))+
geom_label(data = data.frame(x = 15, y = 250,
label = "?"),
aes(x = x, y = y, label = label))+
xlab("mean difference")
OK, así que lo hice tonos de azul (porque era más fácil en R). Ahora podemos ver dos planes de decisión al mismo tiempo. Observe que a medida que las barras se acortan, también se convierten en un azul más oscuro más fuerte. El color se puede utilizar como guía para tu confianza. Es decir, tu confianza en la creencia de que tu manipulación causó la diferencia más que el azar. Si encontraste una diferencia cerca de un bar realmente oscuro, esos no ocurren a menudo por casualidad, así que podrías estar realmente seguro de que el azar no lo hizo. Si encuentra una diferencia cerca de una barra azul ligeramente más clara, es posible que tenga menos confianza. Eso es todo. Ejecutas tu experimento, obtienes tus datos, entonces tienes cierta confianza de que no fue producido por casualidad. Esta forma de pensar se elabora a grados muy interesantes en el mundo bayesiano de la estadística. No nos metemos demasiado en eso, pero mencionarlo un poco aquí y allá. Vale la pena saber que está ahí fuera.
Tomar malas decisiones
No importa cómo planee tomar decisiones sobre sus datos, siempre será propenso a cometer algunos errores. Se podría llamar real a uno hallazgo, cuando en realidad fue causado por casualidad. Esto se llama error tipo I, o falso positivo. Podrías ignorar un hallazgo, llamándolo casualidad, cuando en realidad no era casualidad (aunque estaba en la ventana). Esto se llama un ** tipo II**, o un falso negativo.
La forma de tomar decisiones puede influir en la frecuencia con la que comete errores con el tiempo. Si eres investigador, harás muchos experimentos y cometerás cierta cantidad de errores con el tiempo. Si haces algo así como el método muy estricto de solo aceptar resultados como reales cuando están en la zona de “no chance”, entonces no cometerás muchos errores tipo I. Bastante todo tu resultado será real. Pero, también cometerás errores tipo II, porque perderás cosas cosas reales que tu criterio de decisión dice se deben al azar. Lo contrario también sostiene. Si estás dispuesto a ser más liberal, y aceptar los resultados en el gris como reales, entonces cometerás más errores tipo I, pero no cometerás tantos errores tipo II. Bajo la estrategia de decisión de utilizar estas regiones de corte para la toma de decisiones existe una compensación necesaria. La vista bayesiana se pone un poco alrededor de esto. Los bayesianos hablan de actualizar sus creencias y confianza a lo largo del tiempo. En esa visión, todo lo que tienes es algún nivel de confianza sobre si algo es real, y al ejecutar más experimentos puedes aumentar o disminuir tu nivel de confianza. Esto, de alguna manera, evita algún compromiso entre los errores tipo I y tipo II.
Independientemente, hay otra manera de evitar errores tipo I y tipo II, y aumentar tu confianza en tus resultados, incluso antes de hacer el experimento. Se llama “saber diseñar un buen experimento”.
Parte 4: Diseño de experimentos
Hemos visto lo que puede hacer el azar. Ahora hacemos un experimento. Manipulamos algo entre los grupos A y B, obtenemos los datos, calculamos las medias del grupo, luego miramos la diferencia. Entonces cruzamos todos nuestros dedos de manos y pies, y esperamos más allá de la esperanza que la diferencia sea lo suficientemente grande como para no ser causada por casualidad. Eso es mucha esperanza.
Aquí está la cosa, no solemos saber qué tan fuerte es nuestra manipulación en primer lugar. Entonces, aunque pueda causar un cambio, no necesariamente sabemos cuánto cambio puede causar. Por eso estamos llevando a cabo el experimento. Muchas manipulaciones en Psicología no son lo suficientemente fuertes como para provocar grandes cambios. Esto es un problema para detectar estas pequeñas fuerzas causales. En nuestro ejemplo falso, podrías manipular fácilmente algo que tiene una pequeña influencia, y nunca empujará la diferencia de medias más allá de decir 5 o 10. En nuestra simulación, necesitamos algo más como un 15 o 17 o un 21, o bueno, un 30 sería genial, el azar nunca hace eso. Digamos que tu manipulación es escuchar música o no escuchar música. La escucha de música podría cambiar algo de X, pero si solo cambia X en +5, nunca podrás decir con confianza que no fue casualidad. Y, no es tan fácil cambiar completamente la música y hacer que la música sea súper fuerte en la condición musical por lo que realmente causa un cambio en X en comparación con la condición de no música.
EXPERIMENTO DISEÑO AL RESCATE! Newsflash, a menudo es posible cambiar la forma en que ejecutas tu experimento para que sea más sensible a efectos más pequeños. ¿Cómo crees que podemos hacer esto? Aquí hay una pista. Es lo que aprendiste sobre la distribución de muestreo de la media de la muestra y el papel del tamaño de la muestra. ¿Qué sucede con la distribución muestral de la media de la muestra cuando N (tamaño de la muestra)? La distribución se hace cada vez más estrecha, y comienza a mirar el número único (la media hipotética de la población hipotética). Eso es genial. Si cambias a pensar en puntajes de diferencia media, como la distribución que creamos en esta prueba, ¿qué crees que pasará con esa distribución a medida que aumentemos N? También se encogerá. A medida que aumentemos N al infinito, se encogerá a 0. Lo que significa que, cuando N es infinito, el azar nunca produce ninguna diferencia en absoluto. Podemos usar esto.
Por ejemplo, podríamos ejecutar nuestro experimento con 20 sujetos en cada grupo. O bien, podríamos decidir invertir más tiempo y ejecutar 40 asignaturas en cada grupo, o 80, o 150. Cuando eres el experimentador, llegas a decidir el diseño. Estas decisiones importan a lo grande. Básicamente, cuantos más temas tengas, más sensible será tu experimento. Con N más grande, podrá detectar de manera confiable diferencias medias más pequeñas y poder concluir con confianza que el azar no produjo esos pequeños efectos.
Echa un vistazo a este siguiente conjunto de histogramas. Todo lo que estamos haciendo es la misma simulación que antes, pero esta vez lo hacemos para diferentes tamaños de muestra: 20, 40, 80, 160. Estamos duplicando nuestro tamaño de muestra en cada simulación solo para ver qué sucede con el ancho de la ventana de oportunidad.
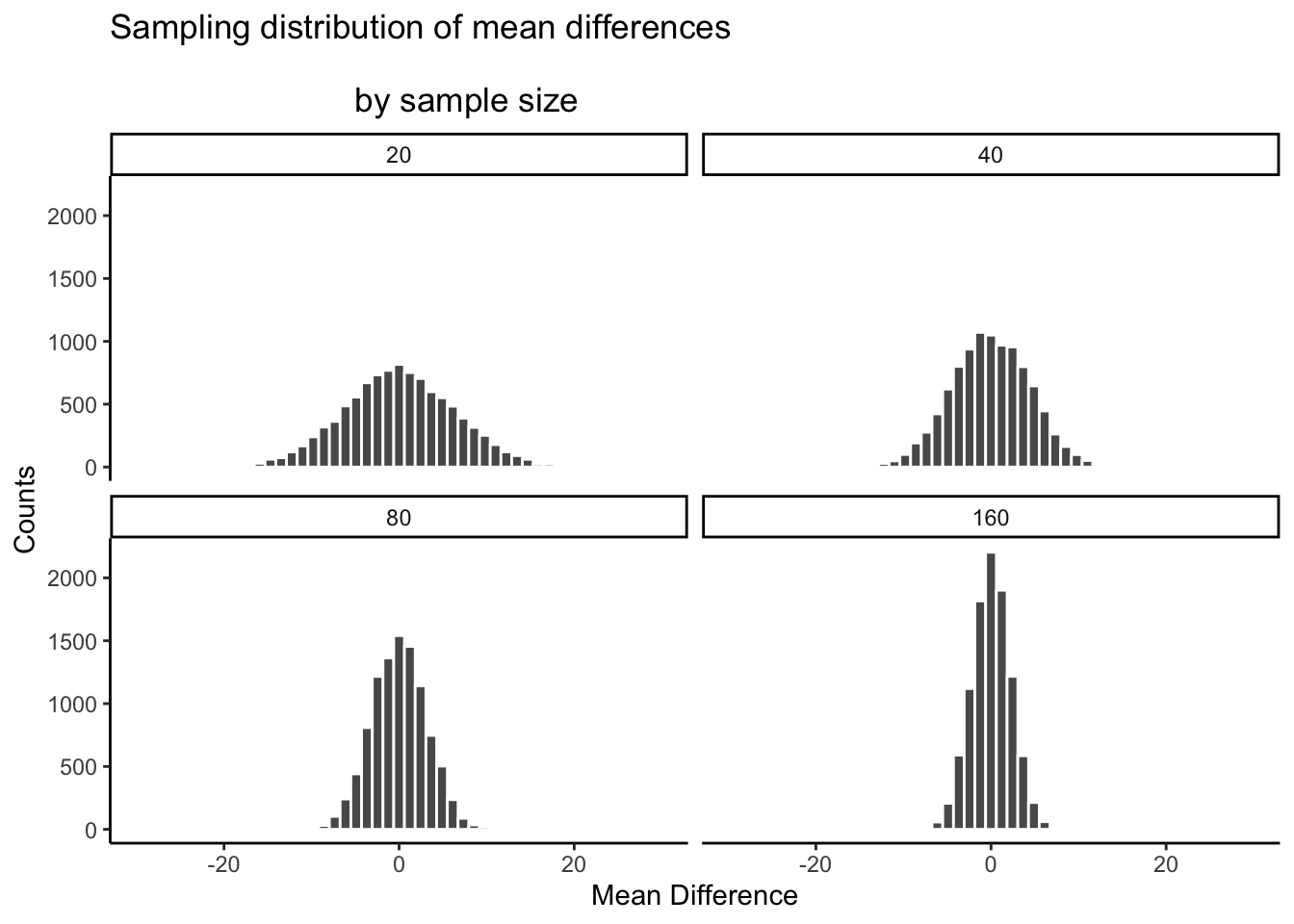
Ahí lo tienes. La distribución muestral de las diferencias medias se reduce hacia 0 a medida que aumenta el tamaño de la muestra. Esto significa que si ejecutas un experimento con un tamaño de muestra más grande, podrás detectar diferencias medias más pequeñas y estar seguro de que no son por casualidad. Veamos una tabla de los valores mínimo y máximo que el azar produjo en estos cuatro tamaños de muestra:
| tamaño_muestra | más pequeño | más grande |
|---|---|---|
| 20 | -25.858660 | 26.266110 |
| 40 | -17.098721 | 16.177815 |
| 80 | -12.000585 | 11.919035 |
| 160 | -9.251625 | 8.357951 |
El cuadro es revelador... El rango de comportamiento del azar es muy amplio para el tamaño de la muestra = 20, pero aproximadamente la mitad de ancho para el tamaño de la muestra = 160.
Si resulta que tu manipulación provocará una diferencia de +11, entonces ¿qué debes hacer? ¿Ejecutar un experimento con 20 personas? Espero que no. Si hiciste eso, podrías obtener +11s con bastante frecuencia por casualidad. Si ejecutaste el experimento con 160 personas, entonces definitivamente podrías decir que +11 no se debió al azar, estaría fuera del rango de lo que puede hacer el azar. Incluso podrías considerar ejecutar el experimento con 80 sujetos. Un +11 allí no sucedería a menudo por casualidad, y sería rentable, gastando menos tiempo en el experimento.
El punto es: el diseño del experimento determina los tamaños de los efectos que puede detectar. Si quieres detectar un pequeño efecto. Haga que su tamaño de muestra sea más grande. Es muy importante decir que esto no es lo único que puedes hacer. También puedes hacer que tus tamaños de celda sean más grandes. Por ejemplo, muchas veces tomamos varias medidas de un solo sujeto. Cuantas más medidas tomes (tamaño de celda), más estable será tu estimación de la media del sujeto. Discutimos estos temas más adelante. También se puede hacer una manipulación más fuerte, cuando sea posible.
Parte 5: Tengo el poder
Por el poder de Greyskull, TENGO EL PODER - He-man
Lo último de lo que hablaremos aquí es algo llamado poder. De hecho, vamos a hablar del concepto de poder, no de poder real. Ahora es confuso, pero después definiremos el poder en términos de algunas ideas particulares sobre la inferencia estadística. Aquí, solo hablaremos de la idea. Y, te mostraremos cómo asegurarte de que tu diseño tenga 100% de potencia. Porque, por qué no. ¿Por qué ejecutar un diseño que no tiene el poder?
La gran idea detrás del poder es el concepto de sensibilidad. El concepto de sensibilidad asume que hay algo a lo que ser sensible. Es decir, hay alguna diferencia real que se puede medir. Entonces, la pregunta es, ¿qué tan sensible es tu experimento? Ya hemos visto que el número de sujetos (tamaño muestral), cambia la sensibilidad del diseño. Más sujetos = más sensibilidad a efectos menores.
Echemos un vistazo a una trama más. Lo que haremos es simular una medida de sensibilidad a través de un montón de tamaños de muestra, de 10 a 300. Esto lo haremos en pasos de 10. Para cada simulación, calcularemos las diferencias de medias como lo hemos hecho. Pero, en lugar de mostrar el histograma, simplemente calcularemos el valor más pequeño y el valor más grande. Esta es una medida bastante buena del alcance exterior del azar. Luego trazaremos esos valores en función del tamaño de la muestra y veremos qué tenemos.
Lo que tenemos aquí es una ventana de sensibilidad razonablemente precisa en función del tamaño de la muestra. Para cada tamaño de muestra, podemos ver la diferencia máxima que produjo el azar y la diferencia mínima. En esas simulaciones, el azar nunca produjo diferencias mayores o menores. Entonces, cada diseño es sensible a cualquier diferencia que esté debajo de la línea de fondo, o por encima de la línea superior. Es realmente así de simple.
Aquí hay otra forma de decirlo. Cuál de los tamaños de muestra será sensible a una diferencia de +10 o -10. Es decir, si se observaba una diferencia de +10 o -10, entonces podríamos decir con mucha confianza que la diferencia no se debió al azar, porque según estas simulaciones, el azar nunca produjo diferencias tan grandes. Para ayudarnos a ver cuáles son sensibles, dibujemos algunas líneas horizontales a -10 y +10.
Yo diría que todos los diseños con tamaño de muestra = 100 o superior son todos perfectamente sensibles a diferencias reales de 10 (si existen). Podemos ver que todos los puntos después del tamaño de muestra 100 están debajo de la línea roja. Entonces, los efectos que son tan grandes como la línea roja, o más grandes casi nunca ocurrirán debido al azar. Pero, si ocurren en la naturaleza, esos experimentos los detectarán de inmediato. Eso es sensibilidad. Y, diseñar tu experimento para que sepas que es sensible a lo que buscas es la gran idea detrás del poder. Vale la pena conocer este tipo de cosas antes de ejecutar tu experimento. Por qué perder su propio tiempo y ejecutar un experimento que no tenga la oportunidad de detectar lo que está buscando.
Resumen de Crump Test
¿Qué aprendimos de esta llamada prueba falsa de Crump que nadie usa? Bueno, aprendimos los fundamentos de lo que vamos a hacer en el futuro. Y, lo hicimos todo sin ninguna matemática o fórmulas duras. Muestreamos números, calculamos medias, restamos medias, luego hicimos eso mucho y contabilizamos las medias y las colocamos en un histograma. Esto nos mostró qué oportunidad hacer en un experimento. Entonces, discutimos cómo tomar decisiones en torno a estos hechos. Y, mostramos cómo podemos manipular el papel del azar simplemente cambiando cosas como el tamaño de la muestra.