5.6: La prueba de aleatorización (prueba de permutación)
- Page ID
- 150325
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Bienvenidos a la primera estadística inferencial oficial de este libro de texto. Hasta ahora hemos estado construyendo algunas intuiciones para ti. A continuación, nos pondremos un poco más formales y te mostraremos cómo podemos usar el azar para decirnos si nuestro hallazgo experimental probablemente se debió al azar o no. Esto lo hacemos con algo llamado prueba de aleatorización. Las ideas detrás de la prueba de aleatorización son las mismas ideas detrás del resto de las estadísticas inferenciales de las que hablaremos en capítulos posteriores. Y, sorpresa, ya hemos hablado de todas las grandes ideas ya. Ahora, solo juntaremos las ideas, y les daremos la prueba de aleatorización de nombres.
Aquí está la gran idea. Cuando ejecutas un experimento y recolectas algunos datos obtienes para averiguar qué pasó esa vez. Pero, debido a que ejecutaste el experimento sólo una vez, no llegas a enterarte de lo que pudo haber pasado. La prueba de aleatorización es una forma de averiguar qué pudo haber sucedido. Y, una vez que lo sepas, puedes comparar lo que sucedió en tu experimento, con lo que pudo haber pasado.
Ejemplo simulado ¿el chicle mejora tus calificaciones?
Digamos que ejecutas un experimento para averiguar si el chicle hace que los estudiantes obtengan mejores calificaciones en los exámenes de estadística. Asigna aleatoriamente a 20 estudiantes a la condición de chicle y a 20 estudiantes diferentes a la condición de no chicle. Entonces, le das a todos pruebas de estadísticas y mides sus calificaciones. Si la goma de mascar causa mejores calificaciones, entonces el grupo de chicles debería tener calificaciones más altas en promedio que el grupo que no masticó chicle.
Digamos que los datos se veían así:
Entonces, ¿les fue mejor a los alumnos que mascaban chicle que a los estudiantes que no masticaban chicle? Observe el rendimiento medio de la prueba en la parte inferior de la tabla. La media para los estudiantes de chicle fue 86.55 y la media para los estudiantes que no masticaron chicle fue de 65.4. Solo mirando los medios, ¡parece que el chicle funcionó!
“PAREN LAS PRENSAS, esto es una tontería”. Ya sabemos que esto es una tontería porque estamos haciendo datos simulados. Pero, aunque se tratara de datos reales, se podría pensar: “Masticar chicle no va a hacer nada, esta diferencia podría haber sido causada por casualidad, quiero decir, tal vez los mejores estudiantes simplemente pasaron a ser puestos en el grupo de masticar, así que por eso sus calificaciones eran más altas, el chicle no hizo nada...”. Estamos de acuerdo. Pero, echemos un vistazo más de cerca. Ya sabemos cómo salen los datos. Lo que queremos saber es cómo podrían haber salido, ¿cuáles son todas las posibilidades?
Por ejemplo, los datos habrían salido un poco diferentes si por casualidad hubiéramos puesto a algunos de los alumnos del grupo chicle en el grupo sin chicle, y viceversa. Piense en todas las formas en que podría haber asignado a los 40 estudiantes en dos grupos, hay muchas formas. Y, los medios para cada grupo resultarían de manera diferente dependiendo de cómo se asignen los alumnos a cada grupo.
Prácticamente hablando, no es posible ejecutar el experimento de todas las formas posibles, eso llevaría demasiado tiempo. Pero, sin embargo, podemos estimar cómo todos esos experimentos podrían haber resultado usando simulación.
Aquí está la idea. Tomaremos las 40 medidas (puntuaciones de examen) que encontramos para todos los alumnos. Entonces tomaremos al azar 20 de ellos y fingiremos que estaban en el grupo de chicles, y tomaremos los 20 restantes y fingiremos que estaban en el grupo sin chicle. Entonces podremos calcular de nuevo los medios para saber qué habría pasado. Podemos seguir haciendo esto una y otra vez. Cada vez que computa lo que sucedió en esa versión del experimento.
Haciendo la aleatorización
Antes de hacer eso, vamos a mostrar cómo funciona la parte de aleatorización. Usaremos menos números para que el proceso sea más fácil de ver. Aquí están los primeros 5 puntajes de exámenes para estudiantes de ambos grupos.
Las cosas podrían haber resultado de manera diferente si algunos de los sujetos del grupo de las encías se cambiaran con los sujetos del grupo sin chicle. Así es como podemos hacer alguna conmutación aleatoria. Haremos esto usando R.
Hemos tomado los primeros 5 números de los datos originales, y los hemos puesto todos en una variable llamada all_scores. Luego usamos la función de muestra en R para barajar las puntuaciones. Finalmente, tomamos los primeros 5 puntajes de los números barajados y los ponemos en una nueva variable llamada new_gum. Después, ponemos los últimos cinco puntajes en la variable new_no_gum. Después los imprimimos, para que los podamos ver.
Si hacemos esto un par de veces y los ponemos en una mesa, efectivamente podemos ver que los medios para chicle y ningún chicle serían diferentes si se barajaran los temas. Compruébalo:
Simulación de las diferencias medias entre las diferentes aleatorizaciones
En nuestro experimento simulado encontramos que la media para los estudiantes de chicle era
, y la media para los estudiantes que no masticaban chicle era
. La diferencia de medias (goma - sin goma) fue
. Esta es una diferencia bastante grande. Esto es lo que sí sucedió. Pero, ¿qué pudo haber pasado? Si probamos todos los experimentos en los que se cambiaron diferentes sujetos, ¿cómo es la distribución de las posibles diferencias de medias? Vamos a averiguarlo. De esto se trata la prueba de aleatorización.
Cuando hagamos nuestra prueba de aleatorización mediremos la diferencia media en las puntuaciones de los exámenes entre el grupo de goma y el grupo sin goma. Cada vez que aleatorizamos guardaremos la diferencia de medias.
Veamos una breve animación de lo que está sucediendo en la prueba de aleatorización. Tenga en cuenta, lo que está a punto de ver son datos de un experimento falso diferente, pero los principios son los mismos. Volveremos al experimento de chicle sin chicle después de la animación. La animación te está mostrando tres cosas importantes. Primero, los puntos morados te muestran las puntuaciones medias en dos grupos (no estudio vs estudio). Parece que hay una diferencia, ya que 1 punto es más bajo que el otro. Queremos saber si el azar podría producir una diferencia tan grande. Al inicio de la animación, los puntos verde claro y rojo muestran las puntuaciones individuales de cada uno de los 10 sujetos del diseño (los puntos morados son la media de estas partituras originales). Ahora, durante las aleatorización, barajamos aleatoriamente las puntuaciones originales entre los grupos. Se puede ver que esto sucede a lo largo de la animación, ya que los puntos verdes y rojos aparecen en diferentes combinaciones aleatorias. Los puntos amarillos en movimiento muestran las nuevas medias para cada grupo después de la aleatorización. Las diferencias entre los puntos amarillos muestran el rango de diferencias que el azar podría producir.
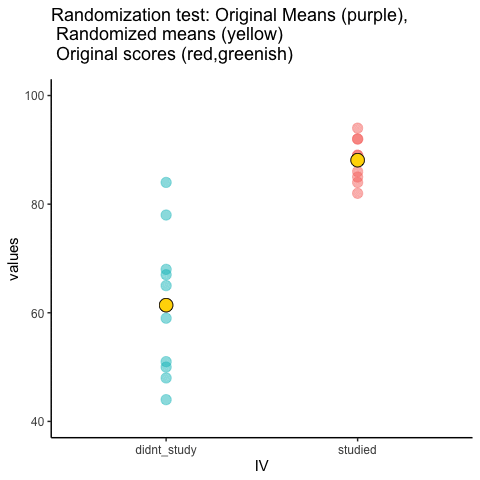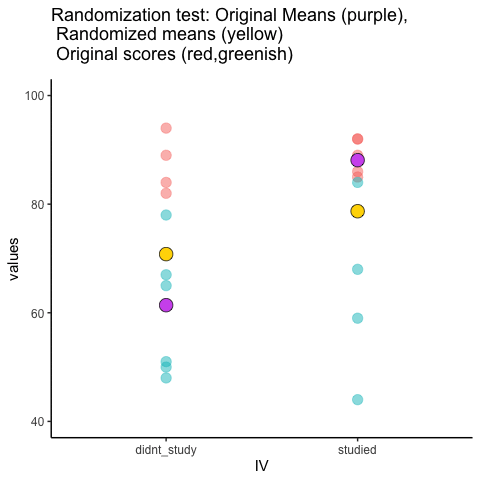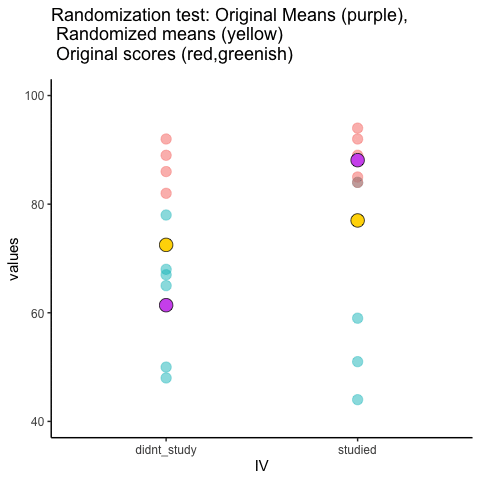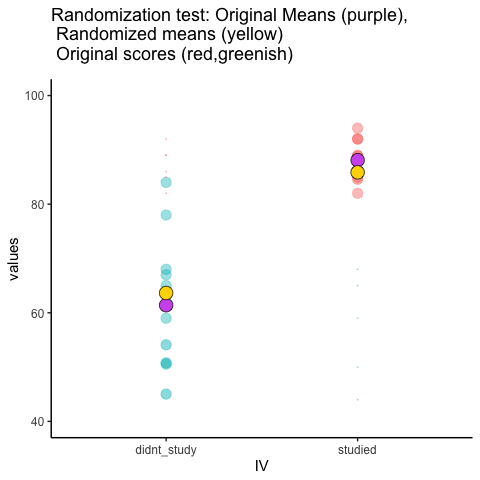
Estamos involucrando en alguna inferencia estadística visual. Al observar el rango de movimiento de los puntos amarillos, estamos viendo qué tipo de diferencias puede producir el azar. En esta animación, los puntos morados, que representan la diferencia original, generalmente están fuera del rango de azar. Los puntos amarillos no se mueven más allá de los puntos morados, como resultado el azar es una explicación poco probable de la diferencia.
Si los puntos morados estuvieran dentro del rango de los puntos amarillos, entonces cuando sabría que el azar es capaz de producir la diferencia que observamos, y que lo hace con bastante frecuencia. En consecuencia, no debemos concluir que la manipulación causó la diferencia, porque fácilmente podría haber ocurrido por casualidad.
Volvamos al ejemplo de chicle. Después de aleatorizar nuestras puntuaciones muchas veces, y computar las nuevas medias, y las diferencias de medias, tendremos muchas diferencias de medias para mirar, que podemos trazar en un histograma. El histograma da una imagen de lo que pudo haber sucedido. Entonces, podemos comparar lo que sucedió con lo que pudo haber pasado.
Aquí está el histograma de las diferencias de medias de la prueba de aleatorización. Para esta simulación, aleatorizamos los resultados del experimento original 1000 veces. Esto es lo que pudo haber pasado. La línea azul en la figura nos muestra dónde se encuentra nuestra diferencia observada en el eje x.
library(ggplot2)
gum<-round(runif(20,70,100))
no_gum<-round(runif(20,40,90))
mean_differences<-length(10000)
for(i in 1:10000){
all<-sample(c(gum,no_gum))
mean_differences[i]<-mean(all[1:20])-mean(all[21:40])
}
rand_df <- data.frame(sims=1:10000,mean_differences)
ggplot(rand_df,aes(x=mean_differences))+
geom_histogram(color="white", bins=30)+
theme_classic()+
geom_vline(color="blue",xintercept=(mean(gum)-mean(no_gum)))
¿Qué opinas? ¿Podría haber sido ocasionada por casualidad la diferencia que representa la línea azul? Mi respuesta probablemente no sea. El histograma nos muestra la ventana del azar. La línea azul no está dentro de la ventana. Esto significa que podemos estar bastante seguros de que la diferencia que observamos no se debió al azar.
Estamos ante otra ventana de oportunidad. Estamos viendo un histograma de los tipos de diferencias de medias que podrían haber ocurrido en nuestro experimento, si hubiéramos asignado a nuestros sujetos a la encía y no grupos de goma de manera diferente. Como puede ver, las diferencias medias van de negativas a positivas. La diferencia más frecuente es 0. Además, la distribución parece ser simétrica alrededor de cero, lo que demuestra que tuvimos aproximadamente las mismas posibilidades de obtener una diferencia positiva o negativa. Además, observe que a medida que las diferencias se hacen mayores (en la dirección positiva o negativa, se vuelven menos frecuentes). La línea azul nos muestra la diferencia observada, esta es la que encontramos en nuestro experimento falso. ¿Dónde está? Es la salida a la derecha. Está bien fuera del histograma. Es decir, cuando miramos lo que pudo haber pasado, vemos que lo que sí sucedió no ocurre muy a menudo.
IMPORTANTE: En este caso, cuando hablamos de lo que pudo haber pasado. Estamos hablando de lo que pudo haber pasado por casualidad. Cuando comparamos lo que sucedió con lo que el azar pudo haber hecho, podemos tener una mejor idea de si nuestro resultado fue causado por el azar.
Bien, pretendamos que tenemos una diferencia de medias mucho menor cuando hicimos el experimento por primera vez. Podemos dibujar nuevas líneas (azul y rojo) para representar una media más pequeña que podríamos haber encontrado.
library(ggplot2)
gum<-round(runif(20,70,100))
no_gum<-round(runif(20,40,90))
mean_differences<-length(10000)
for(i in 1:10000){
all<-sample(c(gum,no_gum))
mean_differences[i]<-mean(all[1:20])-mean(all[21:40])
}
rand_df <- data.frame(sims=1:10000,mean_differences)
ggplot(rand_df,aes(x=mean_differences))+
geom_histogram(color="white",bins=30)+
theme_classic()+
geom_vline(color="blue",xintercept=10)+
geom_vline(color="red",xintercept=5)
Mira la línea azul. Si encontraras una diferencia media de 10, ¿estarías convencido de que tu diferencia no fue causada por casualidad? Como puede ver, la línea azul está dentro de la ventana de oportunidad. Notablemente, las diferencias de +10 no suelen ser muy frecuentes. Podrías inferir que no era probable que tu diferencia se deba al azar (pero podrías ser un poco escéptico, porque podría haber sido). ¿Qué tal la línea roja? La línea roja representa una diferencia de +5. Si encontraras una diferencia de +5 aquí, ¿estarías seguro de que tu diferencia no fue causada por casualidad? Yo no lo estaría. La línea roja está totalmente dentro de la ventana de oportunidad, este tipo de diferencia ocurre con bastante frecuencia. Necesitaría más evidencia para considerar la afirmación de que alguna variable independiente realmente causó la diferencia. Estaría mucho más cómodo asumiendo que el error de muestreo probablemente causó la diferencia.
Lleve sus hogares hasta el momento
¿Te has dado cuenta de que aún no hemos usado ninguna fórmula, pero hemos podido lograr estadísticas inferenciales? Veremos algunas fórmulas a medida que avancemos, pero éstas no son como la idea detrás de las fórmulas.
La estadística inferencial es un intento de resolver el problema: ¿de dónde procedían mis datos? . En el ejemplo de la prueba de aleatorización, nuestra pregunta fue: ¿de dónde provienen las diferencias entre las medias en mis datos? . Sabemos que las diferencias podrían producirse solo por casualidad. Simulamos lo que el azar puede ser debido usando aleatorización. Después trazamos lo que el azar puede hacer usando un histograma. Entonces, solíamos imaginarnos para ayudarnos a hacer una inferencia. ¿Nuestra diferencia observada vino de la distribución, o no? Cuando la diferencia observada está claramente dentro de la distribución de azar, entonces podemos inferir que nuestra diferencia podría haber sido producida por casualidad. Cuando la diferencia observada no está claramente dentro de la distribución de azar, entonces podemos inferir que nuestra diferencia probablemente no se produjo por casualidad.
En mi opinión, estas fotos son muy, muy útiles. Si uno de nuestros objetivos es ayudarnos a resumir un montón de números complicados para llegar a una inferencia, entonces las imágenes hacen un gran trabajo. Ni siquiera necesitamos un número de resumen, solo necesitamos mirar la imagen y ver si la diferencia observada está dentro o fuera de la ventana. De esto se trata todo. Crear formas intuitivas y significativas de hacer inferencias a partir de nuestros datos. A medida que avancemos, lo principal que haremos es formalizar nuestro proceso, y hablar más sobre las estadísticas inferenciales “estándar”. Por ejemplo, en lugar de mirar una imagen (lo cual es algo bueno que hacer), crearemos algunos números útiles. Por ejemplo, ¿y si quisieras la probabilidad de que tu diferencia pudiera haber sido producida por casualidad? Ese podría ser un solo número, como el 95%. Si hubiera un 95% de probabilidad de que el azar pueda producir la diferencia que observaste, es posible que no estés muy seguro de que algo así como tu manipulación experimental estaba causando la diferencia. Si solo hubiera 1% de probabilidad de que el azar pudiera producir tu diferencia, entonces podrías estar más seguro de que el azar no produjo la diferencia; y, en cambio, podrías sentirte cómodo con la posibilidad de que tu manipulación experimental realmente causó la diferencia. Entonces, ¿cómo podemos llegar a esos números? Para llegar allí te presentaremos algunas herramientas más fundamentales para la inferencia estadística.