2.2: Graficar variables cuantitativas
- Page ID
- 150666
Como se discute en la sección sobre variables del Capítulo 1, las variables cuantitativas son variables medidas en una escala numérica. La estatura, el peso, el tiempo de respuesta, la calificación subjetiva del dolor, la temperatura y la puntuación en un examen son ejemplos de variables cuantitativas. Las variables cuantitativas se distinguen de las variables categóricas (a veces llamadas cualitativas) como el color favorito, la religión, la ciudad de nacimiento, el deporte favorito en el que no hay ningún orden o medición involucrados.
Existen muchos tipos de gráficas que se pueden utilizar para retratar distribuciones de variables cuantitativas. Las próximas secciones cubren los siguientes tipos de gráficos:
- exhibidores de tallo y hoja
- histogramas
- polígonos de frecuencia
- parcelas de caja
- gráficos de barras
- gráficas de líneas
- parcelas de puntos
- gráficos de dispersión (discutidos en un capítulo diferente)
Algunos tipos de gráficos, como las pantallas de tallos y hojas, son los más adecuados para cantidades pequeñas a moderadas de datos, mientras que otros, como los histogramas, son los más adecuados para grandes cantidades de datos. Los tipos de gráficos, como las gráficas de caja, son buenos para representar las diferencias entre distribuciones. Las gráficas de dispersión se utilizan para mostrar la relación entre dos variables.
Pantallas de tallo y hoja
Una visualización de tallo y hoja es un método gráfico de visualización de datos. Es particularmente útil cuando sus datos no son demasiado numerosos. En esta sección, explicaremos cómo construir e interpretar este tipo de gráficas.
Como es habitual, comenzaremos con un ejemplo. Considera Figura\(\PageIndex{1}\) que muestra el número de pases de touchdown (pases TD) lanzados por cada uno de los 31 equipos de la Liga Nacional de Futbol en la temporada 2000.

En la Figura se muestra una visualización de tallo y hoja de los datos\(\PageIndex{2}\). La porción izquierda de la Figura\(\PageIndex{2}\) contiene los tallos. Son los números 3, 2, 1 y 0, dispuestos como una columna a la izquierda de las barras. Piense en estos números como dígitos de 10. Un tallo de 3, por ejemplo, se puede utilizar para representar el dígito de los 10 en cualquiera de los números del 30 al 39. Los números a la derecha de la barra son hojas, y representan los dígitos del 1. Por lo tanto, cada hoja en la gráfica representa el resultado de agregar la hoja a 10 veces su tallo.

Para dejar esto claro, examinemos Figura\(\PageIndex{2}\) más de cerca. En la fila superior, las cuatro hojas a la derecha del tallo 3 son 2, 3, 3 y 7. Combinadas con el tallo, estas hojas representan los números 32, 33, 33 y 37, que son los números de pases TD para los cuatro primeros equipos de la Figura\(\PageIndex{1}\). La siguiente fila tiene un tallo de 2 y 12 hojas. En conjunto, representan 12 puntos de datos, es decir, dos ocurrencias de 20 pases TD, tres ocurrencias de 21 pases TD, tres ocurrencias de 22 pases TD, una ocurrencia de 23 pases TD, dos ocurrencias de 28 pases TD y una ocurrencia de 29 pases TD. Te dejamos a ti averiguar qué representa la tercera fila. La cuarta fila tiene un tallo de 0 y dos hojas. Representa las dos últimas entradas en la Figura\(\PageIndex{1}\), a saber, 9 pases TD y 6 pases TD. (Los dos últimos números pueden ser pensados como 09 y 06.)
Un propósito de una exhibición de tallo y hoja es aclarar la forma de la distribución. Se pueden ver muchos datos sobre los pases TD más fácilmente en Figura\(\PageIndex{7}\) que en Figura\(\PageIndex{1}\). Por ejemplo, al mirar los tallos y la forma de la trama, se puede decir que la mayoría de los equipos tuvieron entre 10 y 29 pases de TD, con unos pocos teniendo más y unos pocos teniendo menos. Los números precisos de pases TD se pueden determinar examinando las hojas.
Podemos hacer que nuestra figura sea aún más reveladora dividiendo cada tallo en dos partes. La figura\(\PageIndex{3}\) muestra cómo hacer esto. La fila superior está reservada para números del 35 al 39 y solo contiene los 37 pases TD realizados por el primer equipo en la Figura\(\PageIndex{1}\). La segunda fila está reservada para los números del 30 al 34 y sostiene los pases de 32, 33 y 33 TD realizados por los siguientes tres equipos de la tabla. Puedes ver por ti mismo lo que representan las otras filas.

F igure\(\PageIndex{3}\) es más revelador que Figura\(\PageIndex{2}\) porque esta última figura agrupa demasiados valores en una sola fila. Si debe dividir los tallos en una pantalla depende de la forma exacta de sus datos. Si las filas se alargan demasiado con tallos individuales, podrías intentar dividirlas en dos o más partes.
Existe una variación de las pantallas de tallo y hoja que es útil para comparar distribuciones. Las dos distribuciones se colocan espalda con espalda a lo largo de una columna común de tallos. El resultado es una “exhibición de tallo y hoja consecutiva”. La figura\(\PageIndex{4}\) muestra dicha gráfica. Compara los números de pases TD en las temporadas 1998 y 2000. Los tallos están en el medio, las hojas a la izquierda son para los datos de 1998 y las hojas a la derecha son para los datos de 2000. Por ejemplo, la penúltima fila muestra que en 1998 hubo equipos con 11, 12 y 13 pases TD, y en 2000 hubo dos equipos con 12 y tres equipos con 14 pases TD.
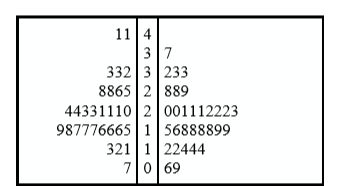
La cifra nos\(\PageIndex{4}\) ayuda a ver que las dos temporadas fueron similares, pero que sólo en 1998 algún equipo lanzó más de 40 pases TD.
Hay dos cosas sobre los datos futbolísticos que hacen que sean fáciles de graficar con tallos y hojas. Primero, los datos se limitan a números enteros que se pueden representar con un tallo de un dígito y una hoja de un dígito. Segundo, todos los números son positivos. Si los datos incluyen números con tres o más dígitos, o contienen decimales, se pueden redondear a una precisión de dos dígitos. Los valores negativos también se manejan fácilmente. Veamos otro ejemplo.
La figura\(\PageIndex{5}\) muestra datos del estudio de caso Armas y agresión. Cada valor es la diferencia media a lo largo de una serie de ensayos entre las veces que tomó a un sujeto experimental nombrar palabras agresivas (como “punch”) bajo dos condiciones. En una condición, las palabras fueron precedidas por una palabra no arma como “bug”. En la segunda condición, las mismas palabras fueron precedidas por una palabra arma como “arma” o “cuchillo”. El tema abordado por el experimento fue si una palabra arma precedente aceleraría (o cebaría) la pronunciación de la palabra agresiva en comparación con una palabra que no es de preparación de armas. Una diferencia positiva implica un mayor cebado de la palabra agresiva por la palabra arma. Las diferencias negativas implican que el cebado por la palabra arma fue menor que para una palabra neutra.

Ves que los números van desde 43.2 hasta -27.4. El primer valor indica que un sujeto fue 43.2 milisegundos más rápido pronunciando palabras agresivas cuando fueron precedidas por palabras de arma que cuando precedieron por palabras neutras. El valor 27.4 indica que otro sujeto fue 27.4 milisegundos más lento pronunciando palabras agresivas cuando fueron precedidas por palabras de arma.
Los datos se muestran con tallos y hojas en la Figura\(\PageIndex{6}\). Dado que las pantallas de tallo y hoja solo pueden retratar dos dígitos enteros (uno para el tallo y otro para la hoja), los números se redondean primero. Así, el valor 43.2 se redondea a 43 y se representa con un tallo de 4 y una hoja de 3. De igual manera, 42.9 se redondea a 43. Para representar números negativos, simplemente usamos tallos negativos. Por ejemplo, la fila inferior de la figura representa el número —27. La penúltima fila representa los números -10, -10, -15, etc. Una vez más, hemos redondeado los valores originales de la Figura\(\PageIndex{5}\).

Observe que la figura contiene una fila encabezada por “0” y otra encabezada por “-0”. El tallo de 0 es para números entre 0 y 9, mientras que el tallo de -0 es para números entre 0 y -9. Por ejemplo, la quinta fila de la tabla contiene los números 1, 2, 4, 5, 5, 8, 9 y la sexta fila contiene 0, -6, -7 y -9. Los valores que son exactamente 0 antes del redondeo deben dividirse lo más uniformemente posible entre las filas “0” y “-0”. En la Figura\(\PageIndex{5}\), ninguno de los valores es 0 antes del redondeo. El “0” que aparece en la fila “-0” proviene del valor original de -0.2 en la tabla.
Aunque las presentaciones de tallos y hojas son difíciles de manejar para grandes conjuntos de datos, a menudo son útiles para conjuntos de datos con hasta 200 observaciones. La\(\PageIndex{7}\) figura muestra la distribución de las poblaciones de 185 ciudades estadounidenses en 1998. Para ser incluida, una ciudad tenía que tener entre 100 mil y 500 mil habitantes.

Dado que una parcela de tallo y hoja muestra solo una precisión de dos lugares, tuvimos que redondear los números a los 10,000 más cercanos. Por ejemplo, el mayor número (493,559) se redondeó a 490,000 y luego se trazó con un tallo de 4 y una hoja de 9. El cuarto número más alto (463,201) se redondeó a 460,000 y se trazó con un tallo de 4 y una hoja de 6. Así, los tallos representan unidades de 100,000 y las hojas representan unidades de 10,000. Observe que cada valor de tallo se divide en cinco partes: 0-1, 2-3, 4-5, 67 y 8-9.
Si sus datos pueden ser adecuadamente representados por una visualización de tallo y hoja depende de si se pueden redondear sin pérdida de información importante. Además, sus valores extremos deben encajar en dos dígitos sucesivos, ya que los datos de la Figura 11 encajan en los lugares 10,000 y 100,000 (para hojas y tallos, respectivamente). Decidir qué tipo de gráfico es el más adecuado para mostrar sus datos, por lo tanto, requiere un buen juicio. ¡La estadística no es solo recetas!
Histogramas
Un histograma es un método gráfico para mostrar la forma de una distribución. Es particularmente útil cuando hay un gran número de observaciones. Comenzamos con un ejemplo consistente en las puntuaciones de 642 estudiantes en una prueba de psicología. La prueba consta de 197 ítems cada uno calificado como “correcto” o “incorrecto”. Los puntajes de los estudiantes oscilaron entre 46 y 167.
El primer paso es crear una tabla de frecuencias. Desafortunadamente, una tabla de frecuencias simple sería demasiado grande, conteniendo más de 100 filas. Para simplificar la tabla, agrupamos las puntuaciones como se muestra en Tabla\(\PageIndex{1}\).
| I nterval Inferior Limi t | Límite superior del intervalo | Frecuencia de clase |
|---|---|---|
| 39.5 | 49.5 | 3 |
| 49.5 | 59.5 | 10 |
| 59.5 | 69.5 | 53 |
| 69.5 | 79.5 | 107 |
| 79.5 | 89.5 | 147 |
| 89.5 | 99.5 | 130 |
| 99.5 | 109.5 | 78 |
| 109.5 | 119.5 | 59 |
| 119.5 | 129.5 | 36 |
| 129.5 | 139.5 | 11 |
| 139.5 | 149.5 | 6 |
| 149.5 | 159.5 | 1 |
| 159.5 | 169.5 | 1 |
Para crear esta tabla, el rango de puntuaciones se dividió en intervalos, llamados intervalos de clase. El primer intervalo es de 39.5 a 49.5, el segundo de 49.5 a 59.5, etc. A continuación, se contó el número de puntuaciones que caen en cada intervalo para obtener las frecuencias de clase. Hay tres puntuaciones en el primer intervalo, 10 en el segundo, etc.
Los intervalos de clase de ancho 10 proporcionan suficientes detalles sobre la distribución para ser reveladores sin hacer que la gráfica sea demasiado “entrecortada”. Más información sobre cómo elegir los anchos de los intervalos de clase se presenta más adelante en esta sección. Colocar los límites de los intervalos de clase a medio camino entre dos números (por ejemplo, 49.5) asegura que cada puntaje caerá en un intervalo en lugar de en el límite entre intervalos.
En un histograma, las frecuencias de clase están representadas por barras. La altura de cada barra corresponde a su frecuencia de clase. Un histograma de estos datos se muestra en la Figura\(\PageIndex{8}\).
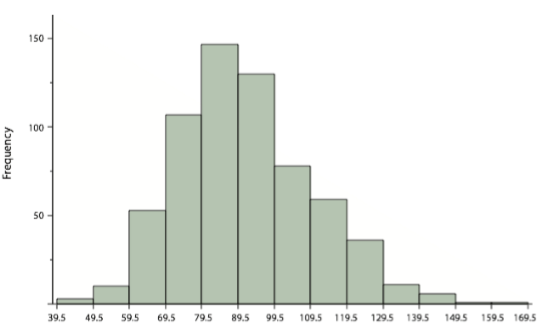
El histograma deja claro que la mayoría de las puntuaciones están en el medio de la distribución, con menos puntuaciones en los extremos. También se puede ver que la distribución no es simétrica: las puntuaciones se extienden hacia la derecha más lejos que a la izquierda. Por lo tanto, se dice que la distribución está sesgada. (Tendremos más que decir sobre las formas de las distribuciones en el Capítulo 3.)
En nuestro ejemplo, las observaciones son números enteros. Los histogramas también se pueden usar cuando las puntuaciones se miden en una escala más continua, como el tiempo (en milisegundos) requerido para realizar una tarea. En este caso, no hay necesidad de preocuparse por los guardadores de bardas ya que son improbables. (Sería toda una coincidencia que una tarea requiriera exactamente 7 segundos, medidos a la milésima de segundo más cercana). Por lo tanto, somos libres de elegir números enteros como límites para nuestros intervalos de clase, por ejemplo, 4000, 5000, etc. La frecuencia de clase es entonces el número de observaciones que son mayores o iguales al límite inferior, y estrictamente menores que el límite superior. Por ejemplo, un intervalo podría contener tiempos de 4000 a 4999 milisegundos. Usar números enteros como límites evita una apariencia desordenada, y es la práctica de muchos programas de computadora que crean histogramas. Tenga en cuenta también que algunos programas de computadora etiquetan la mitad de cada intervalo en lugar de los puntos finales.
Los histogramas pueden basarse en frecuencias relativas en lugar de frecuencias reales. Los histogramas basados en frecuencias relativas muestran la proporción de puntuaciones en cada intervalo en lugar del número de puntuaciones. En este caso, el eje Y va de 0 a 1 (o en algún punto intermedio si no hay proporciones extremas). Puede cambiar un histograma basado en frecuencias a uno basado en frecuencias relativas (a) dividiendo cada frecuencia de clase por el número total de observaciones, y luego (b) trazando los cocientes en el eje Y (etiquetado como proporción).
Hay más que decir sobre los anchos de los intervalos de clase, a veces llamados anchos de bin. Su elección de ancho de contenedor determina el número de intervalos de clase. Esta decisión, junto con la elección del punto de partida para el primer intervalo, afecta la forma del histograma. El mejor consejo es experimentar con diferentes opciones de ancho, y elegir un histograma de acuerdo a lo bien que comunique la forma de la distribución.
Polígonos de frecuencia
Los polígonos de frecuencia son un dispositivo gráfico para comprender las formas de las distribuciones. Sirven para el mismo propósito que los histogramas, pero son especialmente útiles para comparar conjuntos de datos. Los polígonos de frecuencia también son una buena opción para mostrar distribuciones de frecuencia acumulativas.
Para crear un polígono de frecuencia, comience igual que para los histogramas, eligiendo un intervalo de clase. Luego dibuja un eje X que represente los valores de las puntuaciones en tus datos. Marque el medio de cada intervalo de clase con una marca de verificación y etiquételo con el valor medio representado por la clase. Dibuja el eje Y para indicar la frecuencia de cada clase. Colocar un punto en el medio de cada intervalo de clase a la altura correspondiente a su frecuencia. Por último, conectar los puntos. Debe incluir un intervalo de clase por debajo del valor más bajo en sus datos y uno por encima del valor más alto. Luego, la gráfica tocará el eje X en ambos lados.
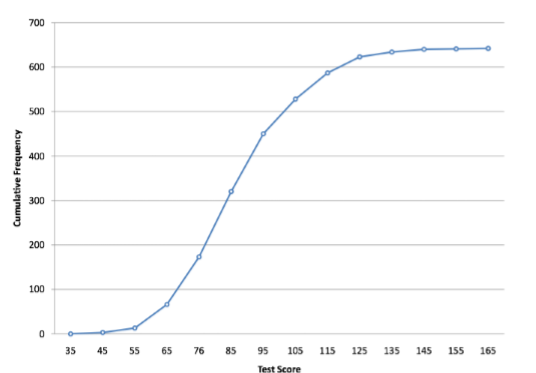
Se construyó un polígono de frecuencia para 642 puntuaciones de pruebas de psicología mostradas en la Figura\(\PageIndex{8}\) a partir de la tabla de frecuencias que se muestra en Tabla\(\PageIndex{2}\).
| Límite Inferior | Límite superior | Contar | Recuento Acumulado |
|---|---|---|---|
| 29.5 | 39.5 | 0 | 0 |
| 39.5 | 49.5 | 3 | 3 |
| 49.5 | 59.5 | 10 | 13 |
| 59.5 | 69.5 | 53 | 66 |
| 69.5 | 79.5 | 107 | 173 |
| 79.5 | 89.5 | 147 | 320 |
| 89.5 | 99.5 | 130 | 450 |
| 99.5 | 109.5 | 78 | 528 |
| 109.5 | 119.5 | 59 | 587 |
| 119.5 | 129.5 | 36 | 623 |
| 129.5 | 139.5 | 11 | 634 |
| 139.5 | 149.5 | 6 | 640 |
| 149.5 | 159.5 | 1 | 641 |
| 159.5 | 169.5 | 1 | 642 |
| 169.5 | 170.5 | 0 | 642 |
La primera etiqueta en el eje X es 35. Esto representa un intervalo que se extiende de 29.5 a 39.5. Dado que el puntaje de prueba más bajo es 46, este intervalo tiene una frecuencia de 0. El punto etiquetado 45 representa el intervalo de 39.5 a 49.5. Hay tres puntajes en este intervalo. Hay 147 puntajes en el intervalo que rodea a 85.
Se puede discernir fácilmente la forma de la distribución de Figura\(\PageIndex{9}\). La mayoría de los puntajes están entre 65 y 115. Es claro que la distribución no es simétrica en la medida en que los buenos puntajes (a la derecha) se alejan más gradualmente que los malos puntajes (a la izquierda). En la terminología del Capítulo 3 (donde estudiaremos formas de distribuciones de manera más sistemática), la distribución es sesgada.
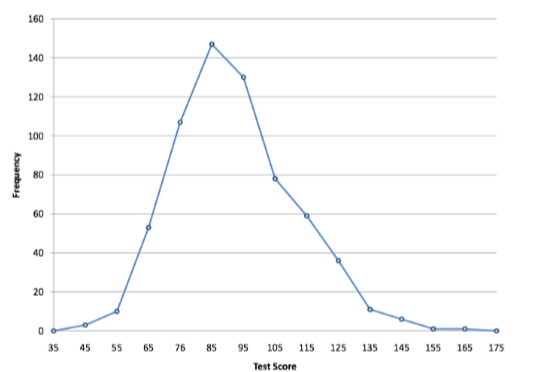
Figura\(\PageIndex{9}\): Polígono de frecuencia para las puntuaciones de las pruebas de psicología.
En la Figura se muestra un polígono de frecuencia acumulativa para las mismas puntuaciones de prueba\(\PageIndex{10}\). La gráfica es la misma que antes excepto que el valor Y para cada punto es el número de alumnos en el intervalo de clase correspondiente más todos los números en intervalos inferiores. Por ejemplo, no hay puntuaciones en el intervalo etiquetado como “35”, tres en el intervalo “45” y 10 en el intervalo “55". Por lo tanto, el valor Y correspondiente a “55” es 13. Dado que 642 estudiantes tomaron la prueba, la frecuencia acumulada para el último intervalo es 642.
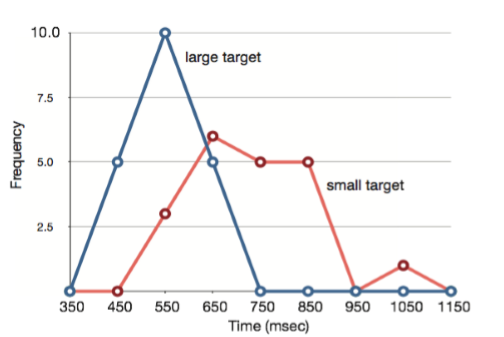
Los polígonos de frecuencia son útiles para comparar distribuciones. Esto se logra superponiendo los polígonos de frecuencia dibujados para diferentes conjuntos de datos. La Figura 2.1.3 proporciona un ejemplo. Los datos provienen de una tarea en la que el objetivo es mover un cursor de computadora a un objetivo en la pantalla lo más rápido posible. En 20 de los ensayos, el objetivo era un rectángulo pequeño; en los otros 20, el objetivo era un rectángulo grande. En cada ensayo se registró el tiempo para alcanzar el objetivo. Las dos distribuciones (una para cada objetivo) se trazan juntas en la Figura\(\PageIndex{11}\). La figura muestra que, aunque hay cierta superposición en los tiempos, generalmente tardó más tiempo en mover el cursor al objetivo pequeño que al grande.
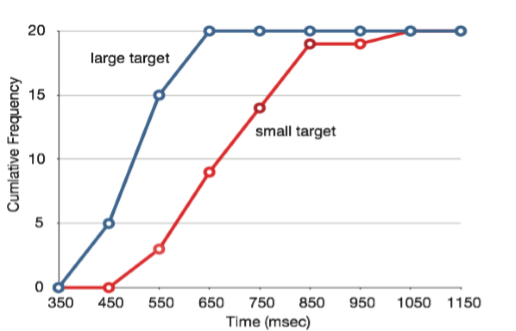
También es posible trazar dos distribuciones de frecuencia acumuladas en una misma gráfica. Esto se ilustra en la Figura\(\PageIndex{12}\) usando los mismos datos de la tarea del cursor. La diferencia en las distribuciones para los dos objetivos vuelve a ser evidente.
Gráficas de caja Ya hemos discutido técnicas para representar visualmente datos (ver histogramas y polígonos de frecuencia). En esta sección presentamos otra gráfica importante, llamada trama de caja. Las gráficas de caja son útiles para identificar valores atípicos y para comparar distribuciones. Explicaremos parcelas de caja con la ayuda de datos de un experimento en clase. A los estudiantes de Estadística Introductoria se les presentó una página que contenía 30 rectángulos coloreados. Su tarea era nombrar los colores lo más rápido posible. Se registraron sus tiempos (en segundos). Compararemos las puntuaciones de los 16 hombres y 31 mujeres que participaron en el experimento haciendo parcelas de caja separadas para cada género. Tal visualización se dice que involucra parcelas de caja paralelas.
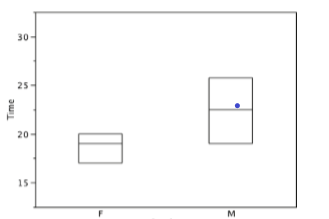
Hay varios pasos en la construcción de una parcela de caja. El primero se basa en los percentiles 25, 50 y 75 en la distribución de las puntuaciones. La figura\(\PageIndex{14}\) muestra cómo se utilizan estas tres estadísticas. Para cada género dibujamos una caja que se extiende desde el percentil 25 hasta el percentil 75. El percentil 50 se dibuja dentro de la caja. Por lo tanto, la parte inferior de cada caja es el percentil 25, la parte superior es el percentil 75, y la línea en el medio es el percentil 50. Los datos de las mujeres de nuestra muestra se muestran en la Figura\(\PageIndex{13}\).

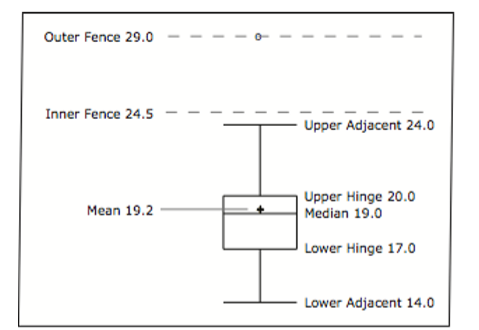
Para estos datos, el percentil 25 es 17, el percentil 50 es 19 y el percentil 75 es 20. Para los hombres (cuyos datos no se muestran), el percentil 25 es 19, el percentil 50 es 22.5 y el percentil 75 es 25.5.
Antes de continuar, la terminología en Table\(\PageIndex{3}\) es útil.
| Nombre | Fórmula | Valor |
|---|---|---|
| Bisagra Superior | Percentil 75 | 20 |
| Bisagra Inferior | Percentil 25 | 17 |
| H-Spread | Bisagra Superior - Bisagra Inferior | 3 |
| Paso | 1.5 x Extendibles en H | 4.5 |
| Cerca Interior Superior | Bisagra Superior + 1 Escalón | 24.5 |
| Cerca Interior Inferior | Bisagra Inferior - 1 Escalón | 12.5 |
| Cerca Exterior Superior | Bisagra Superior + 2 Escalones | 29 |
| Cerca Exterior Inferior | Bisagra Inferior - 2 Escalones | 8 |
| Adyacente superior | Valor más grande debajo de la cerca interior superior | 24 |
| Inferior adyacente | Valor más pequeño por encima de la cerca interior inferior | 14 |
| Valor Exterior | Un valor más allá de una cerca interior pero no más allá de una cerca exterior | 29 |
| Valor lejano | Un valor más allá de una cerca exterior | Ninguno |
Continuando con las parcelas de caja, colocamos “bigotes” arriba y debajo de cada caja para dar información adicional sobre la propagación de los datos. Los bigotes son líneas verticales que terminan en un trazo horizontal. Los bigotes se dibujan desde las bisagras superior e inferior hasta los valores adyacentes superior e inferior (24 y 14 para los datos de las mujeres), como se muestra en la Figura\(\PageIndex{15}\).
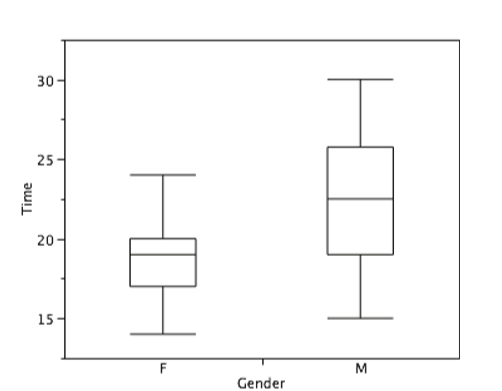
Figura\(\PageIndex{15}\): Las parcelas de caja con los bigotes dibujados.
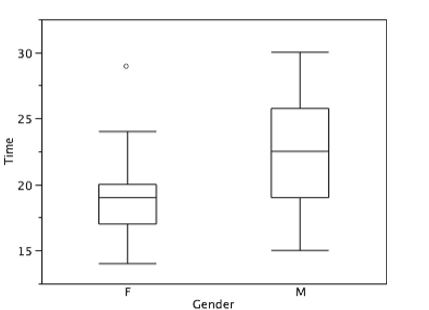
Aunque no dibujamos bigotes hasta valores externos o lejanos, todavía deseamos representarlos en nuestras parcelas de caja. Esto se logra agregando marcas adicionales más allá de los bigotes. Específicamente, los valores externos se indican con pequeñas “o” y los valores lejanos se indican con asteriscos (*). En nuestros datos, no hay valores lejanos y solo un valor externo. Este valor externo de 29 es para las mujeres y se muestra en la Figura\(\PageIndex{16}\).
Hay una marca más para incluir en las parcelas de caja (aunque a veces se omite). Indicamos la puntuación media para un grupo insertando un signo más. La figura\(\PageIndex{17}\) muestra el resultado de sumar medias a nuestras gráficas de caja.
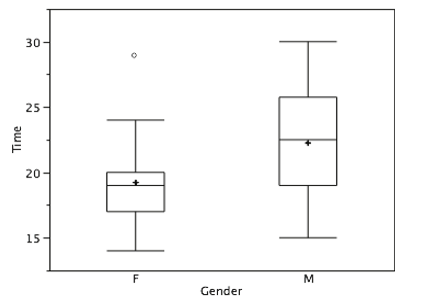
La figura\(\PageIndex{17}\) proporciona un resumen revelador de los datos. Dado que la mitad de las puntuaciones en una distribución están entre las bisagras (recordemos que las bisagras son los percentiles 25 y 75), vemos que la mitad de los tiempos femeninos están entre 17 y 20 segundos mientras que la mitad de los tiempos masculinos están entre 19 y 25.5 segundos. También vemos que las mujeres generalmente nombraban los colores más rápido que los hombres, aunque una mujer era más lenta que casi todos los hombres. La figura\(\PageIndex{18}\) muestra la gráfica de caja para los datos de las mujeres con etiquetas detalladas.
Las parcelas de caja proporcionan información básica sobre una distribución. Por ejemplo, una distribución con un sesgo positivo tendría un bigote más largo en la dirección positiva que en la dirección negativa. Una media mayor que la mediana también indicaría un sesgo positivo. Las parcelas de caja son buenas para retratar valores extremos y son especialmente buenas para mostrar diferencias entre distribuciones. Sin embargo, muchos de los detalles de una distribución no se revelan en una gráfica de caja y para examinar estos detalles se debe usar crear un histograma y/o una visualización de tallo y hoja.
Gráficos de barras
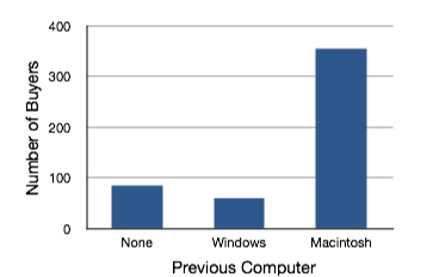
En la sección sobre variables cualitativas, vimos cómo se podían utilizar los gráficos de barras para ilustrar las frecuencias de diferentes categorías. Por ejemplo, el gráfico de barras que se\(\PageIndex{19}\) muestra en la Figura muestra cuántos compradores de computadoras iMac eran usuarios anteriores de Macintosh, usuarios anteriores de Windows y compradores de computadoras nuevas.
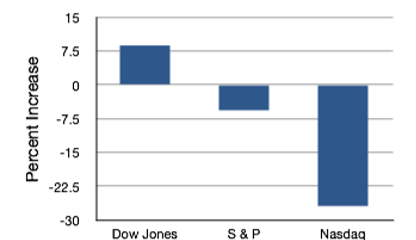
En esta sección mostramos cómo se pueden utilizar los gráficos de barras para presentar otro tipo de información cuantitativa, no solo los recuentos de frecuencia. El gráfico de barras de la Figura\(\PageIndex{20}\) muestra los incrementos porcentuales en los índices bursátiles Dow Jones, Standard and Poor 500 (S&P) y Nasdaq del 24 de mayo de 2000 al 24 de mayo de 2001. Observe que tanto el S & P como el Nasdaq tuvieron “incrementos negativos” lo que significa que disminuyeron de valor. En este gráfico de barras, el eje Y no es la frecuencia sino el incremento porcentual de cantidad firmada.
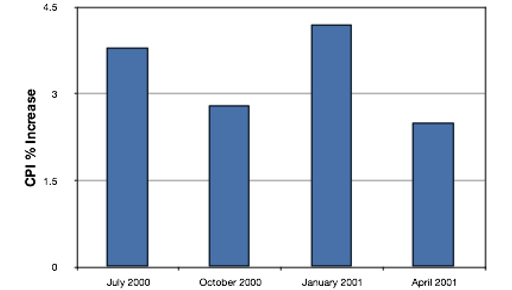
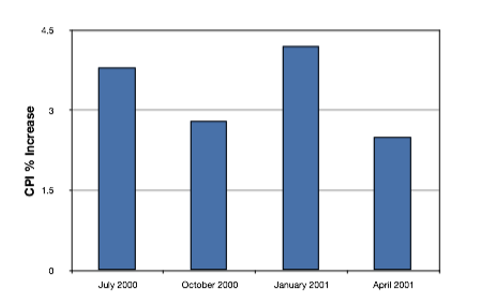
Los gráficos de barras son particularmente efectivos para mostrar los cambios a lo largo del tiempo. La figura\(\PageIndex{21}\), por ejemplo, muestra el incremento porcentual del Índice de Precios al Consumidor (IPC) en cuatro periodos de tres meses. La fluctuación de la inflación es evidente en la gráfica.
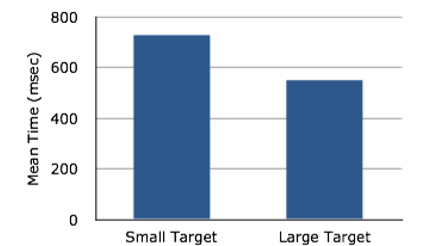
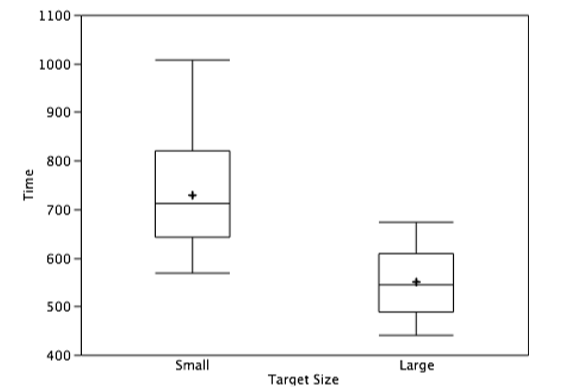
Los gráficos de barras se utilizan a menudo para comparar las medias de diferentes condiciones experimentales. La Figura 2.1.4 muestra el tiempo medio que le tomó a uno de nosotros (DL) mover el cursor a un objetivo pequeño o a un objetivo grande. En promedio, se requirió más tiempo para objetivos pequeños que para los grandes.
Aunque los gráficos de barras pueden mostrar medios, no los recomendamos para este propósito. En su lugar, se deben usar gráficas de caja ya que proporcionan más información que los gráficos de barras sin ocupar más espacio. Por ejemplo, en la Figura se muestra una gráfica de caja de los datos de movimiento del cursor\(\PageIndex{23}\). Se puede ver que Figura\(\PageIndex{23}\) revela más sobre la distribución de los tiempos de movimiento que Figura\(\PageIndex{22}\).
En la sección sobre variables cualitativas que se presentó anteriormente en este capítulo se discutió el uso de gráficos de barras para comparar distribuciones. También se notaron algunos errores gráficos comunes. La discusión anterior se aplica igualmente bien al uso de gráficos de barras para mostrar variables cuantitativas.
Gráficas de líneas
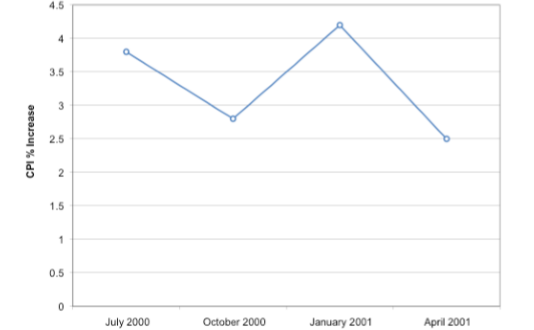
Un gráfico de líneas es un gráfico de barras con las partes superiores de las barras representadas por puntos unidos por líneas (el resto de la barra se suprime). Por ejemplo, la Figura\(\PageIndex{24}\) se presentó en la sección de gráficos de barras y muestra los cambios en el Índice de Precios al Consumidor (IPC) a lo largo del tiempo.
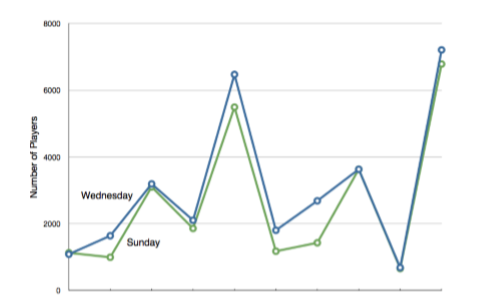
Un gráfico de líneas de estos mismos datos se muestra en la Figura\(\PageIndex{25}\). Si bien las cifras son similares, la gráfica lineal enfatiza el cambio de periodo a periodo.
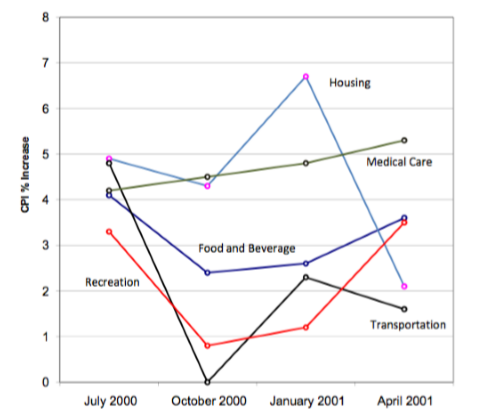
Los gráficos de líneas son apropiados solo cuando los ejes X e Y muestran variables ordenadas (en lugar de cualitativas). Aunque los gráficos de barras también se pueden usar en esta situación, los gráficos de líneas generalmente son mejores para comparar los cambios a lo largo del tiempo. La figura\(\PageIndex{26}\), por ejemplo, muestra incrementos porcentuales y disminuciones en cinco componentes del IPC. La cifra hace que sea fácil ver que los costos médicos tuvieron una progresión más constante que los otros componentes. Aunque se podría crear un gráfico de barras análogo, su interpretación no sería tan fácil.
Destacemos que es engañoso usar un gráfico de líneas cuando el eje X contiene variables meramente cualitativas. La figura muestra de\(\PageIndex{27}\) manera inapropiada una gráfica lineal de los datos del juego de cartas de Yahoo, discutidos en la sección sobre variables cualitativas. El defecto en la Figura\(\PageIndex{27}\) es que da la falsa impresión de que los juegos están naturalmente ordenados de manera numérica.
La forma de la distribución
Finalmente, es útil presentar una discusión sobre cómo describimos las formas de las distribuciones, que revisaremos en el siguiente capítulo para aprender cómo las diferentes formas afectan nuestros descriptores numéricos de datos y distribuciones.
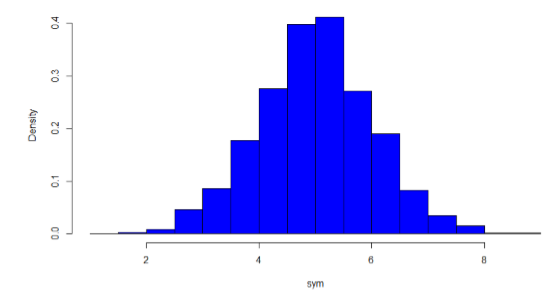
La característica principal que nos preocupa al evaluar la forma de una distribución es si la distribución es simétrica o sesgada. Una distribución simétrica, como su nombre indica, se puede cortar por el centro para formar 2 imágenes especulares. Aunque en la práctica nunca obtendremos una distribución perfectamente simétrica, nos gustaría que nuestros datos estuvieran lo más cerca posible de simétricos por razones en las que profundizamos en el Capítulo 3. Muchos tipos de distribuciones son simétricas, pero con mucho la distribución más común y pertinente en este punto es la distribución normal, mostrada en la Figura\(\PageIndex{28}\). Observe que aunque la simetría no es perfecta (por ejemplo, la barra justo a la derecha del centro es más alta que la que está justo a la izquierda), los dos lados tienen aproximadamente la misma forma. La distribución normal tiene un solo pico, conocido como el centro, y dos colas que se extienden por igual, formando lo que se conoce como forma de campana o curva de campana.
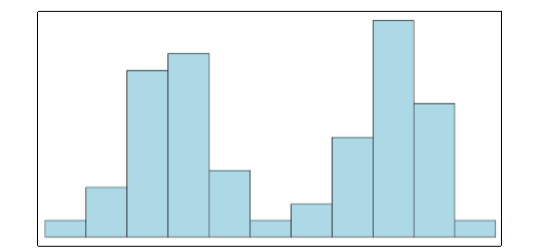
Las distribuciones simétricas también pueden tener múltiples picos. La figura\(\PageIndex{29}\) muestra una distribución bimodal, llamada así por los dos picos que se encuentran aproximadamente simétricamente a cada lado del punto central. Como veremos en el próximo capítulo, esta no es una característica particularmente deseable de nuestros datos y, peor aún, se trata de una característica relativamente difícil de detectar numéricamente. Por lo tanto, es importante visualizar sus datos antes de seguir adelante con cualquier análisis formal.
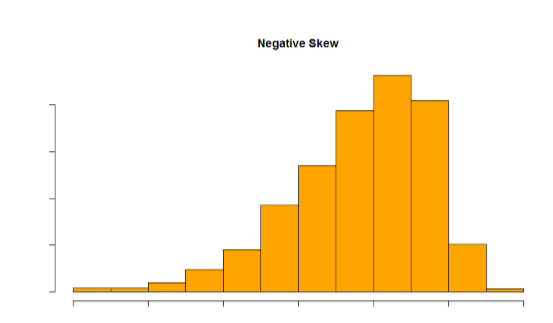
Las distribuciones que no son simétricas también vienen en muchas formas, más de las que se pueden describir aquí. La asimetría más común que se encuentra se conoce como sesgo, en la que una de las dos colas de la distribución es desproporcionadamente más larga que la otra. Esta propiedad puede afectar el valor de los promedios que utilizamos en nuestros análisis y convertirlos en una representación inexacta de nuestros datos, lo que causa muchos problemas.
El sesgo puede ser positivo o negativo (también conocido como derecha o izquierda, respectivamente), en función de qué cola es más larga. Es muy fácil confundir a los dos al principio; muchos estudiantes quieren describir el sesgo por donde se coloca la mayor parte de los datos (porción más grande del histograma, conocida como el cuerpo), pero la determinación correcta se basa en qué cola es más larga. Se puede pensar en la cola como una flecha: cualquiera que sea la dirección que apunte la flecha es la dirección del sesgo. Las cifras\(\PageIndex{30}\) y\(\PageIndex{31}\) muestran sesgo positivo (derecha) y negativo (izquierda), respectivamente.
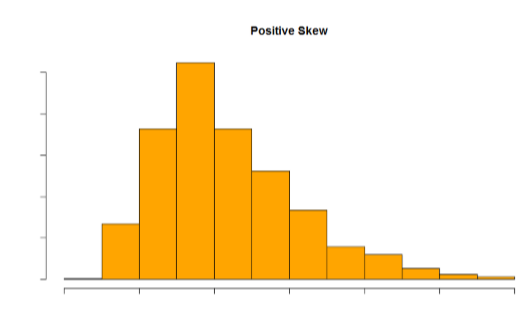
Figura\(\PageIndex{30}\): Una distribución sesgada positivamente.