2.E: Describir Datos usando Distribuciones y Gráficas (Ejercicios)
- Page ID
- 150651
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)
- Nombra algunas formas de graficar variables cuantitativas y algunas formas de graficar variables cualitativas.
- Respuesta:
-
Las variables cualitativas se muestran usando gráficos circulares y gráficos de barras. Las variables cuantitativas se muestran como diagramas de caja, histogramas, etc.
- Dados los siguientes datos, construya un gráfico circular y un gráfico de barras. ¿Cuál crees que es la forma más apropiada o útil de mostrar los datos?
| Género de película favorita | Frecuencia |
|---|---|
| Comedia | 14 |
| Terror | 9 |
| Romance | 8 |
| Acción | 12 |
- Finge que estás construyendo un histograma para describir la distribución de los salarios de las personas mayores de 40 años, pero que aún no están jubiladas.
- ¿Qué hay en el eje Y? Explique.
- ¿Qué hay en el eje X? Explique.
- ¿Cuál sería la forma probable de la distribución salarial? Explique por qué.
- Respuesta:
-
[No es necesario dibujar el histograma, solo describirlo a continuación]
- El eje Y tendría la frecuencia o proporción porque este es siempre el caso en los histogramas
- El eje X tiene ingresos, porque esta es la variable cuantitativa de interés
- Debido a que la mayoría de los datos de ingresos están sesgados positivamente, este histograma probablemente también estaría sesgado positivamente
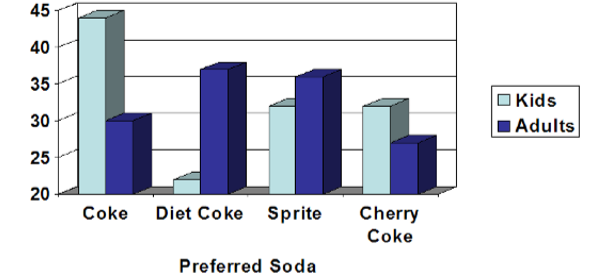
- A continuación aparece una gráfica que muestra el número de adultos y niños que prefieren cada tipo de refresco. Se encuestaron 130 adultos y niños. Discuta algunas formas en las que se podría mejorar la gráfica a continuación.
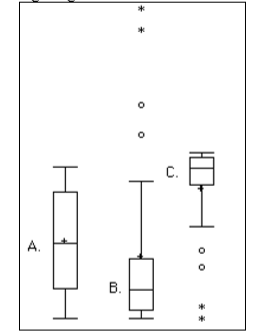
- ¿Cuál de las parcelas de caja en la gráfica tiene un gran sesgo positivo? ¿Cuál tiene un gran sesgo negativo?
- Respuesta:
-
El gráfico B tiene el sesgo positivo porque los valores atípicos (puntos y asteriscos) están en el extremo superior (superior); el gráfico C tiene el sesgo negativo porque los valores atípicos están en el extremo inferior.
- Cree un histograma de los siguientes datos que representen cuántos espectáculos los niños dijeron que ven cada día:
| Número de programas de TV | Frecuencia |
|---|---|
| 0 | 2 |
| 1 | 18 |
| 2 | 36 |
| 3 | 7 |
| 4 | 3 |
- Explicar las diferencias entre gráficos de barras e histogramas. ¿Cuándo se usaría cada uno?
- Respuesta:
-
En los gráficos de barras, las barras no se tocan; en los histogramas, las barras sí se tocan. Los gráficos de barras son apropiados para variables cualitativas, mientras que los histogramas son mejores para las variables cuantitativas.
- Dibuja un histograma de una distribución que sea
- Obsesgado negativamente
- Simétrico
- Positivamente sesgado
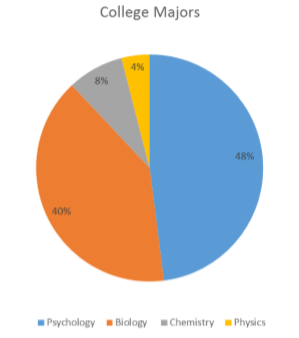
- Con base en el gráfico circular a continuación, que se hizo a partir de una muestra de 300 estudiantes, se construye una tabla de frecuencias de carreras universitarias.
- Respuesta:
-
Utilice el siguiente conjunto de datos para los cálculos a continuación:
Mayor Frecuencia Psicología 144 Biología 120 Química 24 Física 12
- Crear un histograma de los siguientes datos. Etiquete las colas y el cuerpo y determine si está sesgada (y dirección, si es así) o simétrica.
| Horas trabajadas por semana | Proporción |
|---|---|
| 0 -10 | 4 |
| 10 -20 | 8 |
| 20 - 30 | 11 |
| 30 - 40 | 51 |
| 40 - 50 | 12 |
| 50 - 60 | 9 |
| 60+ | 5 |