6.3: Uso de Error Estándar para Probabilidad
- Page ID
- 150857
Vimos en el capítulo 6 que podemos usar\(z\) -scores para dividir una distribución normal y calcular la proporción del área bajo la curva en una de las nuevas regiones, dándonos la probabilidad de seleccionar aleatoriamente una\(z\) -score en ese rango. Podemos seguir el proceso de muestreo exacto para las medias muestrales, convirtiéndolas en\(z\) -scores y calculando probabilidades. La única diferencia es que en lugar de dividir una puntuación bruta por la desviación estándar, dividimos la media de la muestra por el error estándar.
\[z=\dfrac{\overline{X}-\mu}{\sigma_{\overline{X}}}=\dfrac{\overline{X}-\mu}{\frac {\overline{\sigma}}{\sqrt{n}}} \]
Digamos que estamos dibujando muestras de una población con una media de 50 y desviación estándar de 10 (los mismos valores utilizados en la Figura 2). ¿Cuál es la probabilidad de que obtengamos una muestra aleatoria de tamaño 10 con una media mayor o igual a 55? Es decir, para n = 10, ¿cuál es la probabilidad de que\(\overline{X}\) ≥ 55? Primero, necesitamos convertir esta puntuación media de la muestra en una\(z\) puntuación -score:
\[z=\dfrac{55-50}{\frac{10}{\sqrt{10}}}=\dfrac{5}{3.16}=1.58 \nonumber \]
Ahora necesitamos sombrear el área bajo la curva normal correspondiente a puntuaciones mayores que\(z\) = 1.58 como en la Figura\(\PageIndex{1}\):
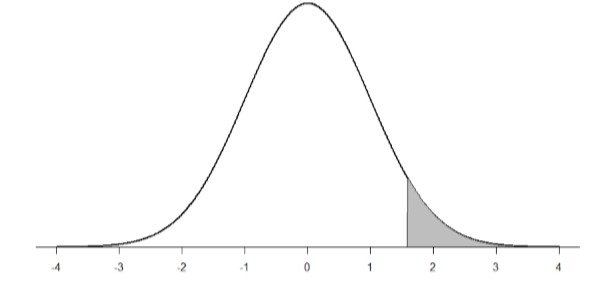
Ahora vamos a nuestra\(z\) -mesa y encontramos que el área a la izquierda de\(z\) = 1.58 es 0.9429. Finalmente, debido a que necesitamos el área a la derecha (según nuestro diagrama sombreado), simplemente restamos esto de 1 para obtener 1.00 — 0.9429 = 0.0571. Entonces, la probabilidad de sacar aleatoriamente una muestra de 10 personas de una población con una media de 50 y desviación estándar de 10 cuya media muestral es 55 o más es\(p\) = .0571, o 5.71%. Observe que estamos hablando de medios que son 55 o más. Eso se debe a que, estrictamente hablando, es imposible calcular la probabilidad de que una puntuación tome exactamente 1 valor ya que la “región sombreada” solo sería una línea sin área para calcular.
Ahora hagamos lo mismo, pero supongamos que en vez de solo tener una muestra de 10 personas tomamos una muestra de 50 personas. En primer lugar, encontramos\(z\):
\[z=\dfrac{55-50}{\frac{10}{\sqrt{50}}}=\dfrac{5}{1.41}=3.55 \]
Luego sombreamos la región apropiada de la distribución normal:
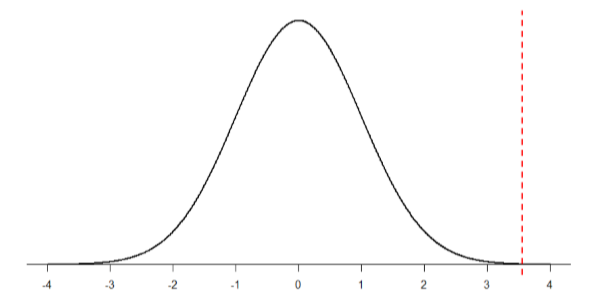
Observe que ninguna región de la Figura\(\PageIndex{2}\) parece estar sombreada. Eso se debe a que el área bajo la curva tan lejos en la cola es tan pequeña que ni siquiera se puede ver (se ha agregado la línea roja para mostrar exactamente dónde comienza la región). Así, ya sabemos que la probabilidad debe ser menor para\(N\) = 50 que\(N\) = 10 porque el tamaño del área (la proporción) es mucho menor.
Nos encontramos con un problema similar cuando tratamos de encontrar\(z\) = 3.55 en nuestra Tabla de Distribución Normal Estándar. El cuadro sólo sube a 3.09 porque todo más allá de eso es casi 0 y cambia tan poco que no vale la pena imprimir valores. Lo más cerca que podemos conseguir es restar el valor más grande, 0.9990, de 1 para obtener 0.001. Sabemos que, técnicamente, la probabilidad real es menor que esta (ya que 3.55 está más adentro de la cola que 3.09), por lo que decimos que la probabilidad es\(p\) < 0.001, o menor de 0.1%.
Este ejemplo muestra lo que puede tener un tamaño de muestra de impacto. De la misma población, buscando exactamente lo mismo, cambiar solo el tamaño de la muestra nos llevó de aproximadamente un 5% de probabilidad (o alrededor de 1/20 probabilidades) a una probabilidad menor de 0.1% (o menos de 1 en 1000). A medida que aumentaba el tamaño muestral n, el error estándar disminuyó, lo que\(z\) a su vez provocó que el valor de aumentara, lo que finalmente provocó que disminuyera el\(p\) valor -valor (término de probabilidad que usaremos mucho en la Unidad 2). Se puede pensar en esta relación como engranajes: girar la primera marcha (tamaño de muestra) en el sentido de las agujas del reloj hace que la siguiente marcha (error estándar) gire en sentido antihorario, lo que hace que la tercera marcha (z) gire en sentido horario, lo que finalmente hace que la última marcha (probabilidad) gire en sentido antihorario. Todas estas piezas encajan entre sí, y las relaciones siempre serán las mismas:
\[\mathrm{n} \uparrow \sigma_{\overline{X}} \downarrow \mathrm{z} \uparrow \mathrm{p} \downarrow\]
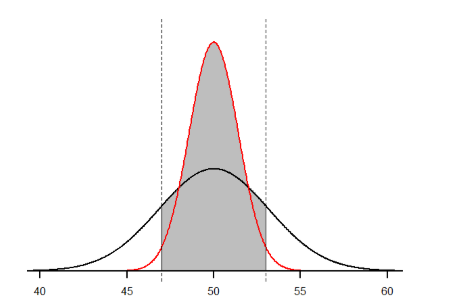
Veamos esto de una manera más. Para la misma población de tamaño de muestra 50 y desviación estándar 10, ¿qué proporción de medias muestrales caen entre 47 y 53 si son de tamaño de muestra 10 y tamaño de muestra 50?
Empezaremos de nuevo con\(n\) = 10. Al convertir 47 y 53 en\(z\) -puntuaciones, obtenemos\(z\) = -0.95 y\(z\) = 0.95, respectivamente. De nuestra\(z\) -tabla, encontramos que la proporción entre estas dos puntuaciones es de 0.6578 (el proceso aquí se deja fuera para que el alumno practique la conversión\(\overline{X}\) a\(z\) y\(z\) a proporciones). Entonces, 65.78% de las medias muestrales de tamaño muestral 10 caerán entre 47 y 53. Para\(n\) = 50, nuestros\(z\) -puntajes para 47 y 53 son ±2.13, lo que nos da una proporción del área como 0.9668, ¡casi 97%! Las regiones sombreadas para cada una de estas distribuciones de muestreo se muestran en la Figura\(\PageIndex{3}\). Las distribuciones de muestreo se muestran en la escala original, en lugar de como puntuaciones z, por lo que se puede ver el efecto del sombreado y cuánto del cuerpo cae dentro del rango, el cual está marcado con línea punteada.