6.2: La distribución de muestreo de las medias de la muestra
- Page ID
- 150856
Para ver cómo utilizamos el error de muestreo, aprenderemos sobre una nueva distribución teórica conocida como distribución muestral. De la misma manera que podemos reunir muchas partituras individuales y juntarlas para formar una distribución con un centro y untar, si tuviéramos que tomar muchas muestras, todas del mismo tamaño, y calcular la media de cada una de esas, podríamos juntar esos medios para formar una distribución. Esta nueva distribución es, intuitivamente, conocida como la distribución de medias muestrales. Es un ejemplo de lo que llamamos una distribución de muestreo, podemos estar formados a partir de un conjunto de cualquier estadística, como una media, una estadística de prueba, o un coeficiente de correlación (más sobre estos dos últimos en las Unidades 2 y 3). Para nuestros propósitos, comprender la distribución de las medias muestrales será suficiente para ver cómo funcionan todas las demás distribuciones de muestreo para habilitar e informar nuestros análisis inferenciales, por lo que estos dos términos se usarán indistintamente de aquí en adelante. Echemos un vistazo más profundo a algunas de sus características.
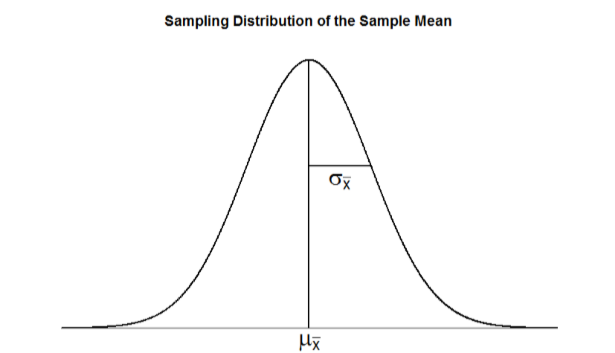
La distribución muestral de las medias muestrales se puede describir por su forma, centro y extensión, al igual que cualquiera de las otras distribuciones con las que hemos trabajado. La forma de nuestra distribución muestral es normal: una curva en forma de campana con un solo pico y dos colas que se extienden simétricamente en cualquier dirección, igual que lo que vimos en capítulos anteriores. El centro de la distribución muestral de las medias muestrales —que es, en sí misma, la media o promedio de las medias— es la verdadera media poblacional,\(μ\). Esto a veces se escribirá\(\mu_{\overline{X}}\) para denotarlo como la media de las medias de la muestra. La dispersión de la distribución de muestreo se denomina error estándar, se denota la cuantificación del error de muestreo\(\mu_{\overline{X}}\). La fórmula para el error estándar es:
\[\sigma_{\overline{X}}=\dfrac{\sigma}{\sqrt{n}} \]
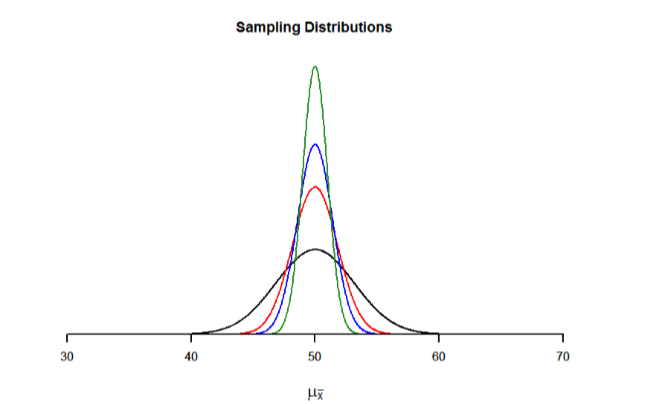
Observe que el tamaño de la muestra está en esta ecuación. Como se indicó anteriormente, la distribución muestral se refiere a muestras de un tamaño específico. Es decir, todas las medias muestrales deben calcularse a partir de muestras del mismo tamaño\(n\), tal\(n\) = 10,\(n\) = 30, o\(n\) = 100. Este tamaño de muestra se refiere a cuántas personas u observaciones hay en cada muestra individual, no cuántas muestras se utilizan para formar la distribución muestral. Esto se debe a que la distribución muestral es una distribución teórica, no una que jamás podamos calcular u observar. La figura\(\PageIndex{1}\) muestra los principios aquí expuestos en forma gráfica.
Dos Axiomas Importantes
Acabamos de aprender que la distribución muestral es teórica: en realidad nunca la vemos. Si eso es cierto, entonces ¿cómo podemos saber que funciona? ¿Cómo podemos usar algo que no vemos? La respuesta radica en dos hechos matemáticos muy importantes: el teorema del límite central y la ley de los grandes números. No vamos a entrar en las matemáticas detrás de cómo se derivaron estas afirmaciones, pero saber qué son y qué significan es importante para entender por qué funcionan las estadísticas inferenciales y cómo podemos sacar conclusiones sobre una población a partir de la información obtenida de una sola muestra.
Teorema de Límite Central
El teorema del límite central establece:
Para muestras de un solo tamaño\(n\), extraídas de una población con una media\(μ\) y varianza dadas\(σ^2\), la distribución muestral de medias muestrales tendrá una media\(\mu_{\overline{X}}=\mu\) y varianza\(\sigma _{X}^{2}=\dfrac{\sigma ^{2}}{n}\). Esta distribución se acercará a la normalidad a medida que\(n\) aumente.
A partir de esto, podemos encontrar la desviación estándar de nuestra distribución muestral, el error estándar. Como puede ver, al igual que cualquier otra desviación estándar, el error estándar es simplemente la raíz cuadrada de la varianza de la distribución.
La última frase del teorema del límite central establece que la distribución muestral será normal a medida que aumente el tamaño muestral de las muestras utilizadas para crearla. Lo que esto significa es que las muestras más grandes crearán una distribución más normal, por lo que somos más capaces de utilizar las técnicas que desarrollamos para distribuciones y probabilidades normales. Entonces, ¿qué tan grande es lo suficientemente grande? En general, una distribución de muestreo será normal si alguna de las dos características es verdadera:
- la población de la que se extraen las muestras se distribuye normalmente o
- el tamaño de la muestra es igual o mayor que 30.
Este segundo criterio es muy importante porque nos permite utilizar métodos desarrollados para distribuciones normales aunque la verdadera distribución de la población esté sesgada.
Ley de Grandes Números
La ley de números grandes simplemente establece que a medida que aumenta el tamaño de nuestra muestra, también aumenta la probabilidad de que nuestra media muestral sea una representación precisa de la verdadera media poblacional. Es la forma matemática formal de afirmar que las muestras más grandes son más precisas.
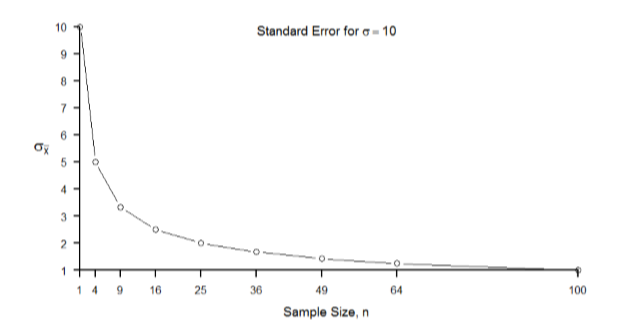
La ley de los grandes números está relacionada con el teorema del límite central, específicamente las fórmulas de varianza y error estándar. Observe que el tamaño de la muestra aparece en los denominadores de esas fórmulas. Un denominador mayor en cualquier fracción significa que el valor global de la fracción se vuelve más pequeño (es decir, 1/2 = 0.50, 1/3 — 0.33, 1/4 = 0.25, y así sucesivamente). Por lo tanto, los tamaños de muestra más grandes crearán errores estándar más pequeños. Ya sabemos que el error estándar es la dispersión de la distribución muestral y que una dispersión menor crea una distribución más estrecha. Por lo tanto, los tamaños de muestra más grandes crean distribuciones de muestreo más estrechas, lo que aumenta la probabilidad de que una media de la muestra esté cerca del centro y disminuye la probabilidad de que esté en las colas. Esto se ilustra en las Figuras\(\PageIndex{2}\) y\(\PageIndex{3}\).