8.1: El estadístico t
- Page ID
- 150813
En el último capítulo, se nos introdujo la prueba de hipótesis utilizando el\(z\) -estadístico para medias muestrales que aprendimos en la Unidad 1. Esta fue una manera útil de vincular el material y facilitarnos la nueva forma de mirar los datos, pero no es una prueba muy común porque se basa en conocer la desviación estándar de las poblaciones\(σ\), lo que rara vez va a ser el caso. En cambio, estimaremos ese parámetro\(σ\) usando el estadístico\(s\) de muestra de la misma manera que estimamos\(μ\) usando\(\overline{\mathrm{X}}\) (\(μ\)seguirá apareciendo en nuestras fórmulas porque sospechamos algo sobre su valor y eso es lo que estamos probando). Nuestro nuevo estadístico se llama\(t\), y para probar una media poblacional usando una sola muestra (llamada\(t\) prueba de 1 muestra) toma la forma:
\[t=\dfrac{\bar{X}-\mu}{s_{\bar{X}}}=\dfrac{\bar{X}-\mu}{s / \sqrt{n}} \]
Observe que\(t\) se ve casi idéntico a\(z\); esto se debe a que prueban exactamente lo mismo: el valor de una media muestral comparada con lo que esperamos de la población. La única diferencia es que ahora se denota el error estándar\(s_{\overline{\mathrm{X}}}\) para indicar que usamos el estadístico de muestra para la desviación estándar,\(s\), en lugar del parámetro de población\(σ\). El proceso de usar e interpretar el error estándar y el estadístico completo de prueba siguen siendo exactamente los mismos.
En el capítulo 3 aprendimos que las fórmulas para la desviación estándar de la muestra y la desviación estándar de la población difieren en un factor clave: el denominador para el parámetro es\(N\) pero el denominador para el estadístico es\(N – 1\), también conocido como grados de libertad,\(df\). Debido a que estamos usando una nueva medida de propagación, ya no podemos usar la distribución normal estándar y la\(z\) tabla -para encontrar nuestros valores críticos. Para\(t\) -tests, usaremos la\(t\) -distribution y\(t\) -table para encontrar estos valores.
La\(t\) -distribución, al igual que la distribución normal estándar, es simétrica y normalmente se distribuye con una media de 0 y un error estándar (como medida de desviación estándar para distribuciones de muestreo) de 1. Sin embargo, debido a que el cálculo del error estándar utiliza grados de libertad, habrá una distribución t diferente para cada grado de libertad. Por suerte, todos funcionan exactamente igual, por lo que en la práctica esta diferencia es menor.
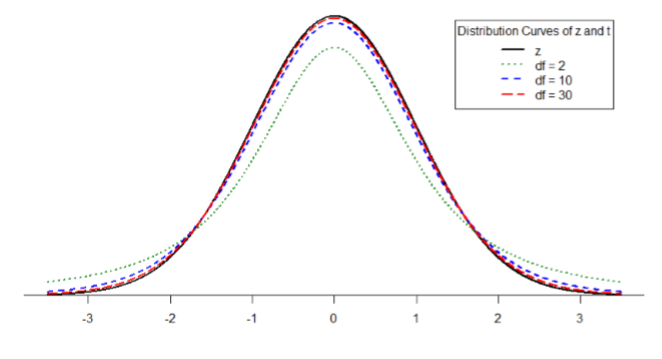
La figura\(\PageIndex{1}\) muestra cuatro curvas: una curva de distribución normal etiquetada\(z\) y tres curvas de distribución para 2, 10 y 30 grados de libertad. Dos cosas deben destacarse: Primero, para menores grados de libertad (e.g. 2), las colas de la distribución son mucho más gordas, es decir, la mayor proporción del área bajo la curva cae en la cola. Esto significa que tendremos que ir más lejos hacia la cola para cortar la porción correspondiente al 5% o\(α\) = 0.05, lo que a su vez conducirá a valores críticos más altos. Segundo, a medida que aumentan los grados de libertad, nos acercamos cada vez más a la\(z\) curva. Incluso la distribución con\(df\) = 30, correspondiente a un tamaño de muestra de apenas 31 personas, es casi indistinguible de\(z\). De hecho, una\(t\) -distribución con infinitos grados de libertad (teóricamente, por supuesto) es exactamente la distribución normal estándar. Debido a esto, la fila inferior de la\(t\) tabla -también incluye los valores críticos para\(z\) las pruebas en los niveles de significancia específicos. A pesar de que estas curvas son muy cercanas, sigue siendo importante usar la tabla correcta y los valores críticos, ya que las pequeñas diferencias pueden sumar rápidamente.
La tabla\(t\) -distribución enumera los valores críticos para pruebas de una y dos colas en varios niveles de significancia dispuestos en columnas. Las filas de la\(t\) tabla -lista grados de libertad hasta\(df\) = 100 con el fin de utilizar la curva de distribución apropiada. Sin embargo, no enumera todos los grados de libertad posibles en este rango, porque eso tomaría demasiadas filas. Arriba\(df\) = 40, las filas saltan en incrementos de 10. Si un problema requiere que encuentres valores críticos y no se enumeran los grados exactos de libertad, siempre redondeas al siguiente número más pequeño. Por ejemplo, si tienes 48 personas en tu muestra, los grados de libertad son\(N\) — 1 = 48 — 1 = 47; sin embargo, 47 no aparece en nuestra mesa, así que redondeamos hacia abajo y usamos los valores críticos para\(df\) = 40, aunque 50 esté más cerca. Hacemos esto porque evita inflar el Error Tipo I (falsos positivos, ver capítulo 7) mediante el uso de criterios que son demasiado laxos.


