8.2: Prueba de Hipótesis con t
- Page ID
- 150823
Las pruebas de hipótesis con la\(t\) estadística funcionan exactamente de la misma manera que\(z\) las pruebas, siguiendo el proceso de cuatro pasos de
- Afirmando la hipótesis
- Encontrar los valores críticos
- Computación del estadístico de prueba
- Tomando la Decisión.
Trabajaremos a través de un ejemplo: digamos que te mudas a una nueva ciudad y encuentras un taller de autos para cambiar tu aceite. Tu antiguo mecánico hizo el trabajo en unos 30 minutos (aunque nunca le prestaste la suficiente atención para saber cuánto variaba esa cantidad), y sospechas que tu nueva tienda tarda mucho más. Después de 4 cambios de aceite, crees que tienes pruebas suficientes para demostrarlo.
Paso 1: Indicar las Hipótesis Nuestras hipótesis para las pruebas t de 1 muestra son idénticas a las que utilizamos para\(z\) las pruebas. Seguimos declarando las hipótesis nulas y alternativas matemáticamente en términos del parámetro poblacional y escritas en inglés legible. Para nuestro ejemplo:
\(H_0\): No hay diferencia en el tiempo promedio para cambiar el aceite de un automóvil
\(H_0: μ = 30\)
\(H_A\): Esta tienda tarda más en cambiar el aceite que su antiguo mecánico
\(H_A: μ > 30\)
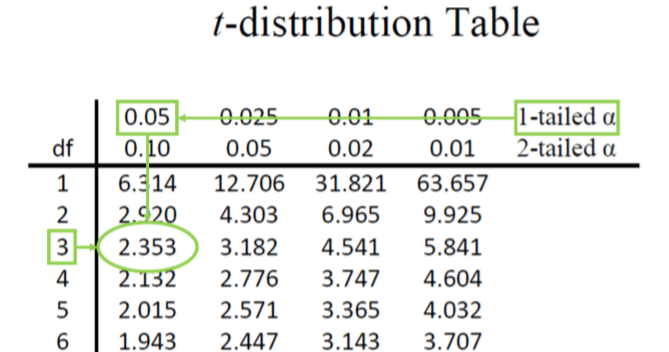
Paso 2: Encontrar los valores críticos Como se señaló anteriormente, nuestros valores críticos aún delinean el área en las colas bajo la curva correspondiente a nuestro nivel de significación elegido. Debido a que no tenemos ninguna razón para cambiar los niveles de significancia, usaremos\(α\) = 0.05, y debido a que sospechamos una dirección del efecto, tenemos una prueba de una cola. Para encontrar nuestros valores críticos para\(t\), necesitamos agregar una pieza más de información: los grados de libertad. Para este ejemplo:
\[df = N – 1 = 4 – 1 = 3 \nonumber \]
Al ir a nuestra\(t\) mesa, encontramos la columna correspondiente a nuestro nivel de significancia de una cola y encontramos dónde se cruza con la fila para 3 grados de libertad. Como se muestra en la Figura\(\PageIndex{1}\): nuestro valor crítico es\(t*\) = 2.353
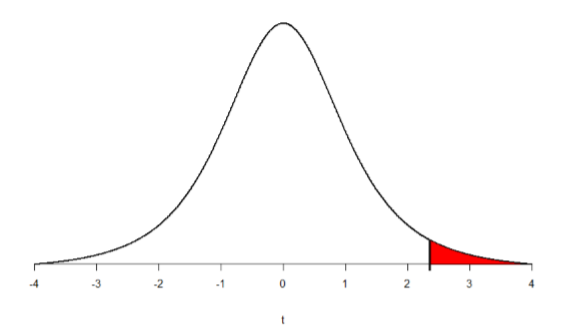
Luego podemos sombrear esta región en nuestra\(t\) distribución para visualizar nuestra región de rechazo
Paso 3: Calcular el estadístico de prueba Los cuatro tiempos de espera que experimentó para sus cambios de aceite son la nueva tienda fueron de 46 minutos, 58 minutos, 40 minutos y 71 minutos. Los usaremos para calcular\(\overline{\mathrm{X}}\) y s rellenando primero la tabla de suma de cuadrados en la Tabla\(\PageIndex{1}\):
| \(\overline{\mathrm{X}}\) | \(\mathrm{X}-\overline{\mathrm{X}}\) | \((\mathrm{X}-\overline{\mathrm{X}})^{2}\) |
|---|---|---|
| \ (\ overline {\ mathrm {X}}\) ">46 | \ (\ mathrm {X} -\ overline {\ mathrm {X}}\) ">-7.75 | \ ((\ mathrm {X} -\ overline {\ mathrm {X}}) ^ {2}\) ">60.06 |
| \ (\ overline {\ mathrm {X}}\) ">58 | \ (\ mathrm {X} -\ overline {\ mathrm {X}}\) ">4.25 | \ ((\ mathrm {X} -\ overline {\ mathrm {X}}) ^ {2}\) ">18.06 |
| \ (\ overline {\ mathrm {X}}\) ">40 | \ (\ mathrm {X} -\ overline {\ mathrm {X}}\) ">-13.75 | \ ((\ mathrm {X} -\ overline {\ mathrm {X}}) ^ {2}\) ">189.06 |
| \ (\ overline {\ mathrm {X}}\) ">71 | \ (\ mathrm {X} -\ overline {\ mathrm {X}}\) ">17.25 | \ ((\ mathrm {X} -\ overline {\ mathrm {X}}) ^ {2}\) ">297.56 |
| \ (\ overline {\ mathrm {X}}\) ">\(\Sigma\) =215 | \ (\ mathrm {X} -\ overline {\ mathrm {X}}\) ">\(\Sigma\) =0 | \ ((\ mathrm {X} -\ overline {\ mathrm {X}}) ^ {2}\) ">\(\Sigma\) =564.74 |
Después de rellenar la primera fila para obtener\(\Sigma\) =215, encontramos que la media es\(\overline{\mathrm{X}}\) = 53.75 (215 dividido por tamaño de muestra 4), lo que nos permite rellenar el resto de la tabla para obtener nuestra suma de cuadrados\(SS\) = 564.74, que luego conectamos a la fórmula para desviación estándar del capítulo 3:
\[s=\sqrt{\dfrac{\sum(X-\overline{X})^{2}}{N-1}}=\sqrt{\dfrac{S S}{d f}}=\sqrt{\dfrac{564.74}{3}}=13.72 \nonumber \]
A continuación, tomamos este valor y lo conectamos a la fórmula para el error estándar:
\[s_{\overline{X}}=\dfrac{s}{\sqrt{n}}=\dfrac{13.72}{2}=6.86 \nonumber \]
Y, finalmente, ponemos el error estándar, la media muestral y el valor de hipótesis nula en la fórmula para nuestro estadístico de prueba\(t\):
\[t=\dfrac{\overline{\mathrm{X}}-\mu}{s_{\overline{\mathrm{X}}}}=\dfrac{53.75-30}{6.86}=\dfrac{23.75}{6.68}=3.46 \nonumber \]
Esto puede parecer muchos pasos, pero en realidad es solo tomar nuestros datos brutos para calcular un valor a la vez y llevar ese valor hacia adelante a la siguiente ecuación: tamaño de la muestra de datos/grados de libertad media suma de cuadrados desviación estándar prueba estadística de error estándar. En cada paso, simplemente hacemos coincidir los símbolos de lo que acabamos de calcular a donde aparecen en la siguiente fórmula para asegurarnos de que estamos enchufando todo correctamente.
Paso 4: Tomar la decisión Ahora que tenemos nuestro valor crítico y la estadística de prueba, podemos tomar nuestra decisión utilizando los mismos criterios que usamos para una\(z\) prueba -. Nuestro\(t\) estadístico obtenido fue\(t\) = 3.46 y nuestro valor crítico fue\(t* = 2.353: t > t*\), por lo que rechazamos la hipótesis nula y concluimos:
Con base en nuestros cuatro cambios de aceite, el nuevo mecánico tarda más en promedio (\(\overline{\mathrm{X}}\)= 53.75) en cambiar el aceite que nuestro antiguo mecánico,\(t(3)\) = 3.46,\(p\) < .05.
Observe que también incluimos los grados de libertad entre paréntesis junto a\(t\). Y debido a que encontramos un resultado significativo, necesitamos calcular un tamaño de efecto, que sigue siendo el de Cohen\(d\), pero ahora usamos\(s\) en lugar de\(σ\):
\[d=\dfrac{\overline{X}-\mu}{s}=\dfrac{53.75-30.00}{13.72}=1.73 \nonumber \]
Este es un gran efecto. También hay que señalar que para algunas cosas, como los minutos en nuestro ejemplo actual, también podemos interpretar la magnitud de la diferencia que observamos (23 minutos y 45 segundos) como un indicador de importancia ya que el tiempo es una métrica familiar.


