9.3: Aumento de la Satisfacción en el Trabajo
- Page ID
- 151023
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Los trabajadores de una empresa local se han quejado de que las condiciones de trabajo se han vuelto muy malas, las horas son demasiado largas y no se sienten apoyados por la dirección. La compañía contrata a un consultor para que venga y ayude a solucionar la situación antes de que se ponga tan mal que los empleados empiecen a dejar de fumar. El consultor primero evalúa 40 del nivel de satisfacción laboral del empleado como parte de los grupos focales utilizados para identificar cambios específicos que podrían ayudar. La compañía instituye algunos de estos cambios, y seis meses después el consultor regresa para medir nuevamente la satisfacción laboral. Sabiendo que algunas intervenciones pierden la marca y en realidad pueden empeorar las cosas, el consultor prueba una diferencia en cualquier dirección (es decir, aumentar o disminuir en la satisfacción laboral promedio) en el nivel\(α\) = 0.05 de significancia.
Paso 1: Declarar las Hipótesis Primero, declaramos nuestras hipótesis nulas y alternativas:
\(H_0\): No hay cambio en la satisfacción laboral promedio
\(H_0: μD = 0\)
\(H_A\): Hay un incremento en la satisfacción laboral promedio
\(H_A: μD > 0\)
En este caso, esperamos que los cambios que hicimos mejoren la satisfacción de los empleados y, debido a que basamos los cambios en las recomendaciones de los empleados, tenemos buenas razones para creer que lo harán. Así, utilizaremos una hipótesis alternativa unidireccional.
Paso 2: Encontrar los Valores Críticos Nuestros valores críticos volverán a estar basados en nuestro nivel de significación, que sabemos es\(α\) = 0.05, la direccionalidad de nuestra prueba, que es de una cola a la derecha, y nuestros grados de libertad. Para nuestra\(t\) prueba de muestras dependientes, los grados de libertad aún se dan como\(df = n – 1\). Para este problema, tenemos 40 personas, por lo que nuestros grados de libertad son 39. Al ir a nuestra tabla t, encontramos que el valor crítico es\(t*\) = 1.685 como se muestra en la Figura\(\PageIndex{1}\).
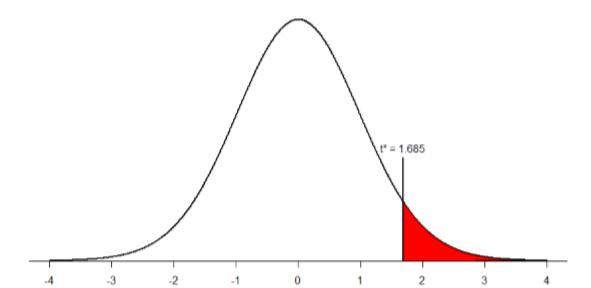
Paso 3: Calcular el estadístico de prueba Ahora que se establecen los criterios, es el momento de calcular el estadístico de prueba. Los datos obtenidos por el consultor encontraron que las puntuaciones de diferencia del tiempo 1 al tiempo 2 tuvieron una media de\(\overline{\mathrm{X}_{\mathrm{D}}}\) = 2.96 y una desviación estándar de\(s_D\) = 2.85. Usando esta información, más el tamaño de la muestra (\(N\)= 40), primero calculamos el error estándar:
\[s_{\overline{x_{D}}}=s_{D / \sqrt{n}}=2.85 / \sqrt{40}=2.85 / 6.32=0.46 \nonumber \]
Ahora, podemos poner ese valor, junto con nuestra media muestral y valor de hipótesis nula, en la fórmula para\(t\) y calcular el estadístico de prueba:
\[t=\dfrac{\overline{X_{D}}-\mu_{D}}{s_{\overline{X}_{D}}}=\dfrac{2.96-0}{0.46}=6.43 \nonumber \]
Observe que, debido a que el valor de hipótesis nula de una\(t\) prueba de muestras dependientes es siempre 0, simplemente podemos dividir nuestra media de muestra obtenida por el error estándar.
Paso 4: Tomar la Decisión Hemos obtenido un estadístico de prueba de\(t\) = 6.43 que podemos comparar con nuestro valor crítico previamente establecido de\(t*\) = 1.685. 6.43 es mayor que 1.685, así\(t > t*\) y rechazamos la hipótesis nula:
Rechazar\(H_0\). Con base en los datos de muestra de 40 trabajadores, podemos decir que la intervención mejoró estadísticamente significativamente la satisfacción laboral (\(\overline{\mathrm{X}_{\mathrm{D}}}\)= 2.96) entre los trabajadores,\(t(39) = 6.43\),\(p < 0.05\).
Debido a que este resultado fue estadísticamente significativo, vamos a querer calcular Cohen\(d\) como tamaño de efecto usando el mismo formato que hicimos para la\(t\) última prueba:
\[t=\dfrac{\overline{X_{D}}-\mu_{D}}{s_{D}}=\dfrac{2.96}{2.85}=1.04 \nonumber \]
Este es un tamaño de efecto grande. Observe nuevamente que aquí podemos omitir el valor de hipótesis nula porque siempre es igual a 0.
Ojalá el ejemplo anterior dejara claro que ejecutar una\(t\) prueba de muestras dependientes para buscar diferencias antes y después de algún tratamiento funciona exactamente de la misma manera que lo hace una\(t\) prueba regular de 1 muestra, lo que fue solo un pequeño cambio en la forma en que se realizaron\(z\) las pruebas en el capítulo 7. En este punto, este proceso debería ser familiar, y seguiremos haciendo pequeños ajustes a este proceso familiar a medida que nos encontremos con nuevos tipos de datos para probar nuevos tipos de preguntas de investigación.


