13.2: Predicción

El objetivo de la regresión es el mismo que el objetivo del ANOVA: tomar lo que sabemos de una variable (\(X\)) y usarlo para explicar nuestras diferencias observadas en otra variable (\(Y\)). En ANOVA, hablamos —y probamos— diferencias de medias grupales, pero en regresión no tenemos grupos para nuestra variable explicativa; tenemos una variable continua, como en correlación. Debido a esto, nuestro vocabulario será un poco diferente, pero el proceso, la lógica y el resultado final son todos iguales.

En regresión, hablamos con mayor frecuencia de predicción, específicamente predecir nuestra variable de resultado\(Y\) a partir de nuestra variable explicativa\(X\), y usamos la línea de mejor ajuste para hacer nuestras predicciones. Echemos un vistazo a la ecuación para la línea, que es bastante simple:

\[\widehat{\mathrm{Y}}=\mathrm{a}+\mathrm{bX} \]

Los términos en la ecuación se definen como:

• \(\widehat{\mathrm{Y}}\): el valor predicho de\(Y\) para una persona individual
• \(a\): la intercepción de la línea
• \(b\): la pendiente de la línea
• \(X\): el valor observado de\(X\) para una persona individual

Lo que esto nos muestra es que usaremos nuestro valor conocido de\(X\) para cada persona para predecir el valor de\(Y\) para esa persona. El valor predicho,\(\widehat{\mathrm{Y}}\), se llama “\(y\)-hat” y es nuestra mejor suposición para cuál es la puntuación de una persona en el resultado. Observe también que la forma de la ecuación es muy similar a las ecuaciones lineales muy simples que probablemente haya encontrado antes y solo tiene dos estimaciones de parámetros: una intersección (donde la línea cruza el eje Y) y una pendiente (qué tan empinada —y la dirección, positiva o negativa— es la línea). Estas son estimaciones de parámetros porque, como todo lo demás en la estadística, nos interesa aproximar el verdadero valor de la relación en la población pero solo podemos estimarla utilizando datos de muestra. Pronto veremos que uno de estos parámetros, la pendiente, es el foco de nuestras pruebas de hipótesis (la intercepción solo está ahí para hacer que las matemáticas funcionen correctamente y rara vez es interpretable). Las fórmulas para estas estimaciones de parámetros utilizan valores muy familiares:

\[\mathrm{a}=\overline{\mathrm{Y}}-\mathrm{b} \overline{\mathrm{X}} \]

\[\mathrm{b}=\dfrac{\operatorname{cov}_{X Y}}{s_{X}^{2}}=\dfrac{S P}{S S X}=r\left(\dfrac{S_{y}}{s_{x}}\right) \]

Ya hemos visto cada uno de estos antes. \(\overline{Y}\)y\(\overline{X}\) son la media de\(Y\) y\(X\), respectivamente;\(\operatorname{cov}_{X Y}\) es la covarianza de\(X\) y\(Y\) aprendimos sobre con correlaciones; y\(s_{X}^{2}\) es la varianza de\(X\). La fórmula para la pendiente es muy similar a la fórmula para un coeficiente de correlación de Pearson; la única diferencia es que estamos dividiendo por la varianza de\(X\) en lugar del producto de las desviaciones estándar de\(X\) y\(Y\). Debido a esto, nuestra pendiente se escala a la misma escala que nuestra\(X\) variable y ya no se limita a estar entre 0 y 1 en valor absoluto. Esta fórmula proporciona una definición clara de la pendiente de la línea de mejor ajuste, y al igual que con la correlación, esta fórmula de definición se puede simplificar en una fórmula computacional corta para facilitar los cálculos. En este caso, simplemente estamos tomando la suma de productos y dividiendo por la suma de cuadrados para\(X\).

Observe que existe una tercera fórmula para la pendiente de la línea que implica la correlación entre\(X\) y\(Y\). Esto se debe a que la regresión y la correlación buscan lo mismo: una línea recta a través de la mitad de los datos. La única diferencia entre un coeficiente de regresión en regresión lineal simple y un coeficiente de correlación de Pearson es la escala. Entonces, si te faltan datos brutos pero tienes información resumida sobre la correlación y las desviaciones estándar para las variables, aún puedes calcular una pendiente, y por lo tanto interceptar, para una línea de mejor ajuste.

Es muy importante señalar que\(Y\) los valores en las ecuaciones para\(a\) y\(b\) son nuestros\(Y\) valores observados en el conjunto de datos, NO los\(Y\) valores predichos (\(\widehat{\mathrm{Y}}\)) de nuestra ecuación para la línea de mejor ajuste. Así, tendremos 3 valores para cada persona: el valor observado de\(X (X)\), el valor observado de\(Y (Y)\), y el valor predicho de\(Y (\widehat{\mathrm{Y}}\)). Quizás se esté preguntando por qué trataríamos de predecir\(Y\) si tenemos un valor observado de\(Y\), y esa es una pregunta muy razonable. La respuesta tiene dos explicaciones: primero, necesitamos usar valores conocidos de\(Y\) para calcular las estimaciones de parámetros en nuestra ecuación, y usamos la diferencia entre nuestros valores observados y valores predichos (\(Y – \widehat{\mathrm{Y}}\)) para ver qué tan precisa es nuestra ecuación; segundo, a menudo usamos regresión para crear un modelo predictivo que luego podemos usar para predecir valores de\(Y\) para otras personas para las que solo tenemos información\(X\).

Veamos esto a partir de un ejemplo aplicado. Las empresas suelen tener más aspirantes a un empleo que tienen vacantes disponibles, por lo que quieren saber quién de los aspirantes es más probable que sea el mejor empleado. Hay muchos criterios que se pueden utilizar, pero uno es un test de personalidad para la conciencia, con la creencia de que los empleados más concienzudos (más responsables) son mejores que los empleados menos concienzudos. Una empresa podría dar a sus empleados un inventario de personalidad para evaluar la conciencia y los datos de desempeño existentes para buscar una relación. En este ejemplo, hemos conocido valores del predictor (\(X\), escrupulosidad) y resultado (\(Y\), desempeño laboral), por lo que podemos estimar una ecuación para una línea de mejor ajuste y ver con qué precisión concienzudo predice el desempeño laboral, luego usar esta ecuación para predecir el desempeño laboral futuro de aspirantes basados únicamente en sus valores conocidos de conciencia a partir de los inventarios de personalidad dados durante el proceso de solicitud.

La clave para evaluar si una regresión lineal funciona bien es la diferencia entre nuestros\(Y\) valores observados y conocidos y nuestros\(\widehat{\mathrm{Y}}\) valores predichos. Como se mencionó al pasar anteriormente, utilizamos la resta para encontrar la diferencia entre ellos (\(Y – \widehat{\mathrm{Y}}\)) de la misma manera que usamos la resta para puntuaciones de desviación y sumas de cuadrados. El valor (\(Y – \widehat{\mathrm{Y}}\)) es nuestro residual, que, como se definió anteriormente, es lo cerca que está nuestra línea de mejor ajuste a nuestros valores reales. Podemos visualizar los residuos para tener una mejor idea de lo que son creando una gráfica de dispersión y superponiendo una línea de mejor ajuste sobre ella, como se muestra en la Figura\(\PageIndex{1}\).

Figura\(\PageIndex{1}\): Gráfica de dispersión con residuos.

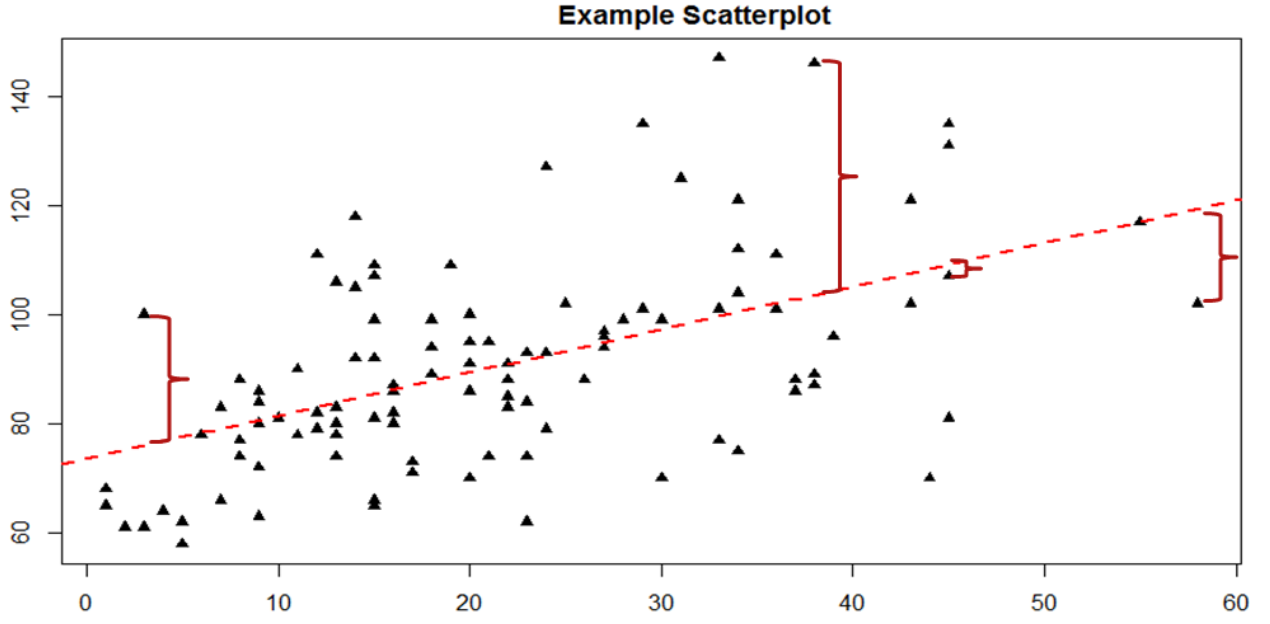
En la Figura\(\PageIndex{1}\), los puntos triangulares representan observaciones de cada persona en ambos\(X\)\(Y\) y la línea discontinua de color rojo brillante es la línea de mejor ajuste estimada por la ecuación\(\widehat{\mathrm{Y}}= a + bX\). Para cada persona en el conjunto de datos, la línea representa su puntaje predicho. El corchete rojo oscuro entre los puntos triangulares y las puntuaciones predichas en la línea de mejor ajuste son nuestros residuales (solo se dibujan para cuatro observaciones para facilitar la visualización, pero en realidad hay uno para cada observación); se puede ver que algunos residuos son positivos y algunos son negativos, y que algunos son muy grandes y algunas son muy pequeñas. Esto significa que algunas predicciones son muy precisas y algunas son muy inexactas, y algunas predicciones sobreestiman valores y algunos valores subestimados. En todo el conjunto de datos, la línea de mejor ajuste es la que minimiza el valor total (suma) de todos los residuos. Es decir, aunque las predicciones a nivel individual pueden ser algo inexactas, a lo largo de nuestra muestra completa y (teóricamente) en muestras futuras nuestra cantidad total de error es lo más pequeña posible. Llamamos a esta propiedad de la línea de mejor ajuste la Solución de Error de Mínimos Cuadrados. Este término significa que la solución —o ecuación— de la línea es la que proporciona el menor valor posible de los errores al cuadrado (al cuadrado para que se puedan sumar, al igual que en la desviación estándar) en relación con cualquier otra línea recta que pudiéramos dibujar a través de los datos.

Predicción de puntajes y explicación de varianza

Ahora hemos visto que el propósito de la regresión es doble: queremos predecir puntajes basados en nuestra línea y, como se dijo anteriormente, explicar la varianza en nuestra\(Y\) variable observada al igual que en ANOVA. Estos dos propósitos van de la mano, y nuestra capacidad para predecir puntuaciones es literalmente nuestra capacidad para explicar la varianza. Es decir, si no podemos dar cuenta de la varianza en\(Y\) base a\(X\), entonces no tenemos ninguna razón para usar\(X\) para predecir valores futuros de\(Y\).

Sabemos que la varianza general en\(Y\) es una función de cada puntaje que se desvía de la media de\(Y\) (como en nuestro cálculo de varianza y desviación estándar). Entonces, al igual que los corchetes rojos en la figura 1 que representan los residuos, dados como (\(Y – \widehat{\mathrm{Y}}\)), podemos visualizar la varianza general como la distancia de cada puntaje desde la media general de\(Y\), dada como (\(Y – \overline{Y}\)), nuestra puntuación de desviación normal. Esto se muestra en la Figura\(\PageIndex{2}\).

Figura\(\PageIndex{2}\): Gráfica de dispersión con residuos y puntuaciones de desviación.

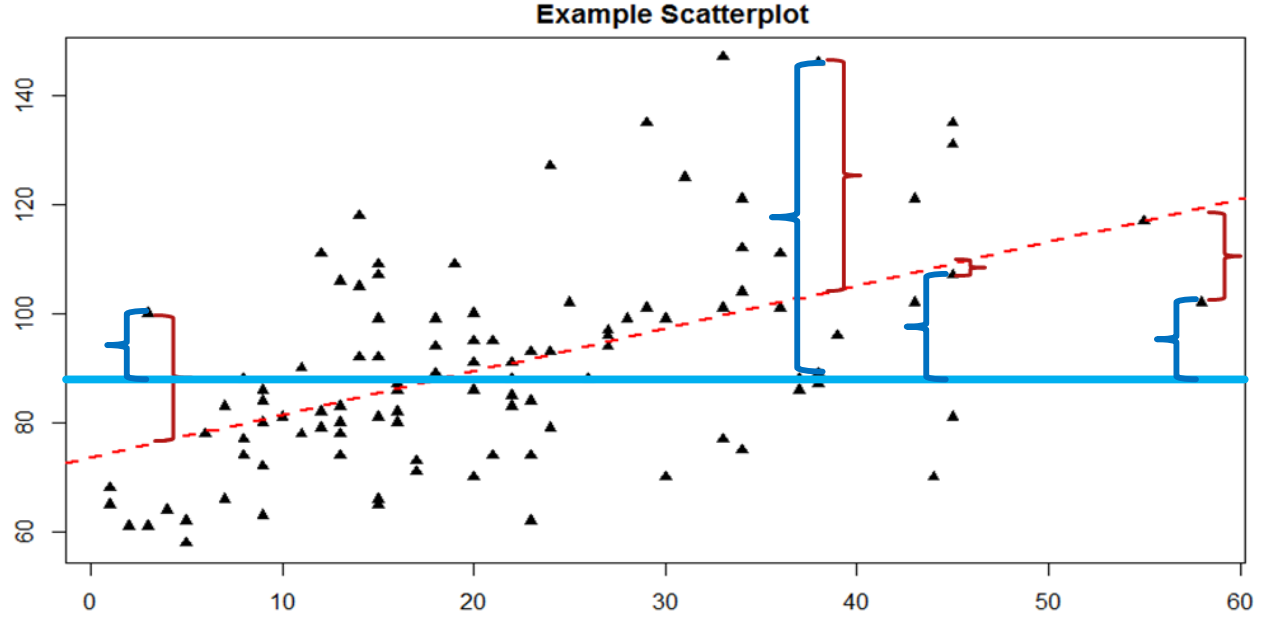
En la Figura\(\PageIndex{2}\), la línea azul sólida es la media de\(Y\), y los corchetes azules son las puntuaciones de desviación entre nuestros valores observados de\(Y\) y la media de\(Y\). Esto representa la varianza general que estamos tratando de explicar. Así, los residuales y las puntuaciones de desviación son el mismo tipo de idea: la distancia entre una puntuación observada y una línea dada, ya sea la línea de mejor ajuste que da predicciones o la línea que representa la media que sirve como línea base. La diferencia entre estos dos valores, que es la distancia entre las propias líneas, es la capacidad de nuestro modelo para predecir puntuaciones por encima y más allá de la media basal; es decir, es la capacidad de nuestros modelos para explicar la varianza que observamos en\(Y\) base a valores de\(X\). Si no tenemos capacidad para explicar varianza, entonces nuestra línea será plana (la pendiente será 0.00) y será la misma que la línea que representa la media, y la distancia entre las líneas será 0.00 también.

Ahora tenemos tres datos: la distancia desde la puntuación observada hasta la media, la distancia desde la puntuación observada hasta la línea de predicción, y la distancia desde la línea de predicción hasta la media. Estas son nuestras tres piezas de información necesarias para probar nuestras hipótesis sobre regresión y calcular los tamaños de los efectos. Son nuestras tres Sumas de Cuadrados, al igual que en ANOVA. Nuestra distancia desde la puntuación observada hasta la media es la Suma de Cuadrados Total, que estamos tratando de explicar. Nuestra distancia desde la puntuación observada hasta la línea de predicción es nuestro Error de Suma de Cuadrados, o residual, que estamos tratando de minimizar. Nuestra distancia desde la línea de predicción hasta la media es nuestro Modelo de Suma de Cuadrados, que es nuestro efecto observado y nuestra capacidad para explicar la varianza. Cada uno de estos irá a la tabla ANOVA para calcular nuestro estadístico de prueba.