Resolver ecuaciones lineales en una variable

Última actualización
Guardar como PDF

Page ID: 149384

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Resultados de aprendizaje

Resolver ecuaciones lineales para la variable.

Es una tarea común en álgebra resolver una ecuación para una variable. El objetivo será obtener la variable en un lado de la ecuación por sí sola y que el otro lado de la ecuación solo sea un número. El proceso implicará identificar las operaciones que se realizan sobre la variable y aplicar la operación inversa a ambos lados de la ecuación. Esto se gestionará a la inversa del orden de operaciones.

Ejemplo$\PageIndex{1}$

Resuelve la siguiente ecuación para$x$.

\[3x+4=11 \label{EQ1.1}\]

Solución

Comenzamos por mirar las operaciones que se realizan para$x$, haciendo un seguimiento del orden. La primera operación es “multiplicar por 3" y la segunda es “sumar 4". Ahora hacemos todo al revés. Dado que la última operación es “sumar 4", nuestro primer paso es restar 4 de ambos lados de la Ecuación\ ref {EQ1.1}.

\[3x \cancel{+ 4} \color{Cerulean}{ \cancel{-4}} \color{black} =11 \color{Cerulean}{ -4} \nonumber\]

lo que simplifica la ecuación

\[3x = 7 \nonumber\]

A continuación, la forma de deshacer “multiplicar por 3" es dividir ambos lados por 3. Obtenemos

\[ \dfrac{\cancel{3}x}{\color{Cerulean}{\cancel{3}}} \color{black}= \dfrac{7}{\color{Cerulean}{3}} \nonumber\]

\[x=\dfrac{7}{3} \nonumber\]

Ejemplo$\PageIndex{2}$

El rectángulo de arriba es un diagrama para una distribución uniforme del 2 al 9 que pide el primer cuartil. El área del rectángulo rojo más pequeño que tiene base de 2 a Q1 y altura 1/7 es 1/4. Encuentra Q1.

Solución

Comenzamos usando la fórmula de área para un rectángulo:

\[\text{Area} = \text{Base} \times \text{Height} \label{EQ1}\]

Contamos con:

Área =$\frac{1}{4}$
Base =$Q1-2$
Altura =$\frac{1}{7}$

Conecte esto a la Ecuación\ ref {EQ1} para obtener:

\[\frac{1}{4}=\left(Q1-2\right)\left(\frac{1}{7}\right) \label{EQ2}\]

Tenemos que resolver para$Q1$. Primero multiplica ambos lados de la Ecuación\ ref {EQ2} por 7 para obtener:

\[ \begin{align} \color{Cerulean}{7} \color{black} \left(\dfrac{1}{4}\right) &= \color{Cerulean}{\cancel{7}} \color{black} \left(Q1-2\right) \cancel{ \left(\frac{1}{7}\right)} \nonumber \\[5pt] \dfrac{7}{4} &=Q1-2 \label{EQ4} \end{align}\]

Ahora agregue 2 a ambos lados de la Ecuación\ ref {EQ4} para obtener:

\[ \begin{align*} \dfrac{7}{4} \color{Cerulean} +2 \color{black} & =Q1 \cancel{-2} \color{Cerulean}{\cancel{+2}} \\[5pt] \dfrac{7}{4}+2&=Q1 \end{align*}\]

\[Q1=\frac{7}{4}+2 \nonumber\]

Poner esto en una calculadora da:

\[Q1=3.75 \nonumber\]

Ejemplo$\PageIndex{3}$: z-score

La puntuación z para un valor dado$x$ para una distribución con media poblacional$\mu $ y desviación estándar poblacional$\sigma $ viene dada por:

\[z=\frac{x-\mu}{\sigma} \nonumber\]

Un minorista en línea ha encontrado que la media de ventas de la población por día es de $2,841 y la desviación estándar de la población es de $895. Un valor de$x$ se considera un valor atípico si la puntuación z es menor que -2 o mayor que 2. ¿Cuántas ventas se deben realizar para tener un puntaje z de 2?

Solución

Primero identificamos cada una de las variables dadas. Dado que la media poblacional es de 2,841, tenemos:

\[\mu=2841 \nonumber \]

Se nos dice que la desviación estándar poblacional es de 895 metros, por lo que:

\[\sigma=895 \nonumber \]

También se nos da que la puntuación z es 2, de ahí:

\[z=2 \nonumber \]

Ahora ponemos los números en la fórmula para que el puntaje z obtenga:

\[2=\frac{x-2841}{895} \nonumber \]

A continuación podemos cambiar el orden de la ecuación para que el$x$ esté en el lado izquierdo de la ecuación:

\[\frac{x-2841}{895}=2 \nonumber \]

A continuación, resolvemos para$x$. Primero multiplica ambos lados de la ecuación por 895 para obtener

\[x-2841=2\left(895\right)=1790 \nonumber \]

Finalmente, podemos sumar 2841 a ambos lados de la ecuación para obtener$x$ por sí mismo:

\[x=1790+2841=4631 \nonumber \]

Podemos concluir que si las ventas del día están en 4631 dólares, el puntaje z es 2.

Ejercicio

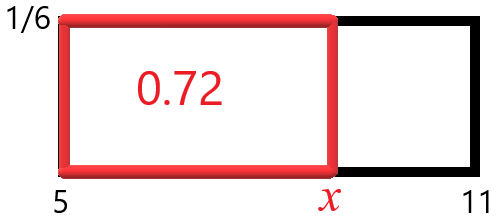
El rectángulo de abajo es un diagrama para una distribución uniforme del 5 al 11 que pide el percentil ⁷². El área del rectángulo rojo más pequeño que tiene base del 5 al percentil ⁷²$x$, y la altura 1/6 es 0.72. Encuentra$x$.

rectángulo: base exterior 5 a 11, base interior 5 a x, altura 1/6