10.7: Error Tipo II y Poder Estadístico
- Page ID
- 151749
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)En el ejemplo anterior, el estadístico no logró rechazar la Hipótesis Null debido a que la probabilidad de cometer un error de Tipo I (rechazar una verdadera Hipótesis Null) excedió el nivel de significancia de 5%. Sin embargo, el estadístico podría haber cometido un error Tipo II si la máquina realmente está funcionando incorrectamente. Una de las tareas importantes y muchas veces pasadas por alto es analizar la probabilidad de cometer el error Tipo II (\(\beta\)). Por lo general, los estadísticos miran el poder estadístico que es el complemento de\(\beta\).
Beta (\(\beta\)): La probabilidad de no rechazar la hipótesis nula cuando en realidad es falsa.
Poder (o Poder Estadístico): La probabilidad de rechazar la hipótesis nula cuando en realidad es falsa.
Tanto la beta como la potencia se calculan para valores específicos posibles de la Hipótesis Alternativa.
| No Rechazar\(H_o\) | Rechazar\(H_o\) | |
| \(H_o\)es verdad | \(1-\alpha\) | \(\alpha\)Error de tipo I |
| \(H_o\)es falso | \(\beta\)Error de tipo II | \(1-\beta\)Poder |
Si una prueba de hipótesis tiene baja potencia, entonces sería difícil rechazarla\(H_o\), aunque\(H_o\) fuera falsa; la investigación sería una pérdida de tiempo y dinero. Sin embargo, analizar el poder es difícil ya que hay muchos valores del parámetro poblacional que sustentan\(H_a\). Por ejemplo, en el ejemplo de embotellado de salsa de soja, la Hipótesis Alternativa fue que la media no era de 16 onzas. Esto significa que la máquina podría estar llenando las botellas con una media de 16.0001 onzas, haciendo que Ha sea técnicamente cierto. Entonces, al analizar el poder y el error Tipo II, necesitamos elegir un valor para la media poblacional bajo la Hipótesis Alternativa (\(\mu_a\)) que sea “prácticamente diferente” de la media bajo la Hipótesis Null (\(\mu_o\)). Esta diferencia práctica se llama el tamaño del efecto.
Definición: Tamaño del efecto
Tamaño del efecto: La “diferencia práctica” entre\(\mu_{o}\) y\(\mu_a=\left|\mu_{o}-\mu_{a}\right|\)
donde
\(\mu_{o}\): El valor de la media poblacional bajo la Hipótesis Nula
\(\mu_{a}\): El valor de la media poblacional bajo la Hipótesis Alternativa
Supongamos que estamos realizando una prueba de una cola de la media poblacional:
\[H_o: \mu=\mu_{0} \qquad Ha: \mu>\mu_{0} \nonumber \]
Considera las dos gráficas que se muestran a continuación. La gráfica superior es la distribución de la media muestral bajo la Hipótesis Null, la cual fue cubierta en una sección anterior. El área a la derecha del valor crítico es la región de rechazo.
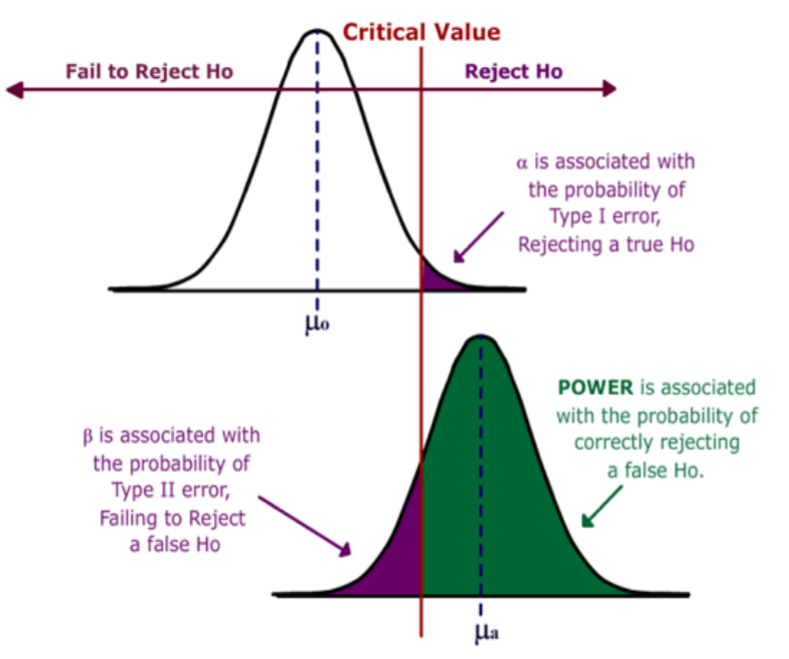
Ahora agregamos la gráfica inferior, que representa la distribución de la media muestral bajo la Hipótesis Alternativa para el valor específico\(\mu a\).
Ahora podemos medir el Poder de la prueba (el área en verde) y beta (el área en púrpura) en la gráfica inferior.
Existen varios métodos para aumentar el Poder, pero todos tienen compensaciones:
| Maneras de aumentar el poder | Intercambiar |
|---|---|
| Aumentar el tamaño de la muestra | Mayor costo o falta de disponibilidad de los datos |
| Aumentar el nivel de significancia (\(\alpha\)) | Más como Rechazar un verdadero\(H_o\) (error Tipo I) |
| Elija un\(\mu_{a}\) valor de\(\mu_{o}\) | El resultado puede ser menos significativo |
| Redefinir la población para disminuir la desviación estándar | El resultado puede ser demasiado limitado para tener valor |
| Conducta como una prueba de una cola en lugar de una prueba de dos colas | Puede producir un resultado sesgado |
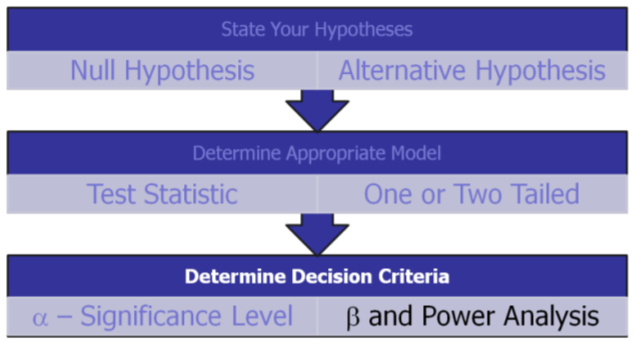
Ejemplo: Pastillas de freno de bus
Se afirma que las pastillas de freno de autobús duran en promedio al menos 60,000 millas y la compañía quiere probar esta afirmación. La compañía de autobuses considera que un valor “práctico” para fines de seguridad de autobuses es que las almohadillas duren al menos 58 mil millas. Si la desviación estándar es de 5,000 y el tamaño de la muestra es 50, encuentra la potencia de la prueba cuando la media es realmente de 58,000 millas. (Asumir\(\alpha = .05\))

Solución
Primero, encontrar el valor crítico de la prueba.
Rechazar\(H_o\) cuando\(Z < ‐1.645\)
A continuación, encontrar el valor de que corresponde al valor crítico.
\[\overline{X}=\mu_{o}+\dfrac{Z \sigma}{\sqrt{n}}=60000-(1.645)(5000) / \sqrt{50}=58837 \nonumber \]
\(H_o\)se rechaza cuando\(\overline{X}<58837\)
Finalmente, encuentra la probabilidad de rechazar\(H_o\) si Ha es verdadera.
\ [\ begin {alineado}
P (\ overline {X} <58837) &=P\ izquierda (Z<\ dfrac {\ izquierda (58837-\ mu_ {a}\ derecha)} {\ sigma/\ sqrt {n}}\ derecha)\\
&=P\ izquierda (Z<\ dfrac {(58837-58000)} {5000/\ sqrt {50}}\ derecha)\\
&=P (Z<1.18)\\
&=.8810
\ end {alineado} \ nonumber\]
Por lo tanto, esta prueba tiene 88% de potencia y\(\beta\) sería 12%
Valores de Cálculo de Potencia
Valores de entrada
\(\mu_{o}\)= 60.000 millas
\(\mu_{a}\)= 58,000 millas
\(\alpha\)= 0.05
\(n\)= 50
\(\sigma\)= 5000 millas
Valores calculados
Tamaño del efecto = 2000 millas
Valor Crítico = 58,837 millas
\(\beta\)= 0.1190 o aproximadamente 12%
Potencia = 0.8810 o aproximadamente 88%