15.2.2: Capítulo 3 Tareas

1. Se realizó una encuesta a 150 estudiantes del Colegio De Anza. A los alumnos se les preguntó cuántas horas trabajan fuera de la universidad. Los alumnos fueron entrevistados por la mañana entre las 8 AM y las 11 AM de un jueves. La media muestral para estos 150 estudiantes fue de 9.2 horas.
   1. ¿Qué es la Población?
   2. ¿Qué es la Muestra?
   3. ¿Las 9.2 horas representan una estadística o parámetro? Explique.
   4. ¿La media muestral de 9.2 es una estimación razonable del número medio de horas trabajadas para todos los estudiantes de De Anza? Explique cualquier posible sesgo.
2. Las parcelas de caja representan los resultados de tres exámenes para 40 alumnos de un curso de Matemáticas.

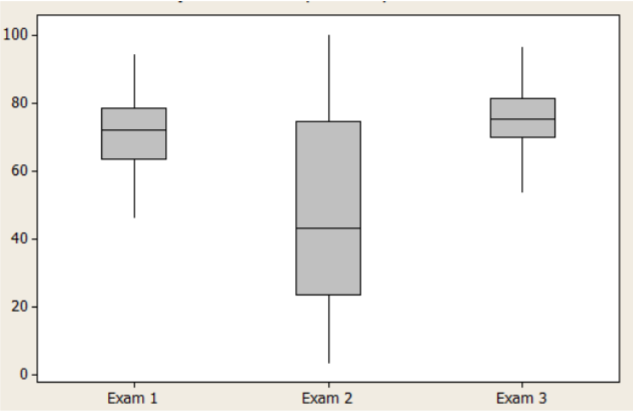
1. ¿Qué examen tiene la mediana más alta?
2. ¿Qué examen tiene la desviación estándar más alta?
3. Para el Examen 2, ¿cómo se compara la mediana con la media?
4. En sus propias palabras, compare los exámenes.

3. Examine el siguiente tiempo promedio diario de viaje (minutos) para residentes de dos ciudades.

1. Calcule e interprete la puntuación z para un viaje de 75 minutos para City A.
2. Calcule e interprete la puntuación z para un viaje de 75 minutos para City B.
3. ¿Para qué grupo sería más inusual un viaje de 75 ‐minutos? Explique.

4. A continuación se dan las calificaciones Nielsen del 10 de febrero de 2017 de 20 programas de televisión que se muestran en la televisión comercial, todos iniciando entre las 8 PM y las 10 PM:

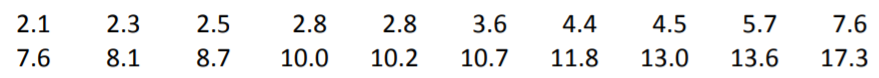
1. Obtener la media y mediana de la muestra. ¿Cree que los datos son simétricos, sesgados a la derecha o sesgados a la izquierda?
2. Determinar la varianza de la muestra y la desviación estándar.
3. Asumiendo que los datos tienen forma de campana, ¿entre qué dos números esperarías encontrar el 68% de los datos?

5. Los siguientes datos representan el tiempo de recuperación para 16 pacientes (dispuestos en una tabla para ayudarte).

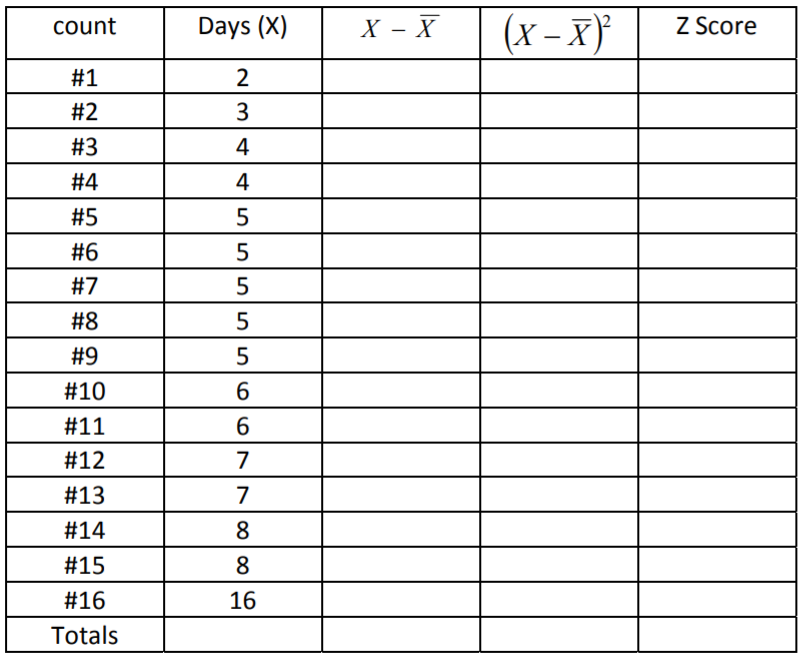
1. Calcular la media y mediana de la muestra
2. Utilice la tabla para calcular la varianza y desviación estándar.
3. Usa el rango de los datos para ver si la desviación estándar tiene sentido. (El rango debe estar entre 3 y 6 desviaciones estándar).
4. ¿Usando la regla empírica entre qué dos números debería esperar ver 68% de los datos? ¿95% de los datos? ¿99.7% de los datos?
5. Calcular la puntuación Z para la observación. ¿Crees que alguno de estos datos son valores atípicos?

6. Los siguientes datos representan las alturas (en pies) de 20 almendros en un huerto.

1. Construir una gráfica de caja de los datos.
2. ¿Crees que el árbol con la altura de 45 pies es un valor atípico? Usa el método de diagrama de caja para justificar tu respuesta.

7. En la tabla se muestra el siguiente tiempo promedio diario de viaje (en minutos) para residentes de 2 ciudades.

1. Encuentra los cuartiles y el rango intercuartílico para cada grupo.
2. Calcular el percentil 80 para cada grupo.
3. Construir parcelas de caja lado a lado y comparar los dos grupos

8. Clasificar los siguientes coeficientes de correlación de los más débiles a los más fuertes.

.343, ‐.318, .214, ‐.765, 0, .998, ‐.932, .445

9. Si estaba tratando de pensar en factores que afectan los costos de la atención médica:
   1. Elija una variable que crea que estaría correlacionada positivamente con los costos de atención médica.
   2. Elija una variable que crea que se correlacionaría negativamente con los costos de atención médica.
   3. Elija una variable que crea que no estaría correlacionada con los costos de atención médica.