Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

15.3.4: Capítulo 5 Laboratorio

Última actualización

31 oct 2022
Guardar como PDF
- 15.3.3: Capítulo 4 Laboratorio
- 15.3.5: Capítulo 6 Laboratorio

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Tabulación cruzada y tablas bidireccionales

Abra el archivo Minitab lab04.mpj desde el sitio web.

Aquí hay una descripción de los datos recopilados de las escuelas primarias en Michigan:

Género: (Niño, Niña)
Grado: 4, 5 o 6
Edad: Edad en años
Etnicidad: Blanca, Otra (Sí, ¡así fue la forma en que se reportó cuando se recolectaron estos datos!)
Ubicación: Rural, Suburbano, Urbano
Escuela: 1=Primaria Brentwood, 2=Brentwood Middle, 3=Ridge, 4=Arena, 5=Eureka, 6=Marrón, 7=Principal, 8=Portage, 9=Westdale Middle
Goles: Elección del estudiante en los objetivos personales: 1=Hacer buenas calificaciones, 2=Ser Popular, 3=Ser bueno en el Deporte
Grados: Rango de “hacer buenas calificaciones” (1=más importante para la popularidad, 4=menos importante)
Deportes: Rango de “ser bueno en los deportes” (1=más importante para la popularidad, 4=menos importante)
Looks: Rango de “ser guapo o bonito” (1=lo más importante para la popularidad, 4=menos importante)
Dinero: Rango de “tener mucho dinero” (1=más importante para la popularidad, 4=menos importante)

La tabulación cruzada es un método para tomar pares de variables categóricas y crear una tabla de dos vías. El comando se puede encontrar en la barra de menú STAT>TABLAS>CROSSTABULATION. Elija dos elementos de datos y verifique que desea contar, porcentajes de fila y porcentajes de columna. También puedes hacer un gráfico de barras agrupado>GRÁFICOS DE BARRAS>Agrupado. El ejemplo muestra una tabla cruzada de género con el nivel de grado:

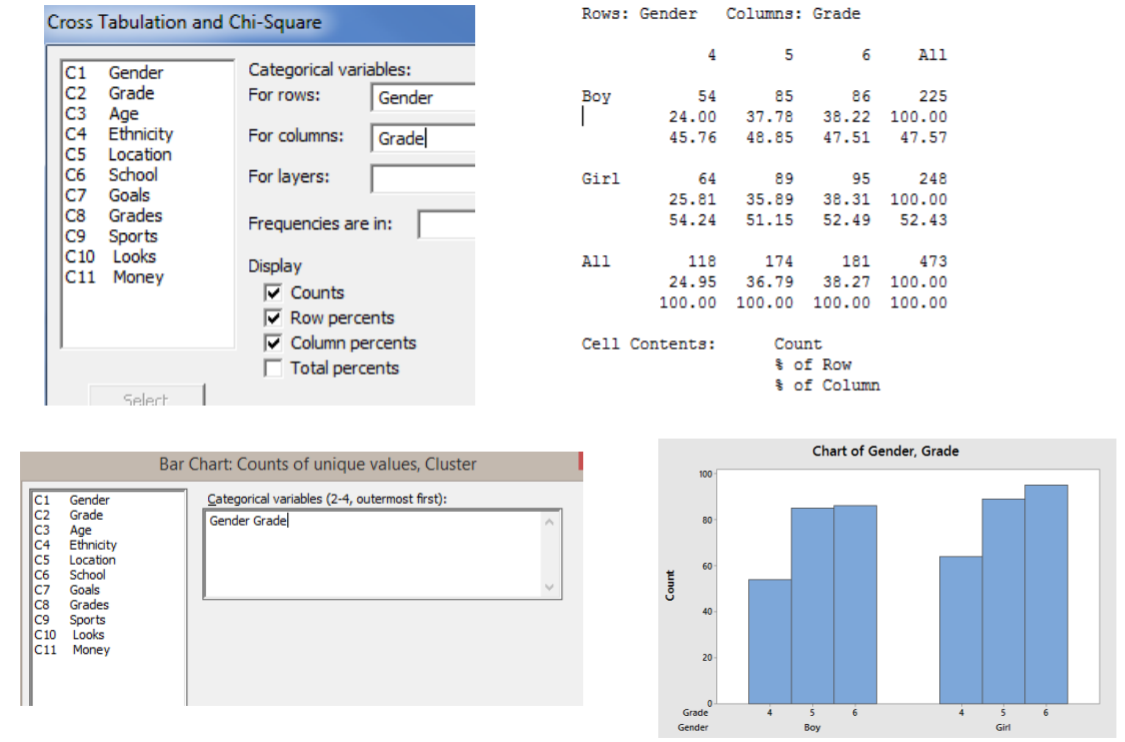
Cruza la tabulación de Género con Meta y crea una mesa de dos direcciones. Cree un gráfico de barras agrupado. Péguelos a los dos aquí.
1. ¿Cuál es la probabilidad de que un estudiante seleccionado al azar elija el deporte como el objetivo más importante? ¿Qué tipo de probabilidad es esta (Marginal, Conjunta o Condicional)?
2. ¿Cuál es la probabilidad de que un estudiante seleccionado al azar sea un niño? ¿Qué tipo de probabilidad es esta (Marginal, Conjunta o Condicional)?
3. ¿Cuál es la probabilidad de que un estudiante seleccionado al azar sea un niño y elija el deporte como objetivo más importante? ¿Qué tipo de probabilidad es esta (Marginal, Conjunta o Condicional)?
4. ¿Cuál es la probabilidad de que el niño seleccionado al azar elija el deporte como el objetivo más importante? ¿Qué tipo de probabilidad es esta (Marginal, Conjunta o Condicional)?
5. ¿Qué conclusiones puedes sacar sobre Género y Meta?
Cruza la tabla de ubicación con Goal y crea una mesa de dos vías. Cree gráficos circulares para Objetivo con una variable múltiple Ubicación en la misma gráfica. Pega los gráficos de tabulación cruzada y pastel aquí

¿Cuál es la probabilidad de que un estudiante seleccionado al azar elija el deporte como el objetivo más importante?
¿Cuál es la probabilidad de que un estudiante suburbano seleccionado al azar elija deportes?
¿Cuál es la probabilidad de que un estudiante rural seleccionado al azar elija deportes?
¿Cuál es la probabilidad de que un estudiante urbano seleccionado al azar elija deportes?
¿Qué conclusiones puedes sacar sobre Ubicación y Meta?

Tabla cruzada cualquiera de las dos variables de su elección y cree una tabla de dos vías. Cree un gráfico de barras agrupado. Péguelos a los dos aquí.
1. Calcula y explica cualquier probabilidad marginal de tu elección.
2. Calcula y explica cualquier probabilidad conjunta de tu elección.
3. Calcula y explica cualquier probabilidad condicional de tu elección.
4. ¿Qué conclusiones puedes sacar sobre estas dos variables?

Tabulación cruzada y tablas bidireccionales

Support Center

How can we help?