9.5: Distribución por muestreo de la media
- Page ID
- 152447
Objetivos de aprendizaje
- Indicar la media y varianza de la distribución muestral de la media
- Calcular el error estándar de la media
- Declarar el teorema del límite central
La distribución muestral de la media se definió en la sección de introducción de distribuciones de muestreo. En esta sección se revisan algunas propiedades importantes de la distribución muestral de la media introducida en las demostraciones de este capítulo.
Media de Muestreo
La media de la distribución muestral de la media es la media de la población de la que se muestrearon los puntajes. Por lo tanto, si una población tiene una media\(\mu\), entonces la media de la distribución muestral de la media es también\(\mu\). El símbolo\(\mu _M\) se utiliza para referirse a la media de la distribución muestral de la media. Por lo tanto, la fórmula para la media de la distribución muestral de la media puede escribirse como:
\[\mu _M = \mu\]
Varianza de muestreo
La varianza de la distribución muestral de la media se calcula de la siguiente manera:
\[ \sigma_M^2 = \dfrac{\sigma^2}{N}\]
Es decir, la varianza de la distribución muestral de la media es la varianza poblacional dividida por\(N\), el tamaño de la muestra (el número de puntuaciones utilizadas para calcular una media). Así, cuanto mayor es el tamaño de la muestra, menor es la varianza de la distribución muestral de la media.
Nota
(opcional) Esta expresión se puede derivar muy fácilmente de la ley de suma de varianza. Comencemos calculando la varianza de la distribución muestral de la suma de tres números muestreados de una población con varianza\(\sigma ^2\). The variance of the sum would be:
\[\sigma ^2 + \sigma ^2 + \sigma ^2\]
Por\(N\) numbers, the variance would be \(N\sigma ^2\). Since the mean is \(1/N\) times the sum, the variance of the sampling distribution of the mean would be \(1/N^2\) tiempos la varianza de la suma, que es igual\(\sigma ^2/N\).
El error estándar de la media es la desviación estándar de la distribución muestral de la media. Por lo tanto, es la raíz cuadrada de la varianza de la distribución muestral de la media y puede escribirse como:
\[ \sigma_M = \dfrac{\sigma}{\sqrt{N}}\]
El error estándar está representado por\(\sigma\) a porque es una desviación estándar. El subíndice (\(M\)) indica que el error estándar en cuestión es el error estándar de la media.
Teorema de Límite Central
Definición
El teorema del límite central establece que:
Dada una población con una media finita\(\mu\) y una varianza finita distinta de cero\(\sigma ^2\), la distribución muestral de la media se aproxima a una distribución normal con una media de\(\mu\) y una varianza de\(\sigma ^2/N\) as\(N\), the sample size, increases.
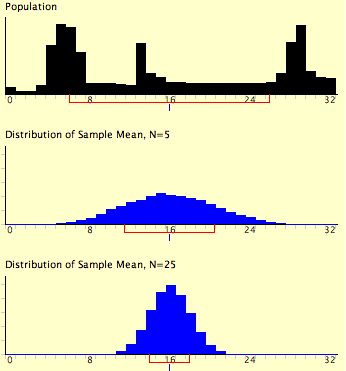
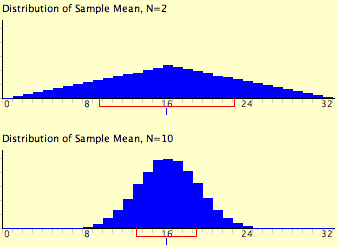
Las expresiones para la media y varianza de la distribución muestral de la media no son nuevas ni notables. Lo que es notable es que independientemente de la forma de la población parental, la distribución muestral de la media se acerca a una distribución normal a medida que\(N\) aumenta. Si has utilizado la “Demostración del Teorema de Límite Central”, ya lo has visto por ti mismo. Como recordatorio, la Figura\(\PageIndex{1}\) muestra los resultados de la simulación para\(N = 2\) y\(N = 10\). La población progenitora fue de distribución uniforme. Se puede ver que la distribución para\(N = 2\) está lejos de ser una distribución normal. No obstante, sí muestra que los puntajes son más densos en el medio que en las colas. Para\(N = 10\) la distribución es bastante cercana a una distribución normal. Observe que las medias de las dos distribuciones son las mismas, pero que el spread de la distribución para\(N = 10\) es menor.
La figura\(\PageIndex{2}\) muestra qué tan cerca la distribución muestral de la media se aproxima a una distribución normal incluso cuando la población parental es muy no normal. Si miras de cerca puedes ver que las distribuciones de muestreo sí tienen un ligero sesgo positivo. Cuanto mayor sea el tamaño de la muestra, más cerca estaría la distribución muestral de la media a una distribución normal.