9.6: Diferencia entre medias

Última actualización
Guardar como PDF

Page ID: 152457

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de aprendizaje

Indicar la media y varianza de la distribución muestral de la diferencia entre medias
Compute el error estándar de la diferencia entre medias
Compute la probabilidad de que una diferencia entre medias esté por encima de un valor especificado

Los análisis estadísticos se refieren muy a menudo a la diferencia entre medias. Un ejemplo típico es un experimento diseñado para comparar la media de un grupo control con la media de un grupo experimental. Las estadísticas inferenciales utilizadas en el análisis de este tipo de experimentos dependen de la distribución muestral de la diferencia entre medias.

La distribución muestral de la diferencia entre medias puede pensarse como la distribución que resultaría si repitiéramos los siguientes tres pasos una y otra vez:

\(n_1\)puntajes de muestra\(\text {Population 1}\) y\(n_2\) puntuaciones de\(\text {Population 2}\)
computar las medias de las dos muestras (\(M_1\)y\(M_2\))
computar la diferencia entre medias,\(M_1-M_2\)

La distribución de las diferencias entre medias es la distribución muestral de la diferencia entre medias.

Como cabría esperar, la media de la distribución muestral de la diferencia entre medias es:

\[\mu _{M_1-M_2}=\mu _1-\mu _2\]

que dice que la media de la distribución de las diferencias entre medias muestrales es igual a la diferencia entre medias poblacionales. Por ejemplo, decir que la puntuación media de la prueba de todos los\(12\) niños de un año en una población es\(34\) y la media de\(10\) -años es\(25\). Si se tomaran numerosas muestras de cada grupo etario y se calculara la diferencia de medias cada vez, la media de estas numerosas diferencias entre las medias de la muestra sería\(34-25=9\).

De la ley de suma de varianza, sabemos que:

\[\sigma _{M_1-M_2}^{2}=\sigma _{M_1}^{2}+\sigma _{M_2}^{2}\]

que dice que la varianza de la distribución muestral de la diferencia entre medias es igual a la varianza de la distribución muestral de la media para\(\text {Population 1}\) más la varianza de la distribución muestral de la media para\(\text {Population 2}\). Recordemos la fórmula para la varianza de la distribución muestral de la media:

\[\sigma _{M}^{2}=\frac{\sigma ^2}{N}\]

Dado que tenemos dos poblaciones y dos tamaños de muestras, necesitamos distinguir entre las dos varianzas y tamaños de muestra. Hacemos esto mediante el uso de los subíndices\(1\) y\(2\). Usando esta convención, podemos escribir la fórmula para la varianza de la distribución muestral de la diferencia entre medias como:

\[\sigma _{M_1-M_2}^{2}=\frac{\sigma _1^2}{n_1}+\frac{\sigma _2^2}{n_2}\]

Dado que el error estándar de una distribución de muestreo es la desviación estándar de la distribución de muestreo, el error estándar de la diferencia entre medias es:

\[\sigma _{M_1-M_2}=\sqrt{\frac{\sigma _1^2}{n_1}+\frac{\sigma _2^2}{n_2}}\]

Sólo para revisar la notación, el símbolo de la izquierda contiene un sigma (\(\sigma\)), lo que significa que es una desviación estándar. Los subíndices\(M_1-M_2\) indican que es la desviación estándar de la distribución muestral de\(M_1-M_2\).

Ahora veamos una aplicación de esta fórmula.

Ejemplo\(\PageIndex{1}\)

Supongamos que hay dos especies de seres verdes en Marte. La altura media de\(\text{Species 1}\) es\(32\) mientras que la altura media de\(\text{Species 2}\) es\(22\). Las varianzas de las dos especies son\(60\) y\(70\), respectivamente y las alturas de ambas especies se distribuyen normalmente. Muestrea aleatoriamente\(10\) miembros de\(\text{Species 1}\) y\(14\) miembros de\(\text{Species 2}\). ¿Cuál es la probabilidad de que la media de los\(10\) miembros de\(\text{Species 1}\) supere la media de los\(14\) miembros de\(\text{Species 2}\) por\(5\) o más? Sin hacer ningún cálculo, probablemente sepas que la probabilidad es bastante alta ya que la diferencia en medias poblacionales lo es\(10\). Pero, ¿cuál es exactamente la probabilidad?

Solución

Primero, determinemos la distribución muestral de la diferencia entre medias. Usando las fórmulas anteriores, la media es

\[\mu _{M_1-M_2}=32-22=10\]

El error estándar es:

\[\sigma _{M_1-M_2}=\sqrt{\frac{60}{10}+\frac{70}{14}}=3.317\]

La distribución muestral se muestra en la Figura\(\PageIndex{1}\). Observe que normalmente se distribuye con una media de\(10\) y una desviación estándar de\(3.317\). El área de arriba\(5\) es de color azul sombreado.

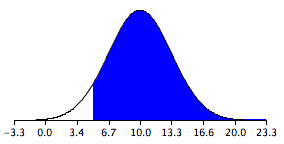
muestreo distribution.gif — Figura\(\PageIndex{1}\): La distribución muestral de la diferencia entre medias

El último paso es determinar el área que está sombreada en azul. Usando ya sea una\(Z\) tabla o la calculadora normal, se puede determinar que el área sea\(0.934\). Así la probabilidad de que la media de la muestra de\(\text{Species 1}\) supere la media de la muestra de\(\text{Species 2}\) por\(5\) o más es\(0.934\).

Como se muestra a continuación, la fórmula para el error estándar de la diferencia entre medias es mucho más simple si los tamaños de muestra y las varianzas de la población son iguales. Cuando las varianzas y tamaños de las muestras son los mismos, no hay necesidad de utilizar los subíndices\(1\) y\(2\) diferenciar estos términos.

\[\sigma _{M_1-M_2}=\sqrt{\frac{\sigma _1^2}{n_1}+\frac{\sigma _2^2}{n_2}}=\sqrt{\frac{\sigma ^2}{n}+\frac{\sigma ^2}{n}}=\sqrt{\frac{2\sigma ^2}{n}}\]

Esta versión simplificada de la fórmula se puede utilizar para el siguiente problema.

Ejemplo\(\PageIndex{2}\)

La estatura media\(15\) de los niños de un año (en cm) es\(175\) y la varianza es\(64\). Para las niñas, la media es\(165\) y la varianza es\(64\). Si se muestrearan ocho niños y ocho niñas, ¿cuál es la probabilidad de que la estatura media de la muestra de niñas sea mayor que la estatura media de la muestra de niños? En otras palabras, ¿cuál es la probabilidad de que la estatura media de las niñas menos la estatura media de los niños sea mayor que\(0\)?

Solución

Como antes, el problema puede resolverse en términos de la distribución muestral de la diferencia entre medias (niñas - niños). La media de la distribución es 165 - 175 = -10. La desviación estándar de la distribución es:

\[\sigma _{M_1-M_2}=\sqrt{\frac{2\sigma ^2}{n}}=\sqrt{\frac{(2)(64)}{8}}=4\]

En la Figura se muestra una gráfica de la distribución\(\PageIndex{2}\). Es claro que es poco probable que la estatura media para las niñas sea mayor que la estatura media para los niños ya que en la población los chicos son bastante más altos. Sin embargo, no es inconcebible que la media de las niñas pueda ser mayor que la media de los chicos.

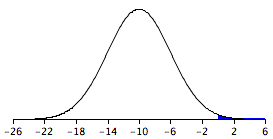
boy_girl example.gif — Figura\(\PageIndex{2}\): Distribución de muestreo S de la diferencia entre alturas medias

Una diferencia entre medias de 0 o superiores es una diferencia de desviaciones\(10/4 = 2.5\) estándar por encima de la media de\(-10\). La probabilidad de una puntuación\(2.5\) o más desviaciones estándar por encima de la media es\(0.0062\).