9.E: Distribuciones de Muestreo (Ejercicios)
- Page ID
- 152443
Es posible que desee utilizar la calculadora “r a z'” y el applet “Calcular área para una X determinada” para algunos de estos ejercicios.
Preguntas Generales
Q1
Una población tiene una media de\(50\) y una desviación estándar de\(6\).
- ¿Cuáles son la media y la desviación estándar de la distribución muestral de la media para\(N = 16\)?
- ¿Cuáles son la media y la desviación estándar de la distribución muestral de la media para\(N = 20\)? (sección pertinente)
Q2
Dada una prueba que normalmente se distribuye con una media de\(100\) y una desviación estándar de\(12\), encontrar:
- la probabilidad de que una sola puntuación sorteada al azar sea mayor que\(110\) (sección relevante)
- la probabilidad de que una muestra de\(25\) puntuaciones tenga una media mayor que\(105\) (sección relevante)
- la probabilidad de que una muestra de\(64\) puntuaciones tenga una media mayor que\(105\) (sección relevante)
- la probabilidad de que la media de una muestra de\(16\) puntuaciones sea menor\(95\) o mayor que\(105\) (sección relevante)
Q3
¿Qué término se refiere a la desviación estándar de la distribución muestral? (sección pertinente)
Q4
- Si el error estándar de la media es\(10\) para\(N = 12\), ¿para qué sirve el error estándar de la media\(N = 22\)?
- Si el error estándar de la media es\(50\) para\(N = 25\), ¿para qué sirve\(N = 64\)? (sección pertinente)
Q5
Se desarrolla un cuestionario para evaluar las actitudes de mujeres y hombres hacia el uso de animales en la investigación. Una pregunta pregunta si la investigación animal es incorrecta y se responde en una\(7\) escala de puntos. Supongamos que en la población, la media para las mujeres es\(5\), la media para los hombres es\(4\), y la desviación estándar para ambos grupos lo es\(1.5\). Supongamos que las puntuaciones se distribuyen normalmente. Si\(12\) mujeres y\(12\) hombres son seleccionados al azar, ¿cuál es la probabilidad de que la media de las mujeres sea más que\(1.5\) puntos mayor que la media de los hombres? (sección pertinente)
Q6
Si la correlación entre el logro de lectura y el logro matemático en la población de quinto grado fuera\(0.60\), ¿cuál sería la probabilidad de que en una muestra de\(28\) estudiantes, el coeficiente de correlación muestral sea mayor que\(0.65\)? (sección pertinente)
Q7
Si\(N = 15\) se toman numerosas muestras de una distribución uniforme y se dibuja una distribución de frecuencia relativa de las medias, ¿cuál sería la forma de la distribución de frecuencias? (sección relevante y sección relevante)
Q8
Una distribución normal tiene una media de\(20\) y una desviación estándar de\(10\). Dos puntuaciones se muestrean aleatoriamente de la distribución y la segunda puntuación se resta de la primera. ¿Cuál es la probabilidad de que la puntuación de diferencia sea mayor que\(5\)? Pista: Lea la sección Ley de Suma de Varianza del Capítulo 3. (sección relevante y sección relevante)
Q9
¿Cuál es la forma de la distribución muestral\(r\)? ¿De qué manera la forma depende del tamaño de la correlación poblacional? (sección pertinente)
Q10
Si muestrea un número de una distribución normal estándar, ¿cuál es la probabilidad de que sea\(0.5\)? (sección relevante y sección relevante)
Q11
Una variable se distribuye normalmente con una media de\(120\) y una desviación estándar de\(5\). Cuatro puntuaciones se muestrean aleatoriamente. ¿Cuál es la probabilidad de que la media de las cuatro puntuaciones esté por encima\(127\)? (sección pertinente)
Q12
La correlación entre la autoestima y la extraversión es\(0.30\). Se toma una\(84\) muestra de.
- ¿Cuál es la probabilidad de que la correlación sea menor que\(0.10\)?
- ¿Cuál es la probabilidad de que la correlación sea mayor que\(0.25\)? (sección pertinente)
Q13
El promedio de promedio para los estudiantes en\(\text{School A}\) es\(3.0\); el promedio de promedio para los estudiantes en\(\text{School B}\) es\(2.8\). La desviación estándar en ambas escuelas es\(0.25\). Normalmente se distribuyen los GPA de ambas escuelas. Si\(9\) los alumnos son muestreados aleatoriamente de cada escuela, cuál es la probabilidad de que:
- la media de la muestra para\(\text{School A}\) superará la\(\text{School A}\) de en\(0.5\) o más? (sección pertinente)
- la media de la muestra para\(\text{School B}\) será mayor que la media de la muestra para\(\text{School A}\)? (sección pertinente)
Q14
En una ciudad,\(70\%\) de la gente prefiere\(\text{Candidate A}\). Supongamos que se muestrearon\(30\) personas de esta ciudad.
- ¿Cuál es la media de la distribución muestral de\(p\)?
- ¿Cuál es el error estándar de\(p\)?
- ¿Cuál es la probabilidad de que\(80\%\) o más de esta muestra prefiera\(\text{Candidate A}\)?
- ¿Cuál es la probabilidad de que\(45\%\) o más de esta muestra prefiera algún otro candidato? (sección pertinente)
Q15
A la hora de resolver problemas donde se necesita la distribución de muestreo\(r\), ¿cuál es el motivo de la conversión de\(r\) a\(z'\)? (sección pertinente)
Q16
En la población, la puntuación media del SAT es\(1000\). ¿Sería más probable (o igualmente probable) obtener una media de muestra de\(1200\) si muestreó aleatoriamente a\(10\) estudiantes o si muestreó aleatoriamente a\(30\) estudiantes? Explique. (sección relevante y sección relevante)
Q17
Verdadero/falso: El error estándar de la media es\(N = 20\) menor cuando que cuando\(N = 10\). (sección pertinente)
Q18
Verdadero/falso: La distribución muestral de\(r =0.8\) se vuelve normal a medida que\(N\) aumenta. (sección pertinente)
Q19
Verdadero/falso: Usted elige a\(20\) los estudiantes de la población y calcula la media de sus puntajes en las pruebas. Se repiten los\(100\) tiempos de este proceso y se traza la distribución de los medios. En este caso, el tamaño de la muestra es\(100\). (sección relevante y sección relevante)
Q20
Verdadero/falso: En tu escuela,\(40\%\) de los alumnos ven televisión por la noche. Al azar preguntas a\(5\) los estudiantes todos los días si ven televisión por la noche. Todos los días, encontrarías eso\(2\) del\(5\) do ver televisión por la noche. (sección relevante y sección relevante)
Q21
Verdadero/falso: La mediana tiene una distribución de muestreo. (sección pertinente)
Q22
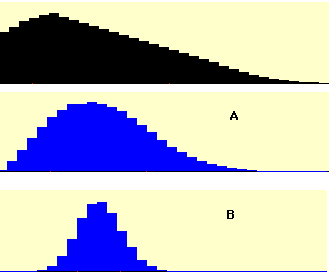
Verdadero/falso: Consulte la siguiente figura. La distribución poblacional se muestra en negro, y su distribución muestral correspondiente de la media para\(N = 10\) se etiqueta\(A\) "" (sección relevante y sección relevante)
Preguntas de casos prácticos
Las siguientes preguntas utilizan datos del estudio de caso Angry Moods (AM).
Q23
- ¿Cuántos hombres fueron muestreados?
- ¿Cuántas mujeres fueron muestreadas?
Q24
¿Cuál es la diferencia de medias entre hombres y mujeres en los puntajes de Anger-Out?
Q25
Supongamos que en la población, el puntaje de Anger-Out para los hombres es dos puntos mayor que para las mujeres. Las variaciones poblacionales para hombres y mujeres son ambas\(20\). Supongamos que los puntajes de Anger-Out para ambos géneros se distribuyen normalmente. Dada esta información sobre los parámetros poblacionales:
- ¿Cuál es la media de la distribución muestral de la diferencia entre medias? (sección pertinente)
- ¿Cuál es el error estándar de la diferencia entre medias? (sección pertinente)
- ¿Cuál es la probabilidad de que hubieras obtenido esta diferencia media (ver #24) o menos en tu muestra? (sección pertinente)
Las siguientes preguntas utilizan datos del estudio de caso Animal Research (AR).
Q26
¿Cuántas personas fueron muestreadas para dar sus opiniones sobre la investigación animal?
Q27
(AR #11) ¿Cuál es la correlación en esta muestra entre la creencia de que la investigación animal es incorrecta y la creencia de que la investigación animal es necesaria? (Ch. 4.E)
Q28
Supongamos que la correlación entre la creencia de que la investigación animal es incorrecta y la creencia de que la investigación animal es necesaria está\(-0.68\) en la población.
- Convertir\(-0.68\) a\(z'\). (sección pertinente)
- Encuentra el error estándar de esta distribución de muestreo. (sección pertinente)
- En una nueva muestra, ¿cuál es la probabilidad de que obtengas la correlación encontrada en la muestra original (ver #27) o una correlación menor (más cercana a\(-1\))? (sección pertinente)
Respuestas Seleccionadas
S1
- Media =\(50\), DE =\(1.5\)
S2
- \(0.019\)
S4
- \(7.39\)
S11
\(0.0026\)
S12
- \(0.690\)
S13
- \(0.0055\)
S 14
- \(0.116\)
S23
- \(30\)
S25
- \(2\)
S28
- \(0.603\)


