15.5: Multi-Factor Entre Sujetos
- Page ID
- 152297
Objetivos de aprendizaje
- Definir efecto principal, efecto simple, interacción y media marginal
- Indicar la relación entre los efectos simples y la interacción
- Calcular la fuente de variación y df para cada efecto en un diseño factorial
- Trazar las medias para una interacción
- Definir interacción de tres vías
Conceptos básicos y términos
En el estudio de caso “Sesgo Against Associates of the Obese”, los investigadores estaban interesados en saber si el peso de un compañero de un aspirante a un empleo afectaría los juicios de las calificaciones de un aspirante masculino para un empleo. Se investigaron dos variables independientes:
- si el acompañante era obeso o de peso típico y
- si la compañera era novia o simplemente un conocido.
Un enfoque podría haber sido realizar dos estudios separados, uno con cada variable independiente. Sin embargo, es más eficiente realizar un estudio que incluya ambas variables independientes. Además, hay una ventaja mucho mayor que la eficiencia para incluir dos variables en un mismo estudio: permite una prueba de la interacción entre las variables. Hay una interacción cuando el efecto de una variable difiere dependiendo del nivel de una segunda variable. Por ejemplo, es posible que el efecto de tener un compañero obeso difiera dependiendo de la relación con el compañero. Quizás haya más prejuicio contra una persona con una compañera obesa si la compañera es novia que si solo es una conocida. De ser así, habría una interacción entre el factor obesidad y el factor de relación.
Hay tres efectos de interés en este experimento:
- Peso: ¿Los aspirantes se juzgan de manera diferente dependiendo del peso de su acompañante?
- Relación: ¿Los aspirantes se juzgan de manera diferente dependiendo de su relación con su acompañante?
- Peso x Relación Interacción: ¿El efecto del peso difiere dependiendo de la relación con el compañero?
Los dos primeros efectos (Peso y Relación) son ambos efectos principales. Un efecto principal de una variable independiente es el efecto de la variable promediando sobre los niveles de la otra (s) variable (s). Es conveniente hablar de efectos principales en términos de medios marginales. Una media marginal para un nivel de una variable es la media de las medias de todos los niveles de la otra variable. Por ejemplo, la media marginal para el nivel “Obeso” es la media de “Novia obesa” y “Conocido obeso”. \(\PageIndex{1}\)El cuadro muestra que esta media marginal es igual a la media de\(5.65\) y\(6.15\), que es\(5.90\). De igual manera, la media marginal para el nivel “Típico” es la media de\(6.19\) y\(6.59\), que es\(6.39\). El efecto principal de Peso se basa en una comparación de estas dos medias marginales. De igual manera, los medios marginales para “Novia” y “Conocido” son\(5.92\) y\(6.37\).
| Peso acompañante | ||||
|---|---|---|---|---|
| Obesos | Típico | Media Marginal | ||
| Relación | Novia | 5.65 | 6.19 | 5.92 |
| Conocido | 6.15 | 6.59 | 6.37 | |
| Media Marginal | 5.90 | 6.39 | ||
En contraste con un efecto principal, que es el efecto de una variable promediada a través de niveles de otra variable, el efecto simple de una variable es el efecto de la variable en un solo nivel de otra variable. El simple efecto de Peso a nivel de “Novia” es la diferencia entre las condiciones “Novia Típica” y las “Novia Obesa”. La diferencia es\(6.19-5.65 = 0.54\). De igual manera, el efecto simple del Peso a nivel de “Conocido” es la diferencia entre las condiciones “Conocido Típico” y “Conocido Obeso”. La diferencia es\(6.59-6.15 = 0.44\).
Recordemos que existe una interacción cuando el efecto de una variable difiere dependiendo del nivel de otra variable. Esto equivale a decir que hay una interacción cuando los efectos simples difieren. En este ejemplo, los efectos simples del peso son\(0.54\) y\(0.44\). Como se muestra a continuación, estos efectos simples no son significativamente diferentes.
Pruebas de significación
Las preguntas importantes no son si hay efectos principales e interacciones en los datos de la muestra. En cambio, lo importante es lo que los datos de la muestra permiten concluir sobre la población. Aquí es donde entra en juego el Análisis de Varianza. ANOVA prueba los principales efectos e interacciones para determinar la significación. En la Tabla se muestra una Tabla de Resumen de ANOVA para estos datos\(\PageIndex{2}\).
| Fuente | df | SSQ | MS | F | p |
|---|---|---|---|---|---|
| Peso | 1 | 10.4673 | 10.4673 | 6.214 | 0.0136 |
| Relación | 1 | 8.8144 | 8.8144 | 5.233 | 0.0234 |
| Ancho x Alto | 1 | 0.1038 | 0.1038 | 0.062 | 0.8043 |
| Error | 172 | 289.7132 | 1.6844 | ||
| Total | 175 | 310.1818 |
Considera primero el efecto de “Peso”. Los grados de libertad (\(df\)) para “Peso” es\(1\). Los grados de libertad para un efecto principal siempre son iguales al número de niveles de la variable menos uno. Dado que existen dos niveles de la variable “Peso” (típica y obesa), la\(df\) es\(2 - 1 = 1\). Nos saltamos el cálculo de la suma de cuadrados (\(SSQ\)) no porque sea difícil, sino porque es mucho más fácil confiar en programas de computadora para calcularlo. El cuadrado medio (\(MS\)) es la suma de cuadrados dividida por el\(df\). La\(F\) relación se calcula dividiendo el\(MS\) para el efecto por el\(MS\) para el error (\(MSE\)). Por el efecto de “Peso”,\(F = 10.4673/1.6844 = 6.214\). La última columna,\(p\), es la probabilidad de obtener un\(F\) de\(6.214\) o mayor dado que no hay efecto de peso en la población. El\(p\) valor es\(0.0136\) y por lo tanto se rechaza la hipótesis nula de no efecto principal de “Peso”. La conclusión es que estar acompañado por un compañero obeso disminuye los juicios de calificaciones.
El efecto “Relación” se interpreta de la misma manera. La conclusión es que estar acompañado por una novia lleva a calificaciones más bajas que estar acompañado por un conocido.
El\(df\) para una interacción es el producto\(df's\) de las variables en la interacción. Para la interacción “Peso x Relación” (\(W \times R\)), el\(df = 1\) ya que tanto Peso como Relación tienen uno\(df: 1 \times 1 = 1\). El\(p\) valor para la interacción es\(0.8043\), que es la probabilidad de obtener una interacción tan grande o mayor que la obtenida en el experimento si no hubo interacción en la población. Por lo tanto, estos datos no proporcionan evidencia de una interacción. Siempre tenga en cuenta que la falta de pruebas para un efecto no justifica la conclusión de que no hay efecto. En otras palabras, no aceptas la hipótesis nula solo porque no la rechazas.
Para “Error”, los grados de libertad son iguales al número total de observaciones menos el número total de grupos. Los tamaños de muestra de las cuatro condiciones en este experimento se muestran en la Tabla\(\PageIndex{3}\). El número total de observaciones es\(40 + 42 + 40 + 54 = 176\). Dado que hay cuatro grupos,\(dfe = 176 - 4 = 172\).
| Peso acompañante | |||
|---|---|---|---|
| Obesos | Típico | ||
| Relación | Novia | 40 | 42 |
| Conocido | 40 | 54 | |
La fila final en la Tabla de Resumen de ANOVA es “Total”. El total de grados de libertad es igual a la suma de todos los grados de libertad. También es igual a la\(\textit{number of observations minus 1}\), o\(176 - 1 = 175\). Cuando hay tamaños de muestra iguales, la suma de cuadrados totales será igual a la suma de todas las demás sumas de cuadrados. Sin embargo, cuando hay tamaños de muestra desiguales, como los hay aquí, esto generalmente no será cierto. Las razones de esto son complejas y se discuten en la sección Tamaños de Muestra Desiguales.
Medios de trazado
Aunque la gráfica mostrada en la Figura\(\PageIndex{1}\) ilustra los efectos principales así como la interacción (o falta de interacción), se denomina gráfica de interacción. Es importante considerar cuidadosamente los componentes de esta parcela. En primer lugar, la variable dependiente está en el\(Y\) eje -eje. En segundo lugar, una de las variables independientes está en el\(X\) eje -eje. En este caso, es la variable “Peso”. Finalmente, se dibuja una línea separada para cada nivel de la otra variable independiente. Es mejor etiquetar las líneas justo en la gráfica, como se muestra aquí, que con una leyenda.
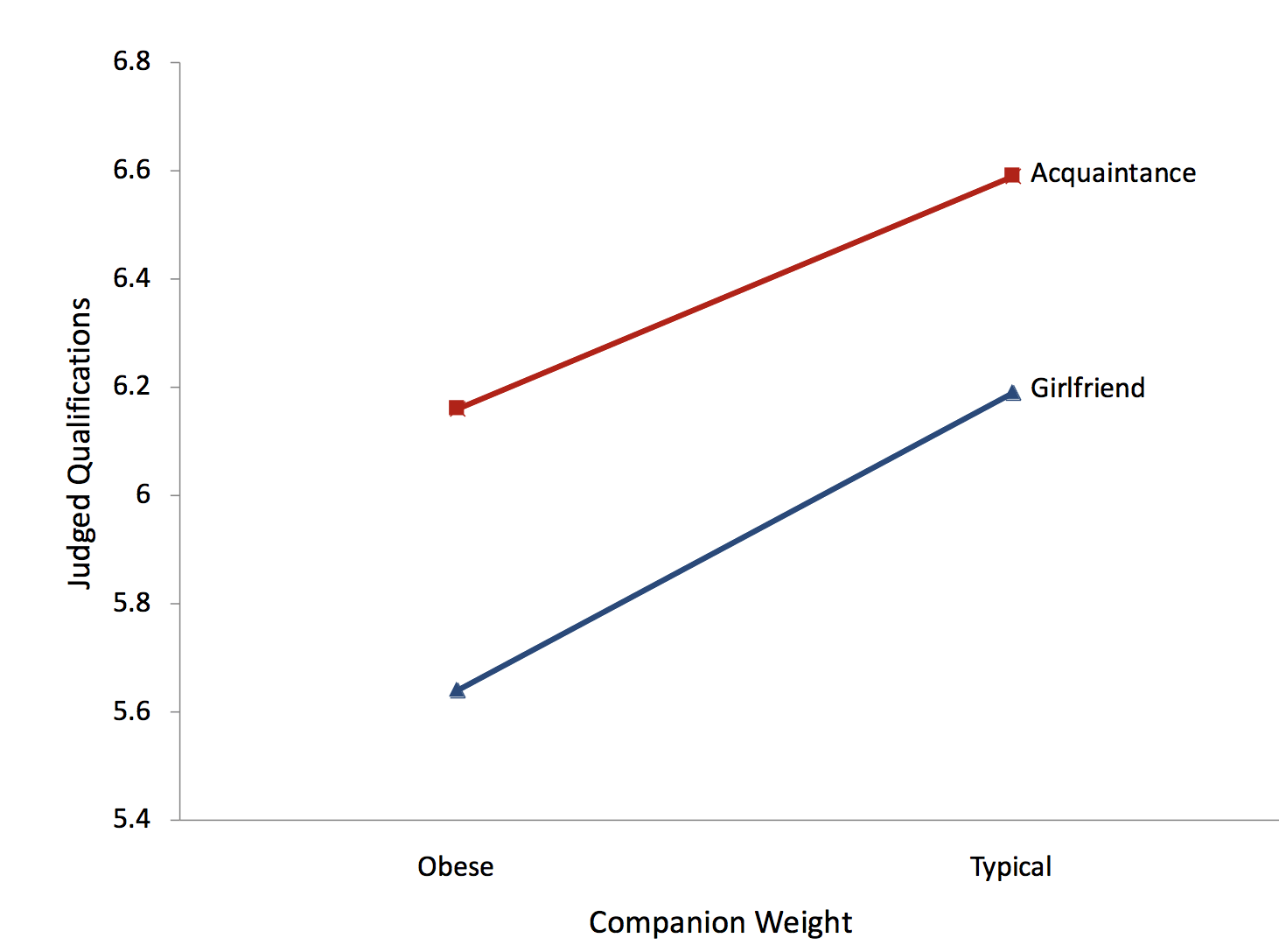
Si tienes tres o más niveles en el\(X\) eje, no debes usar líneas a menos que haya algún orden numérico a los niveles. Si tu variable en el\(X\) eje -es una variable cualitativa, puedes usar una gráfica como la de la Figura\(\PageIndex{2}\). No obstante, como se discutió en la sección sobre gráficos de barras, sería mejor reemplazar cada barra por una gráfica de caja.
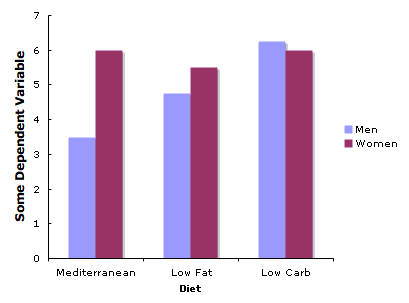
La figura\(\PageIndex{3}\) muestra una gráfica de este tipo. Observe cómo contiene información sobre las medianas, cuantiles y mínimos y máximos no contenidos en la Figura\(\PageIndex{2}\). Lo más importante es que se tiene una idea de cuánto se superponen las distribuciones de Figura\(\PageIndex{3}\) que no obtiene de Figura\(\PageIndex{2}\).
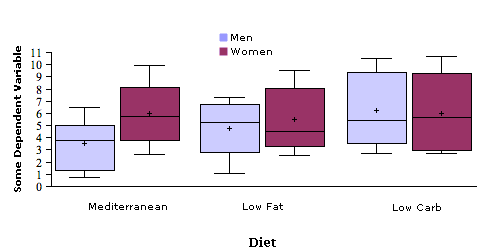
Los gráficos de líneas son una buena opción cuando hay más de dos niveles de una variable numérica. La figura\(\PageIndex{4}\) muestra un ejemplo. Un gráfico de líneas tiene la ventaja de mostrar claramente el patrón de interacción. Su desventaja es que no transmite la información distributiva contenida en las parcelas de caja.
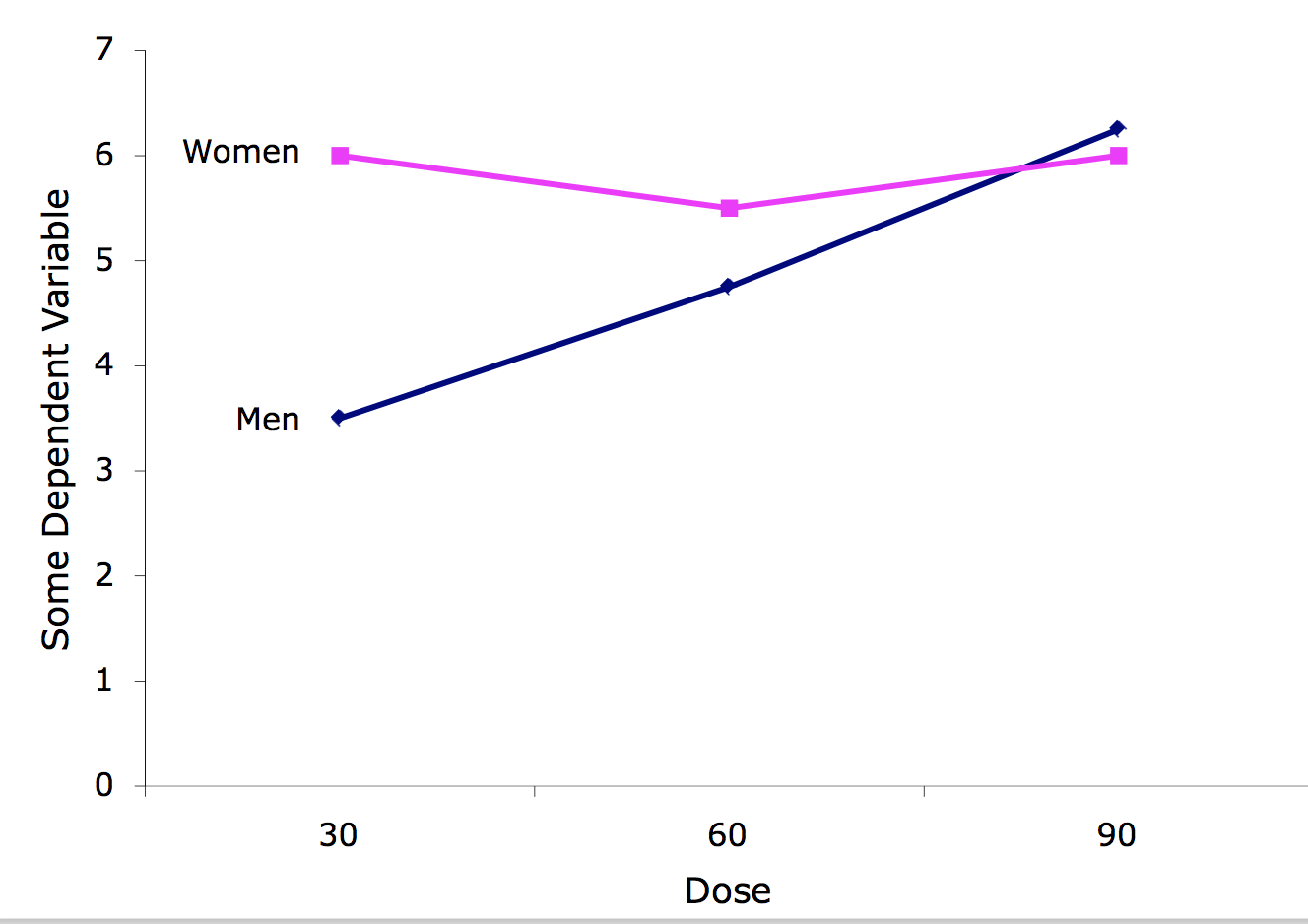
Un Ejemplo con Interacción
El siguiente ejemplo se presentó en la sección de comparaciones específicas entre medias. También es relevante aquí.
En este ejemplo se utilizan los datos inventados de un experimento hipotético que se muestra en la Tabla\(\PageIndex{4}\). Se seleccionaron 12 sujetos de una población de sujetos de alta autoestima y se seleccionó un\(12\) sujeto adicional de una población de sujetos de baja autoestima. Luego los sujetos se desempeñaron en una tarea y (independientemente de lo bien que realmente lo hicieran) a la mitad de cada categoría de estima se les dijo que tenían éxito y a la otra mitad se les dijo que fallaron. Por lo tanto, hubo seis sujetos en cada una de las cuatro combinaciones estima/resultado y\(24\) sujetos en todas.
Después de la tarea, se pidió a los sujetos que calificaran (en una escala de\(10\) puntos) cuánto de su resultado (éxito o fracaso) se atribuían a sí mismos en lugar de deberse a la naturaleza de la tarea.
| Estima | |||
|---|---|---|---|
| Alto | Bajo | ||
| Resultado | Éxito | 7 | 6 |
| 8 | 5 | ||
| 7 | 7 | ||
| 8 | 4 | ||
| 9 | 5 | ||
| 5 | 6 | ||
| Fracaso | 4 | 9 | |
| 6 | 8 | ||
| 5 | 9 | ||
| 4 | 8 | ||
| 7 | 7 | ||
| 3 | 6 | ||
El Cuadro Resumen de ANOVA para estos datos se muestra en la Tabla\(\PageIndex{5}\).
| Fuente | df | SSQ | MS | F | p |
|---|---|---|---|---|---|
| Resultado | 1 | 0.0417 | 0.0417 | 0.0256 | 0.8744 |
| Estima | 1 | 2.0417 | 2.0417 | 1.2564 | 0.2756 |
| O x E | 1 | 35.0417 | 35.0417 | 21.5641 | 0.0002 |
| Error | 20 | 32.5000 | 1.6250 | ||
| Total | 23 | 69.6250 |
Como puede ver, el único efecto significativo es la interacción\(Outcome \times Esteem\) (\(O \times E\)). La forma de la interacción se puede ver en la Figura\(\PageIndex{5}\).
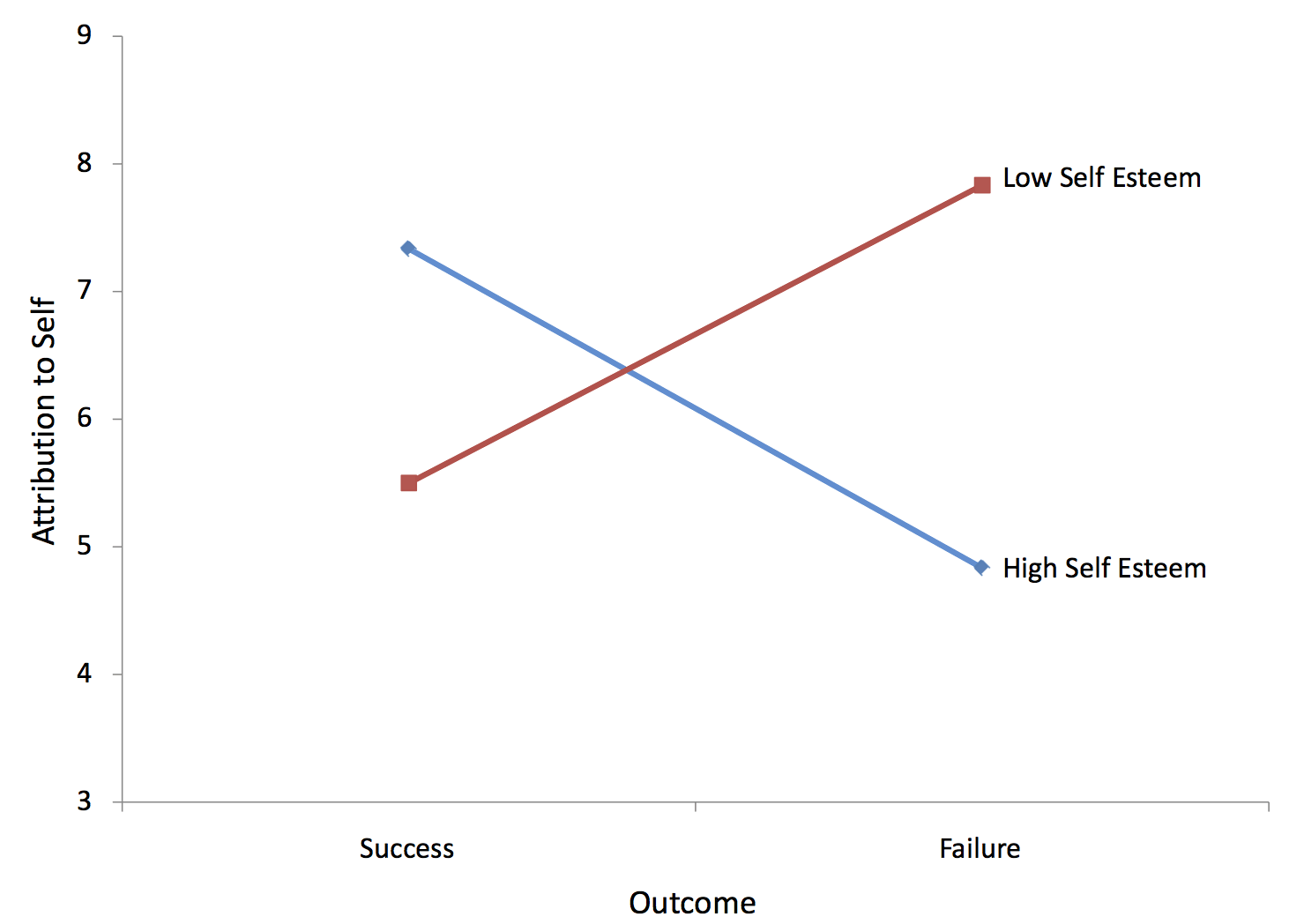
Claramente el efecto de “Resultado” es diferente para los dos niveles de “Estima”: Para sujetos altos en autoestima, el fracaso llevó a menos atribución a uno mismo que el éxito. Por el contrario, para los sujetos bajos en autoestima, el fracaso llevó a una mayor atribución a uno mismo que el éxito. Observe que las dos líneas de la gráfica no son paralelas. Las líneas no paralelas indican interacción. La prueba de significancia para la interacción determina si se justifica concluir que las líneas en la población no son paralelas. Las líneas no tienen que cruzar para que haya una interacción.
Diseños de tres factores
Los diseños de tres factores se analizan de la misma manera que los diseños de dos factores. \(\PageIndex{6}\)La tabla muestra el análisis de un estudio descrito por Franklin y Cooley que investiga tres factores sobre la resistencia de los ventiladores industriales:
- Forma de agujero (hexagonal o redondo)
- Método de Ensamblaje (Estacado o Hilado), y
- Superficie del Barril (Moleteado o Liso).
La variable dependiente, Fractura Torque, se midió en pie-libras. Hubo ocho observaciones en cada una de las ocho combinaciones de los tres factores.
Como puede ver en Table\(\PageIndex{6}\), hay tres efectos principales, tres interacciones bidireccionales y una interacción de tres vías. Los grados de libertad para los efectos principales son, como en un diseño de dos factores, igual al número de niveles del factor menos uno. Como todos los factores aquí tienen dos niveles, todos los efectos principales tienen un grado de libertad. Los grados de libertad de interacción siempre son iguales al producto de los grados de libertad de las partes componentes. Esto es válido para la interacción de tres factores, así como para las interacciones de dos factores. Los grados de libertad de error son iguales al número de observaciones (\(64\)) menos el número de grupos (\(8\)) e iguales\(56\).
| Fuente | df | SSQ | MS | F | p |
|---|---|---|---|---|---|
| Agujero | 1 | 8258.27 | 8258.27 | 266.68 | <0.0001 |
| Ensamblaje | 1 | 13369.14 | 13369.14 | 431.73 | <0.0001 |
| Alto x A | 1 | 2848.89 | 2848.89 | 92.00 | <0.0001 |
| Barril | 1 | 35.0417 | 35.0417 | 21.5641 | <0.0001 |
| Alto x B | 1 | 594.14 | 594.14 | 19.1865 | <0.0001 |
| A x B | 1 | 135.14 | 135.14 | 4.36 | 0.0413 |
| Alto x A x B | 1 | 1396.89 | 1396.89 | 45.11 | <0.0001 |
| Error | 56 | 1734.12 | 30.97 | ||
| Total | 63 | 221386.91 |
Una interacción de tres vías significa que las interacciones bidireccionales difieren en función del nivel de la tercera variable. La forma habitual de retratar una interacción de tres vías es trazar las interacciones bidireccionales por separado. La figura\(\PageIndex{6}\) muestra\(\text{Barrel (Knurled or Smooth)} \times \text{Assembly (Staked or Spun)}\) por separado para los dos niveles de Forma de Agujero (Hex o Redondo). Para la Forma Hex, hay muy poca interacción con las líneas cercanas a paralelas con una tendencia muy leve a que el efecto de Barril sea más grande para Staked que para Spun. La interacción bidireccional para la Forma Redonda es diferente: El efecto de Barril es mayor para Spun que para Staked. El hallazgo de una interacción de tres vías significativa indica que esta diferencia en las interacciones bidireccionales es significativa.
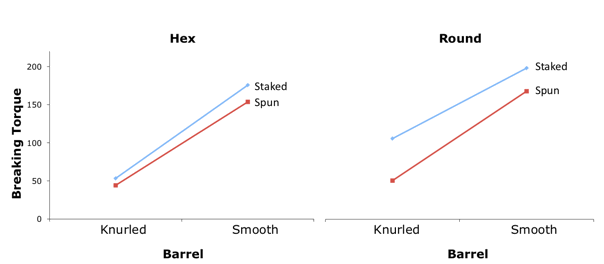
Formateo de Datos para Análisis por Computadora
Los datos en Tabla\(\PageIndex{4}\) han sido reformateados en Tabla\(\PageIndex{7}\). Observe cómo hay una columna para indicar el nivel de resultado y una columna para indicar el nivel de estima. La codificación es la siguiente:
Alta autoestima:\(1\)
Baja autoestima:\(2\)
Éxito:\(1\)
Fracaso:\(2\)
| resultado | estima | attrib |
|---|---|---|
| 1 | 1 | 7 |
| 1 | 1 | 8 |
| 1 | 1 | 7 |
| 1 | 1 | 8 |
| 1 | 1 | 9 |
| 1 | 1 | 5 |
| 1 | 2 | 6 |
| 1 | 2 | 5 |
| 1 | 2 | 7 |
| 1 | 2 | 4 |
| 1 | 2 | 5 |
| 1 | 2 | 6 |
| 2 | 1 | 4 |
| 2 | 1 | 6 |
| 2 | 1 | 5 |
| 2 | 1 | 4 |
| 2 | 1 | 7 |
| 2 | 1 | 3 |
| 2 | 2 | 9 |
| 2 | 2 | 8 |
| 2 | 2 | 9 |
| 2 | 2 | 8 |
| 2 | 2 | 7 |
| 2 | 2 | 6 |
Para usar Analysis Lab para hacer los cálculos, copiaría los datos y luego
- Haga clic en el botón “Ingresar/Editar datos”. (Es posible que se le avise que por razones de seguridad debe usar el método abreviado de teclado para pegar datos).
- Pegue sus datos.
- Haga clic en “Aceptar datos”.
- Haga clic en el botón “Avanzado” junto al botón “ANOVA”.
- Seleccione “attrib” como variable dependiente y tanto “resultado” como “estima” como variables de “grupo”.
- Haga clic en el botón “Hacer ANOVA”.


