Glosario
- Page ID
- 151973
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objetivos de aprendizaje
- Definiciones de diversos términos que ocurren a lo largo del libro de texto
Comparación A Priori/Comparación Planeada
Una comparación que se planifica antes de realizar el experimento o al menos antes de que se examinen los datos. También se llama comparación a priori.
Desviación Absoluta/ Diferencia Absoluta
El valor absoluto de la diferencia entre dos números. La desviación absoluta entre\(5\) y\(3\) es\(2\); entre\(3\) y\(5\) es\(2\); y entre\(-4\) y\(2\) es\(6\).
Hipótesis alternativa
En las pruebas de hipótesis, se plantea la hipótesis nula y una hipótesis alternativa. Si los datos son lo suficientemente fuertes como para rechazar la hipótesis nula, entonces la hipótesis nula es rechazada a favor de una hipótesis alternativa. Por ejemplo, si la hipótesis nula fuera esa\(μ_1= μ_2\) entonces la hipótesis alternativa (para una prueba de dos colas) sería\(μ_1 ≠ μ_2\).
Análisis de varianza
El análisis de varianza es un método para probar hipótesis sobre medias. Es el método de inferencia estadística más utilizado para el análisis de datos experimentales.
Anti-registro
Tomar el anti-log de un número deshace la operación de tomar el registro. Por lo tanto\(\log_{10}(1000)= 3\), ya que, el\(antilog_{10}\) de\(3\) es\(1,000\) .Tomando el anti-log de un número deshace la operación de tomar la bitácora. Por lo tanto\(\log_{10}(1000)= 3\), ya que, el\(antilog_{10}\) de\(3\) es\(1,000\). Tomando el antilog de\(X\) plantea la base del logaritmo en cuestión a\(X\).
Promedio
- La media (aritmética)
- Cualquier medida de tendencia central
Gráfico de barras
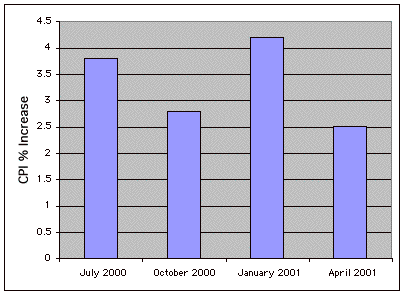
Un método gráfico de presentación de datos. Se dibuja una barra para cada nivel de una variable. La altura de cada barra contiene el valor de la variable. Los gráficos de barras son útiles para mostrar cosas como recuentos de frecuencia y aumentos porcentuales. No se recomiendan para mostrar medios (a pesar de la práctica generalizada) ya que las parcelas de caja presentan más información en la misma cantidad de espacio.
A continuación se muestra un gráfico de barras de ejemplo.
Tasa Base
La verdadera proporción de una población que presenta algún padecimiento, atributo o enfermedad. Por ejemplo, la proporción de personas con esquizofrenia es aproximadamente\(0.01\). Es muy importante considerar la tasa base a la hora de clasificar a las personas. Como dice el refrán, “si escuchas pezuñas, piensa en caballo no en cebra” ya que es más probable que te encuentres con un caballo que con una cebra (al menos en la mayoría de los lugares).
Teorema de Bayes
El teorema de Bayes considera tanto la probabilidad previa de un evento como el valor diagnóstico de una prueba para determinar la probabilidad posterior del evento. El teorema se muestra a continuación:
\[P(D\mid T) = \frac{P(T\mid D)P(D)}{P(T\mid D)P(D)+P(T\mid D')P(D')}\]
donde\(P(D|T)\) es la probabilidad posterior de condición\(D\) dada resultado de prueba\(T\),\(P(T|D)\) es la probabilidad condicional de\(T\) dado\(D\),\(P(D)\) es la probabilidad previa de\(D\),\(P(T|D')\) es la probabilidad condicional de\(T\) dado no\(D\) , y\(P(D')\) es la probabilidad de no\(D'\).
Betacaroteno
El cuerpo humano convierte el betacaroteno en Vitamina\(A\), un componente esencial de nuestras dietas. Muchas verduras, como las zanahorias, son buenas fuentes de betacaroteno. Los estudios han sugerido que los suplementos de betacaroteno pueden proporcionar una variedad de beneficios para la salud, que van desde promover ojos sanos hasta prevenir el cáncer. Otros estudios han encontrado que los suplementos de betacaroteno pueden aumentar la incidencia de cáncer.
Peso beta
Un coeficiente de regresión estandarizado.
Factor entre sujetos/Variable entre sujetos
Las variables entre sujetos son variables independientes o factores en los que se utiliza un grupo diferente de sujetos para cada nivel de la variable. Si se realiza un experimento comparando cuatro métodos de enseñanza de vocabulario y si se utiliza un grupo diferente de asignaturas para cada uno de los cuatro métodos de enseñanza, entonces el método de enseñanza es una variable entre sujetos.
Factor entre sujetos/Variable entre sujetos
Las variables entre sujetos son variables independientes o factores en los que se utiliza un grupo diferente de sujetos para cada nivel de la variable. Si se realiza un experimento comparando cuatro métodos de enseñanza de vocabulario y si se utiliza un grupo diferente de asignaturas para cada uno de los cuatro métodos de enseñanza, entonces el método de enseñanza es una variable entre sujetos.
Sesgo
- Un método de muestreo es sesgado si cada elemento no tiene la misma posibilidad de ser seleccionado. Una muestra de usuarios de Internet encontró que leer un libro de estadísticas en línea sería una muestra sesgada de todos los usuarios de Internet. Una muestra aleatoria es imparcial. Tenga en cuenta que el posible sesgo se refiere al método de muestreo, no al resultado. Un método imparcial podría, por casualidad, conducir a una muestra muy no representativa.
- Un estimador está sesgado si sistemáticamente sobreestima o subestima el parámetro que está estimando. Es decir, está sesgada si la media de la distribución muestral del estadístico no es el parámetro que está estimando, La media muestral es una estimación imparcial de la media poblacional. La desviación cuadrática media de las puntuaciones de la muestra de su media es una estimación sesgada de la varianza, ya que tiende a subestimar la varianza poblacional.
Distribución Bimodal
Una distribución con dos picos distintos. A continuación se muestra un ejemplo.
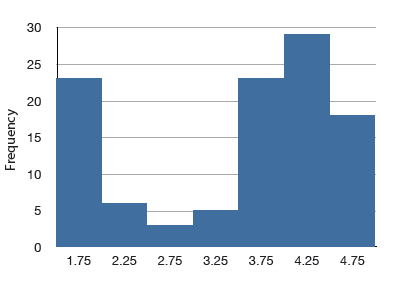
Distribución binomial
Una distribución de probabilidad para eventos independientes para los que solo hay dos resultados posibles, como un giro de moneda. Si uno de los dos resultados se define como un éxito, entonces la probabilidad de exactamente x éxitos fuera de los\(N\) ensayos (eventos) viene dada por:
\[P(x) = \frac{N!}{x!(N-x)!}\pi ^x(1-\pi )^{N-x}\]
Bivariado
Los datos bivariados son datos para los cuales hay dos variables para cada observación. A modo de ejemplo, los siguientes datos bivariados muestran las edades de esposos y esposas de parejas\(10\) casadas.
| Marido | 36 | 72 | 37 | 36 | 51 | 50 | 47 | 50 | 37 | 41 |
| Esposa | 35 | 67 | 33 | 35 | 50 | 46 | 47 | 42 | 36 | 41 |
Corrección de Bonferroni
En general, para mantener la tasa de error familiar (\(FER\)) en o por debajo\(0.05\), la tasa de error por comparación (\(PCER\)) debe ser:\[PCER = 0.05/c\] dónde\(c\) está el número de comparaciones. De manera más general, para asegurar que el\(FER\) es menor o igual a alfa, use\[PCER = alpha/c\]
Parcela de caja
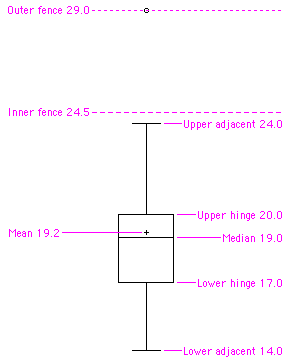
Uno de los resúmenes gráficos más efectivos de un conjunto de datos, la gráfica de caja generalmente muestra media, mediana,\(25^{th}\)\(75^{th}\) percentiles y valores atípicos. Una gráfica de caja estándar se compone de la mediana, bisagra superior, bisagra inferior, valor adyacente superior, valor adyacente inferior, valores externos y valores lejanos. A continuación se muestra un ejemplo. Las gráficas de caja paralelas son muy útiles para comparar distribuciones. Ver también: escalón, H-spread.
Centro (de una distribución)/Tendencia Central
El centro o medio de una distribución. Hay muchas medidas de tendencia central. Los más comunes son la media, mediana y, modo. Otros incluyen la trimedia, la media recortada y la media geométrica).
Frecuencia de clase
Uno de los componentes de un histograma, la frecuencia de clase es el número de observaciones en cada intervalo de clase.
Intervalo de clase/Ancho del compartimento
También conocido como ancho de contenedor, el intervalo de clase es una división de datos para su uso en un histograma. Por ejemplo, es posible dividir las puntuaciones en una prueba de\(100\) puntos en intervalos de clase de\(1-25\)\(26-49\),\(50-74\) y\(75-100\).
Comparación entre medios/ contraste entre medias
Un método para probar las diferencias entre las medias de significancia. Por ejemplo, se podría probar si la diferencia entre\(\text{Mean 1}\) y el promedio de\(\text{Mean 2}\) y\(\text{Mean 3}\) es significativamente diferente.
Probabilidad Condicional
La probabilidad que\(\text{event A}\) ocurre dado que\(\text{event B}\) ya ocurrió se llama la probabilidad condicional de\(A\) dado\(B\). Simbólicamente, esto está escrito como\(P(A|B)\). La probabilidad de que llueva el lunes dado que llovió el domingo estaría escrita como\(\text{P(Rain on Monday | Rain on Sunday)}\).
Intervalo de confianza
Un intervalo de confianza es un rango de puntuaciones que probablemente contengan el parámetro que se estima. Los intervalos se pueden construir para que tengan más o menos probabilidades de contener el parámetro:\(95\%\) de los intervalos de\(95\%\) confianza contienen el parámetro estimado mientras que\(99\%\) de los intervalos de\(99\%\) confianza contienen el parámetro estimado. Cuanto más amplio sea el intervalo de confianza, más incertidumbre hay sobre el valor del parámetro.
Confundir
Dos o más variables se confunden si sus efectos no se pueden separar porque varían juntas. Por ejemplo, si un estudio sobre el efecto de la luz manipulaba inadvertidamente el calor junto con la luz, entonces la luz y el calor serían confundidos.
Cocin's D
La D de Cook es una medida de la influencia de una observación en la regresión y es proporcional a la suma de las diferencias cuadradas entre las predicciones realizadas con todas las observaciones en el análisis y las predicciones realizadas dejando fuera la observación en cuestión.
Constante
Un valor que no cambia. Valores como pi, o la masa de la Tierra son constantes. Comparar con variables.
Variables continuas
Variables que pueden tomar cualquier valor en un cierto rango. El tiempo y la distancia son continuos; el género, la puntuación SAT y el “tiempo redondeado al segundo más cercano” no lo son. Las variables que no son continuas se conocen como variables discretas. Ninguna variable medida es verdaderamente continua; sin embargo, las variables discretas medidas con suficiente precisión a menudo pueden considerarse continuas para fines prácticos.
Prueba t de pares correlacionados/Prueba t de pares relacionados
Una prueba de la diferencia entre medias de dos condiciones cuando hay pares de puntajes. Por lo general, cada par de puntuaciones es de un tema diferente.
Contrapesado
El contrapeso es un método para evitar la confusión entre variables. Considerar un experimento en el que los sujetos se prueben tanto en una tarea de tiempo de reacción auditiva (en la que los sujetos responden a un estímulo auditivo) como en una tarea de tiempo de reacción visual (en la que los sujetos responden a un estímulo visual). A la mitad de los sujetos se les da la tarea visual primero y a la otra mitad de los sujetos se les da primero la tarea auditiva. De esa manera, no hay confusión de orden de presentación y tarea.
Índice de Precios al Consumidor - CPI
También conocido como índice de costo de vida, el IPC es una estadística financiera que mide el cambio en el precio de un grupo representativo de bienes a lo largo del tiempo.
Variable de criterio
En el análisis de regresión (como la regresión lineal) la variable criterio es la variable que se predice. En general, la variable criterio es la variable dependiente.
Distribución Acumulada de Frecuencia
Una distribución que muestra el número de observaciones menor o igual que los valores en el\(X\) eje. La siguiente gráfica muestra una distribución acumulativa para las puntuaciones de una prueba.
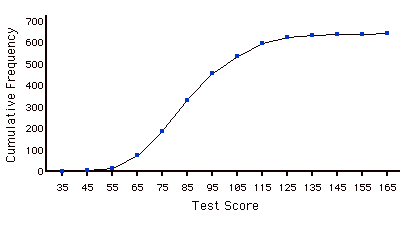
Polígono Acumulado de Frecuencia
Polígono de frecuencia cuyos vértices representan la suma de todas las frecuencias de clase anteriores de los datos. Por ejemplo, si un polígono de frecuencia tuviera vértices de\(5, 8, 3, 7, 10\), el polígono de frecuencia acumulada en los mismos datos tendría vértices de\(5, 13, 16, 23, 33\). Como otro ejemplo, a continuación se muestra una distribución de frecuencia acumulativa para las puntuaciones en una prueba de psicología.
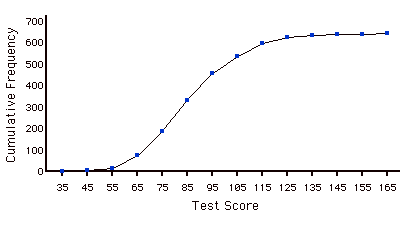
Datos
Una colección de valores para ser utilizados para el análisis estadístico.
Variable dependiente
Una variable que mide el resultado experimental. En la mayoría de los experimentos se observan los efectos de la variable independiente sobre las variables dependientes. Por ejemplo, si un estudio investigara la efectividad de un tratamiento experimental para la depresión, entonces la medida de la depresión sería la variable dependiente.
Sinónimo: medida dependiente
Estadística Descriptiva
- La rama de la estadística se ocupa de describir y resumir datos.
- Un conjunto de estadísticas como la media, desviación estándar y sesgo que describen una distribución.
Puntuaciones de desviación
Puntuaciones que se expresan como diferencias (desviaciones) de algún valor, generalmente la media. Convertir datos en puntuaciones de desviación normalmente significa restar la puntuación media de la puntuación de la otra. Así, los valores\(1\),\(2\), y\(3\) en forma de desviación-puntuación se computarían restando la media\(2\) de cada valor y serían\(-1, 0, 1\).
Grados de Libertad - df
Los grados de libertad de una estimación es el número de piezas de información independientes que entran en la estimación. En general, los grados de libertad para una estimación son iguales al número de valores menos el número de parámetros estimados en ruta a la estimación en cuestión. Por ejemplo, para estimar la varianza poblacional, primero se debe estimar la media poblacional. Por lo tanto, si la estimación de varianza se basa en\(N\) observaciones, hay\(N - 1\) grados de libertad.
Variable Discreta
Las variables que solo pueden tomar un número finito de valores se denominan “variables discretas”. Todas las variables cualitativas son discretas. Algunas variables cuantitativas son discretas, como el rendimiento calificado como\(1\),\(2\),\(3\), o\(4\)\(5\), o la temperatura redondeada al grado más cercano. En ocasiones, una variable que adquiere suficientes valores discretos puede considerarse continua para fines prácticos. Un ejemplo es el tiempo hasta el milisegundo más cercano.
Las variables que pueden tomar un número infinito de valores posibles se denominan “variables continuas”.
Distribución/Distribución de frecuencia
La distribución de datos empíricos se denomina distribución de frecuencia y consiste en un recuento del número de ocurrencias de cada valor. Si los datos son continuos, entonces se usa una distribución de frecuencia agrupada. Normalmente, una distribución se representa usando un polígono de frecuencia o un histograma.
Las ecuaciones matemáticas se utilizan a menudo para definir distribuciones. La distribución normal es, quizás, el ejemplo más conocido. Muchas distribuciones empíricas son aproximadas bien por distribuciones matemáticas como la distribución normal.
Valor esperado
El valor esperado de un estadístico es la media de la distribución muestral del estadístico. Se puede pensar vagamente como el valor promedio a largo plazo de la estadística.
Variables factoriales/independientes
Variables que son manipuladas por el experimentador, a diferencia de las variables dependientes. La mayoría de los experimentos consisten en observar el efecto de las variables independientes sobre las variables dependientes.
Diseño Factorial
En un diseño factorial, cada nivel de cada variable independiente se empareja con cada nivel de cada otra variable independiente. Así, un diseño\(2 \times 3\) factorial consiste en las\(6\) posibles combinaciones de los niveles de las variables independientes.
Falso Positivo
Un falso positivo ocurre cuando un procedimiento diagnóstico devuelve un resultado positivo mientras que el verdadero estado del sujeto es negativo. Por ejemplo, si una prueba de estreptococo dice que el paciente tiene estreptococos cuando en realidad no lo hace, entonces el error en el diagnóstico se llamaría falso positivo. En algunos contextos, un falso positivo se llama falsa alarma. El concepto es similar a un error Tipo I en las pruebas de significancia.
Tasa de error familiar
Cuando se realiza una serie de pruebas de significancia, la tasa de error familiar (\(FER\)) es la probabilidad de que una o más de las pruebas de significancia den como resultado un error de Tipo I.
Valor lejano
Uno de los componentes de una gráfica de caja, valores lejanos son aquellos que están a más de\(2\) pasos de la bisagra más cercana. Están más allá de las cercas exteriores.
Resultado Favorable
Un resultado favorable es el resultado de interés. Por ejemplo se podría definir un resultado favorable en el volteo de una moneda como cabeza. El término “resultado favorable” no significa necesariamente que el resultado sea deseable; en algunos experimentos, el resultado favorable podría ser el fracaso de una prueba, o la ocurrencia de un evento indeseable.
Distribución de frecuencia
Para una variable discreta, una distribución de frecuencia consiste en la distribución del número de ocurrencias para cada valor de la variable. Para una variable continua, es el número de ocurrencias para una variedad de rangos de variables.
Polígono de frecuencia
Un polígono de frecuencia es una representación gráfica de una distribución. Particiona la variable en el\(x\) eje en varios intervalos de clase contiguos de (generalmente) anchos iguales. Las alturas de los puntos del polígono representan las frecuencias de clase.
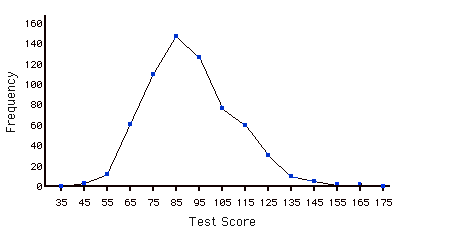
Tabla de frecuencias
Una tabla que contiene el número de ocurrencias en cada clase de datos; por ejemplo, el número de cada color de M&Ms en una bolsa. Tablas de frecuencia utilizadas a menudo para crear histogramas y polígonos de frecuencia. Cuando se crea una tabla de frecuencias para una variable cuantitativa, generalmente se usa una tabla de frecuencias agrupadas.
Tabla de frecuencias agrupadas
Una tabla de frecuencias agrupadas muestra el número de valores para diversos rangos de puntuaciones. A continuación se muestra una tabla de frecuencias agrupadas para tiempos de respuesta (en milisegundos) para una tarea motora simple.
| Rango | Frecuencia |
| 500-600 | 3 |
| 600-700 | 6 |
| 700-800 | 5 |
| 800-900 | 5 |
| 900-1000 | 0 |
| 1000-1100 | 1 |
Media Geométrica
La media geométrica es una medida de tendencia central. La media geométrica de n números se obtiene multiplicando todos ellos juntos, y luego tomando la\(n^{th}\) raíz de ellos. Por ejemplo, para los números\(1\),\(10\), y\(100\), el producto de todos los números es:\(1 \times 10 \times 100 = 1,000\). Dado que hay tres números, tomamos la raíz en cubos del producto (\(1,000\)) que es igual a\(10\).
Gráficos/ Gráficos
Las gráficas suelen ser la forma más efectiva de describir distribuciones y relaciones entre variables. Entre las gráficas más comunes se encuentran los histogramas, las gráficas de caja, las gráficas de barras y las gráficas de dispersión.
Distribución de frecuencia agrupada
Una distribución de frecuencia agrupada es una distribución de frecuencia en la que las frecuencias se muestran para rangos de datos en lugar de para valores individuales. Por ejemplo, la distribución de alturas podría calcularse definiendo rangos de una pulgada. Entonces se tabularía la frecuencia de individuos con varias alturas redondeadas a la pulgada más cercana.
Media armónica
La media armónica de n números (\(X_1\)a\(X_n\)) se calcula usando la siguiente fórmula:
\[\mathit{Harmonic\; Mean} = \frac{n}{\tfrac{1}{x_1}+\tfrac{1}{x_2}+\cdots +\tfrac{1}{x_n}}\]
A menudo se calcula la media armónica de los tamaños de muestra.
Histograma
Un histograma es una representación gráfica de una distribución. Particiona la variable en el\(x\) eje en varios intervalos de clase contiguos de (generalmente) anchos iguales. Las alturas de las barras representan las frecuencias de clase.
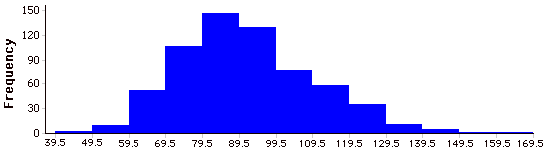
Efecto Historia
Un problema de confusión donde el paso del tiempo, y no la variable de interés, es responsable de los efectos observados.
Homogeneidad de varianza
El supuesto de que las varianzas de todas las poblaciones son iguales.
Homocedasticidad
En regresión lineal, se supone que la varianza alrededor de la línea de regresión es la misma para todos los valores de la variable predictora.
H-spread
Uno de los componentes de una gráfica de caja, el\(H\) -spread es la diferencia entre la bisagra superior y la bisagra inferior.
iMac
Una línea de computadoras lanzadas por Apple en\(1998\), que intentó hacer que las computadoras fueran más accesibles (mayor facilidad de uso) y de moda (venían en una línea de colores de diseñador).
Independencia
Se dice que dos variables son independientes si el valor de una variable no proporciona información sobre el valor de la otra variable. Estas dos variables no estarían correlacionadas de manera que la r de Pearson estaría\(0\).
Dos eventos son independientes si la probabilidad de que ocurra el segundo evento es la misma independientemente de si ocurrió o no el primer evento.
Eventos Independientes
Los eventos\(A\) y\(B\) son eventos independientes si la probabilidad de\(B\) que ocurra el Evento es la misma independientemente de que\(A\) ocurra o no el Evento. Por ejemplo, si lanzas dos dados, la probabilidad de que aparezca el segundo dado\(1\) es independiente de si salió el primer dado\(1\). Formalmente, esto se puede afirmar en términos de probabilidades condicionales:
\[P(A|B) = P(A)\\ P(B|A) = P(B)\]
Inferencia
El acto de sacar conclusiones sobre una población a partir de una muestra.
Estadísticas Inferenciales
La rama de la estadística se ocupa de sacar conclusiones sobre una población a partir de una muestra. Esto generalmente se realiza a través de muestreo aleatorio, seguido de inferencias hechas sobre la tendencia central, o cualquiera de una serie de otros aspectos de una distribución.
Influencia
Influencia se refiere al grado en que una sola observación en regresión influye en la estimación de los parámetros de regresión. A menudo se mide en términos cuánto diferirían los puntajes previstos para otras observaciones si no se incluyera la observación en cuestión.
Barja Interior
En una gráfica de caja, la cerca interior inferior está un paso por debajo de la bisagra inferior mientras que la valla interior superior está un paso por encima de la bisagra superior.
Interacción
Dos variables independientes interactúan si el efecto de una de las variables difiere dependiendo del nivel de la otra variable.
Gráfica de interacción
Una gráfica de interacción muestra los niveles de una variable en el\(X\) eje y tiene una línea separada para las medias de cada nivel de la otra variable. El\(Y\) eje es la variable dependiente. Una mirada a esta gráfica muestra que el efecto de la dosis es diferente para los machos que para las hembras.
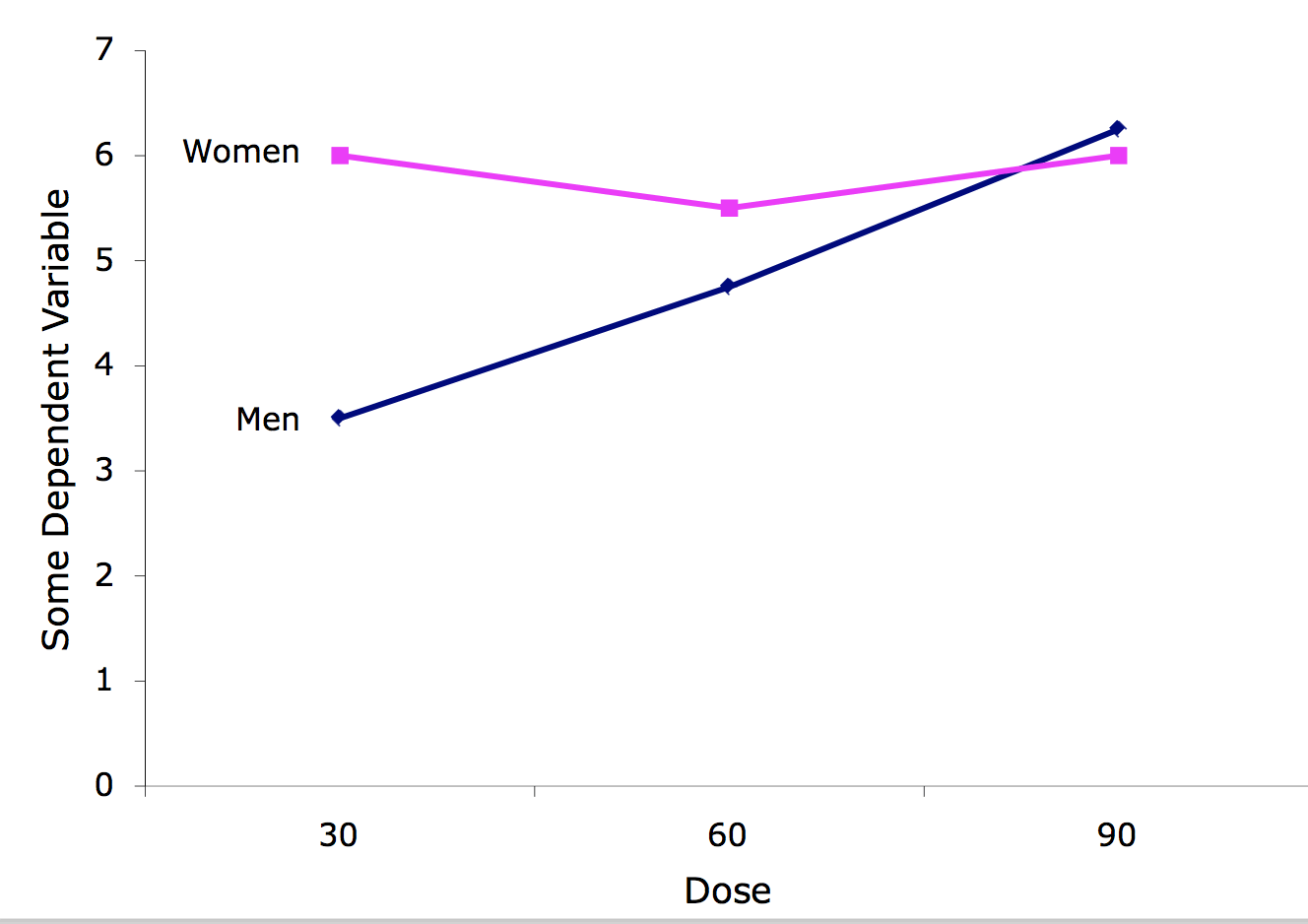
Gama Intercuartil
El Rango Intercuartílico (\(IQR\)) es el (\(75^{th}\)percentil —\(25^{th}\) percentil). Es una medida robusta de variabilidad.
Estimación de Intervalos
Una estimación de intervalo es un rango de puntuaciones que probablemente contengan el parámetro estimado.
Balanzas Intervaladas
Una de\(4\) Niveles de Medición, las escalas de intervalo son escalas numéricas en las que los intervalos tienen la misma interpretación en todo momento. Como ejemplo, considere la escala de temperatura Fahrenheit. La diferencia entre\(30\) grados y\(40\) grados representa la misma diferencia de temperatura que la diferencia entre\(80\) grados y\(90\) grados. Esto se debe a que cada intervalo de\(10\) grados tiene el mismo significado físico (en términos de la energía cinética. A diferencia de las escalas de relación, las escalas de intervalo no tienen un verdadero punto cero.
Jitter
Cuando los puntos de una gráfica están fluctuados, los se mueven horizontalmente para que todos los puntos se puedan ver y ninguno se oculte debido a valores superpuestos. A continuación se muestra un ejemplo:
Curtosis
La curtosis mide qué tan gordas o delgadas son las colas de una distribución en relación con una distribución normal. Se define comúnmente como:
\[\sum \frac{(X-\mu )^4}{\sigma ^4} - 3\]
Las distribuciones con colas largas se llaman leptokúrticas; las distribuciones con colas cortas se llaman platykurtic. Las distribuciones normales tienen cero curtosis.
Leptoúrtico
Una distribución con colas largas en relación con una distribución normal es leptoúrtica.
Nivel/Nivel de una variable/Nivel de un factor
Cuando un factor consiste en diversas condiciones de tratamiento, cada condición de tratamiento se considera un nivel de ese factor. Por ejemplo, si el factor fuera la dosis del fármaco, y se probaron tres dosis, entonces cada dosis sería un nivel del factor y el factor tendría tres niveles.
Niveles de medición
Las escalas de medición difieren en su nivel de medición. Hay cuatro niveles comunes de medición:
- Las escalas nominales son solo etiquetas.
- Las Escalas Ordinales están ordenadas pero no son realmente cuantitativas. Los intervalos iguales en la escala ordinal no implican intervalos iguales en el rasgo subyacente.
- Las escalas de intervalo están ordenadas e intervalos iguales intervalos iguales en el rasgo subyacente. Sin embargo, las escalas de intervalo no tienen un verdadero punto cero.
- Las escalas de relación son escalas de intervalo que tienen un verdadero punto cero. Con escalas de relación, es sensato hablar de que un valor sea el doble de grande que otro, por ejemplo.
Apalancamiento
El apalancamiento es un factor que afecta la influencia de una observación en la regresión. El apalancamiento se basa en cuánto difiere el valor de la observación en la variable predictora de la media de la variable predictora. Cuanto mayor sea el apalancamiento de una observación, más potencial tiene para ser una observación influyente.
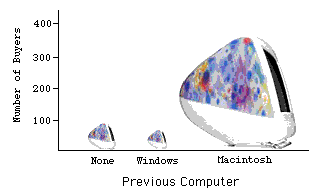
Factor de Mentira
Muchos problemas pueden surgir cuando se utilizan gráficos elegantes sobre los planos. Las distorsiones pueden ocurrir cuando se utilizan las alturas de los objetos para indicar el valor porque la mayoría de las personas prestarán atención a las áreas de los objetos en lugar de a su altura. El factor mentira es la relación entre el efecto aparente en la gráfica y el efecto real en los datos; si se desvía en más\(0.05\) de\(1\), la gráfica es generalmente inaceptable. El factor mentira en la siguiente gráfica es casi\(6\).
Mentiras
Hay tres tipos de mentiras:
- mentiras regulares
- malditas mentiras
- estadísticas
Esto es según Benjamin Disraeli citado por Mark Twain.
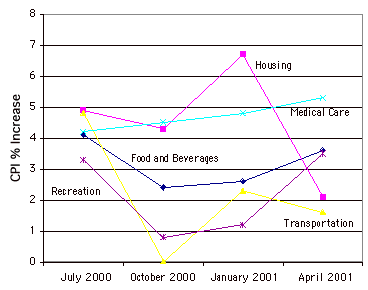
Gráfico de líneas
Esencialmente un gráfico de barras en el que la altura de cada par está representada por un solo punto, con cada uno de estos puntos conectados por una línea. Los gráficos de líneas se utilizan mejor para mostrar el cambio a lo largo del tiempo, y nunca deben usarse si su\(X\) eje no es una variable ordenada. A continuación se muestra un ejemplo.
Combinación Lineal
Una combinación lineal de variables es una forma de crear una nueva variable combinando otras variables. Una combinación lineal es aquella en la que cada variable se multiplica por un coeficiente y se suman los productos son. Por ejemplo, si
\[Y = 3X_1 + 2X_2 + 0.5X_3\]
entonces\(Y\) es una combinación lineal de las variables\(X_1\),\(X_2\), y\(X_3\).
Regresión lineal
La regresión lineal es un método para predecir una variable criterio a partir de una o más variables predictoras. En regresión simple, el criterio se predice a partir de una única variable predictora y la línea recta que mejor se ajusta es de la forma:
\[Y' = bX + A\]
donde\(Y'\) está la puntuación predicha,\(X\) es la variable predictora,\(b\) es la pendiente y\(A\) es la\(Y\) intersección. Normalmente, el criterio para la línea de “mejor ajuste” es la línea para la que se minimiza la suma de los errores cuadrados de predicción. En regresión múltiple, el criterio se predice a partir de dos o más variables predictoras.
Relación Lineal
Existe una relación lineal perfecta entre dos variables si una gráfica de dispersión de los puntos cae sobre una línea recta. La relación es lineal aunque los puntos diverjan de la línea siempre que la divergencia sea aleatoria en lugar de sistemática.
Transformación Lineal
Una transformación lineal es cualquier transformación de una variable que se puede lograr multiplicándola por una constante, y luego sumando una segunda constante. Si\(Y\) es el valor transformado de\(X\), entonces\(Y = aX + b\). La transformación de grados Fahrenheit a grados centígrados es lineal y se realiza usando la fórmula:
\[C = 0.55556F - 17.7778\]
Logaritmo - Log
El logaritmo de un número es la potencia a la que se tiene que elevar la base del logaritmo para igualar el número. Si la base del logaritmo es\(10\) y el número es\(1,000\) entonces el log es\(3\) ya que\(10\) tiene que elevarse a la\(3^{rd}\) potencia para igualar\(1,000\).
Valor adyacente inferior
Un componente de una gráfica de caja, el valor adyacente inferior es el valor más pequeño en los datos por encima de la cerca inferior interna.
Bisagra Inferior
Componente de una gráfica de caja, la bisagra inferior es el\(25^{th}\) percentil. La bisagra superior es el\(75^{th}\) percentil.
M & M
Un tipo de caramelo que consiste en chocolate dentro de una cáscara. Las M & M vienen en una variedad de colores.
Efecto Principal
Un efecto principal de una variable independiente es el efecto de la variable promediando sobre todos los niveles de la otra (s) variable (s). Por ejemplo, en un diseño con la edad y el género como factores, el principal efecto del género sería la diferencia entre los géneros promediando a través de todas las edades utilizadas en el experimento.
Margen de Error
Cuando se utiliza una estadística para estimar un parámetro, es común calcular un intervalo de confianza. El margen de error es la diferencia entre la estadística y los puntos finales del intervalo. Por ejemplo, si la estadística fuera\(0.6\) y el intervalo de confianza variaba de\(0.4\) a\(0.8\), entonces el margen de error sería\(0.20\). A menos que se especifique lo contrario, se utiliza el intervalo de\(95\%\) confianza.
Media Marginal
En un diseño con dos factores, las medias marginales para un factor son las medias para ese factor promediadas en todos los niveles del otro factor. En la tabla que se muestra a continuación, los dos factores son “Relación” y “Peso acompañante”. Las medias marginales para cada uno de los dos niveles de Relación (Amiga y Conocido) se calculan promediando a través de los dos niveles de Peso Acompañante. Así, la media marginal para Conocimientos de\(6.37\) es la media de\(6.15\) y\(6.59\).
|
Peso acompañante
|
||||
|
|
Obesos
|
Típico
|
Media Marginal
|
|
| Relación |
Amiga
|
5.65
|
6.19
|
5.92
|
|
Conocido
|
6.15
|
6.59
|
6.37
|
|
|
Media Marginal
|
5.90
|
6.39
|
||
Media/Media Aritmética
También conocida como media aritmética, la media es típicamente lo que se entiende por la palabra “promedio”. La media es quizás la medida más común de tendencia central. La media de una variable viene dada por (la suma de todos sus valores)/(el número de valores). Por ejemplo, la media de\(4\),\(8\), y\(9\) es\(7\). La media de la muestra se escribe como M, y la media de la población como la letra griega mu (\(μ\)). A pesar de su popularidad, la media puede no ser una medida apropiada de tendencia central para distribuciones sesgadas, o en situaciones con valores atípicos.
Mediana
La mediana es una medida popular de tendencia central. Es el\(50^{th}\) percentil de una distribución. Para encontrar la mediana de una serie de valores, primero ordenarlos, luego encontrar la observación en el medio: la mediana de\(5, 2, 7, 9, 4\) es\(5\). (Tenga en cuenta que si hay un número par de valores, uno toma el promedio de los dos medios: la mediana de\(4, 6, 8,10\) es\(7\).) La mediana suele ser más apropiada que la media en distribuciones sesgadas y en situaciones con valores atípicos.
Señorita
Las faltas ocurren cuando una prueba diagnóstica devuelve un resultado negativo, pero el verdadero estado del sujeto es positivo. Por ejemplo, si una persona tiene faringitis estreptocócica y la prueba diagnóstica no lo indica, entonces se ha producido una falla. El concepto es similar a un error Tipo II en las pruebas de significancia.
Modo
El modo es una medida de tendencia central. Es el valor más frecuente en una distribución: el modo de\(3, 4, 4, 5, 5, 5, 8\) es\(5\). Tenga en cuenta que el modo puede ser muy diferente de la media y la mediana.
Regresión Múltiple
La regresión múltiple es la regresión lineal en la que se utilizan dos o más variables predictoras para predecir el criterio.
Asociación Negativa
Hay una asociación negativa entre las variables\(X\) y\(Y\) si los valores más pequeños de\(X\) se asocian con valores más grandes de\(Y\) y los valores más grandes de\(X\) se asocian con valores más pequeños de\(Y\).
Escala Nominal
Una escala nominal es uno de los cuatro niveles de medición comúnmente utilizados. No hay orden implícito, y la adición/resta y multiplicación/división serían inapropiadas para una variable en una escala nominal. {Femenino, Masculino} y {Budista, Cristiano, Hindú, Musulmán} no tienen orden natural (excepto alfabético). Ocasionalmente, los valores numéricos son nominales: por ejemplo, si una variable se codificó como\(\text{Female = 1, Male = 2}\), el conjunto\({1,2}\) sigue siendo nominal.
No representante
Una muestra no representativa es una muestra que no refleja con precisión la población.
Distribución Normal
Una de las distribuciones continuas más comunes, una distribución normal a veces se conoce como una “distribución en forma de campana”. Si\(μ\) es la media de distribución, y\(σ\) la desviación estándar, entonces la distribución normal de altura (ordenada) viene dada por
\[\frac{1}{\sqrt{2\pi \sigma ^2}}e^{\tfrac{-(x-\mu )^2}{2\sigma ^2}}\]
A continuación se muestra una gráfica de una distribución normal con una media de\(50\)\(10\) y una desviación estándar de.
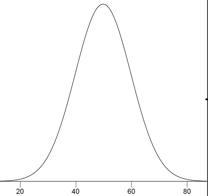
Si la media es\(0\) y la desviación estándar es\(1\), la distribución se conoce como la “distribución normal estándar”.
Hipótesis nula
Una hipótesis nula es una hipótesis probada en pruebas de significancia. Por lo general, es la hipótesis de que un parámetro es cero o que una diferencia entre parámetros es cero. Por ejemplo, la hipótesis nula podría ser que la diferencia entre medias poblacionales es cero. Los experimentadores suelen diseñar experimentos para permitir que se rechace la hipótesis nula.
Hipótesis nula Omninus
La hipótesis nula de que todas las medias poblacionales son iguales.
Prueba de una cola/Probabilidad de una cola/Prueba direccional
El último paso en las pruebas de significancia implica calcular la probabilidad de que un estadístico difiera tanto o más del parámetro especificado en la hipótesis nula como lo hacen las estadísticas obtenidas en el experimento.
Una probabilidad calculada considerando diferencias en una sola dirección, tal como que la estadística es mayor que el parámetro, se denomina probabilidad de una cola. Por ejemplo, si un parámetro es\(0\) y la estadística es\(12\), una probabilidad de una cola (la cola positiva) sería la probabilidad de que un estadístico sea\(≥12\). Comparar con la probabilidad de dos colas que sería la probabilidad de ser cualquiera\(≤ -12\) o\(≥12\).
Escala Ordinal
Uno de los cuatro niveles de medición comúnmente utilizados, una escala ordinal es un conjunto de valores ordenados. Sin embargo, no hay distancia establecida entre los valores de escala. Por ejemplo, para la escala: (Muy Pobre, Pobre, Promedio, Bueno, Muy Bueno) es una escala ordinal. Puede asignar valores numéricos a una escala ordinal: calificación de desempeño como\(1\) para “Muy Pobre”,\(2\) para “Pobre”, etc., pero no hay garantía de que la diferencia entre una puntuación de\(1\) y\(2\) signifique lo mismo que la diferencia entre una puntuación de\(2\) y \(3\).
Comparaciones ortogonales
Cuando las comparaciones entre medias proporcionan información completamente independiente, las comparaciones se denominan “ortogonales”. Si se realizara un experimento con cuatro grupos, entonces una comparación de\(\text{Groups 1 and 2}\) sería ortogonal a una comparación de\(\text{Groups 3 and 4}\) ya que no hay nada en la comparación de\(\text{Groups 1 and 2}\) que proporcione información sobre la comparación de\(\text{Groups 3 and 4}\).
Cerco Exterior
En una gráfica de caja, la cerca exterior inferior está\(2\) escalonada por debajo de la bisagra inferior mientras que la valla interior superior está\(2\) escalonada por encima de la bisagra superior.
Valor atípico
Los valores atípicos son observaciones atípicas, poco frecuentes; valores que tienen una desviación extrema del centro de la distribución. No existe un criterio universalmente acordado para definir un valor atípico, y los valores atípicos solo deben descartarse con extrema precaución. Sin embargo, siempre se deben evaluar los efectos de los valores atípicos en las conclusiones estadísticas.
Valor Exterior
Un componente de una gráfica de caja, los valores externos son más que un\(1\) paso más allá de la bisagra más cercana. Están más allá de una barda interior pero no más allá de una valla exterior.
Comparaciones por pares
Las comparaciones por pares son comparaciones entre pares de medias.
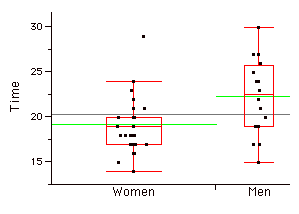
Parcelas de Caja Paralelas
Dos o más parcelas de caja dibujadas en el mismo\(Y\) eje. Estos suelen ser útiles para comparar características de distribuciones. A continuación se muestra un ejemplo que retrata las veces que tomó muestras de mujeres y hombres para realizar una tarea.
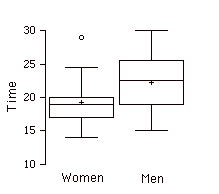
Parámetro
Un valor calculado en una población. Por ejemplo, la media de los números en una población es un parámetro. Comparar con una estadística, que es un valor calculado en una muestra para estimar un parámetro.
Talud parcial
La pendiente parcial en regresión múltiple es la pendiente de la relación entre una variable predictora que es independiente de las otras variables predictoras y el criterio. También es el coeficiente de regresión para la variable predictora en cuestión.
Correlación de momento de producto de Pearson\(r\)/Pearson/Correlación de Pearson
La correlación de Pearson es una medida de la fuerza de la relación lineal entre dos variables. Va desde\(-1\) una relación negativa perfecta hasta\(+1\) una relación positiva perfecta. Una correlación de\(0\) significa que no hay relación lineal.
Percentil
No existe una definición universalmente aceptada de un percentil. Usando el\(65^{th}\) percentil como ejemplo, algunos estadísticos definen el\(65^{th}\) percentil como la puntuación más baja que es mayor que la\(65\%\) de las puntuaciones. Otros han definido el\(65^{th}\) percentil como la puntuación más baja que es mayor o igual a la\(65\%\) de las puntuaciones. A continuación se da una definición más sofisticada. El primer paso es calcular el rango (\(R\)) del percentil en cuestión. Esto se hace usando la siguiente fórmula:
\[R = \frac{P}{100} \times (N + 1)\]
donde\(P\) está el percentil deseado y\(N\) es el número de números. Si\(R\) es un número entero, entonces el\(P^{th}\) percentil es el número con rango\(R\). Cuando no\(R\) es un entero, calculamos el\(P^{th}\) percentil por interpolación de la siguiente manera:
- Definir\(IR\) como la porción entera de\(R\) (el número a la izquierda del punto decimal).
- Definir\(FR\) como la porción fraccionaria o\(R\).
- Encuentra las puntuaciones con Rank\(IR\) y con Rank\(IR + 1\).
- Interpolar multiplicando la diferencia entre las puntuaciones por\(FR\) y sumar el resultado a la puntuación más baja.
Tasa de error por comparación
La tasa de error por comparación se refiere a la tasa de error Tipo I de cualquier prueba de significancia realizada como parte de una serie de pruebas de significancia. Así, si\(10\) cada una de las pruebas de\(0.05\) significancia se realizara a nivel de significancia, entonces la tasa de error por comparación sería\(0.05\). Compare con la tasa de error familiar.
Gráfico circular
Una representación gráfica de datos, el gráfico circular muestra frecuencias relativas de clases de datos. Se trata de un círculo cortado en una serie de cuñas, una para cada clase, con el área de cada cuña proporcional a su frecuencia relativa. Los gráficos circulares solo son efectivos para un pequeño número de clases y son una de las representaciones gráficas menos efectivas.
Placebo
Un dispositivo utilizado en ensayos clínicos, el placebo es visualmente indistinguible de la medicación del estudio, pero en realidad no tiene ningún efecto médico (a menudo, una píldora de azúcar). Un grupo de sujetos elegidos al azar toma el placebo, los otros toman uno u otro tipo de medicamento. Esto se hace para evitar confundir los efectos médicos y psicológicos de la droga. Incluso una pastilla de azúcar puede llevar a algunos pacientes a reportar mejoría y efectos secundarios.
Comparación Planeada/Comparación A Priori
Una comparación que se planifica antes de realizar el experimento o al menos antes de que se examinen los datos. También se llama comparación a priori.
Platykurtic
Una distribución con colas cortas en relación con una distribución normal es platykurtic.
Estimación de puntos
Cuando se está estimando un parámetro, la estimación puede ser un solo número o puede ser un rango de números como en un intervalo de confianza. Cuando la estimación es un solo número, la estimación se denomina “estimación puntual”.
Regresión polinomial
La regresión polinómica es una forma de regresión múltiple en la que se utilizan potencias de una variable predictora en lugar de otras variables predictoras. En el siguiente ejemplo, el criterio (\(Y\)) se predice por\(X\),\(X^2\) y,\(X^3\).
\[Y = b_1X + b_2X^2 + b_3X^3 + A\]
Población
Una población es el conjunto completo de observaciones que le interesan a un investigador. Contraste esto con una muestra que es un subconjunto de una población. Una población puede definirse de una manera conveniente para un investigador. Por ejemplo, se podría definir una población como todas las niñas de cuarto grado en Houston, Texas. O bien, una población diferente es el conjunto de todas las niñas de cuarto grado en Estados Unidos. Las estadísticas inferenciales se computan a partir de los datos de la muestra con el fin de hacer inferencias sobre la población.
Asociación Positiva
Existe una asociación positiva entre las variables\(X\) y\(Y\) si los valores más pequeños de\(X\) se asocian con valores más pequeños de\(Y\) y valores mayores de\(X\) se asocian con valores más grandes de\(Y\).
Probabilidad Posterior
La probabilidad posterior de un evento es la probabilidad del evento calculado después de la recolección de nuevos datos. Uno comienza con una probabilidad previa de un evento y lo revisa a la luz de nuevos datos. Por ejemplo, si\(0.01\) de una población tiene esquizofrenia entonces la probabilidad de que una persona dibujada al azar tenga esquizofrenia es\(0.01\). Esta es la probabilidad previa. Si entonces aprendes que su puntaje en un test de personalidad sugiere que la persona es esquizofrénica, ajustarías tu probabilidad en consecuencia. La probabilidad ajustada es la probabilidad posterior.
Poder
En las pruebas de significancia, el poder es la probabilidad de rechazar una hipótesis falsa nula.
Precisión
La precisión de un estadístico se refiere a lo cerca que se espera que esté del parámetro que está estimando. Las estadísticas precisas varían menos de una muestra a otra. La precisión de una estadística suele definirse en términos de error estándar.
Variable predictora
Una variable predictora es una variable utilizada en regresión para predecir otra variable. A veces se le conoce como una variable independiente si se manipula en lugar de solo medir.
Probabilidad previa
La probabilidad previa de un evento es la probabilidad del evento calculado antes de la recolección de nuevos datos. Uno comienza con una probabilidad previa de un evento y lo revisa a la luz de nuevos datos. Por ejemplo, si\(0.01\) de una población tiene esquizofrenia entonces la probabilidad de que una persona dibujada al azar tenga esquizofrenia es\(0.01\). Esta es la probabilidad previa. Si entonces aprendes que esa puntuación en una prueba de personalidad sugiere que la persona es esquizofrénica, ajustarías tu probabilidad en consecuencia. La probabilidad ajustada es la probabilidad posterior.
Función de densidad de probabilidad
Para una variable aleatoria discreta, una distribución de probabilidad contiene la probabilidad de cada resultado posible. Sin embargo, para una variable aleatoria continua, la probabilidad de cualquier resultado es cero (si lo especifica con suficientes decimales). Una función de densidad de probabilidad es una fórmula que se puede utilizar para calcular las probabilidades de un rango de resultados para una variable aleatoria continua. La suma de todas las densidades es siempre\(1.0\) y el valor de la función siempre es mayor o igual a cero.
Distribución de probabilidad
Para una variable aleatoria discreta, una distribución de probabilidad contiene la probabilidad de cada resultado posible. La suma de todas las probabilidades es siempre\(1.0\).
Probabilidad Valor/\(p\)valor
En las pruebas de significancia, el valor de probabilidad (a veces llamado el\(p\) valor) es la probabilidad de obtener una estadística tan diferente o más diferente del parámetro especificado en la hipótesis nula como el estadístico obtenido en el experimento. El valor de probabilidad se calcula asumiendo que la hipótesis nula es verdadera. Cuanto menor sea el valor de probabilidad, más fuerte será la evidencia de que la hipótesis nula es falsa. Tradicionalmente, la hipótesis nula es rechazada si el valor de probabilidad está por debajo\(0.05\).
Los valores de probabilidad pueden ser de una cola o dos colas.
Variables cualitativas/ Variable categórica
También conocidas como variables categóricas, las variables cualitativas son variables sin sentido natural de orden. Por lo tanto, se miden en una escala nominal. Por ejemplo, el color del cabello (Negro, Marrón, Gris, Rojo, Amarillo) es una variable cualitativa, como lo es el nombre (Adam, Becky, Christina, Dave.). Las variables cualitativas se pueden codificar para que aparezcan numéricas pero sus números no tienen sentido, como en\(\text{male=1, female=2}\). Las variables que no son cualitativas se conocen como variables cuantitativas.
Variable cuantitativa
Variables que se miden en una escala numérica o cuantitativa. Las escalas ordinales, de intervalo y de relación son cuantitativas. La población de un país, la talla de zapatos de una persona o la velocidad de un automóvil son variables cuantitativas. Las variables que no son cuantitativas se conocen como variables cualitativas.
Asignación Aleatoria
La asignación aleatoria ocurre cuando los sujetos en un experimento son asignados aleatoriamente a condiciones. La asignación aleatoria evita la confusión sistemática de los efectos del tratamiento con otras variables.
Muestreo aleatorio/Muestreo aleatorio simple
El proceso de selección de un subconjunto de una población con fines de inferencia estadística. Muestreo aleatorio significa que cada miembro de la población tiene la misma probabilidad de ser elegido.
Rango
La diferencia entre los valores máximo y mínimo de una variable o distribución. El rango es la medida más simple de variabilidad.
Escala de Ratio
Uno de los cuatro niveles básicos de medición, una escala de ratio es una escala numérica con un verdadero punto cero y en la que un intervalo de tamaño dado tiene la misma interpretación para toda la escala. El peso es una escala de ratio, por lo tanto, es significativo decir que una persona\(200\) libra pesa el doble que una persona\(100\) libra.
Regresión
Regresión significa “predicción”. La regresión de\(Y\) on\(X\) significa la predicción de\(Y\) by\(X\).
Coeficiente de regresión
Un coeficiente de regresión es la pendiente de la línea de regresión en regresión simple o la pendiente parcial en regresión múltiple.
Línea de Regresión
En regresión lineal, la línea de mejor ajuste se llama la línea de regresión.
Frecuencia relativa
La proporción de observaciones que caen dentro de una clase determinada. Por ejemplo, si una bolsa de\(55\) M & M's tiene M&M's\(11\) verdes, entonces la frecuencia de M&M verdes es\(11\) y la frecuencia relativa es\(11/55 = 0.20\). Frecuencias relativas se utilizan a menudo en histogramas, gráficos circulares y gráficos de barras.
Distribución de frecuencia relativa
Una distribución de frecuencia relativa es como una distribución de frecuencia excepto que consiste en las proporciones de ocurrencias en lugar de los números de ocurrencias para cada valor (o rango de valores) de una variable.
Confiabilidad
Aunque hay muchas formas de concebir la confiabilidad de una prueba, la forma clásica es definir la confiabilidad como la correlación entre dos formas paralelas de la prueba. Cuando se define de esta manera, la confiabilidad es la relación de varianza de puntaje real a varianza de puntaje de prueba. Chronbach\(α\) es una medida común de confiabilidad.
Factor de medidas repetidas/ Variable de medidas repetidas/ Factor dentro de sujetos /Variable dentro de sujetos
Una variable dentro de los sujetos es una variable independiente que se manipula probando cada sujeto en cada nivel de la variable. Comparar con una variable entre sujetos en la que se utilizan diferentes grupos de sujetos para cada nivel de la variable.
Muestra Representativa
Una muestra representativa es una muestra elegida para que coincida con las cualidades de la población de la que se extrae. Con un tamaño de muestra grande, el muestreo aleatorio se aproximará a una muestra representativa; el muestreo aleatorio estratificado puede ser utilizado para hacer una muestra pequeña más representativa.
Robusto
Algo es robusto si aguanta bien ante la adversidad. Una medida de tendencia central o variabilidad se considera robusta si no se ve muy afectada por algunas puntuaciones extremas. Una prueba estadística se considera robusta si funciona bien a pesar de violaciones moderadas de los supuestos en los que se basa.
Muestra
Una muestra es un subconjunto de una población, a menudo tomada con fines de inferencia estadística. Generalmente, se usa una muestra aleatoria.
Gráfico de dispersión
Un diagrama de dispersión de dos variables muestra los valores de una variable en el\(Y\) eje y los valores de la otra variable en el\(X\) eje. Los gráficos de dispersión son muy adecuados para revelar la relación entre dos variables. El diagrama de dispersión que se muestra a continuación ilustra la relación entre la fuerza de agarre y la fuerza del brazo en una muestra de trabajadores.
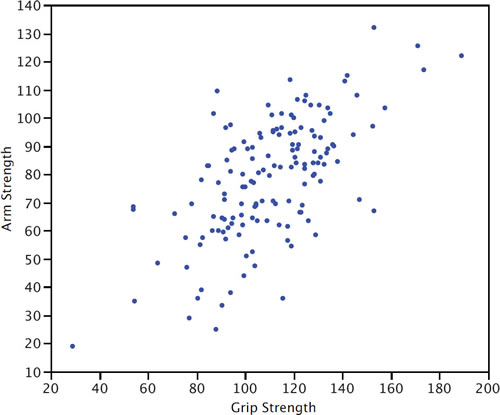
Gama Semi-Intercuartil
El rango semiintercuartílico es el rango intercuartílico dividido por\(2\). Es una medida robusta de variabilidad. El Rango Intercuartílico es el (\(75^{th}\)percentil\(–\)\(25^{th}\) percentil).
Nivel de significancia/nivel A
En las pruebas de significancia, el nivel de significancia es el valor más alto de un valor de probabilidad para el cual se rechaza la hipótesis nula. Los niveles de significancia comunes son\(0.05\) y\(0.01\). Si se usa el\(0.05\) nivel, entonces se rechaza la hipótesis nula si el valor de probabilidad es menor o igual a\(0.05\).
Prueba de significación/Prueba de Hipótesis/Diferencia significativa
Un procedimiento estadístico que pone a prueba la viabilidad de la hipótesis nula. Si los datos (o datos más extremos) son muy improbables dado que la hipótesis nula es verdadera, entonces se rechaza la hipótesis nula. Si los datos o datos más extremos no son improbables, entonces no se rechaza la hipótesis nula. Si se rechaza la hipótesis nula, entonces se dice que el resultado de la prueba es significativo. Un efecto estadísticamente significativo no significa que el efecto sea importante.
Efecto Simple
El efecto simple de un factor es el efecto de ese factor en un solo nivel de otro factor. Por ejemplo, en un diseño con la edad y el género como factores, el efecto de la edad para las mujeres sería uno de los efectos simples de la edad.
Regresión simple
La regresión simple es la regresión lineal en la que se utiliza una variable predictora más para predecir el criterio.
sesgar
Una distribución es sesgada si una cola se extiende más allá de la otra. Una distribución tiene sesgo positivo (está sesgada a la derecha) si la cola a la derecha es más larga. Consulte la gráfica a continuación para ver un ejemplo.
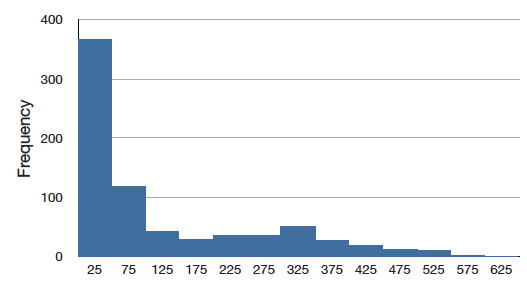
Una distribución tiene un sesgo negativo (está sesgado a la izquierda) si la cola a la izquierda es más larga. Consulte la gráfica a continuación para ver un ejemplo.
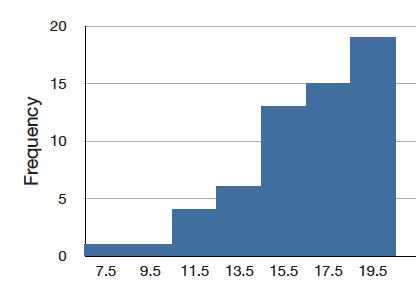
Talud
La pendiente de una línea es el cambio en\(Y\) por cada cambio de una unidad de\(X\). A veces se define como “rise over run” que es lo mismo. La pendiente de la línea negra en la gráfica se\(0.425\) debe a que la línea aumenta\(0.425\) cada vez que\(X\) aumenta en\(1.0\).
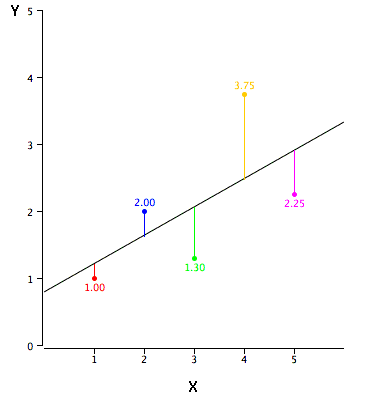
Desviación Cuadrada
Una desviación cuadrada es la diferencia entre dos valores, al cuadrado. El número que minimiza la suma de desviaciones cuadradas para una variable es su media.
Desviación estándar
La desviación estándar es una medida de variabilidad ampliamente utilizada. Se calcula tomando la raíz cuadrada de la varianza. Un atributo importante de la desviación estándar como medida de variabilidad es que si se conoce la media y desviación estándar de una distribución normal, es posible calcular el rango percentil asociado a cualquier puntaje dado.
Error estándar
El error estándar de un estadístico es la desviación estándar de la distribución muestral de ese estadístico. Por ejemplo, el error estándar de la media es la desviación estándar de la distribución muestral de la media. Los errores estándar juegan un papel crítico en la construcción de intervalos de confianza y en las pruebas de significancia.
Error estándar de medición
En la teoría de pruebas, el error estándar de medición es la desviación estándar de las puntuaciones observadas de las pruebas para una puntuación verdadera dada. Por lo general, se estima con la siguiente fórmula en la que\(s\) se encuentra la desviación estándar de los puntajes de las pruebas y\(r\) es la confiabilidad de la prueba.
\[S_{measurement} = s\sqrt{1-r}\]
Error estándar de la media
El error estándar de la media es la desviación estándar de la distribución muestral de la media. La fórmula para el error estándar de la media en una población es:
\[\sigma _m = \frac{\sigma }{\sqrt{N}}\]
donde\(σ\) está la desviación estándar y\(N\) es el tamaño de la muestra. Cuando se calcula en una muestra, la estimación del error estándar de la media es:
\[s_m = \frac{s}{\sqrt{N}}\]
Distribución Normal Estándar
La distribución normal estándar es una distribución normal con una media de\(0\) y una desviación estándar de\(1\).
Puntaje Estándar/Estandarizar/Desviación Normal Estándar/\(Z\)Puntuación
El número de desviaciones estándar una puntuación es de la media de su población. El término “puntaje estándar” se usa generalmente para poblaciones normales; los términos "\(Z\)puntuación” y “desviación normal” solo deben usarse en referencia a distribuciones normales. La transformación de una puntuación en bruto\(X\) a una\(Z\) puntuación se puede hacer usando la siguiente fórmula:
\[Z = \frac{X - \mu}{\sigma }\]
Transformar una variable de esta manera se llama “estandarizar” la variable. Se debe tener en cuenta que si no\(X\) se distribuye normalmente entonces la variable transformada tampoco se distribuirá normalmente.
Estandarizar/Puntaje Estándar
Se estandariza una variable si tiene una media de\(0\) y una desviación estándar de\(1\). La transformación de una puntuación bruta\(X\) a una puntuación estándar se puede hacer usando la siguiente fórmula:
\[X_{standardized} = \frac{X - \mu}{\sigma }\]
donde\(μ\) es la media y\(σ\) es la desviación estándar. Transformar una variable de esta manera se llama “estandarizar” la variable. Se debe tener en cuenta que si no\(X\) se distribuye normalmente entonces la variable transformada tampoco se distribuirá normalmente.
Estadística/Estadística
- Lo que estás estudiando en este momento, también conocido como análisis estadístico, o inferencia estadística. Es un campo de estudio que se ocupa de resumir datos, interpretar datos y tomar decisiones basadas en datos.
- Una cantidad calculada en una muestra para estimar un valor en una población se denomina “estadística”.
Exhibición del tallo y de la hoja
Una representación cuasi-gráfica de datos numéricos. Generalmente, todos menos el dígito final de cada valor es un tallo, el dígito final es la hoja. Los tallos se colocan en una lista vertical, con cada hoja emparejada en un lado. Pueden ser muy útiles para visualizar pequeños conjuntos de datos con no más de dos dígitos significativos. A continuación se muestra un ejemplo. En este ejemplo, multiplicas los tallos por\(10\) y agregas el valor de la hoja para obtener el valor numérico. Así el número máximo de pases de touchdown es\(3 \times 10 + 7 = 37\).
Visualización de tallo y hoja del número de pases de touchdown:
\[\begin{array}{c|c c c c c c c c c c c c c c c } 3 & 2 & 3 & 3 & 7 \\ 2 &0 &0 &1 &1 &1 &2 &2 &2 &3 &8 &8 &9\\ 1 &2 &2 &4 &4 &4 &5 &6 &8 &8 &8 &8 &9 &9\\ 0 &6 &9 \end{array}\]
Paso
Uno de los componentes de una gráfica de caja, el paso es\(1.5\) multiplicar la diferencia entre la bisagra superior y la bisagra inferior.
Muestreo aleatorio estratificado
En el muestreo aleatorio estratificado, la población se divide en varios subgrupos (o estratos). Luego se toman muestras aleatorias de cada subgrupo con tamaños de muestra proporcionales al tamaño del subgrupo en la población. Por ejemplo, si una población contenía igual número de hombres y mujeres, y se sospecha que la variable de interés varía según el género, se podría realizar un muestreo aleatorio estratificado para asegurar una muestra representativa.
Distribución de rango Studentized
La distribución de rango studentized se utiliza para probar la diferencia entre las medias más grandes y más pequeñas. Es similar a la\(t\) distribución que se utiliza cuando sólo hay dos medios.
Regla de Sturgis
Un método para determinar el número de clases para un histograma, la Regla de Sturgis es tomar\(1 + \log _2(N)\) clases, redondeadas al entero más cercano.
Error de suma de cuadrados
En regresión lineal, la suma de cuadrados de error es la suma de errores cuadrados de predicción. En el análisis de varianza, es la suma de las desviaciones cuadradas de las medias celulares para factores entre sujetos y la\(\text{Subjects x Treatment}\) interacción para factores dentro del sujeto.
Distribución simétrica
En una distribución simétrica, las mitades superior e inferior de la distribución son imágenes especulares entre sí. Por ejemplo, en la distribución que se muestra a continuación, las porciones arriba y abajo\(50\) son imágenes especulares entre sí. En una distribución simétrica, la media es igual a la mediana. Antónimo: distribución sesgada.

\(t\)distribución
La\(t\) distribución es la distribución de un valor muestreado a partir de una distribución normal dividida por una estimación de la desviación estándar de la distribución. En la práctica el valor suele ser un estadístico como la media o la diferencia entre medias y la desviación estándar es una estimación del error estándar de la estadística. La\(t\) distribución en leptokúrticos.
\(t\)prueba
Más comúnmente, una prueba de significancia de la diferencia entre medias basada en la distribución t. Otras aplicaciones incluyen
- probar la significancia de la diferencia entre una media muestral y un valor hipotético de la media y
- probar un contraste específico entre medias
Problema de la tercera variable
Un tipo de confusión en el que una tercera variable conduce a una relación causal equivocada entre otras dos. Por ejemplo, las ciudades con mayor número de iglesias tienen un mayor índice delictivo. No obstante, más iglesias no conducen a más delincuencia, sino que la tercera variable, población, lleva tanto a más iglesias como a más delincuencia.
Pase de Touchdown
En el futbol americano, un pase de touchdown ocurre cuando un pase completado da como resultado un touchdown. El pase puede ser a un jugador en la zona de anotación o a un jugador que posteriormente corre hacia la zona de anotación. Un touchdown vale\(6\) puntos y permite una oportunidad en uno (y por algunas reglas dos) punto (s) adicional (s).
Trimean
La trimedia es una medida robusta de tendencia central; es un promedio ponderado de los\(75^{th}\) percentiles\(25^{th}\)\(50^{th}\),, y. Específicamente se calcula de la siguiente manera:
\[\mathrm{Trimean} = 0.25 \times 25^{th} + 0.5 \times 50^{th} + 0.25 \times 75^{th}\]
Puntuación Verdadera
En la teoría clásica de pruebas, la puntuación verdadera es un valor teórico que representa la puntuación de un examinador sin error. Si una persona tomara formas paralelas de una prueba miles de veces (asumiendo que no hay práctica o efectos de fatiga), la media de todas sus puntuaciones sería una buena aproximación de su puntuación verdadera ya que el error sería promediado casi en su totalidad. Debe distinguirse de la validez.
Prueba Tukey HSD
La prueba “Honestamente Significativamente Diferente” (\(HSD\)) desarrollada por el estadístico John Tukey para probar todas las comparaciones por pares entre medias. La prueba se basa en la “distribución de rango studentizado”.
Prueba de dos colas/Probabilidad de dos colas/Prueba no direccional
El último paso en las pruebas de significancia implica calcular la probabilidad de que un estadístico difiera tanto o más del parámetro especificado en la hipótesis nula como lo hacen las estadísticas obtenidas en el experimento.
Una probabilidad calculada considerando diferencias en ambas direcciones (estadística mayor o menor que el parámetro) se denomina probabilidad de dos colas. Por ejemplo, si un parámetro es\(0\) y la estadística es\(12\), una probabilidad de dos colas sería la probabilidad de ser\(≤ -12\) o bien\(≥12\). Compare con la probabilidad de una cola que sería la probabilidad de que un estadístico sea\(≥\) a\(12\) si esa fuera la dirección especificada de antemano.
Error de tipo I
En las pruebas de significancia, el error de rechazar una hipótesis nula verdadera.
Error de tipo II
En las pruebas de significancia, el hecho de no rechazar una hipótesis nula falsa.
Imparcial
Se dice que una muestra es imparcial cuando cada individuo tiene las mismas posibilidades de ser elegido de la población.
Un estimador es imparcial si no sobreestima o subestima sistemáticamente el parámetro que está estimando. Es decir, es imparcial si la media de la distribución muestral del estadístico es el parámetro que está estimando, La media muestral es una estimación imparcial de la media poblacional.
Comparaciones no planificadas/Comparaciones post hoc
Cuando se decide la comparación entre medias después de ver los datos, la comparación se denomina una “comparación no planificada” o una comparación post-hoc. Se requieren diferentes pruebas estadísticas para las comparaciones no planificadas que para las comparaciones planificadas.
Valor superior adyacente
Uno de los componentes de una gráfica de caja, el mayor valor adyacente es el mayor valor en los datos por debajo del\(75^{th}\) percentil.
Bisagra superior
La bisagra superior es uno de los componentes de una gráfica de caja; es el\(75^{th}\) percentil.
Variabilidad/Difusión
La variabilidad se refiere a la medida en que los valores difieren entre sí. Es decir, cuánto varían. La variabilidad también se puede considerar como cuán dispersa está una distribución. La desviación estándar y el rango semiintercuartílico son medidas de variabilidad.
Variable
Algo que pueda tomar diferentes valores. Por ejemplo, diferentes sujetos en un experimento pesan diferentes cantidades. Por lo tanto, el “peso” es una variable en el experimento. O bien, los sujetos pueden recibir diferentes dosis de un medicamento. Esto haría que la “dosis” sea una variable. Las variables pueden ser dependientes o independientes, cualitativas o cuantitativas, y continuas o discretas.
Varianza
La varianza es una medida de variabilidad ampliamente utilizada. Se define como la desviación cuadrática media de las puntuaciones de la media. La fórmula para la varianza calculada en una población entera es
\[\sigma ^2 = \frac{\sum (X-\mu )^2}{N}\]
donde\(σ^2\) representa la varianza,\(μ\) es la media, y\(N\) es el número de puntuaciones.
Cuando se computa en una muestra para estimar la varianza en la población, la población es
\[s^2 = \frac{\sum (X-M)^2}{N-1}\]
donde\(s^2\) está la estimación de varianza,\(M\) es la media muestral, y\(N\) es el número de puntajes en la muestra.
Ley de suma de varianza
La ley de suma de varianza es una expresión para la varianza de la suma de dos variables. Si las variables son independientes y por lo tanto las de Pearson\(r = 0\), la siguiente fórmula representa la varianza de la suma y diferencia de las variables\(X\) y\(Y\):
\[\sigma _{X\pm Y}^{2} = \sigma _{X}^{2} + \sigma _{Y}^{2}\]
Tenga en cuenta que agrega las varianzas para ambos\(X + Y\) y\(X - Y\).
Si\(X\) y\(Y\) están correlacionados, entonces se debe usar la siguiente fórmula (que el primero es un caso especial):
\[\sigma _{X\pm Y}^{2} = \sigma _{X}^{2} + \sigma _{Y}^{2} \pm 2\rho \sigma _X \sigma _Y\]
donde\(ρ\) está el valor poblacional de la correlación. En una muestra\(r\) se utiliza como estimación de\(ρ\).
Diseño dentro de las asignaturas
Un diseño experimental en el que la variable independiente es una variable dentro de los sujetos.
Factor dentro de los sujetos/Variable dentro de los sujetos/Factor de medidas repetidas/Variable de medidas repetidas
Una variable dentro de los sujetos es una variable independiente que se manipula probando cada sujeto en cada nivel de la variable. Comparar con una variable entre sujetos en la que se utilizan diferentes grupos de sujetos para cada nivel de la variable.
Intercepción en Y
La\(Y\) -intercepción de una línea es el valor de\(Y\) en el punto en el que la línea intercepta el\(Y\) eje. Es el valor de\(Y\) cuando\(X\) es igual\(0\). El\(Y\) intercepto de la línea negra que se muestra en la gráfica es\(0.785\).
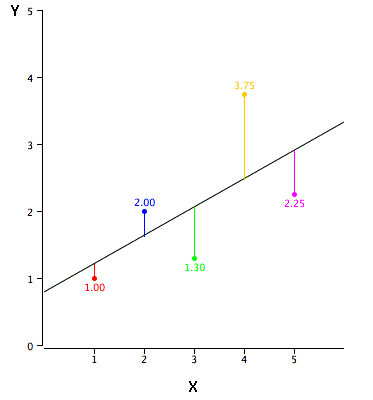
\(Z\)puntuación/Puntuación estándar/Estandarizar /Desviación normal estándar
El número de desviaciones estándar una puntuación es de la media de su población. El término “puntaje estándar” se usa generalmente para poblaciones normales; los términos "\(Z\)puntuación” y “desviación normal” solo deben usarse en referencia a distribuciones normales. La transformación de una puntuación en bruto\(X\) a una\(Z\) puntuación se puede hacer usando la siguiente fórmula:
\[Z = \frac{X-\mu }{\sigma }\]
Transformar una variable de esta manera se llama “estandarizar” la variable. Se debe tener en cuenta que si no\(X\) se distribuye normalmente entonces la variable transformada tampoco se distribuirá normalmente.


