1.3: Datos, Muestreo y Variación en Datos y Muestreo
- Page ID
- 153442
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Los datos pueden provenir de una población o de una muestra. Las letras minúsculas como\(x\) o\(y\) generalmente se utilizan para representar valores de datos. La mayoría de los datos se pueden poner en las siguientes categorías:
- Cualitativo
- Cuantitativo
Los datos cualitativos son el resultado de categorizar o describir atributos de una población. El color del cabello, el tipo de sangre, el grupo étnico, el automóvil que conduce una persona y la calle en la que vive son ejemplos de datos cualitativos. Los datos cualitativos generalmente se describen con palabras o letras. Por ejemplo, el color del cabello puede ser negro, marrón oscuro, marrón claro, rubio, gris o rojo. El tipo de sangre puede ser AB+, O- o B+. Los investigadores suelen preferir utilizar datos cuantitativos sobre datos cualitativos porque se presta más fácilmente al análisis matemático. Por ejemplo, no tiene sentido encontrar un color de pelo promedio o un tipo de sangre.
Los datos cuantitativos son siempre números. Los datos cuantitativos son el resultado de contar o medir atributos de una población. La cantidad de dinero, la frecuencia del pulso, el peso, el número de personas que viven en tu pueblo y el número de estudiantes que toman estadísticas son ejemplos de datos cuantitativos. Los datos cuantitativos pueden ser discretos o continuos.
Todos los datos que son el resultado del conteo se denominan datos discretos cuantitativos. Estos datos toman solo ciertos valores numéricos. Si cuentas el número de llamadas telefónicas que recibes por cada día de la semana, podrías obtener valores como cero, uno, dos o tres.
Todos los datos que son el resultado de la medición son datos cuantitativos continuos asumiendo que podemos medir con precisión. Medir ángulos en radianes podría dar como resultado números tales como\(\frac{\pi}{6}\),\(\frac{\pi}{3}\),\(\frac{\pi}{2}\),\(\pi\),\(\frac{3\pi}{4}\),, y así sucesivamente. Si tú y tus amigos llevan mochilas con libros en ellos a la escuela, los números de libros en las mochilas son datos discretos y los pesos de las mochilas son datos continuos.
Muestra de datos discretos cuantitativos
Los datos son la cantidad de libros que los alumnos llevan en sus mochilas. Muestreas a cinco alumnos. Dos estudiantes llevan tres libros, un estudiante lleva cuatro libros, un estudiante lleva dos libros y un estudiante lleva un libro. Los números de libros (tres, cuatro, dos y uno) son los datos discretos cuantitativos.
Ejercicio\(\PageIndex{1}\)
Los datos son el número de máquinas en un gimnasio. Muestreas cinco gimnasios. Un gimnasio tiene 12 máquinas, un gimnasio tiene 15 máquinas, un gimnasio tiene diez máquinas, un gimnasio tiene 22 máquinas y el otro gimnasio tiene 20 máquinas. ¿Qué tipo de datos son estos?
- Contestar
-
datos discretos cuantitativos
Muestra de Datos Continuos Cuantitativos
Los datos son los pesos de mochilas con libros en ellas. Muestrea los mismos cinco alumnos. Los pesos (en libras) de sus mochilas son 6.2, 7, 6.8, 9.1, 4.3. Observe que las mochilas que llevan tres libros pueden tener diferentes pesos. Los pesos son datos cuantitativos continuos porque se miden los pesos.
Ejercicio\(\PageIndex{2}\)
Los datos son las áreas de césped en pies cuadrados. Muestreas cinco casas. Las áreas de césped son 144 pies cuadrados, 160 pies cuadrados, 190 pies cuadrados, 180 pies cuadrados y 210 pies cuadrados. ¿Qué tipo de datos son estos?
- Contestar
-
datos cuantitativos continuos
Ejercicio\(\PageIndex{3}\)
Usted va al supermercado y compra tres latas de sopa (19 onzas) de bisque de tomate, 14.1 onzas de lentejas, y 19 onzas boda italiana), dos paquetes de frutos secos (nueces y cacahuetes), cuatro tipos diferentes de vegetales (brócoli, coliflor, espinacas y zanahorias), y dos postres (16 onzas de helado Cherry Garcia y dos libras (32 onzas de galletas con chispas de chocolate).
Nombra conjuntos de datos que sean cuantitativos discretos, cuantitativos continuos y cualitativos.
Solución
Una posible solución:
- Las tres latas de sopa, dos paquetes de frutos secos, cuatro tipos de verduras y dos postres son datos discretos cuantitativos porque los cuentas.
- Los pesos de las sopas (19 onzas, 14.1 onzas, 19 onzas) son datos cuantitativos continuos porque se miden los pesos con la mayor precisión posible.
- Tipos de sopas, frutos secos, verduras y postres son datos cualitativos porque son categóricos.
Intente identificar conjuntos de datos adicionales en este ejemplo.
Muestra de datos cualitativos
Los datos son los colores de las mochilas. Nuevamente, muestras a los mismos cinco alumnos. Un estudiante tiene una mochila roja, dos estudiantes tienen mochilas negras, un estudiante tiene una mochila verde y un estudiante tiene una mochila gris. Los colores rojo, negro, negro, verde y gris son datos cualitativos.
Ejercicio\(\PageIndex{4}\)
Los datos son los colores de las casas. Muestreas cinco casas. Los colores de las casas son blanco, amarillo, blanco, rojo y blanco. ¿Qué tipo de datos son estos?
- Contestar
-
datos cualitativos
Ejercicio Colaborativo\(\PageIndex{1}\)
Trabajar en colaboración para determinar el tipo de datos correcto (cuantitativo o cualitativo). Indicar si los datos cuantitativos son continuos o discretos. Pista: Los datos que son discretos a menudo comienzan con las palabras “el número de”.
- el número de pares de zapatos que tienes
- el tipo de auto que conduces
- donde vas de vacaciones
- la distancia que está de tu casa a la tienda de abarrotes más cercana
- el número de clases que tomas por año escolar.
- la matrícula para tus clases
- el tipo de calculadora que usas
- calificaciones de películas
- preferencias de partidos políticos
- pesos de luchadores de sumo
- cantidad de dinero (en dólares) ganada jugando al poker
- número de respuestas correctas en un cuestionario
- actitudes de los pueblos hacia el gobierno
- Puntajes de coeficiente intelectual (Esto puede causar cierta discusión).
Los ítems a, e, f, k y l son discretos cuantitativos; los ítems d, j y n son continuos cuantitativos; los ítems b, c, g, h, i y m son cualitativos.
Ejercicio\(\PageIndex{5}\)
Determinar el tipo de datos correcto (cuantitativo o cualitativo) para el número de autos en un estacionamiento. Indicar si los datos cuantitativos son continuos o discretos.
- Contestar
-
cuantitativo discreto
Ejercicio\(\PageIndex{6}\)
Un profesor de estadística recopila información sobre la clasificación de sus alumnos como estudiantes de primer año, segundo año, juniors o seniors. Los datos que recoge se resumen en el gráfico circular Figura\(\PageIndex{1}\). ¿Qué tipo de datos muestra esta gráfica?
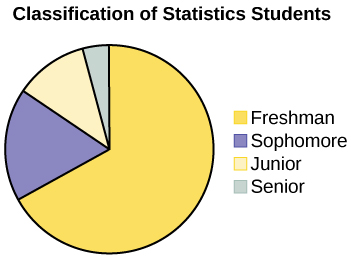
- Contestar
-
Este gráfico circular muestra a los alumnos de cada año, que son datos cualitativos.
Ejercicio\(\PageIndex{7}\)
El registrador de la Universidad Estatal mantiene registros del número de horas de crédito que los estudiantes completan cada semestre. Los datos que recoge se resumen en el histograma. Los límites de clase son de 10 a menos de 13, de 13 a menos de 16, de 16 a menos de 19, de 19 a menos de 22 y de 22 a menos de 25.
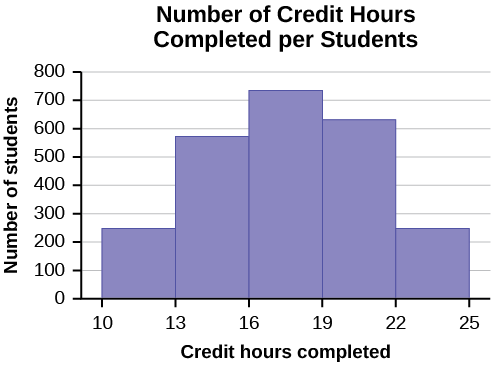
¿Qué tipo de datos muestra esta gráfica?
- Contestar
-
Se utiliza un histograma para mostrar datos cuantitativos: los números de horas de crédito completadas. Debido a que los estudiantes solo pueden completar un número entero de horas (no se permiten fracciones de horas), estos datos son discretos cuantitativos.
Discusión de datos cualitativos
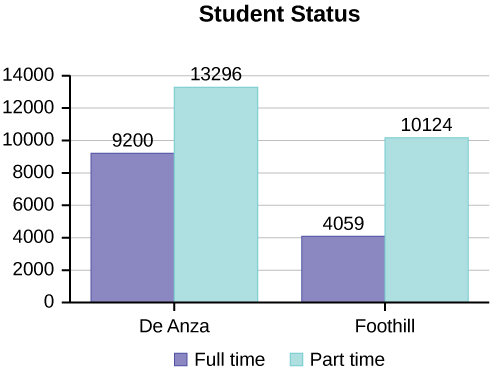
A continuación se muestran tablas que comparan el número de estudiantes de medio tiempo y tiempo completo en De Anza College y Foothill College matriculados para el trimestre de primavera de 2010. Las tablas muestran recuentos (frecuencias) y porcentajes o proporciones (frecuencias relativas). Las columnas porcentuales facilitan la comparación de las mismas categorías en los colegios. Visualizar porcentajes junto con los números suele ser útil, pero es particularmente importante a la hora de comparar conjuntos de datos que no tienen los mismos totales, como el total de inscripciones para ambas universidades en este ejemplo. Observe cuánto mayor es el porcentaje para estudiantes de medio tiempo en Foothill College en comparación con De Anza College.
| Colegio De Anza | Colegio Foothill | |||||
|---|---|---|---|---|---|---|
| Número | Por ciento | Número | Por ciento | |||
| Tiempo completo | 9,200 | 40.9% | Tiempo completo | 4,059 | 28.6% | |
| Medio tiempo | 13,296 | 59.1% | Medio tiempo | 10,124 | 71.4% | |
| Total | 22,496 | 100% | Total | 14,183 | 100% | |
Las tablas son una buena manera de organizar y mostrar datos. Pero los gráficos pueden ser aún más útiles para comprender los datos. No existen reglas estrictas sobre qué gráficas usar. Dos gráficas que se utilizan para mostrar datos cualitativos son los gráficos circulares y los gráficos de barras.
- En un gráfico circular, las categorías de datos están representadas por cuñas en un círculo y son proporcionales en tamaño al porcentaje de individuos en cada categoría.
- En una gráfica de barras, la longitud de la barra para cada categoría es proporcional al número o porcentaje de individuos en cada categoría. Las barras pueden ser verticales u horizontales.
- Un gráfico de Pareto consta de barras que se ordenan en orden por tamaño de categoría (de mayor a menor).
Mire Figuras\(\PageIndex{3}\)\(\PageIndex{4}\) y determine qué gráfico (pastel o barra) cree que muestra mejor las comparaciones.
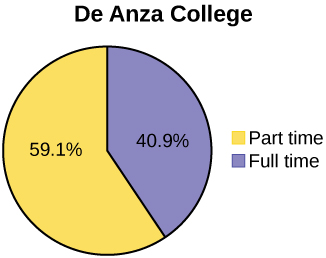
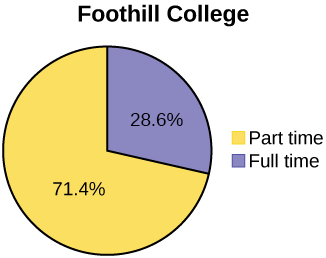
Es una buena idea mirar una variedad de gráficas para ver cuál es la más útil para mostrar los datos. Podríamos tomar diferentes decisiones de lo que creemos que es el “mejor” gráfico dependiendo de los datos y el contexto. Nuestra elección también depende de para qué estamos utilizando los datos.
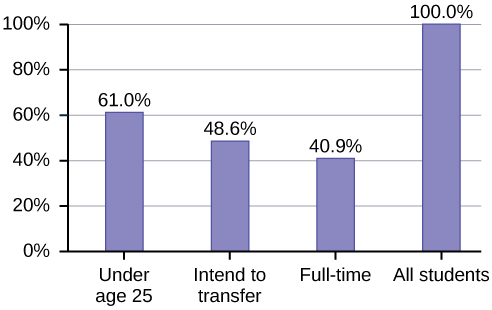
Porcentajes que se suman a más (o menos) de 100%
En ocasiones los porcentajes suman ser más del 100% (o menos del 100%). En la gráfica, los porcentajes se suman a más del 100% porque los estudiantes pueden estar en más de una categoría. Un gráfico de barras es apropiado para comparar el tamaño relativo de las categorías. No se puede utilizar un gráfico circular. Tampoco se podría utilizar si los porcentajes se sumaron a menos del 100%.
| Característico/Categoría | Por ciento |
|---|---|
| Estudiantes de Tiempo Completo | 40.9% |
| Alumnos que pretendan trasladarse a una institución educativa de 4 años | 48.6% |
| Estudiantes menores de 25 años | 61.0% |
| TOTAL | 150.5% |
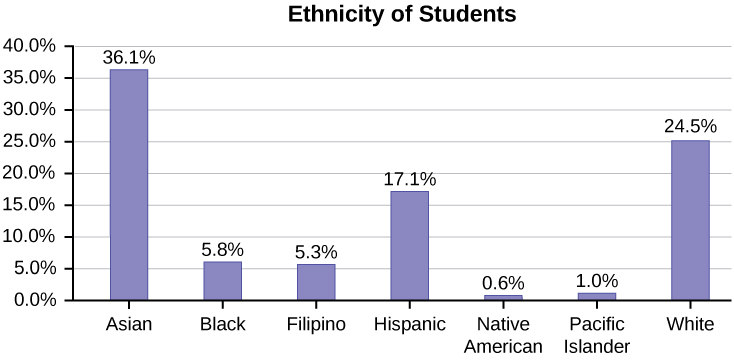
Omitir categorías/Datos faltantes
La tabla muestra Etnicidad de los estudiantes pero falta la categoría “Otros/Desconocido”. Esta categoría contiene personas que no sintieron que encajaban en ninguna de las categorías de etnia o que se negaron a responder. Observe que las frecuencias no suman el número total de alumnos. En esta situación, cree un gráfico de barras y no un gráfico circular.
| Frecuencia | Por ciento | |
|---|---|---|
| Asiático | 8,794 | 36.1% |
| Negro | 1,412 | 5.8% |
| Filipino | 1,298 | 5.3% |
| Hispano | 4,180 | 17.1% |
| Nativo americano | 146 | 0.6% |
| Isleños del Pacífico | 236 | 1.0% |
| Blanco | 5,978 | 24.5% |
| TOTAL | 22,044 de 24,382 | 90.4% de 100% |
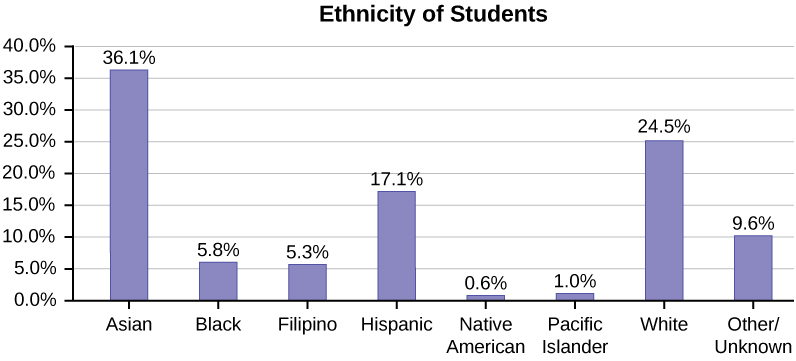
La siguiente gráfica es la misma que la gráfica anterior pero se ha incluido el porcentaje “Otros/Desconocido” (9.6%). La categoría “Otros/Desconocidos” es grande en comparación con algunas de las otras categorías (Nativo Americano, 0.6%, Isleño del Pacífico 1.0%). Esto es importante saber cuando pensamos en lo que nos están diciendo los datos.
Este gráfico de barras en particular en la Figura\(\PageIndex{4}\) puede ser difícil de entender visualmente. La gráfica de la Figura\(\PageIndex{5}\) es una gráfica de Pareto. El gráfico de Pareto tiene las barras ordenadas de mayor a menor y es más fácil de leer e interpretar.
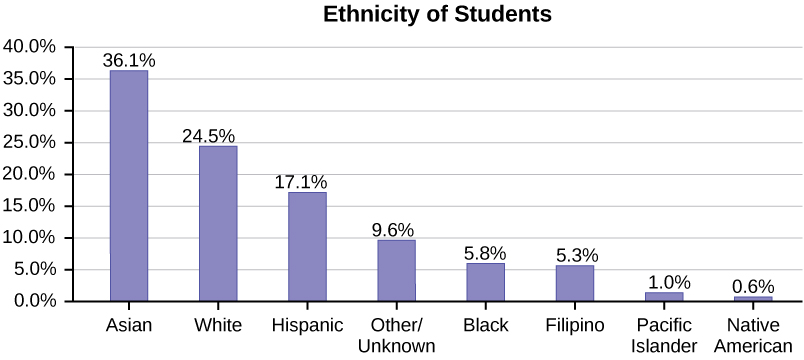
Gráficos circulares: No faltan datos
Los siguientes gráficos circulares tienen incluida la categoría “Otros/Desconocidos” (ya que los porcentajes deben sumarse al 100%). El gráfico de la Figura\(\PageIndex{6}\) está organizado por el tamaño de cada cuña, lo que la convierte en una gráfica más visualmente informativa que la gráfica alfabética sin clasificar de la Figura\(\PageIndex{6}\).
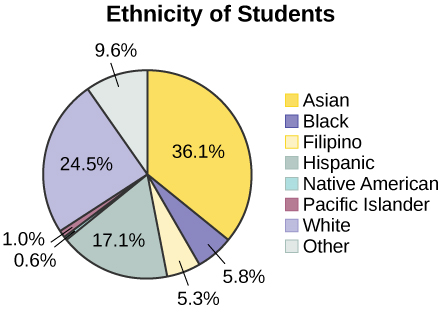
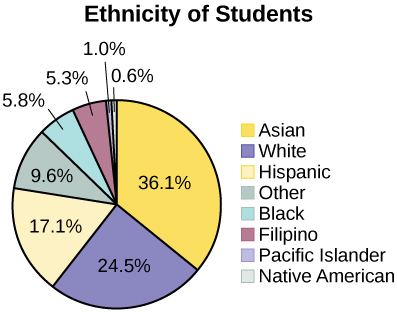
Muestreo
Recopilar información sobre toda una población a menudo cuesta demasiado o es prácticamente imposible. En cambio, utilizamos una muestra de la población. Una muestra debe tener las mismas características que la población que representa. La mayoría de los estadísticos utilizan diversos métodos de muestreo aleatorio en un intento de lograr este objetivo. En esta sección se describirán algunos de los métodos más comunes. Existen varios métodos diferentes de muestreo aleatorio. En cada forma de muestreo aleatorio, cada miembro de una población inicialmente tiene las mismas posibilidades de ser seleccionado para la muestra. Cada método tiene pros y contras. El método más fácil de describir se llama una muestra aleatoria simple. Cualquier grupo de n individuos es igualmente probable que sea elegido por cualquier otro grupo de n individuos si se utiliza la técnica de muestreo aleatorio simple. Es decir, cada muestra del mismo tamaño tiene las mismas posibilidades de ser seleccionada. Por ejemplo, supongamos que Lisa quiere formar un grupo de estudio de cuatro personas (ella misma y otras tres personas) a partir de su clase de pre-cálculo, que tiene 31 miembros sin incluir a Lisa. Para elegir una simple muestra aleatoria de talla tres de los otros miembros de su clase, Lisa podría poner los 31 nombres en un sombrero, sacudir el sombrero, cerrar los ojos y elegir tres nombres. Una forma más tecnológica es que Lisa enumere primero los apellidos de los integrantes de su clase junto con un número de dos dígitos, como en la Tabla\(\PageIndex{2}\):
| ID | Nombre | ID | Nombre | ID | Nombre |
|---|---|---|---|---|---|
| 00 | Anselmo | 11 | King | 21 | Roquero |
| 01 | Bautista | 12 | Legeny | 22 | Roth |
| 02 | Bayani | 13 | Lundquist | 23 | Rowell |
| 03 | Cheng | 14 | Macierz | 24 | Salangsang |
| 04 | Cuarismo | 15 | Motogawa | 25 | Slade |
| 05 | Cuningham | 16 | Okimoto | 26 | Stratcher |
| 06 | Fontecha | 17 | Patel | 27 | Tallai |
| 07 | Hong | 18 | Precio | 28 | Tran |
| 08 | Hoobler | 19 | Quizon | 29 | Wai |
| 09 | Jiao | 20 | Reyes | 30 | Madera |
| 10 | Khan |
Lisa puede usar una tabla de números aleatorios (que se encuentran en muchos libros de estadísticas y manuales matemáticos), una calculadora o una computadora para generar números aleatorios. Para este ejemplo, supongamos que Lisa elige generar números aleatorios a partir de una calculadora. Los números generados son los siguientes:
0.94360; 0.99832; 0.14669; 0.51470; 0.40581; 0.73381; 0.04399
Lisa lee grupos de dos dígitos hasta que ha elegido a tres miembros de la clase (es decir, lee 0.94360 como los grupos 94, 43, 36, 60). Cada número aleatorio solo puede aportar un miembro de la clase. De ser necesario, Lisa podría haber generado más números aleatorios.
Los números aleatorios 0.94360 y 0.99832 no contienen números apropiados de dos dígitos. Sin embargo, el tercer número aleatorio, 0.14669, contiene 14 (el cuarto número aleatorio también contiene 14), el quinto número aleatorio contiene 05 y el séptimo número aleatorio contiene 04. El número de dos dígitos 14 corresponde a Macierz, 05 corresponde a Cuningham, y 04 corresponde al cuarismo. Además de ella, el grupo de Lisa estará formado por Marcierz, Cuningham y Cuarismo.
Para generar números aleatorios:
- Presione MATH.
- Flecha sobre PRB.
- Prensa 5:Randint (. Entrar 0, 30).
- Presione ENTRAR para el primer número aleatorio.
- Presione ENTRAR dos veces más para los otros 2 números aleatorios. Si hay una repetición, presione ENTRAR nuevamente.
Nota: RandInt (0, 30, 3) generará 3 números aleatorios.
Además del muestreo aleatorio simple, existen otras formas de muestreo que implican un proceso casual para obtener la muestra. Otros métodos de muestreo aleatorio bien conocidos son la muestra estratificada, la muestra agrupada y la muestra sistemática.
Para elegir una muestra estratificada, dividir la población en grupos llamados estratos y luego tomar un número proporcional de cada estrato. Por ejemplo, podrías estratificar (agrupar) tu población universitaria por departamento y luego elegir una muestra aleatoria simple proporcionada de cada estrato (cada departamento) para obtener una muestra aleatoria estratificada. Para elegir una muestra aleatoria simple de cada departamento, numerar a cada miembro del primer departamento, numerar a cada miembro del segundo departamento y hacer lo mismo para los departamentos restantes. Luego use muestreo aleatorio simple para elegir números proporcionales del primer departamento y hacer lo mismo para cada uno de los departamentos restantes. Esos números escogidos del primer departamento, escogidos del segundo departamento, y así sucesivamente representan a los integrantes que conforman la muestra estratificada.
Para elegir una muestra de conglomerados, divida la población en clusters (grupos) y luego seleccionar aleatoriamente algunos de los clusters. Todos los miembros de estos clústeres están en la muestra del clúster. Por ejemplo, si muestreas aleatoriamente cuatro departamentos de tu población universitaria, los cuatro departamentos conforman la muestra del clúster. Divide tu facultad universitaria por departamento. Los departamentos son los clusters. Numere cada departamento y luego elija cuatro números diferentes usando muestreo aleatorio simple. Todos los miembros de los cuatro departamentos con esos números son la muestra del clúster.
Para elegir una muestra sistemática, seleccionar aleatoriamente un punto de partida y tomar cada n º dato de un listado de la población. Por ejemplo, supongamos que tienes que hacer una encuesta telefónica. Tu agenda telefónica contiene 20,000 anuncios de residencia. Debe elegir 400 nombres para la muestra. Numere la población entre 1 y 20,000 y luego use una muestra aleatoria simple para elegir un número que represente el nombre de la muestra. Luego elige cada quincuagésimo nombre a partir de entonces hasta que tengas un total de 400 nombres (es posible que tengas que volver al comienzo de tu lista telefónica). El muestreo sistemático se elige frecuentemente porque es un método sencillo.
Un tipo de muestreo no aleatorio es el muestreo de conveniencia. El muestreo de conveniencia implica el uso de resultados que están fácilmente disponibles. Por ejemplo, una tienda de software informático realiza un estudio de marketing entrevistando a clientes potenciales que pasan a estar en la tienda navegando a través del software disponible. Los resultados del muestreo por conveniencia pueden ser muy buenos en algunos casos y altamente sesgados (favorecen ciertos resultados) en otros.
Los datos de muestreo deben hacerse con mucho cuidado. Recopilar datos descuidadamente puede tener resultados devastadores. Las encuestas enviadas por correo a los hogares y luego devueltas pueden ser muy sesgadas (pueden favorecer a cierto grupo). Es mejor que la persona que realiza la encuesta seleccione a los encuestados de la muestra.
El muestreo aleatorio verdadero se realiza con reemplazo. Es decir, una vez que se elige a un miembro, ese miembro regresa a la población y así puede ser elegido más de una vez. Sin embargo, por razones prácticas, en la mayoría de las poblaciones, el muestreo aleatorio simple se realiza sin reemplazo. Por lo general, las encuestas se realizan sin reemplazo. Es decir, un miembro de la población podrá ser elegido sólo una vez. La mayoría de las muestras se toman de poblaciones grandes y la muestra tiende a ser pequeña en comparación con la población. Dado que este es el caso, el muestreo sin reemplazo es aproximadamente lo mismo que el muestreo con reemplazo porque la posibilidad de recoger al mismo individuo más de una vez con reemplazo es muy baja.
En una población universitaria de 10,000 personas, supongamos que desea elegir una muestra de 1,000 al azar para una encuesta. Para cualquier muestra particular de 1,000, si está muestreando con reemplazo,
- la probabilidad de elegir a la primera persona es 1,000 de 10,000 (0.1000);
- la probabilidad de elegir una segunda persona diferente para esta muestra es 999 de 10,000 (0.0999);
- la posibilidad de volver a recoger a la misma persona es 1 de cada 10,000 (muy baja).
Si está muestreando sin reemplazo,
- la probabilidad de recoger a la primera persona para cualquier muestra en particular es 1000 de 10,000 (0.1000);
- la probabilidad de elegir una segunda persona diferente es 999 de 9,999 (0.0999);
- no reemplaces a la primera persona antes de elegir a la siguiente persona.
Compara las fracciones 999/10,000 y 999/9,999. Para mayor precisión, lleve las respuestas decimales a cuatro decimales. A cuatro decimales, estos números son equivalentes (0.0999).
El muestreo sin reemplazo en lugar de muestreo con reemplazo se convierte en un problema matemático solo cuando la población es pequeña. Por ejemplo, si la población es de 25 personas, la muestra es de diez, y estás muestreando con reemplazo para cualquier muestra en particular, entonces la probabilidad de recoger a la primera persona es de diez de 25, y la probabilidad de elegir una segunda persona diferente es de nueve de 25 (se reemplaza a la primera persona).
Si realiza una muestra sin reemplazo, entonces la probabilidad de elegir a la primera persona es de diez de 25, y luego la posibilidad de elegir a la segunda persona (que es diferente) es de nueve de cada 24 (no reemplaza a la primera persona).
Compara las fracciones 9/25 y 9/24. A cuatro decimales, 9/25 = 0.3600 y 9/24 = 0.3750. A cuatro decimales, estos números no son equivalentes.
Al analizar los datos, es importante estar al tanto de los errores de muestreo y de no muestreo. El proceso real de muestreo provoca errores de muestreo. Por ejemplo, la muestra puede no ser lo suficientemente grande. Los factores no relacionados con el proceso de muestreo provocan errores de no muestreo. Un dispositivo de conteo defectuoso puede causar un error de no muestreo.
En realidad, una muestra nunca será exactamente representativa de la población por lo que siempre habrá algún error de muestreo. Como regla general, cuanto mayor es la muestra, menor es el error de muestreo.
En las estadísticas, se crea un sesgo de muestreo cuando se recolecta una muestra de una población y algunos miembros de la población no son tan propensos a ser elegidos como otros (recuerde, cada miembro de la población debe tener la misma probabilidad de ser elegido). Cuando ocurre un sesgo de muestreo, puede haber conclusiones incorrectas sobre la población que se está estudiando.
Ejercicio\(\PageIndex{8}\)
Se realiza un estudio para determinar la matrícula promedio que pagan los estudiantes de pregrado del estado de San José por semestre. A cada alumno de las siguientes muestras se le pregunta cuánta matrícula pagó para el semestre de otoño. ¿Cuál es el tipo de muestreo en cada caso?
- Se toma una muestra de 100 estudiantes de pregrado del estado de San José organizando los nombres de los estudiantes por clasificación (primer año, segundo año, junior o senior), y luego seleccionando 25 estudiantes de cada uno.
- Se utiliza un generador de números aleatorios para seleccionar a un estudiante del listado alfabético de todos los estudiantes de pregrado en el semestre de otoño. A partir de ese alumno, se elige a cada estudiante 50 hasta que se incluyen 75 alumnos en la muestra.
- Se utiliza un método completamente aleatorio para seleccionar a 75 alumnos. Cada estudiante de licenciatura en el semestre de otoño tiene la misma probabilidad de ser elegido en cualquier etapa del proceso de muestreo.
- Los estudiantes de primer año, segundo, junior y senior están numerados uno, dos, tres y cuatro, respectivamente. Se utiliza un generador de números aleatorios para elegir dos de esos años. Todos los alumnos en esos dos años están en la muestra.
- Se pide a un auxiliar administrativo que se pare frente a la biblioteca un miércoles y que pregunte a los primeros 100 estudiantes de pregrado que encuentre lo que pagaron por la matrícula el semestre de otoño. Esos 100 alumnos son la muestra.
Contestar
a. estratificado; b. sistemático; c. simple aleatorio; d. cúmulo; e. conveniencia
Ejemplo\(\PageIndex{9}\): Calculator
Vas a utilizar el generador de números aleatorios para generar diferentes tipos de muestras a partir de los datos. Esta tabla muestra seis conjuntos de puntajes de cuestionarios (cada cuestionario cuenta 10 puntos) para una clase de estadística elemental.
| #1 | #2 | #3 | #4 | #5 | #6 |
|---|---|---|---|---|---|
| 5 | 7 | 10 | 9 | 8 | 3 |
| 10 | 5 | 9 | 8 | 7 | 6 |
| 9 | 10 | 8 | 6 | 7 | 9 |
| 9 | 10 | 10 | 9 | 8 | 9 |
| 7 | 8 | 9 | 5 | 7 | 4 |
| 9 | 9 | 9 | 10 | 8 | 7 |
| 7 | 7 | 10 | 9 | 8 | 8 |
| 8 | 8 | 9 | 10 | 8 | 8 |
| 9 | 7 | 8 | 7 | 7 | 8 |
| 8 | 8 | 10 | 9 | 8 | 7 |
Instrucciones: Utilice el Generador de Números Aleatorios para recoger muestras.
- Crear una muestra estratificada por columna. Elige tres puntuaciones de prueba al azar de cada columna.
- Numere cada fila del uno al diez.
- En tu calculadora, presiona Matemáticas y haz la flecha hacia PRB.
- Para la columna 1, Presione 5:Randint (e ingrese 1,10). Presione ENTER. Registrar el número. Presiona ENTRAR 2 veces más (incluso las repeticiones). Registre estos números. Registre las tres puntuaciones de los cuestionarios en la columna uno que correspondan a estos tres números.
- Repita para las columnas dos a seis.
- Estas 18 puntuaciones de los cuestionarios son una muestra estratificada.
- Cree una muestra de clúster seleccionando dos de las columnas. Utilice los números de columna: uno a seis.
- Presione MATH y flecha hacia PRB.
- Presione 5:Randint (e ingrese 1,6). Presione ENTER. Registrar el número. Presione ENTRAR y registre ese número.
- Los dos números son para dos de las columnas.
- Las puntuaciones de los cuestionarios (20 de ellas) en estas 2 columnas son la muestra del clúster.
- Crea una muestra aleatoria simple de 15 puntajes de quiz.
- Utilice la numeración del uno al 60.
- Presione MATH. Flecha sobre PRB. Presione 5:Randint (e ingrese 1, 60).
- Presione ENTRAR 15 veces y registre los números.
- Registre las puntuaciones del cuestionario que correspondan a estos números.
- Estas 15 puntuaciones de quiz son la muestra sistemática.
- Crear una muestra sistemática de 12 puntajes de cuestionarios.
- Utilice la numeración del uno al 60.
- Presione MATH. Flecha sobre PRB. Presione 5:Randint (e ingrese 1, 60).
- Presione ENTER. Registre el número y la puntuación del primer cuestionario. A partir de ese número, cuente diez puntajes del cuestionario y registre esa puntuación del cuestionario. Siga contando diez puntajes de cuestionarios y grabando la puntuación del cuestionario hasta que tenga una muestra de 12 puntajes del cuestionario. Puedes envolverte (volver al principio).
Ejemplo\(\PageIndex{10}\)
Determinar el tipo de muestreo utilizado (simple aleatorio, estratificado, sistemático, conglomerado o conveniencia).
- Un entrenador de futbol selecciona a seis jugadores de un grupo de chicos de ocho a diez años, siete jugadores de un grupo de chicos de 11 a 12 años, y tres jugadores de un grupo de chicos de 13 a 14 años para formar un equipo de futbol recreativo.
- Un encuestador entrevista a todo el personal de recursos humanos en cinco empresas diferentes de alta tecnología.
- Un investigador educativo de secundaria entrevista a 50 profesoras de secundaria y 50 profesores varones de secundaria.
- Un investigador médico entrevista a cada tres pacientes oncológicos de una lista de pacientes oncológicos en un hospital local.
- Un consejero de secundaria utiliza una computadora para generar 50 números aleatorios y luego elige a los estudiantes cuyos nombres corresponden a los números.
- Un alumno entrevista a compañeros de clase en su clase de álgebra para determinar cuántos pares de jeans posee un estudiante, en promedio.
Contestar
a. estratificado; b. cúmulo; c. estratificado; d. sistemático; e. simple aleatorio; f.conveniencia
Ejercicio\(\PageIndex{11}\)
Determinar el tipo de muestreo utilizado (simple aleatorio, estratificado, sistemático, conglomerado o conveniencia).
Un director de secundaria sondea a 50 estudiantes de primer año, 50 estudiantes de segundo año, 50 juniors y 50 seniors con respecto a cambios de políticas para actividades extraescolares.
Contestar
estratificado
Si examináramos dos muestras que representan la misma población, aunque usáramos métodos de muestreo aleatorio para las muestras, no serían exactamente las mismas. Así como hay variación en los datos, hay variación en las muestras. A medida que te acostumbres al muestreo, la variabilidad comenzará a parecer natural.
Ejemplo\(\PageIndex{12}\): Sampling
Supongamos que ABC College tiene 10,000 estudiantes de medio tiempo (la población). Nos interesa la cantidad promedio de dinero que un estudiante de medio tiempo gasta en libros en el trimestre de otoño. Preguntar a los 10 mil alumnos es una tarea casi imposible. Supongamos que tomamos dos muestras diferentes.
Primero, utilizamos muestreo de conveniencia y encuestamos a diez estudiantes de una clase de química orgánica de primer trimestre. Muchos de estos estudiantes están tomando cálculo de primer trimestre además de la clase de química orgánica. La cantidad de dinero que gastan en libros es la siguiente:
$128; $87; $173; $116; $130; $204; $147; $189; $93; $153
La segunda muestra se toma utilizando una lista de personas mayores que toman clases de P.E. y que toman cada cinco personas mayores de la lista, para un total de diez personas mayores. Gastan:
$50; $40; $36; $15; $50; $100; $40; $53; $22; $22
a. ¿Cree que alguna de estas muestras es representativa de (o es característica de) la totalidad de la población estudiantil de 10 mil tiempo parcial?
Contestar
a. No. La primera muestra probablemente está formada por estudiantes orientados a la ciencia. Además del curso de química, algunos de ellos también están tomando cálculo de primer trimestre. Los libros para estas clases suelen ser caros. La mayoría de estos estudiantes están, más que probablemente, pagando más que el estudiante medio de medio tiempo por sus libros. La segunda muestra es un grupo de personas mayores que están, más que probablemente, tomando cursos de salud e interés. La cantidad de dinero que gastan en libros es probablemente mucho menor que el estudiante promedio a tiempo parcial. Ambas muestras están sesgadas. Además, en ambos casos, no todos los alumnos tienen la posibilidad de estar en ninguna de las muestras.
b. Dado que estas muestras no son representativas de toda la población, ¿es prudente utilizar los resultados para describir a toda la población?
Contestar
b. No. Para estas muestras, cada miembro de la población no tuvo una probabilidad igual de probable de ser elegido.
Ahora, supongamos que tomamos una tercera muestra. Elegimos diez estudiantes de medio tiempo diferentes de las disciplinas de química, matemáticas, inglés, psicología, sociología, historia, enfermería, educación física, arte y desarrollo de la primera infancia. (Suponemos que estas son las únicas disciplinas en las que están matriculados los estudiantes de medio tiempo en ABC College y que en cada una de las disciplinas se inscriben un número igual de alumnos de medio tiempo). Cada alumno es elegido mediante muestreo aleatorio simple. Usando una calculadora, se generan números aleatorios y se selecciona a un estudiante de una disciplina en particular si tiene un número correspondiente. Los alumnos gastan las siguientes cantidades:
$180; $50; $150; $85; $260; $75; $180; $200; $200; $150
c. ¿La muestra está sesgada?
Contestar
Los estudiantes suelen preguntar si es “lo suficientemente bueno” tomar una muestra, en lugar de encuestar a toda la población. Si la encuesta se hace bien, la respuesta es sí.
Ejercicio\(\PageIndex{12}\)
Una estación de radio local tiene una base de fans de 20,000 oyentes. La emisora quiere saber si su público preferiría más música o más programas de entrevistas. Preguntar a los 20 mil oyentes es una tarea casi imposible.
La estación utiliza muestreo de conveniencia y encuesta a las primeras 200 personas que conocen en uno de los eventos de conciertos musicales de la estación. 24 personas dijeron que preferirían más programas de entrevistas, y 176 personas dijeron que preferirían más música.
¿Cree que esta muestra es representativa de (o es característica de) toda la población de 20 mil oyentes?
Contestar
La muestra probablemente consiste más en personas que prefieren la música porque es un evento de concierto. Además, la muestra representa sólo a quienes se presentaron al evento antes que la mayoría. La muestra probablemente no representa a toda la base de fans y probablemente esté sesgada hacia las personas que preferirían la música.
Ejercicio Colaborativo\(\PageIndex{8}\)
Como clase, determine si las siguientes muestras son representativas o no. Si no lo son, discuta las razones.
- Para encontrar el promedio de promedio de todos los estudiantes de una universidad, use como muestra a todos los estudiantes de honor de la universidad.
- Para conocer el cereal más popular entre los jóvenes menores de diez años, pararse afuera de un gran supermercado durante tres horas y hablar con cada vigésimo niño menor de diez años que ingresa al supermercado.
- Para encontrar el ingreso promedio anual de todos los adultos en Estados Unidos, muestra congresistas estadounidenses. Crear una muestra de clúster considerando cada estado como un estrato (grupo). Mediante el uso de muestreo aleatorio simple, seleccione estados para formar parte del clúster. Luego encuestar a todos los congresistas estadounidenses en el clúster.
- Para determinar la proporción de personas que toman el transporte público al trabajo, encuestar a 20 personas en la ciudad de Nueva York. Realice la encuesta sentándose en Central Park en un banco y entrevistando a todas las personas que se sientan a su lado.
- Para determinar el costo promedio de una estadía de dos días en un hospital de Massachusetts, realice encuestas a 100 hospitales de todo el estado mediante muestreo aleatorio simple.
Variación en los datos
La variación está presente en cualquier conjunto de datos. Por ejemplo, las latas de bebida de 16 onzas pueden contener más o menos de 16 onzas de líquido. En un estudio, se midieron ocho latas de 16 onzas y produjeron la siguiente cantidad (en onzas) de bebida:
15.8; 16.1; 15.2; 14.8; 15.8; 15.9; 16.0; 15.5
Las mediciones de la cantidad de bebida en una lata de 16 onzas pueden variar porque diferentes personas hacen las medidas o porque la cantidad exacta, 16 onzas de líquido, no se puso en las latas. Los fabricantes realizan pruebas regularmente para determinar si la cantidad de bebida en una lata de 16 onzas cae dentro del rango deseado.
Tenga en cuenta que a medida que toma datos, sus datos pueden variar algo de los datos que otra persona está tomando para el mismo propósito. Esto es completamente natural. Sin embargo, si dos o más de ustedes están tomando los mismos datos y obtienen resultados muy diferentes, es hora de que usted y los demás reevalúen sus métodos de toma de datos y su precisión.
Variación en Muestras
Se mencionó anteriormente que dos o más muestras de una misma población, tomadas al azar, y que tienen cerca de las mismas características de la población probablemente serán diferentes entre sí. Supongamos que Doreen y Jung deciden estudiar la cantidad promedio de tiempo que los estudiantes de su universidad duermen cada noche. Doreen y Jung toman muestras cada una de 500 estudiantes. Doreen utiliza muestreo sistemático y Jung utiliza muestreo por conglomerados. La muestra de Doreen será diferente de la muestra de Jung. Aunque Doreen y Jung usaran el mismo método de muestreo, con toda probabilidad sus muestras serían diferentes. Tampoco estaría equivocado, sin embargo.
Piensa en lo que contribuye a hacer diferentes las muestras de Doreen y Jung.
Si Doreen y Jung tomaron muestras más grandes (es decir, se incrementa el número de valores de datos), los resultados de sus muestras (la cantidad promedio de tiempo que un estudiante duerme) podrían estar más cerca del promedio poblacional real. Pero aún así, sus muestras serían, con toda probabilidad, diferentes entre sí. Esta variabilidad en las muestras no puede ser suficientemente estresada.
Tamaño de una muestra
El tamaño de una muestra (a menudo llamado número de observaciones) es importante. Los ejemplos que has visto en este libro hasta ahora han sido pequeños. Muestras de sólo unos pocos cientos de observaciones, o incluso más pequeñas, son suficientes para muchos propósitos. En sondeo, las muestras que son de 1,200 a 1,500 observaciones se consideran lo suficientemente grandes y lo suficientemente buenas si la encuesta es aleatoria y está bien hecha. Aprenderás por qué cuando estudias intervalos de confianza.
Tenga en cuenta que muchas muestras grandes están sesgadas. Por ejemplo, las encuestas de llamadas son invariablemente sesgadas, porque la gente elige responder o no.
Ejercicio Colaborativo\(\PageIndex{8}\)
Dividir en grupos de dos, tres o cuatro. Su instructor le dará a cada grupo un dado de seis lados. Prueba este experimento dos veces. Enrolle un dado justo (seis lados) 20 veces. Registre el número de unos, dos, tres, cuatro, cinco y seis que obtenga en la siguiente tabla (“frecuencia” es el número de veces que ocurre una cara particular del dado):
| Primer experimento (20 rollos) | Segundo Experimento (20 rollos) | |||
|---|---|---|---|---|
| Cara en la matriz | Frecuencia | Cara en la matriz | Frecuencia | |
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 | ||||
| 6 | ||||
¿Los dos experimentos tuvieron los mismos resultados? Probablemente no. Si hiciste el experimento por tercera vez, ¿esperas que los resultados sean idénticos al primer o segundo experimento? ¿Por qué o por qué no?
¿Qué experimento tuvo los resultados correctos? Ambos lo hicieron. El trabajo del estadístico es ver a través de la variabilidad y sacar conclusiones adecuadas.
Evaluación Crítica
Necesitamos evaluar críticamente los estudios estadísticos sobre los que leemos y analizarlos antes de aceptar los resultados de los estudios. Los problemas comunes a tener en cuenta incluyen
- Problemas con las muestras: Una muestra debe ser representativa de la población. Una muestra que no es representativa de la población está sesgada. Las muestras sesgadas que no son representativas de la población dan resultados inexactos y no válidos.
- Muestras autoseleccionadas: Las respuestas solo de las personas que eligen responder, como las encuestas de llamadas, a menudo no son confiables.
- Problemas con el tamaño de la muestra: Las muestras que son demasiado pequeñas pueden no ser confiables. Las muestras más grandes son mejores, si es posible. En algunas situaciones, tener muestras pequeñas es inevitable y todavía se puede utilizar para sacar conclusiones. Ejemplos: pruebas de choque de autos o pruebas médicas para afecciones raras
- Influencia indebida: recopilar datos o hacer preguntas de una manera que influya en la respuesta
- Inrespuesta o negativa de sujeto a participar: Las respuestas recopiladas pueden dejar de ser representativas de la población. A menudo, las personas con opiniones positivas o negativas fuertes pueden responder encuestas, lo que puede afectar los resultados.
- Causalidad: Una relación entre dos variables no significa que una cause que ocurra la otra. Pueden estar relacionados (correlacionados) por su relación a través de una variable diferente.
- Estudios autofinanciados o de interés propio: Un estudio realizado por una persona u organización con el fin de sustentar su reclamo. ¿El estudio es imparcial? Lea el estudio detenidamente para evaluar el trabajo. No asuma automáticamente que el estudio es bueno, pero tampoco asuma automáticamente que el estudio es malo. Evaluarlo sobre sus méritos y el trabajo realizado.
- Uso engañoso de datos: gráficos mostrados incorrectamente, datos incompletos o falta de contexto
- Confundir: Cuando no se pueden separar los efectos de múltiples factores sobre una respuesta. La confusión hace difícil o imposible sacar conclusiones válidas sobre el efecto de cada factor.
Referencias
- Índice de Bienestar Gallup-Healthways. http://www.well-beingindex.com/default.asp (consultado el 1 de mayo de 2013).
- Índice de Bienestar Gallup-Healthways. http://www.well-beingindex.com/methodology.asp (consultado el 1 de mayo de 2013).
- Índice de Bienestar Gallup-Healthways. http://www.gallup.com/poll/146822/ga...questions.aspx (consultado el 1 de mayo de 2013).
- Datos de www.Bookofodds.com/Relacionsh... -El Presidente
- Dominic Lusinchi, “'Presidente' Landon y la Encuesta Literaria de 1936: ¿Fueron los propietarios de automóviles y teléfonos los culpables?” Historia de las Ciencias Sociales 36, núm. 1:23-54 (2012), ssh.dukejournals.org/content/36/1/23.abstract (consultado el 1 de mayo de 2013).
- “The Literary Digest Poll”, Laboratorios Virtuales en Probabilidad y Estadística http://www.math.uah.edu/stat/data/LiteraryDigest.html (consultado el 1 de mayo de 2013).
- “Prueba de elecciones presidenciales de Gallup: tendencias de calor, 1936—2008”, Gallup Politics http://www.gallup.com/poll/110548/ga...9362004.aspx#4 (consultado el 1 de mayo de 2013).
- The Data and Story Library, lib.stat.cmu.edu/dasl/datafiles/uscrime.html (consultado el 1 de mayo de 2013).
- Datos del programa de Aprendizaje a Distancia (DL) LBCC en 2010-2011, http://de.lbcc.edu/reports/2010-11/f...hts.html#focus (consultado el 1 de mayo de 2013).
- Datos de San Jose Mercury News
Revisar
Los datos son elementos individuales de información que provienen de una población o muestra. Los datos pueden clasificarse como cualitativos, cuantitativos continuos o cuantitativos discretos.
Debido a que no es práctico medir toda la población en un estudio, los investigadores utilizan muestras para representar a la población. Una muestra aleatoria es un grupo representativo de la población elegida mediante un método que da a cada individuo de la población las mismas posibilidades de ser incluido en la muestra. Los métodos de muestreo aleatorio incluyen muestreo aleatorio simple, muestreo estratificado, muestreo por conglomerados y muestreo sistemático. El muestreo de conveniencia es un método no aleatorio para elegir una muestra que a menudo produce datos sesgados.
Las muestras que contienen diferentes individuos dan como resultado diferentes datos. Esto es cierto incluso cuando las muestras son bien elegidas y representativas de la población. Cuando se seleccionan adecuadamente, las muestras más grandes modelan la población más estrechamente que las muestras más pequeñas. Hay muchos problemas potenciales diferentes que pueden afectar la confiabilidad de una muestra. Los datos estadísticos necesitan ser analizados críticamente, no simplemente aceptados.
Notas al pie
- lastbaldeagle. 2013. El Día de Impuestos, Casa llamará a despedir a trabajadores federales que adeudan impuestos atrasados. Encuesta de opinión publicada en línea en: www.youpolls.com/details. aspx`id=12328 (consultado el 1 de mayo de 2013).
- Scott Keeter et al., “Gauging the Impact of Growing Nonresponse on Estimated from a National RDD Telephone Survey”, Public Opinion Quarterly 70 núm. 5 (2006), http://poq.oxfordjournals.org/content/70/5/759.full (consultado el 1 de mayo de 2013).
- Preguntas frecuentes, Pew Research Center for the People & the Press, www.people-press.org/methodol... wer-your-polls (consultado el 1 de mayo de 2013).
Glosario
- Muestreo en raci
- un método para seleccionar una muestra aleatoria y dividir la población en grupos (clusters); utilizar muestreo aleatorio simple para seleccionar un conjunto de clusters. En la muestra se incluye a cada individuo de los conglomerados elegidos.
- Variable aleatoria continua
- una variable aleatoria (RV) cuyos resultados se miden; la altura de los árboles en el bosque es un RV continuo.
- Muestreo Conveniente
- un método no aleatorio para seleccionar una muestra; este método selecciona individuos que son fácilmente accesibles y pueden resultar en datos sesgados.
- Variable aleatoria discreta
- una variable aleatoria (RV) cuyos resultados se cuentan
- Error de no muestreo
- un problema que afecta la confiabilidad de los datos de muestreo distintos de la variación natural; incluye una variedad de errores humanos, incluyendo un diseño deficiente del estudio, métodos de muestreo sesgados, información inexacta proporcionada por los participantes del estudio, errores de entrada de datos y análisis deficientes.
- Datos Cualitativos
- Ver Datos.
- Datos Cuantitativos
- Ver Datos.
- Muestreo Aleatorio
- un método de selección de una muestra que da a cada miembro de la población la misma oportunidad de ser seleccionado.
- Sesgo de muestreo
- no todos los miembros de la población tienen la misma probabilidad de ser seleccionados
- Error de Muestreo
- la variación natural que resulta de seleccionar una muestra para representar una población mayor; esta variación disminuye a medida que aumenta el tamaño de la muestra, por lo que seleccionar muestras más grandes reduce el error de muestreo.
- Muestreo con Repuesto
- Una vez seleccionado a un miembro de la población para su inclusión en una muestra, ese miembro es devuelto a la población para la selección del siguiente individuo.
- Muestreo sin Repuesto
- Un miembro de la población podrá ser elegido para su inclusión en una muestra solo una vez. Si se elige, el miembro no es devuelto a la población antes de la siguiente selección.
- Muestreo aleatorio simple
- un método sencillo para seleccionar una muestra aleatoria; dar un número a cada miembro de la población. Utilice un generador de números aleatorios para seleccionar un conjunto de etiquetas. Estas etiquetas seleccionadas al azar identifican a los miembros de su muestra.
- Muestreo estratificado
- un método para seleccionar una muestra aleatoria utilizada para asegurar que los subgrupos de la población estén representados adecuadamente; dividir la población en grupos (estratos). Utilice un muestreo aleatorio simple para identificar un número proporcional de individuos de cada estrato.
- Muestreo sistemático
- un método para seleccionar una muestra aleatoria; enumerar los miembros de la población. Utilice un muestreo aleatorio simple para seleccionar un punto de partida en la población. Dejar k = (número de individuos en la población)/(número de individuos necesarios en la muestra). Elija cada késimo individuo de la lista comenzando por el que se seleccionó aleatoriamente. Si es necesario, regresa al inicio del listado poblacional para completar tu muestra.


