10.4: Comparando dos proporciones de población independientes
- Page ID
- 153303
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Al realizar una prueba de hipótesis que compare dos proporciones poblacionales independientes, deben estar presentes las siguientes características:
- Las dos muestras independientes son simples muestras aleatorias que son independientes.
- El número de éxitos es de al menos cinco, y el número de fracasos es de al menos cinco, para cada una de las muestras.
- La literatura creciente afirma que la población debe tener al menos diez o 20 veces el tamaño de la muestra. Esto evita que cada población sea sobremuestreada y cause resultados incorrectos.
Comparar dos proporciones, como comparar dos medias, es común. Si dos proporciones estimadas son diferentes, puede deberse a una diferencia en las poblaciones o puede deberse a la casualidad. Una prueba de hipótesis puede ayudar a determinar si una diferencia en las proporciones estimadas refleja una diferencia en las proporciones de la población.
La diferencia de dos proporciones sigue una distribución normal aproximada. Generalmente, la hipótesis nula establece que las dos proporciones son las mismas. Es decir,\(H_{0}: p_{A} = p_{B}\). Para realizar la prueba, utilizamos una proporción agrupada,\(p_{c}\).
La proporción agrupada se calcula de la siguiente manera:
\[p_{c} = \dfrac{x_{A} + x_{B}}{n_{A} + n_{B}}\]
La distribución de las diferencias es:
\[P\_{A} - P'_{b} N\left[0, \sqrt{p_{c}(1 - p_{c})\left(\dfrac{1}{n_{A}} + \dfrac{1}{n_{B}}\right)}\right]\]
El estadístico de prueba (z -score) es:
\[z = \dfrac{(p'_{A} - p'_{B}) - (p_{A} - p_{B})}{\sqrt{p_{c}(1 - p_{c})\left(\dfrac{1}{n_{A}} + \dfrac{1}{n_{B}}\right)}}\]
Ejemplo\(\PageIndex{1}\)
Se están probando dos tipos de medicamentos para colmenas para determinar si hay diferencia en las proporciones de reacciones de pacientes adultos. Veinte de una muestra aleatoria de 200 adultos a los que se les administró el medicamento A todavía tenían urticaria 30 minutos después de tomar el medicamento. Doce de otra muestra aleatoria de 200 adultos a los que se administró el medicamento B aún presentaban urticaria 30 minutos después de tomar el medicamento. Prueba a un nivel de significancia del 1%.
Contestar
El problema pide una diferencia de proporciones, convirtiéndola en una prueba de dos proporciones.
Dejar\(A\) y\(B\) ser los subíndices para la medicación A y la medicación B, respectivamente. Entonces\(p_{A}\) y\(p_{B}\) son las proporciones poblacionales deseadas.
Variable aleatoria:\(P′_{A} – P′_{B} =\) diferencia en las proporciones de pacientes adultos que no reaccionaron después de 30 minutos a la medicación A y a la medicación B.
\(H_{0}: p_{A} = p_{B}\)
\(p_{A} - p_{B} = 0\)
\(H_{a}: p_{A} \neq p_{B}\)
\(p_{A} - p_{B} \neq 0\)
Las palabras “es una diferencia” te dicen que la prueba es de dos colas.
Distribución para la prueba: Dado que se trata de una prueba de dos proporciones binomiales de población, la distribución es normal:
\[p_{c} = \dfrac{x_{A} + x_{B}}{n_{A} + n_{B}} = \dfrac{20 + 12}{200 + 200} = 800 1 - p_{c} = 0.92\]
\[P'_{A} - P'_{B} - N\left[0, \sqrt{(0.08)(0.92)\left(\dfrac{1}{200} + \dfrac{1}{200}\right)}\right]\]
\(P'_{A} - P'_{B}\)sigue una distribución normal aproximada.
Calcular el valor p usando la distribución normal:\(p\text{-value} = 0.1404\).
Proporción estimada para el grupo A:\(p'_{A} = \dfrac{x_{A}}{n_{A}} = \dfrac{20}{200} = 0.1\)
Proporción estimada para el grupo B:\(p'_{B} = \dfrac{x_{B}}{n_{B}} = \dfrac{12}{200} = 0.06\)
Gráfica:
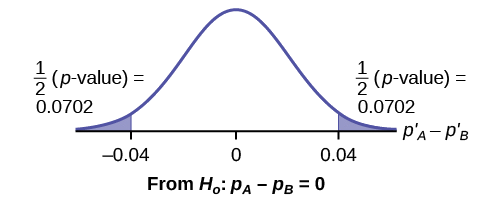
\(P′_{A} - P′_{B} = 0.1 – 0.06 = 0.04\).
La mitad\(p\text{-value}\) está por debajo de -0.04, y la mitad está por encima de 0.04.
Comparar\(\alpha\) y el\(p\text{-value}: \alpha = 0.01\) y el\(p\text{-value} = 0.1404\). \(\alpha < p\text{-value}\).
Tomar una decisión: Ya que\(\alpha < p\text{-value}\), no rechace\(H_{0}\).
Conclusión: A un nivel de significancia de 1%, a partir de los datos de la muestra, no hay evidencia suficiente para concluir que existe una diferencia en las proporciones de pacientes adultos que no reaccionaron después de 30 minutos a la medicación A y la medicación B.
Presione STAT. Flecha sobre PRUEBAS y presiona 6:2 -PROPzTest. Flecha hacia abajo e ingresa 20 para x1, 200 para n1, 12 para x2 y 200 para n2. Flecha abajo a p1: y flecha para no igualar p2. Presione ENTER. Flecha hacia abajo para Calcular y presiona ENTRAR. El valor p es p = 0.1404 y el estadístico de prueba es 1.47. Vuelva a hacer el procedimiento, pero en lugar de Calcular hacer Dibujar.
Ejercicio\(\PageIndex{1}\)
Se están probando dos tipos de válvulas para determinar si hay una diferencia en las tolerancias de presión. Quince de una muestra aleatoria de 100 de Válvula A agrietada bajo 4,500 psi. Seis de una muestra aleatoria de 100 de la Válvula B agrietada bajo 4,500 psi. Prueba a un nivel de significancia del 5%.
Contestar
El\(p\text{-value}\) es 0.0379, por lo que podemos rechazar la hipótesis nula. Al nivel de significancia del 5%, los datos apoyan que existe una diferencia en las tolerancias de presión entre las dos válvulas.
Ejemplo\(\PageIndex{2}\): Sexting
Se realizó un estudio de investigación sobre las diferencias de género en el “sexting”. El investigador consideró que la proporción de niñas involucradas en el “sexting” es menor que la proporción de niños involucrados. Los datos recopilados en la primavera de 2010 entre una muestra aleatoria de estudiantes de secundaria y preparatoria en un distrito escolar grande en el sur de Estados Unidos se resumen en la Tabla. ¿La proporción de niñas que envían sextos es menor que la proporción de chicos “sexting”? Prueba a un nivel de significancia del 1%.
| Machos | Hembras | |
|---|---|---|
| Enviaron “sextos” | 183 | 156 |
| Número total encuestados | 2231 | 2169 |
Contestar
Esta es una prueba de dos proporciones poblacionales. Sea M y F los subíndices para machos y hembras. Entonces\(p_{M}\) y\(p_{F}\) son las proporciones poblacionales deseadas.
Variable aleatoria:\(p'_{F} - p'_{M} =\) diferencia en las proporciones de machos y hembras que enviaron “sextos”.
\(H_{a}: p_{F} = p_{m} H_{0}: p_{F} - p_{M} = 0\)
\(H_{a}: p_{F} < p_{m} H_{a}: p_{F} - p_{M} < 0\)
Las palabras “menos que” te dicen que la prueba es de cola izquierda.
Distribución para la prueba: Dado que se trata de una prueba de dos proporciones poblacionales, la distribución es normal:
\[p_{C} = \dfrac{x_{F} + x_{M}}{n_{F} + n_{M}} = \dfrac{156 + 183}{2169 + 2231} = 0.077\]
\[1 - p_{C} = 0.923\]
Por lo tanto,
\[p'_{F} - p'_{M} \sim N\left(0, \sqrt{(0.077)(0.923)\left(\dfrac{1}{2169} + \dfrac{1}{2231}\right)}\right)\]
\(p′_{F} – p′_{M}\)sigue una distribución normal aproximada.
Calcular el\(p\text{-value}\) usando la distribución normal:
\(p\text{-value} = 0.1045\)
Proporción estimada para mujeres: 0.0719
Proporción estimada para hombres: 0.082
Gráfica:
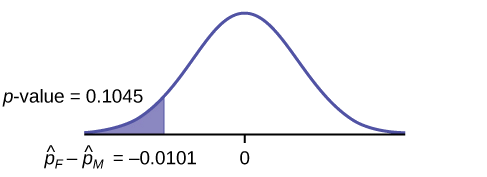
Decisión: Desde\(\alpha < p\text{-value}\), No Rechazar\(H_{0}\)
Conclusión: Al nivel de significancia del 1%, a partir de los datos de la muestra, no hay evidencia suficiente para concluir que la proporción de niñas que envían “sextos” es menor que la proporción de niños que envían “sextos”.
Presione STAT. Flecha sobre PRUEBAS y presiona 6:2 -PROPzTest. Flecha hacia abajo e ingresa 156 para x1, 2169 para n1, 183 para x2 y 2231 para n2. Flecha hacia abajo a p1: y flecha a menos de p2. Presione ENTER. Flecha hacia abajo para Calcular y presiona ENTRAR. El\(p\text{-value}\) es\(P = 0.1045\) y el estadístico de prueba es\(z = -1.256\).
Ejemplo\(\PageIndex{3}\)
Los investigadores realizaron un estudio sobre el uso de teléfonos inteligentes entre adultos. Una compañía de telefonía celular afirmó que los teléfonos inteligentes iPhone son más populares entre los blancos (no hispanos) que entre los afroamericanos. Los resultados de la encuesta indican que de los 232 propietarios de celulares afroamericanos muestreados aleatoriamente, 5% tienen un iPhone. De los 1,343 propietarios de celulares blancos muestreados aleatoriamente, el 10% posee un iPhone. Prueba al nivel de significancia del 5%. ¿La proporción de propietarios de iPhone blancos es mayor que la proporción de propietarios de iPhone afroamericanos?
Contestar
Esta es una prueba de dos proporciones poblacionales. Que W y A sean los subíndices para los blancos y afroamericanos. Entonces p W y p A son las proporciones poblacionales deseadas.
Variable aleatoria:\(p′_{W} – p′_{A} =\) diferencia en las proporciones de usuarios de Android y iPhone.
\(H_{0}: p_{W} = p_{A} H_{0}: p_{W} – p_{A} = 0\)
\(H_{a}: p_{W} > p_{A} H_{a}: p_{W} – p_{A} < 0\)
Las palabras “más populares” indican que la prueba es de cola derecha.
Distribución para la prueba: La distribución es aproximadamente normal:
\[p_{C} = \dfrac{x_{W} + x_{A}}{n_{W} + n_{A}} = \dfrac{134 + 12}{1343 + 232} = 0.0927\]
\[1 - p_{C} = 0.9073\]
Por lo tanto,
\[p'_{W} - p'_{A} \sim N\left(0, \sqrt{(0.0927)(0.9073)\left(\dfrac{1}{1343} + \dfrac{1}{232}\right)}\right)\]
\(p'_{W} - p'_{A}\)sigue una distribución normal aproximada.
Calcular el\(p\text{-value}\) usando la distribución normal:
\(p\text{-value} = 0.0077\)
Proporción estimada para el grupo A: 0.10
Proporción estimada para el grupo B: 0.05
Gráfica:
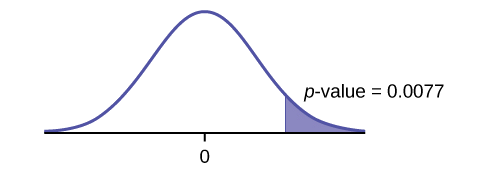
Decisión: Ya que\(\alpha > p\text{-value}\), rechazar el\(H_{0}\).
Conclusión: En el nivel de significancia del 5%, a partir de los datos de la muestra, hay evidencia suficiente para concluir que una mayor proporción de propietarios de teléfonos celulares blancos usan iPhones que los afroamericanos.
TI-83+ y TI-84: Presione STAT. Flecha sobre PRUEBAS y presiona 6:2 -PROPzTest. Flecha hacia abajo e ingresa 135 para x1, 1343 para n1, 12 para x2 y 232 para n2. Flecha hacia abajo a p1: y flecha a mayor que p2. Presione ENTER. Flecha hacia abajo para Calcular y presiona ENTRAR. El valor P es P = 0.0092 y el estadístico de prueba es Z = 2.33.
Ejemplo\(\PageIndex{3}\)
Un grupo preocupado de ciudadanos quería saber si la proporción de violaciones forzadas en Texas era diferente en 2011 que en 2010. Su investigación mostró que de los 113 mil 231 delitos violentos ocurridos en Texas en 2010, 7 mil 622 de ellos fueron violaciones forzadas. En 2011, 7 mil 439 de los 104 mil 873 delitos violentos se encontraban en la categoría de violación forzosa. Prueba a un nivel de significancia del 5%. Responde las siguientes preguntas:
- ¿Es esto una prueba de dos medias o dos proporciones?
- ¿Qué distribución utilizas para realizar la prueba?
- ¿Cuál es la variable aleatoria?
- ¿Cuáles son las hipótesis nula y alternativa? Escribir la hipótesis nula y alternativa en símbolos.
- ¿Esta prueba es derecha, izquierda o de dos colas?
- ¿Cuál es el\(p\text{-value}\)?
- ¿Rechazas o no rechazas la hipótesis nula?
- En el nivel ___ de significancia, a partir de los datos de la muestra, hay ______ (es/no es) evidencia suficiente para concluir que ____________.
Soluciones
a. dos proporciones
b. normal para dos proporciones
c. Subíndices: 1 = 2010, 2 = 2011\(P′_{1} - P′_{2}\)
d. Subíndices: 1 = 2010, 2 = 2011\(H_{0}: p_{1} = p_{2} H_{0}: p_{1} − p_{2} = 0\)\(H_{0}: p_{1} \neq p_{2} H_{0}: p_{1} − p_{2} \neq 0\)
e. De dos colas
f.\(p\text{-value} = 0.00086\)
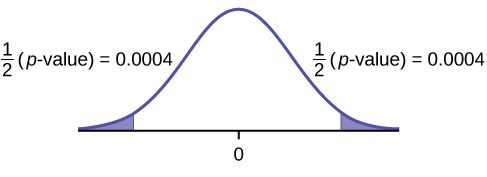
g. Rechazar el\(H_{0}\).
h. Al nivel de significancia del 5%, a partir de los datos de la muestra, hay evidencia suficiente para concluir que existe una diferencia entre la proporción de violaciones forzadas en 2011 y 2010.
Referencias
- Datos de Recursos Educativos, catálogo de diciembre.
- Datos de Hilton Hotels. Disponible en línea en http://www.hilton.com (consultado el 17 de junio de 2013).
- Datos de Hyatt Hotels. Disponible en línea en hyatt.com (consultado el 17 de junio de 2013).
- Datos de Estadísticas, Departamento de Salud y Servicios Humanos de Estados Unidos.
- Datos de Whitney Exhibit en préstamo al Museo de Arte de San José.
- Datos de la Sociedad Americana contra el Cáncer. Disponible en línea en http://www.cancer.org/index (consultado el 17 de junio de 2013).
- Datos de la Oficina del Canciller, Colegios Comunitarios de California, noviembre de 1994.
- “Estado de los Estados”. Gallup, 2013. Disponible en línea en www.Gallup.com/poll/125066/st... ef=interactive (consultado el 17 de junio de 2013).
- “Virus del Nilo Occidental”. Centros para el Control y Prevención de Enfermedades. Disponible en línea en http://www.cdc.gov/ncidod/dvbid/westnile/index.htm (consultado el 17 de junio de 2013).
Revisar
- Prueba de dos proporciones poblacionales a partir de muestras independientes.
- Variable aleatoria:\(\hat{p}_{A} - \hat{p}_{B} =\) diferencia entre las dos proporciones estimadas
- Distribución: distribución normal
Revisión de Fórmula
Proporción agrupada:
\[p_{c} = \dfrac{x_{F} + x_{M}}{n_{F} + n_{M}}\]
Distribución para las diferencias:
\[p'_{A} - p'_{B} \sim N\left[0, \sqrt{p_{c}(1-p_{c})\left(\dfrac{1}{n_{A}} + \dfrac{1}{n_{B}}\right)}\right]\]
donde la hipótesis nula es\(H_{0}: p_{A} = p_{B}\) o\(H_{0}: p_{A} - p_{B} = 0\).
Estadística de prueba (z -score):
\[z = \dfrac{(p'_{A} - p'_{B})}{\sqrt{p_{c}(1-p_{c})\left(\dfrac{1}{n_{A}} + \dfrac{1}{n_{B}}\right)}}\]
donde la hipótesis nula es\(H_{0}: p_{A} = p_{B}\) o\(H_{0}: p_{A} - p_{B} = 0\).
y
- \(p'_{A}\)y\(p'_{B}\) son las proporciones muestrales,\(p_{A}\) y\(p_{B}\) son las proporciones poblacionales,
- \(P_{c}\)es la proporción agrupada y\(n_{A}\) y\(n_{B}\) son los tamaños de muestra.
Glosario
- Proporción agrupada
- estimación del valor común de\(p_{1}\) y\(p_{2}\).


