12.3: Gráficas de dispersión
- Page ID
- 153226
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Antes de retomar la discusión de regresión lineal y correlación, necesitamos examinar una manera de mostrar la relación entre dos variables x e y. La forma más común y fácil es un diagrama de dispersión. El siguiente ejemplo ilustra un diagrama de dispersión.
Ejemplo\(\PageIndex{1}\)
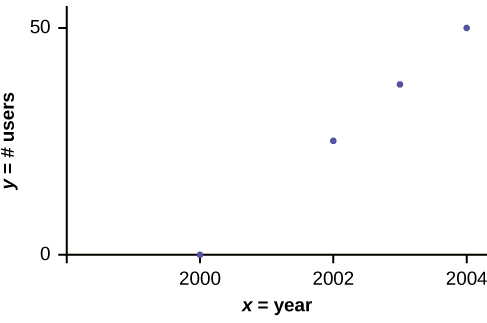
En Europa y Asia, el m-commerce es popular. Los usuarios de M-commerce tienen teléfonos móviles especiales que funcionan como billeteras electrónicas, además de brindar servicios telefónicos e Internet. Los usuarios pueden hacer de todo, desde pagar el estacionamiento hasta comprar un televisor o refresco de una máquina hasta realizar operaciones bancarias hasta verificar resultados deportivos en Internet. Para los años 2000 a 2004, ¿hubo relación entre el año y el número de usuarios de m-commerce? Construir un diagrama de dispersión. Que\(x =\) el año y deje que\(y =\) el número de usuarios de m-commerce, en millones.
| \(x\)(año) | \(y\)(# de usuarios) |
|---|---|
| \ (x\) (año) ">2000 | \ (y\) (# de usuarios) ">0.5 |
| \ (x\) (año) ">2002 | \ (y\) (# de usuarios) ">20.0 |
| \ (x\) (año) ">2003 | \ (y\) (# de usuarios) ">33.0 |
| \ (x\) (año) ">2004 | \ (y\) (# de usuarios) ">47.0 |
Para crear un gráfico de dispersión
- Ingresa tus\(X\) datos en la lista L1 y tus\(Y\) datos en la lista L2.
- Presione 2do STATPLOT ENTRAR para usar la Parcela 1. En la pantalla de entrada para PARCELA 1, resalte Encendido y presione ENTRAR. (Asegúrese de que las otras parcelas estén DESCONECTADAS.)
- Para TYPE: resalta el primer icono, que es el diagrama de dispersión, y presiona ENTRAR.
- Para Xlist:, ingrese L1 ENTER y para Ylist: L2 ENTER.
- Para Mark: no importa qué símbolo resaltes, pero el cuadrado es el más fácil de ver. Presione ENTER.
- Asegúrese de que no haya otras ecuaciones que puedan ser trazadas. Presiona Y = y borra cualquier ecuación.
- Presione la tecla ZOOM y luego el número 9 (para el elemento del menú “ZoomStat”); la calculadora ajustará la ventana a los datos. Puede presionar VENTANA para ver el escalado de los ejes.
Ejercicio\(\PageIndex{1}\)
Amelia juega básquetbol para su preparatoria. Ella quiere mejorar para jugar a nivel universitario. Ella nota que el número de puntos que anota en un juego sube en respuesta a la cantidad de horas que practica su tiro de salto cada semana. Registra los siguientes datos:
| \(X\)(horas practicando tiro en salto) | \(Y\)(puntos anotados en un juego) |
|---|---|
| \ (X\) (horas practicando tiro de salto) ">5 | \ (Y\) (puntos anotados en un juego) ">15 |
| \ (X\) (horas practicando tiro en salto) ">7 | \ (Y\) (puntos anotados en un juego) ">22 |
| \ (X\) (horas practicando tiro en salto) ">9 | \ (Y\) (puntos anotados en un juego) ">28 |
| \ (X\) (horas practicando tiro en salto) ">10 | \ (Y\) (puntos anotados en un juego) ">31 |
| \ (X\) (horas practicando tiro de salto) ">11 | \ (Y\) (puntos anotados en un juego) ">33 |
| \ (X\) (horas practicando tiro de salto) ">12 | \ (Y\) (puntos anotados en un juego) ">36 |
Construye un diagrama de dispersión y establece si lo que Amelia piensa parece ser cierto.
- Contestar
-
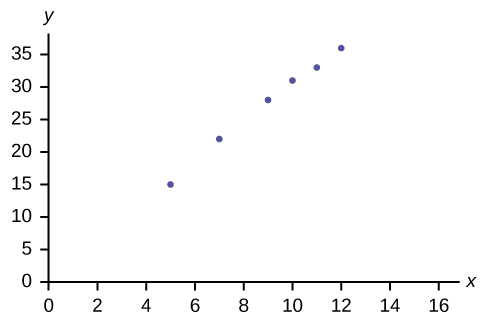
Figura \(\PageIndex{2}\)
Sí, la suposición de Amelia parece ser correcta. El número de puntos que anota Amelia por partido sube cuando practica más su tiro al salto.
Un diagrama de dispersión muestra la dirección de una relación entre las variables. Una dirección clara ocurre cuando hay:
- Valores altos de una variable ocurriendo con valores altos de la otra variable o valores bajos de una variable ocurriendo con valores bajos de la otra variable.
- Los valores altos de una variable ocurren con valores bajos de la otra variable.
Se puede determinar la fuerza de la relación mirando el diagrama de dispersión y viendo qué tan cerca están los puntos de una línea, una función de potencia, una función exponencial, o de algún otro tipo de función. Para una relación lineal hay una excepción. Considera un diagrama de dispersión donde todos los puntos caen sobre una línea horizontal proporcionando un “ajuste perfecto”. De hecho, la línea horizontal no mostraría relación alguna.
Cuando miras un gráfico de dispersión, quieres notar el patrón general y cualquier desviación del patrón. Los siguientes ejemplos de diagramas de dispersión ilustran estos conceptos.
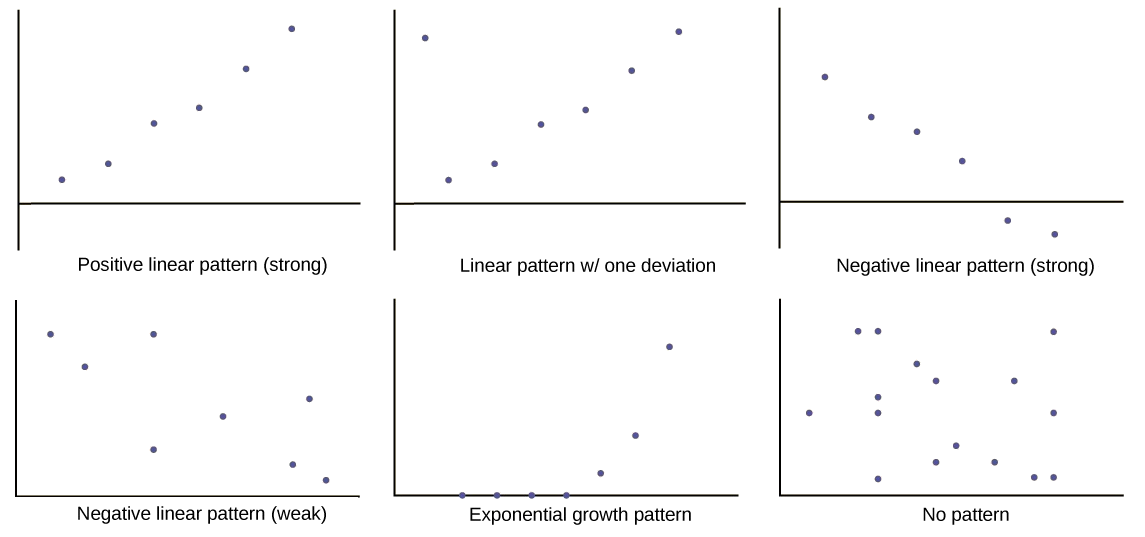
En este capítulo, nos interesan las gráficas de dispersión que muestran un patrón lineal. Los patrones lineales son bastante comunes. La relación lineal es fuerte si los puntos están cerca de una línea recta, excepto en el caso de una línea horizontal donde no hay relación. Si pensamos que los puntos muestran una relación lineal, nos gustaría trazar una línea en el diagrama de dispersión. Esta línea se puede calcular a través de un proceso llamado regresión lineal. Sin embargo, solo calculamos una línea de regresión si una de las variables ayuda a explicar o predecir la otra variable. Si\(x\) es la variable independiente y\(y\) la variable dependiente, entonces podemos usar una línea de regresión para predecir\(y\) para un valor dado de\(x\)
Resumen
Los gráficos de dispersión son particularmente útiles cuando queremos ver si existe una relación lineal entre los puntos de datos. Indican tanto la dirección de la relación entre las\(x\) variables y las\(y\) variables, como la fuerza de la relación. Se calcula la fuerza de la relación entre una variable independiente y una variable dependiente mediante regresión lineal.