2.1: Tres pantallas de datos populares
- Page ID
- 151107
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objetivos de aprendizaje
- Aprender a interpretar el significado de tres representaciones gráficas de conjuntos de datos: diagramas de tallo y hoja, histogramas de frecuencia e histogramas de frecuencia relativa.
Un adagio bien conocido es que “una imagen vale más que mil palabras”. Este dicho resulta cierto a la hora de presentar información estadística en un conjunto de datos. Hay muchas formas efectivas de presentar los datos gráficamente. Las tres herramientas gráficas que se introducen en esta sección se encuentran entre las más utilizadas y son relevantes para la posterior presentación del material en este libro.
Diagramas de tallo y hoja
Supongamos que\(30\) los alumnos de una clase de estadística tomaron una prueba y obtuvieron los siguientes puntajes:
\[\begin{array}{r}86 & 80 & 25 & 77 & 73 & 76 & 100 & 90 & 69 & 93 \\ 90 & 83 & 70 & 73 & 73 & 70 & 90 & 83 & 71 & 95 \\ 40 & 58 & 68 & 69 & 100 & 78 & 87 & 97 & 92 & 74\end{array}\]
¿Cómo le fue a la clase en la prueba? Un rápido vistazo al conjunto de\(30\) números no da una respuesta clara de inmediato. Sin embargo, el conjunto de datos puede ser reorganizado y reescrito para hacer más visible la información relevante. Una forma de hacerlo es construir un diagrama de tallo y hoja como se muestra en\(\PageIndex{1}\) la Figura Los números en el lugar de las decenas, de\(2\) a través\(9\), y adicionalmente el número\(10\), son los “tallos”, y están dispuestos en orden numérico de arriba a abajo a la izquierda de una línea vertical. El número en el lugar de unidades en cada medida es una “hoja”, y se coloca en una fila a la derecha del tallo correspondiente, el número en el lugar de las decenas de esa medida. Así, las tres hojas\(9, 8, \text{and} \; 9\) en la fila encabezada con el tallo\(6\) corresponden a las tres puntuaciones de examen en la\(60s, 69\) (en la primera fila de datos),\(68\) (en la tercera fila), y\(69\) (también en la tercera fila).

La exhibición se hace aún más útil para algunos propósitos reordenando las hojas en orden numérico, como se muestra en la Figura\(\PageIndex{2}\). De cualquier manera, con los datos reorganizados cierta información de interés se hace evidente de inmediato. Hay dos puntajes perfectos; tres estudiantes obtuvieron puntajes por debajo\(60\); la mayoría de los estudiantes obtuvieron puntajes en el\(70s, 80s\; \text{and} \; 90s\); y el promedio general probablemente esté en el alto\(70s\; \text{or low}\; 80s\).

En este ejemplo las puntuaciones tienen un tallo natural (el lugar de las decenas) y una hoja (el lugar de unos). Uno podría extender el diagrama dividiendo cada número de lugar de decenas en categorías inferior y superior. Por ejemplo, todas las puntuaciones en el\(80s\) pueden representarse en dos tallos separados, inferior\(80s\) y superior\(80s\):
\[\begin{array}{r|lcc}8 & 0 & 3 & 3 \\ 8 & 6 & 7 &\end{array}\]
Las definiciones de tallos y hojas son flexibles en la práctica. El propósito general de un diagrama de tallo y hoja es proporcionar una visualización rápida de cómo se distribuyen los datos en el rango de sus valores; podría ser necesaria cierta improvisación para obtener un diagrama que mejor cumpla con ese objetivo.
Tenga en cuenta que todos los datos originales se pueden recuperar del diagrama de tallo y hoja. Esto no será cierto en los siguientes dos tipos de pantallas gráficas.
Histogramas de frecuencia
El diagrama de tallo y hoja no es práctico para grandes conjuntos de datos, por lo que necesitamos una forma diferente, puramente gráfica para representar los datos. Un histograma de frecuencia es un dispositivo de este tipo. Lo ilustraremos usando el mismo conjunto de datos de la subsección anterior. Para las\(30\) puntuaciones del examen, es natural agrupar las puntuaciones en la escala estándar de diez puntos, y contar el número de puntajes en cada grupo. Así hay dos\(100s\), siete puntajes en el\(90s\), seis en el\(80s\), y así sucesivamente. Luego construimos el diagrama que se muestra en la Figura\(\PageIndex{3}\) dibujando para cada grupo, o clase, una barra vertical cuya longitud es el número de observaciones en ese grupo. En nuestro ejemplo, la barra etiquetada\(100\) es de\(2\) unidades de largo, la barra etiquetada\(90\) es de\(7\) unidades de largo, y así sucesivamente. Si bien se pierden los valores de los datos individuales, conocemos el número en cada clase. Este número se llama la frecuencia de la clase, de ahí el nombre histograma de frecuencia.
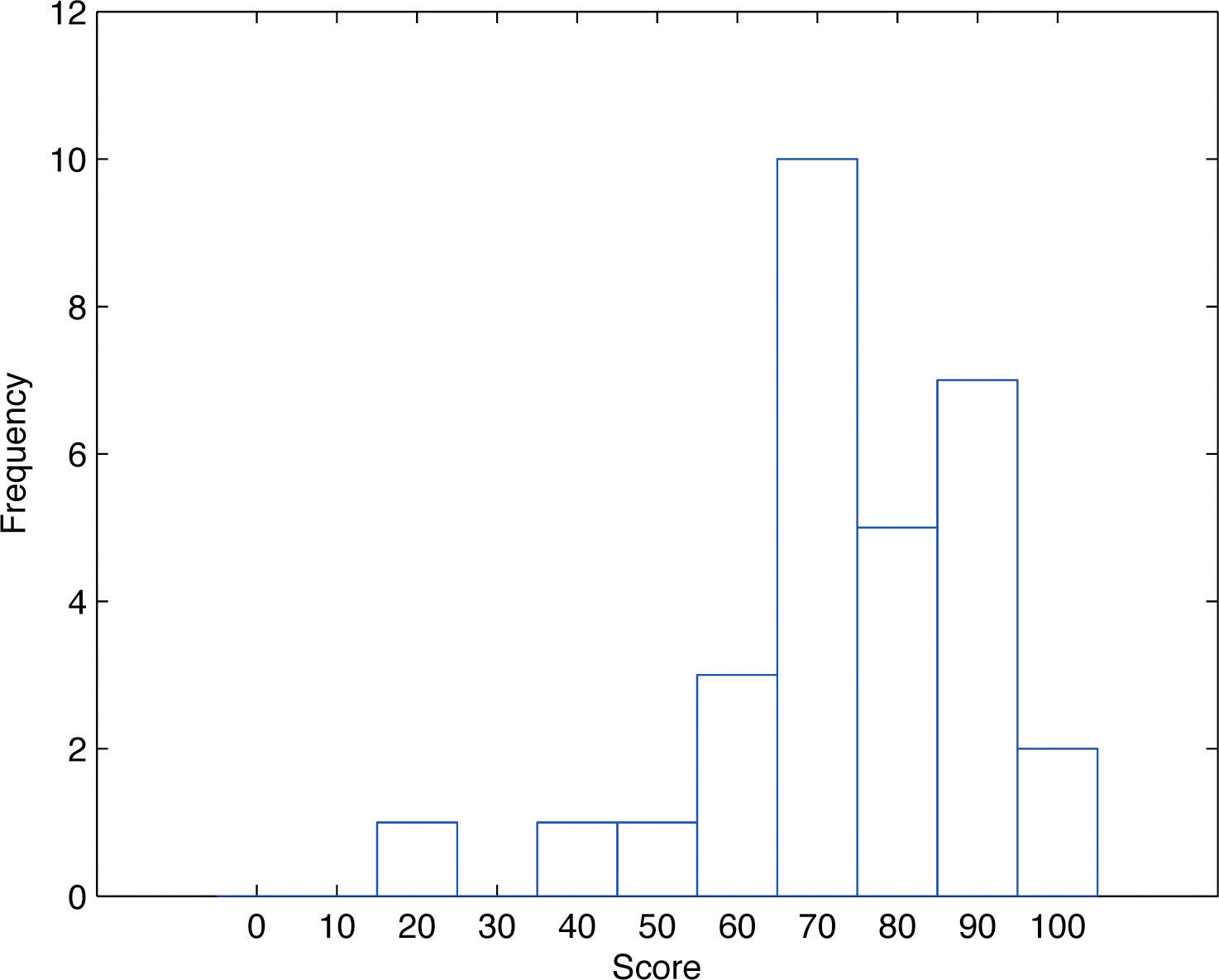
El mismo procedimiento se puede aplicar a cualquier colección de datos numéricos. Las observaciones se agrupan en varias clases y se anota la frecuencia (el número de observaciones) de cada clase. Estas clases se organizan e indican en orden en el eje horizontal (denominado eje x), y para cada grupo se dibuja una barra vertical, cuya longitud es el número de observaciones en ese grupo. La visualización resultante es un histograma de frecuencia para los datos. La similitud en Figura\(\PageIndex{1}\) y Figura\(\PageIndex{3}\) es evidente, particularmente si imagina girar el diagrama de tallo y hoja de lado girándolo un cuarto de vuelta en sentido antihorario.
Definición
En general, la definición de las clases en el histograma de frecuencia es flexible. El propósito general de un histograma de frecuencia es muy similar al de un diagrama de tallo y hoja, para proporcionar una visualización gráfica que dé una sensación de distribución de datos a través del rango de valores que aparecen.
No discutiremos el proceso de construcción de un histograma a partir de datos ya que en la práctica real se realiza automáticamente con software estadístico o incluso calculadoras portátiles.
Histogramas de frecuencia relativa
En nuestro ejemplo de las puntuaciones de los exámenes en una clase de estadística, cinco alumnos anotaron en el\(80s\). El número\(5\) es la frecuencia del grupo etiquetado como “\(80s\).” Ya que hay\(30\) alumnos en toda la clase de estadística, la proporción que puntuaron en la\(80s\) es\(5/30\). El número\(5/30\), que también podría expresarse como\(0.1 \bar{6} \approx . 1667\), o como\(16.67\% \), es la frecuencia relativa del grupo etiquetado como “”\(80s\). Cada grupo (el\(70s\), el\(80s\), y así sucesivamente) tiene una frecuencia relativa. Así podemos construir un diagrama dibujando para cada grupo, o clase, una barra vertical cuya longitud es la frecuencia relativa de ese grupo. Por ejemplo, la barra para el\(80s\) tendrá\(5/30\) unidad de longitud, no\(5\) unidades. El diagrama es un histograma de frecuencia relativa para los datos, y se muestra en la Figura\(\PageIndex{4}\). Es exactamente lo mismo que el histograma de frecuencia excepto que el eje vertical en el histograma de frecuencia relativa no es frecuencia sino frecuencia relativa.
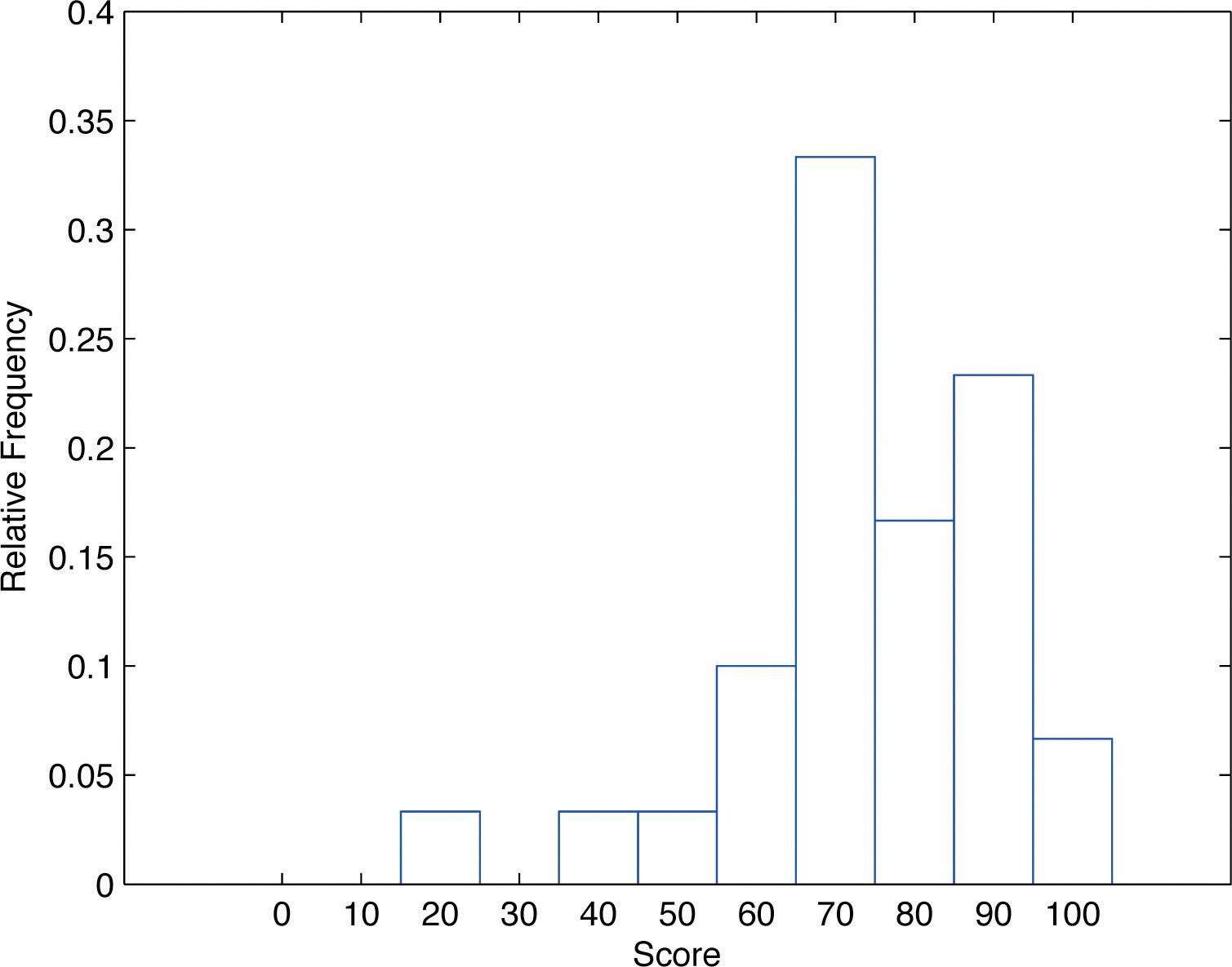
El mismo procedimiento se puede aplicar a cualquier colección de datos numéricos. Se seleccionan clases, se anota la frecuencia relativa de cada clase, las clases se organizan e indican en orden en el eje horizontal, y para cada clase se dibuja una barra vertical, cuya longitud es la frecuencia relativa de la clase. La visualización resultante es un histograma de frecuencia relativa para los datos. Un punto clave es que ahora si cada barra vertical tiene\(1\) unidad de ancho, entonces el área total de todas las barras es\(1\) o\(100\% \).
Si bien los histogramas en Figura\(\PageIndex{3}\) y Figura\(\PageIndex{4}\) tienen la misma apariencia, el histograma de frecuencia relativa es más importante para nosotros, y serán histogramas de frecuencia relativa los que se utilizarán repetidamente para representar datos en este texto. Para ver por qué esto es así, reflexiona sobre qué es lo que realmente estás viendo en los diagramas que te comunican de manera rápida y efectiva información sobre los datos. Son los tamaños relativos de las barras. La barra etiquetada como “\(70s\)” en cualquiera\(1/3\) de las figuras ocupa el área total de todas las barras, y aunque quizá no pensemos en esto conscientemente, percibimos la proporción\(1/3\) en las cifras, lo que indica que un tercio de las calificaciones estaban en el\(70s\). El histograma de frecuencia relativa es importante porque el etiquetado en el eje vertical refleja lo que es importante visualmente: los tamaños relativos de las barras.
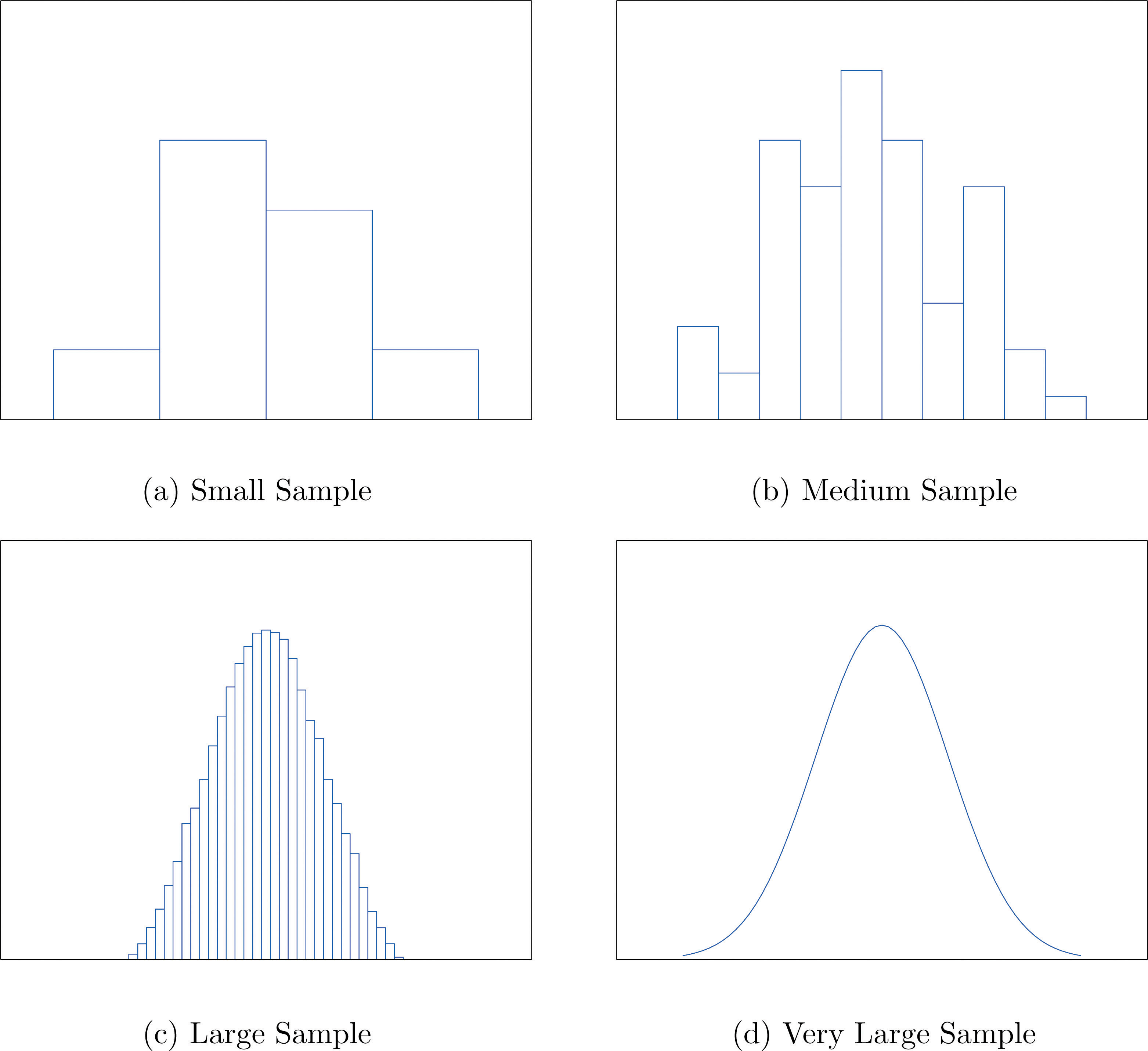
Cuando el tamaño n de una muestra es pequeño, solo se pueden usar unas pocas clases para construir un histograma de frecuencia relativa. Tal histograma podría parecerse al del panel (a) de la Figura\(\PageIndex{5}\). Si\(n\) se incrementara el tamaño de la muestra, entonces se podrían utilizar más clases en la construcción de un histograma de frecuencia relativa y las barras verticales del histograma resultante serían más finas, como se indica en el panel (b) de la Figura\(\PageIndex{5}\). Para una muestra muy grande el histograma de frecuencia relativa se vería muy fino, como el de (c) de la Figura\(\PageIndex{5}\). Si el tamaño de la muestra aumentara indefinidamente entonces el histograma de frecuencia relativa correspondiente sería tan fino que se vería como una curva suave, como la del panel (d) de la Figura\(\PageIndex{5}\).
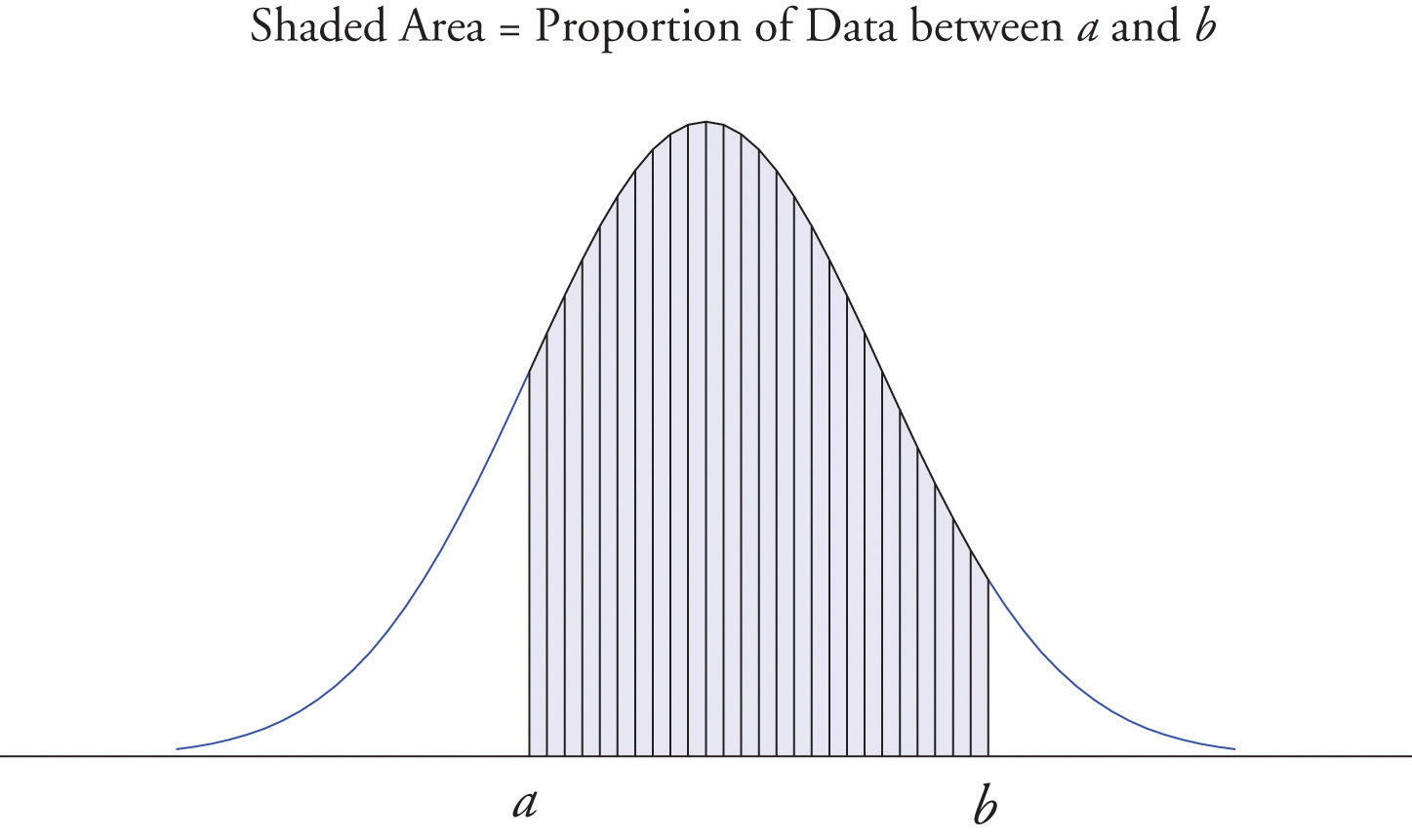
Es común en las estadísticas representar una población o un conjunto de datos muy grande mediante una curva suave. Es bueno tener en cuenta que tal curva es en realidad solo un histograma de frecuencia relativa muy fino en el que han desaparecido las barras verticales sumamente estrechas. Debido a que el área de cada barra vertical de este tipo es la proporción de los datos que se encuentra en el intervalo de números sobre el que se encuentra esa barra, esto significa que para dos números cualesquiera\(a\) y\(b\), la proporción de los datos que se encuentra entre los dos números\(a\) y\(b\) es el área debajo del curva que está por encima del intervalo (\(a,b\)) en el eje horizontal. Esta es la zona que se muestra en la Figura\(\PageIndex{6}\). En particular el área total bajo la curva es\(1\), o\(100\% \).
Llave para llevar
- Las representaciones gráficas de grandes conjuntos de datos proporcionan una visión general rápida de la naturaleza de los datos.
- Una población o un conjunto de datos muy grande pueden estar representados por una curva suave. Esta curva es un histograma de frecuencia relativa muy fino en el que se han omitido las barras verticales sumamente estrechas.
- Cuando se utiliza una curva derivada de un histograma de frecuencia relativa para describir un conjunto de datos, la proporción de datos con valores entre dos números\(a\) y\(b\) es el área bajo la curva entre\(a\) y\(b\), como se ilustra en la Figura\(\PageIndex{6}\).

