7.2: Estimación de muestra pequeña de una media poblacional
- Page ID
- 151200
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objetivos de aprendizaje
- Familiarizarse con la\(t\) distribución de Student.
- Comprender cómo aplicar fórmulas adicionales para un intervalo de confianza para una media poblacional.
Las fórmulas de intervalo de confianza en la sección anterior se basan en el Teorema de Límite Central, la afirmación de que para muestras grandes normalmente\(\overline{X}\) se distribuye con media\(\mu\) y desviación estándar\(\sigma /\sqrt{n}\). Cuando\(\mu\) se estima la media poblacional con una muestra pequeña (\(n<30\)), no se aplica el Teorema del Límite Central. Para proceder asumimos que la población numérica de la que se toma la muestra tiene una distribución normal para empezar. Si se cumple esta condición, entonces cuando\(\sigma\) se conoce la desviación estándar de la población, la fórmula antigua aún se\(\bar{x}\pm z_{\alpha /2}(\sigma /\sqrt{n})\) puede usar para construir un intervalo de\(100(1-\alpha )\%\) confianza para\(\mu\).
Si se desconoce la desviación estándar de la población y el tamaño de la muestra\(n\) es pequeño entonces cuando sustituimos la desviación estándar de\(\sigma\) la muestra\(s\) por la aproximación normal ya no es válida. La solución es utilizar una distribución diferente, llamada Student\(t\) -distribution con\(n-1\) grados de libertad. La\(t\) distribución de Student es muy parecida a la distribución normal estándar en que está centrada en\(0\) y tiene la misma forma cualitativa de campana, pero tiene colas más pesadas que la distribución normal estándar, como lo indica la Figura\(\PageIndex{1}\), en la que la curva (en marrón) que cumple con el línea vertical discontinua en el punto más bajo es la\(t\) distribución -con dos grados de libertad, la siguiente curva (en azul) es la\(t\) -distribución con cinco grados de libertad, y la curva delgada (en rojo) es la distribución normal estándar. Como también lo indica la figura, a medida que\(n\) aumenta el tamaño de la muestra, la\(t\) distribución de Student se asemeja cada vez más a la distribución normal estándar. Aunque hay una\(t\) distribución diferente para cada valor de\(n\), una vez que el tamaño de la muestra es\(30\) o más, normalmente es aceptable usar la distribución normal estándar en su lugar, como siempre haremos en este texto.
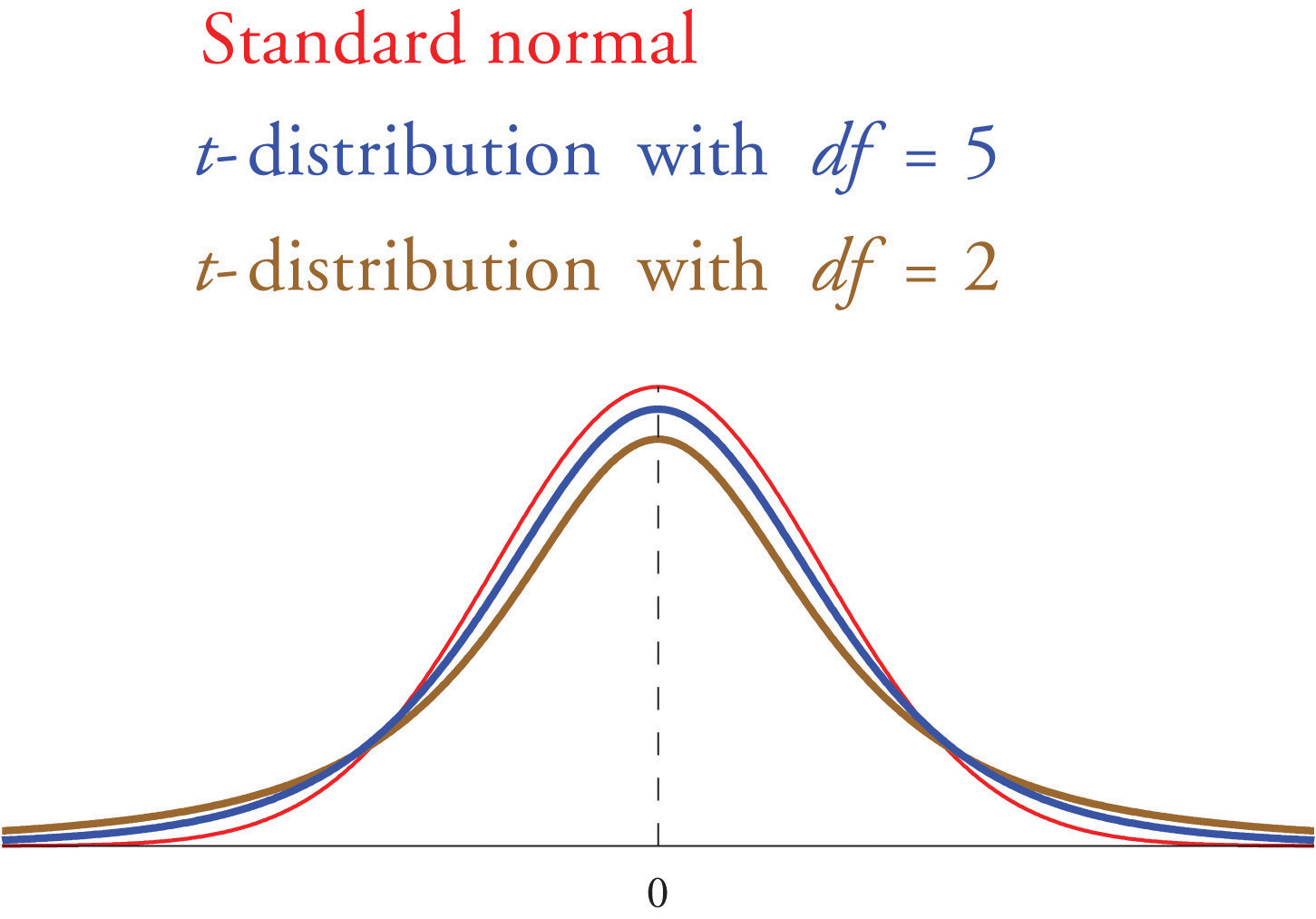
Así como el símbolo\(z_c\) representa el valor que corta una cola derecha del área\(c\) en la distribución normal estándar, así el símbolo\(t_c\) representa el valor que corta una cola derecha del área\(c\) en la distribución normal estándar. Esto nos da las siguientes fórmulas de intervalo de confianza.
Muestra pequeña\( 100(1−α)\%\) Confidence Interval for a Population Mean
Si\(σ\) se conoce:
\[\overline{x} = ±z_{α/2} \left( \dfrac{σ}{\sqrt{n}}\right) \]
Si\(σ\) se desconoce:
\[\overline{x} = ±t_{α/2} \left( \dfrac{s}{\sqrt{n}}\right) \label{tdist}\]
con los grados de libertad\( df=n−1\).
La población debe estar normalmente distribuida y una muestra se considera pequeña cuando\(n < 30\).
Para utilizar la nueva fórmula utilizamos la línea de la Figura 7.1.6 que corresponde al tamaño de muestra relevante.
Ejemplo\(\PageIndex{1}\)
Una muestra de tamaño\(15\) extraída de una población normalmente distribuida tiene media muestral\(35\) y desviación estándar de la muestra\(14\). Construir un intervalo de\(95\%\) confianza para la media poblacional e interpretar su significado.
Solución:
Dado que la población se distribuye normalmente, la muestra es pequeña, y se desconoce la desviación estándar de la población, la fórmula que aplica es la Ecuación\ ref {tdist}.
Nivel de confianza\(95\%\) significa que
\[α=1−0.95=0.05\]
así\(α/2=0.025\). Dado que el tamaño de la muestra es\(n = 15\), hay\(n−1=14\) grados de libertad. Por la Figura 7.1.6\(t_{0.025}=2.145\). Así
\[\begin{align} \overline{x} &= ±t_{α/2} \left( \dfrac{s}{\sqrt{n}}\right) \\ &=35 ± 2.145 \left( \dfrac{14}{\sqrt{15}} \right) \\ &=35 ±7.8 \end{align} \]
Uno puede estar\(95\%\) seguro de que el verdadero valor de\(μ\) está contenido en el intervalo
\[(35−7.8, 35+7.8) = (27.2,42.8).\]
Ejemplo\(\PageIndex{2}\)
Una muestra aleatoria de\(12\) estudiantes de una universidad grande produce promedio de GPA\(2.71\) con desviación estándar de la muestra\(0.51\). Construir un intervalo de\(90\%\) confianza para el promedio promedio de todos los estudiantes de la universidad. Supongamos que la población numérica de GPA de la que se toma la muestra tiene una distribución normal.
Solución:
Dado que la población se distribuye normalmente, la muestra es pequeña y se desconoce la desviación estándar de la población, la fórmula que aplica es Ecuación\ ref {tdist}
Nivel de confianza\(90\%\) significa que
\[α=1−0.90=0.10\]
así\(α/2=0.05\). Dado que el tamaño de la muestra es\(n = 12\), hay\(n−1=11\) grados de libertad. Por la Figura 7.1.6\(t_{0.05}=1.796\). Así
\[\begin{align} \overline{x} &= ±t_{α/2} \left( \dfrac{s}{\sqrt{n}}\right) \\ &=2.71 ± 1.796 \left( \dfrac{0.51}{\sqrt{12}} \right) \\ &=2.71 ±0.26 \end{align} \]
Uno puede estar\(90\%\) seguro de que el verdadero promedio promedio de todos los estudiantes de la universidad está contenido en el intervalo
\[(2.71−0.26,2.71+0.26)=(2.45,2.97).\]
Compare “Ejemplo 4" en la Sección 7.1 y “Ejemplo 6" en la Sección 7.1. Los estadísticos resumidos en las dos muestras son los mismos, pero el intervalo de\(90\%\) confianza para el GPA promedio de todos los estudiantes de la universidad en “Ejemplo 4" en la Sección 7.1,\((2.63,2.79)\), es más corto que el intervalo de\(90\%\) confianza\((2.45,2.97)\), en “Ejemplo 6" en la Sección 7.1. Esto se debe en parte a que en “Ejemplo 4" en la Sección 7.1 el tamaño de la muestra es mayor; hay más información perteneciente al valor verdadero de\(\mu\) en el conjunto de datos grande que en el pequeño.
Llave para llevar
- Al seleccionar la fórmula correcta para la construcción de un intervalo de confianza para una población media haga dos preguntas: ¿se\(\sigma\) conoce o desconoce la desviación estándar poblacional, y la muestra es grande o pequeña?
- Podemos construir intervalos de confianza con muestras pequeñas solo si la población es normal.

