4.4: Normalidad

¿Cómo decidir qué prueba usar, paramétrica o no paramétrica, prueba t o Wilcoxon? Necesitamos saber si la distribución sigue o al menos se acerca a la normalidad. Esto podría comprobarse visualmente (Figura\(\PageIndex{1}\)):

Código\(\PageIndex{1}\) (R):

salary <- c(21, 19, 27, 11, 102, 25, 21)
new.1000 <- sample((median(salary) - IQR(salary)) : + (median(salary) + IQR(salary)), 1000, replace=TRUE)
salary2 <- c(salary, new.1000)
qqnorm(salary2, main=""); qqline(salary2, col=2)

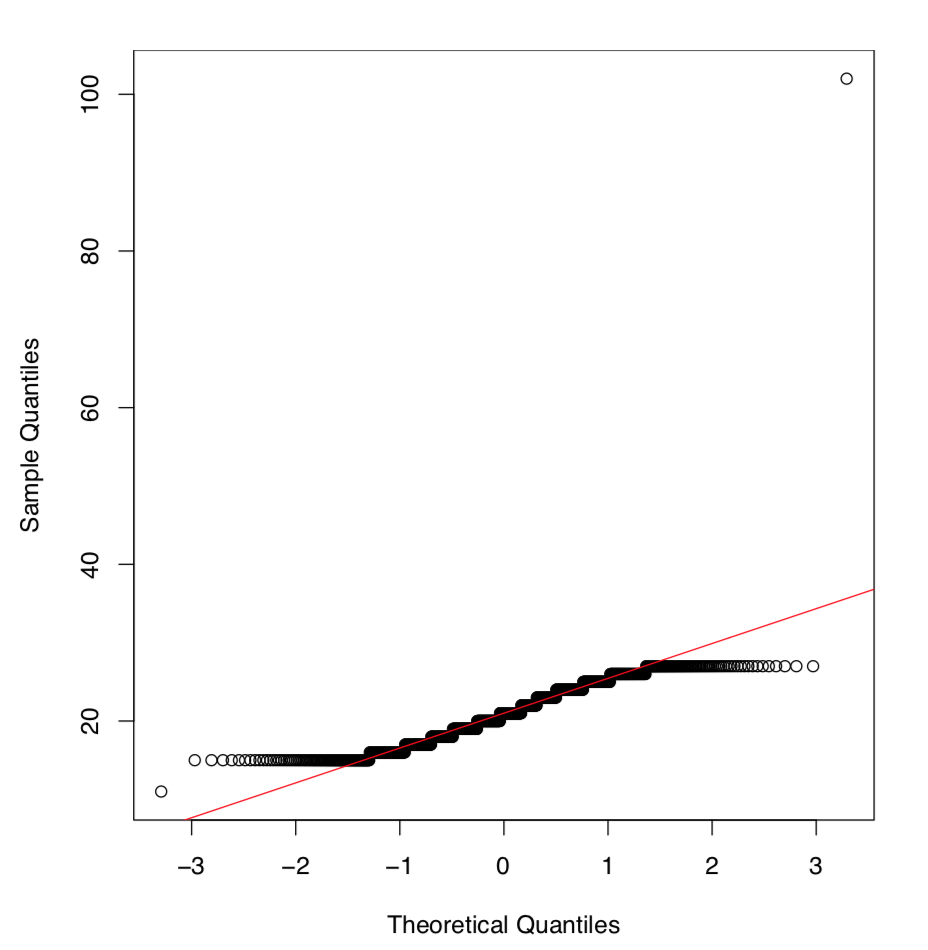
¿Cómo funciona la parcela QQ? Primero, se ordenan los puntos de datos y cada uno se asigna a un cuantil. En segundo lugar, se calcula un conjunto de cuantiles teóricos —posiciones que los puntos de datos deberían haber ocupado en una distribución normal —. Finalmente, se emparejan y trazan los cuantiles teóricos y empíricos.

Hemos superpuesto la parcela con una línea que viene a través de cuartiles. Cuando los puntos siguen la línea de cerca, la distribución empírica es normal. Aquí muchos puntos en la cola están lejos. Nuevamente, concluimos, que la distribución original no es normal.

R también ofrece instrumentos numéricos que verifican la normalidad. El primero de ellos es la prueba Shapiro-Wilk (por favor, ejecute este código usted mismo):

Código\(\PageIndex{2}\) (R):

salary <- c(21, 19, 27, 11, 102, 25, 21)
new.1000 <- sample((median(salary) - IQR(salary)) : + (median(salary) + IQR(salary)), 1000, replace=TRUE)
salary2 <- c(salary, new.1000)
shapiro.test(salary)
shapiro.test(salary2)

Aquí la salida es bastante concisa. Los valores P son pequeños, pero ¿cuál fue la hipótesis nula? Incluso la ayuda incorporada no lo indica. Para entender, podemos ejecutar un experimento simple:

Código\(\PageIndex{3}\) (R):

set.seed(1638) # freeze random number generator
shapiro.test(rnorm(100))

El comando rnorm () genera números aleatorios que siguen la distribución normal, tantos de ellos como se indica en el argumento. Aquí hemos obtenido un valor p acercándose a la unidad. Claramente, la hipótesis nula fue “la distribución empírica es normal”.

Figura Comprobación\(\PageIndex{1}\) gráfica de la normalidad.

Armados con este pequeño experimento, podemos concluir que las distribuciones tanto del salario como del salario2 no son normales.

La prueba Kolmogorov-Smirnov funciona con dos distribuciones. La hipótesis nula es que ambas muestras procedían de la misma población. Si queremos probar una distribución contra normal, el segundo argumento debería ser pnorm:

Código\(\PageIndex{4}\) (R):

salary <- c(21, 19, 27, 11, 102, 25, 21)
new.1000 <- sample((median(salary) - IQR(salary)) : + (median(salary) + IQR(salary)), 1000, replace=TRUE)
salary2 <- c(salary, new.1000)
ks.test(scale(salary2), "pnorm")

(El resultado es comparable con el resultado de la prueba Shapiro-Wilk. Escalamos los datos porque por defecto, el segundo argumento usa distribución normal escalada.)

La función ks.test () acepta cualquier tipo del segundo argumento y por lo tanto podría usarse para verificar qué tan confiable es aproximar la distribución de corriente con cualquier distribución teórica, no necesariamente normal. Sin embargo, la prueba de Kolmogorov-Smirnov suele devolver la respuesta incorrecta para las muestras de qué tamaño es\(< 50\), por lo que es menos potente que la prueba de Shapiro-Wilks.

2.2e-16 nos la llamada notación exponencial, la manera de mostrar números realmente pequeños como este (\(2.2 \times 10^{-16}\)). Si esta notación no te resulta cómoda, hay una manera de deshacerte de ella:

Código\(\PageIndex{5}\) (R):

salary <- c(21, 19, 27, 11, 102, 25, 21)
new.1000 <- sample((median(salary) - IQR(salary)) : + (median(salary) + IQR(salary)), 1000, replace=TRUE)
salary2 <- c(salary, new.1000)
old.options <- options(scipen=100)
ks.test(scale(salary2), "pnorm")
options(old.options)

(Opción scipen es igual al número máximo permitido de ceros.)

La mayoría de las veces estas tres formas de determinar la normalidad están de acuerdo, pero esto no es una sorpresa si devuelven resultados diferentes. El control de normalidad no es una sentencia de muerte, es solo una opinión basada en la probabilidad.

Nuevamente, si el tamaño de la muestra es pequeño, las pruebas estadísticas e incluso las parcelas cuantificables frecuentemente no logran detectar la no normalidad. En estos casos, herramientas más simples como la gráfica de tallo o el histograma, proporcionarían una mejor ayuda.