4.3: Intervalos de confianza

Última actualización
Guardar como PDF

Page ID: 150102

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Ya estamos listos para dar el primer paso en el mundo de las estadísticas inferenciales y utilizar pruebas estadísticas. Se inventaron para resolver la cuestión principal del análisis estadístico (Figura\(\PageIndex{1}\)): ¿cómo estimar algo sobre la población utilizando solo su muestra? Esto suena como una magia. ¿Cómo estimar a toda la población si no sabemos nada al respecto? Sin embargo, es posible si conocemos alguna ley de datos, característica que nuestra población debe seguir. Por ejemplo, la población podría exhibir una distribución de datos estándar.

Screen Shot 2019-01-09 a las 9.52.51 PM.png — Figura Representación\(\PageIndex{1}\) gráfica de la principal pregunta estadística: ¿cómo estimar la población (azul) a partir de la muestra (roja)? Flecha roja se relaciona con el intervalo de confianza. Para responder a la pregunta “gran roja”, se necesita el valor p.

Primero vamos a calcular el intervalo de confianza. Este intervalo predice con una probabilidad dada (generalmente 95%) donde la tendencia central particular (media o mediana) se ubica dentro de la población. No lo mezcles con los cuantiles del 95%, estas medidas tienen una naturaleza diferente.

Partimos de verificar la hipótesis de que la media poblacional es igual a 0. Esta es nuestra hipótesis nula, H\(_0\), que deseamos aceptar o rechazar con base en los resultados de las pruebas.

Código\(\PageIndex{1}\) (R):

t.test(trees$Height)

Aquí se utilizó una variante de prueba t para datos univariados que a su vez utiliza la distribución t estándar de Student. En primer lugar, esta prueba obtiene un estadístico específico del conjunto de datos original, el llamado estadístico t. El estadístico de prueba es una sola medida de algún atributo de una muestra; reduce todos los datos a un valor y con ayuda de distribución estándar, permite recrear la “población virtual”.

La prueba de estudiante viene con algún precio: debes asumir que tu población es “paramétrica”, “normal”, es decir, interpretable con una distribución normal (distribución del juego de dardos, ver el glosario).

En segundo lugar, esta prueba estima si la estadística derivada de nuestros datos puede provenir razonablemente de la distribución definida por nuestra suposición original. Este principio se encuentra en el corazón del cálculo del valor p. Esta última es la probabilidad de obtener nuestro estadístico de prueba si la suposición inicial, hipótesis nula era verdadera (en el caso anterior, la altura media del árbol es igual a 0).

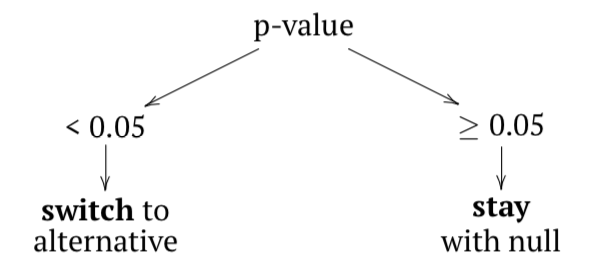
¿Qué vemos en la salida de la prueba? estadístico t es igual a 66.41 a 30 grados de libertad (df\(=30\)). El valor P es realmente bajo (\(2.2\times e^{-16}\)), casi cero, y definitivamente mucho más bajo que el nivel de confianza “sagrado” de 0.05.

Por lo tanto, rechazamos la hipótesis nula, o nuestra suposición inicial de que la altura media del árbol es igual a 0 y consecuentemente, vamos con la hipótesis alternativa que es un opuesto lógico de nuestra suposición inicial (es decir, “la altura no es igual a 0”):

Sin embargo, lo que es realmente importante en este momento, es el intervalo de confianza, un rango en el que la verdadera media poblacional debería caer con una probabilidad dada (95%). Aquí es estrecho, abarcando de 73.7 a 78.3 y no incluye cero. El último significa de nuevo que la hipótesis nula no es apoyada.

Screen Shot 2019-01-09 a las 9.55.36 PM.png

Si tus datos no van bien con la distribución normal, necesitas una prueba de suma de rangos de Wilcoxon más universal (pero menos potente). Utiliza la mediana en lugar de la media para calcular el estadístico de prueba V. Nuestra hipótesis nula será que la mediana de la población es igual a cero:

Código\(\PageIndex{2}\) (R):

salary <- c(21, 19, 27, 11, 102, 25, 21)
wilcox.test(salary, conf.int=TRUE)

(Por favor, ignore los mensajes de advertencia, simplemente dicen que nuestros datos tienen vínculos: dos salarios son idénticos).

Aquí también rechazaremos nuestra hipótesis nula con un alto grado de certeza. Al pasar un argumento conf.int=true se devolverá el intervalo de confianza para la mediana población—es amplio (porque el tamaño de la muestra es pequeño) pero no incluye cero.