5.2: ¿Hay alguna diferencia? Comparando dos muestras

Pruebas de dos muestras

Al estudiar dos muestras, utilizamos el mismo enfoque con dos hipótesis. La hipótesis nula típica es “no hay diferencia entre estas dos muestras”, es decir, ambas se extraen de la misma población. La hipótesis alternativa es que “hay una diferencia entre estas dos muestras”. Hay muchas otras formas de decir que:

• Nulo: diferencia igual a 0\(\approx\) muestras muestras similares\(\approx\)\(\approx\) muestras relacionadas provinieron de la misma población
• Alternativa: diferencia no igual a 0\(\approx\) muestras muestras diferentes\(\approx\) muestras no relacionadas\(\approx\) provinieron de diferentes poblaciones

Y, en términos de valor p:

Si los datos son “paramétricos”, entonces se requiere una prueba t paramétrica. Si las variables que queremos comparar se obtuvieron en diferentes objetos, usaremos una prueba t de dos muestras para variables independientes, que se llama con el comando t.test ():

Código\(\PageIndex{1}\) (R):

bpress <- read.table("data/bpress.txt", h=TRUE)
head(bpress)
drug.d <- bpress$DRUG.10 - bpress$DRUG.1
placebo.d <- bpress$PLACEBO.10 - bpress$PLACEBO.1
sapply(data.frame(placebo.d, drug.d), Normality) # asmisc.r
Normality <- function(a) {ifelse(shapiro.test(a)$p.value < 0.05, "NOT NORMAL", "NORMAL")}
t.test(placebo.d, drug.d)

Hay una salida larga. Tenga en cuenta lo siguiente:

• Aparte de la normalidad, existe una segunda suposición de la prueba t clásica, homogeneidad de varianzas. Sin embargo, R por defecto realiza una prueba de Welch más complicada que no requiere homogeneidad. Es por ello que los grados de libertad no son un número entero.
• t es un estadístico t y df son grados de libertad (relacionados con el número de casos), ambos necesitaban para calcular el valor p.
• El intervalo de confianza es la segunda salida más importante de la R t.test (). Se recomienda suministrar intervalos de confianza y tamaños de efecto (ver abajo) siempre que sea posible. Si cero está dentro del intervalo de confianza, hay una diferencia.
• el valor p es pequeño, por lo tanto la probabilidad de “levantar la falsa alarma” cuando “no pasa nada” también es pequeña. En consecuencia, rechazamos la hipótesis nula (“no pasa nada”, “no hay diferencia”, “ningún efecto”) y por lo tanto cambiamos a la hipótesis alternativa (“hay diferencia entre drogas”).

Podemos usar el siguiente orden de lo más a lo menos importante:

1. el valor p es primero porque ayuda a tomar decisiones;
2. intervalo de confianza;
3. t estadística;
4. grados de libertad.

Los resultados de la prueba t no salieron de la nada. Calculemos lo mismo manualmente (en realidad, medio manualmente porque usaremos grados de libertad a partir de los resultados de las pruebas anteriores):

Código\(\PageIndex{2}\) (R):

bpress <- read.table("data/bpress.txt", h=TRUE)
drug.d <- bpress$DRUG.10 - bpress$DRUG.1
placebo.d <- bpress$PLACEBO.10 - bpress$PLACEBO.1
df <- 6.7586
v1 <- var(placebo.d)
v2 <- var(drug.d)
(t.stat <- (mean(placebo.d) - mean(drug.d))/sqrt(v1/5 + v2/5))
(p.value <- 2*pt(-abs(t.stat), df))

(La función pt () calcula los valores de la distribución Student, la que se utiliza para la prueba t. En realidad, en lugar del cálculo directo, esta y otras funciones similares estiman los valores p utilizando tablas y fórmulas aproximadas. Esto se debe a que el cálculo directo de la probabilidad exacta requiere integración, determinando el cuadrado bajo la curva, como\(\alpha\) a partir de la Figura 5.1.1.)

Usando el estadístico t y grados de libertad, se puede calcular el valor p sin ejecutar la prueba. Es por ello que para reportar el resultado de la prueba t (y la prueba de Wilcoxon relacionada, ver más adelante), la mayoría de los investigadores listan estadística, grados de libertad (solo para prueba t) y valor p.

En lugar de “forma corta” desde arriba, puede usar un “formulario largo” cuando la primera columna del marco de datos contiene todos los datos, y la segunda indica grupos:

Código\(\PageIndex{3}\) (R):

bpress <- read.table("data/bpress.txt", h=TRUE)
drug.d <- bpress$DRUG.10 - bpress$DRUG.1
placebo.d <- bpress$PLACEBO.10 - bpress$PLACEBO.1
long <- stack(data.frame(placebo.d, drug.d))
head(long)
t.test(values ~ ind, data=long)

(Tenga en cuenta la interfaz de fórmula que generalmente se junta con una forma larga).

La forma larga es útil también para trazar y manipulaciones de datos (verifique la trama usted mismo):

Código\(\PageIndex{4}\) (R):

bpress <- read.table("data/bpress.txt", h=TRUE)
drug.d <- bpress$DRUG.10 - bpress$DRUG.1
placebo.d <- bpress$PLACEBO.10 - bpress$PLACEBO.1
long <- stack(data.frame(placebo.d, drug.d))
boxplot(values ~ ind, data=long)
tapply(long$values, long$ind, sd)
aggregate(values ~ ind, range, data=long)

Otro ejemplo de forma larga son los datos incrustados de castero2:

Código\(\PageIndex{5}\) (R):

Normality <- function(a) {ifelse(shapiro.test(a)$p.value < 0.05, "NOT NORMAL", "NORMAL")}
tapply(beaver2$temp, beaver2$activ, Normality) # asmisc.r
boxplot(temp ~ activ, data=beaver2)
t.test(temp ~ activ, data=beaver2)

(Marque la parcela de caja usted mismo. Supusimos que la temperatura se midió aleatoriamente).

Nuevamente, el valor p es mucho menor que 0.05, y debemos rechazar la hipótesis nula de que las temperaturas no son diferentes cuando el castor está activo o no.

Para convertir la forma larga en corta, utilice la función unstack ():

Código\(\PageIndex{6}\) (R):

uu <- unstack(beaver2, temp ~ activ)
str(uu)

(Tenga en cuenta que el resultado es una lista porque los números de observaciones para castor activo e inactivo son diferentes. Esta es otra ventaja de la forma larga: puede manejar subconjuntos de tamaño desigual).

Si se obtuvieron mediciones en un objeto, se debe usar una prueba t pareada. De hecho, es solo una prueba t de una muestra aplicada a las diferencias entre cada par de mediciones. Para hacer la prueba t pareada en R, utilice el parámetro Paired=True. No es ilegal elegir la prueba t común para los datos emparejados, pero las pruebas emparejadas suelen ser más potentes:

Código\(\PageIndex{7}\) (R):

bpress <- read.table("data/bpress.txt", h=TRUE)
drug.d <- bpress$DRUG.10 - bpress$DRUG.1
placebo.d <- bpress$PLACEBO.10 - bpress$PLACEBO.1
sapply(bpress, Normality) # asmisc.r
Normality <- function(a) {ifelse(shapiro.test(a)$p.value < 0.05, "NOT NORMAL", "NORMAL")}
attach(bpress)
t.test(DRUG.1, DRUG.10, paired=TRUE)
t.test(DRUG.10 - DRUG.1, mu=0) # same results
t.test(DRUG.1, DRUG.10) # non-paired
detach(bpress)

Si el caso de las mediciones de presión arterial, la prueba t común no “sabe” qué factor es más responsable de las diferencias: influencia farmacológica o variación individual entre las personas. La prueba t pareada excluye la variación individual y permite que cada persona sirva como su propio control, por eso es más precisa.

También más precisas (si la hipótesis alternativa se especifica correctamente) son las pruebas de una cola:

Código\(\PageIndex{8}\) (R):

bpress <- read.table("data/bpress.txt", h=TRUE)
drug.d <- bpress$DRUG.10 - bpress$DRUG.1
placebo.d <- bpress$PLACEBO.10 - bpress$PLACEBO.1
attach(bpress)
t.test(PLACEBO.10, DRUG.10, alt="greater") # one-tailed test
t.test(PLACEBO.10, DRUG.10) # "common" test
detach(bpress)

(Aquí se utilizó otra hipótesis alternativa: en lugar de adivinar la diferencia, adivinamos que la presión arterial en el grupo “placebo” era mayor el día 10.)

Nota muy importante: todas las decisiones relacionadas con las pruebas estadísticas (paramétricas o no paramétricas, pareadas o no pareadas, unilaterales o bilaterales, 0.05 o 0.01) deben hacerse a priori, antes del análisis. ¡La “caza del valor p” es ilegal!

Si trabajamos con datos no paramétricos, se requiere una prueba no paramétrica de Wilcoxon (también conocida como prueba de Mann-Whitney), bajo el comando wilcox.test ():

Código\(\PageIndex{9}\) (R):

Normality <- function(a) {ifelse(shapiro.test(a)$p.value < 0.05, "NOT NORMAL", "NORMAL")}
tapply(ToothGrowth$len, ToothGrowth$supp, Normality) # asmisc.r
boxplot(len ~ supp, data=ToothGrowth, notch=TRUE)
wilcox.test(len ~ supp, data=ToothGrowth)

(Por favor, ejecute el código boxplot y tenga en cuenta el uso de muescas. Se acepta comúnmente que las muescas superpuestas son un signo de no diferencia. Y sí, la prueba de Wilcoxon lo respalda. Las muescas no son predeterminadas porque en muchos casos, las gráficas de caja no se superponen visualmente. Por cierto, asumimos aquí que solo la variable supp está presente y se ignora la dosis (¿ve? Crecimiento de dientes para más detalles).)

Y sí, es realmente tentador concluir algo excepto “quedarse con nulo” si el valor p es 0.06 (Figura\(\PageIndex{1}\)) pero no. Esto no está permitido.

Al igual que en la prueba t, los datos emparejados requieren el parámetro paired=true:

Código\(\PageIndex{10}\) (R):

Normality <- function(a) {ifelse(shapiro.test(a)$p.value < 0.05, "NOT NORMAL", "NORMAL")}
w0 <- ChickWeight$weight[ChickWeight$Time == 0]
w2 <- ChickWeight$weight[ChickWeight$Time == 2]
sapply(data.frame(w0, w2), Normality)
boxplot(w0, w2)
wilcox.test(w0, w2, paired=TRUE)

(¡Los pesos de pollo son realmente diferentes entre la eclosión y el segundo día! Por favor, marque la caja usted mismo.)

Figura\(\PageIndex{1}\) Cómo no interpretar los valores p (tomado de XKCD, https://xkcd.com/1478/)

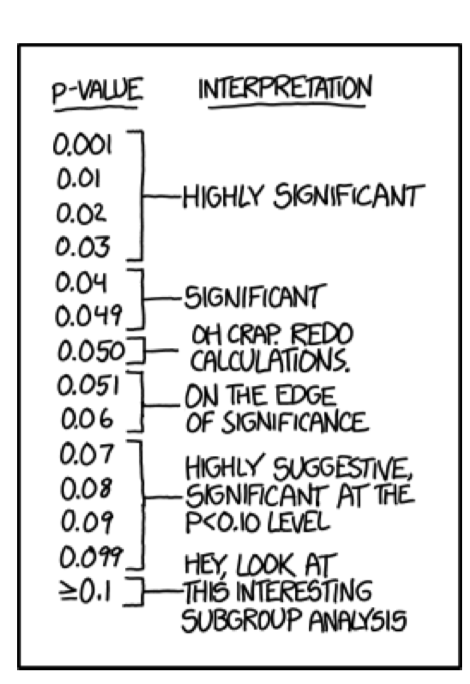
Las pruebas no paramétricas son generalmente más universales ya que no asumen ninguna distribución en particular. Sin embargo, son menos potentes (propensos al error Tipo II, “descuido”). Además, las pruebas no paramétricas basadas en rangos (como la prueba de Wilcoxon) son sensibles a la heterogeneidad de las varianzas\(^{[1]}\). Con todo, las pruebas paramétricas son preferibles cuando los datos cumplen con sus supuestos. Tabla\(\PageIndex{1}\) resume este sencillo procedimiento.

Cuadro\(\PageIndex{1}\): Cómo elegir prueba de dos muestras en R. Esta tabla debe leerse desde la celda superior derecha.

	Pareado: un objeto, dos medidas	No emparejado
Normal	t.test (..., Paired=True)	t.test (...)
No normal	wilcox.test (..., Paired=True)	wilcox.test (...)

Incrustado en R se encuentra el clásico conjunto de datos utilizado en la obra original de Student (el seudónimo del matemático William Sealy Gossett que trabajaba para la cervecería Guinness y no se le permitió usar su nombre real para publicaciones). Este trabajo se ocupó de comparar los efectos de dos fármacos sobre la duración del sueño para 10 pacientes.

En R estos datos están disponibles bajo el nombre sleep (La figura\(\PageIndex{2}\) muestra las gráficas de caja correspondientes). Los datos están en forma larga: columna extra contiene el incremento de los tiempos de sueño (en horas, positivas o negativas) mientras que el grupo de columnas indica el grupo (tipo de fármaco).

Código\(\PageIndex{11}\) (R):

plot(extra ~ group, data=sleep)

Figura\(\PageIndex{2}\) El incremento promedio del sueño con dos drogas.

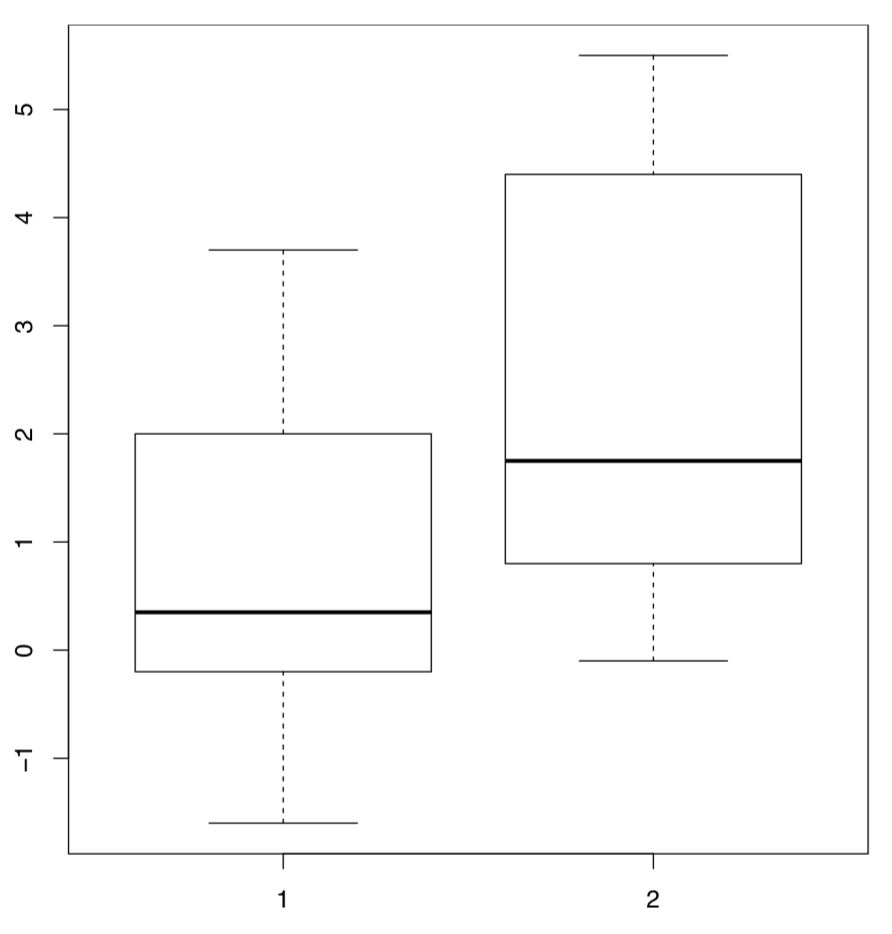
(El trazado usa la “fórmula del modelo”: en este caso, el grupo ~ extra. R es lo suficientemente inteligente como para entender que el grupo es el factor de “división” y debe usarse para hacer dos parcelas de caja).

El efecto de cada fármaco en cada persona es individual, pero la duración promedio por la cual el medicamento prolonga el sueño puede considerarse una representación razonable de la “fuerza” de la droga. Con esta suposición, intentaremos utilizar una prueba de dos muestras para determinar si existe una diferencia significativa entre las medias de las dos muestras correspondientes a los dos fármacos. Primero, necesitamos determinar qué prueba usar:

Código\(\PageIndex{12}\) (R):

Normality <- function(a) {ifelse(shapiro.test(a)$p.value < 0.05, "NOT NORMAL", "NORMAL")}
tapply(sleep$extra, sleep$group, Normality) # asmisc.r

(Los datos en la forma larga son perfectamente adecuados para tapply () que divide el primer argumento de acuerdo con el segundo, y luego aplica el tercer argumento a todos los subconjuntos.)

Dado que los datos cumplen con el supuesto de normalidad, ahora podemos emplear la prueba t paramétrica pareada:

Código\(\PageIndex{13}\) (R):

t.test(extra ~ group, data=sleep, paired=TRUE)

(Sí, deberíamos rechazar hipótesis nulas sobre ninguna diferencia.)

¿Qué tal la probabilidad de errores Tipo II (falsos negativos)? Se relaciona con la potencia estadística, y podría calcularse mediante prueba de potencia:

Código\(\PageIndex{14}\) (R):

power.t.test(n=10, sig.level=0.05, d=1.58)

Por lo tanto, si queremos el nivel de significancia 0.05, tamaño de muestra 10 y el efecto (diferencia entre medias) 1.58, entonces la probabilidad de falsos negativos debe ser aproximadamente\(1-0.92=0.08\) que es realmente baja. En conjunto, esto hace que cerca del 100% nuestro valor predictivo positivo (VPP), probabilidad de que nuestro resultado positivo (diferencia observada) sea verdaderamente positivo para toda la población estadística. El caret del paquete es capaz de calcular PPV y otros valores relacionados con la potencia estadística.

A veces se dice que la prueba t puede manejar el número de muestras tan bajo como apenas cuatro. Esto no es del todo correcto ya que el poder está sufriendo de pequeños tamaños de muestra, pero es cierto que la razón principal para inventar la prueba t fue trabajar con muestras pequeñas, más pequeñas entonces “regla de 30” discutidas en primer capítulo.

Tanto la prueba t como la prueba de Wilcoxon comprueban diferencias solo entre medidas de tendencia central (por ejemplo, medias). Estas muestras homogéneas

Código\(\PageIndex{15}\) (R):

(aa <- 1:9)
(bb <- rep(5, 9))

tener la misma media pero diferentes varianzas (compruébalo tú mismo), y así la diferencia no se detectaría con la prueba t o la prueba de Wilcoxon. Por supuesto, también existen pruebas para medidas de escala (como var.test ()), y pueden encontrar la diferencia. Podrías probarlos tú mismo. La tercera muestra homogénea complementa el caso:

Código\(\PageIndex{16}\) (R):

(xx <- 51:59)

ya que ahora se detectarán diferencias en centros, no en rangos (verifíquelo).

Hay muchas otras dos pruebas de muestra. Una de ellas, la prueba de signos, es tan sencilla que no existe en R por defecto. La prueba de signos primero calcula las diferencias entre cada par de elementos en dos muestras de igual tamaño (es una prueba pareada). Entonces, considera sólo los valores positivos y hace caso omiso de los demás. La idea es que si se tomaran muestras de la misma distribución, entonces aproximadamente la mitad de las diferencias deberían ser positivas, y la prueba de proporciones no encontrará una diferencia significativa entre 50% y la proporción de diferencias positivas. Si las muestras son diferentes, entonces la proporción de diferencias positivas debe ser significativamente mayor o menor a la mitad.

Llegar con el código R para realizar la prueba de señal, y probar dos muestras que se mencionaron al inicio de la sección.

El conjunto de datos estándar de calidad del aire contiene información sobre la cantidad de ozono en la atmósfera alrededor de la ciudad de Nueva York de mayo a septiembre de 1973. La concentración de ozono se presenta como una media redondeada para cada día. Para analizarlo de manera conservadora, utilizamos métodos no paramétricos.

Determinar qué tan cerca de la distribución normal están las mediciones de concentración mensuales.

Probemos la hipótesis de que los niveles de ozono en mayo y agosto fueron los mismos:

Código\(\PageIndex{17}\) (R):

wilcox.test(Ozone ~ Month, data=airquality, subset = Month %in% c(5, 8), conf.int=TRUE)

(Dado que Mes es una variable discreta ya que el “número” simplemente representa el mes, los valores de Ozono se agruparán por mes. Se utilizó el subconjunto de parámetros con el operador %en%, que elige mayo y agosto, el mes 5 y 8. Para obtener el intervalo de confianza, se utilizó el parámetro adicional conf.int. \(W\)es el estadístico empleado en el cálculo de los valores p. Finalmente, hubo mensajes de advertencia sobre vínculos que ignoramos.)

La prueba rechaza la hipótesis nula, de igualdad entre la distribución de las concentraciones de ozono en mayo y agosto, con bastante confianza. Esto es plausible porque el nivel de ozono en la atmósfera depende fuertemente de la actividad solar, la temperatura y el viento.

Las diferencias entre muestras están bien representadas por diagramas de caja (Figura\(\PageIndex{3}\)):

Código\(\PageIndex{18}\) (R):

boxplot(Ozone ~ Month, data=airquality, subset=Month %in% c(5, 8), notch=TRUE)

Figura\(\PageIndex{3}\) Distribución del ozono en mayo y junio.

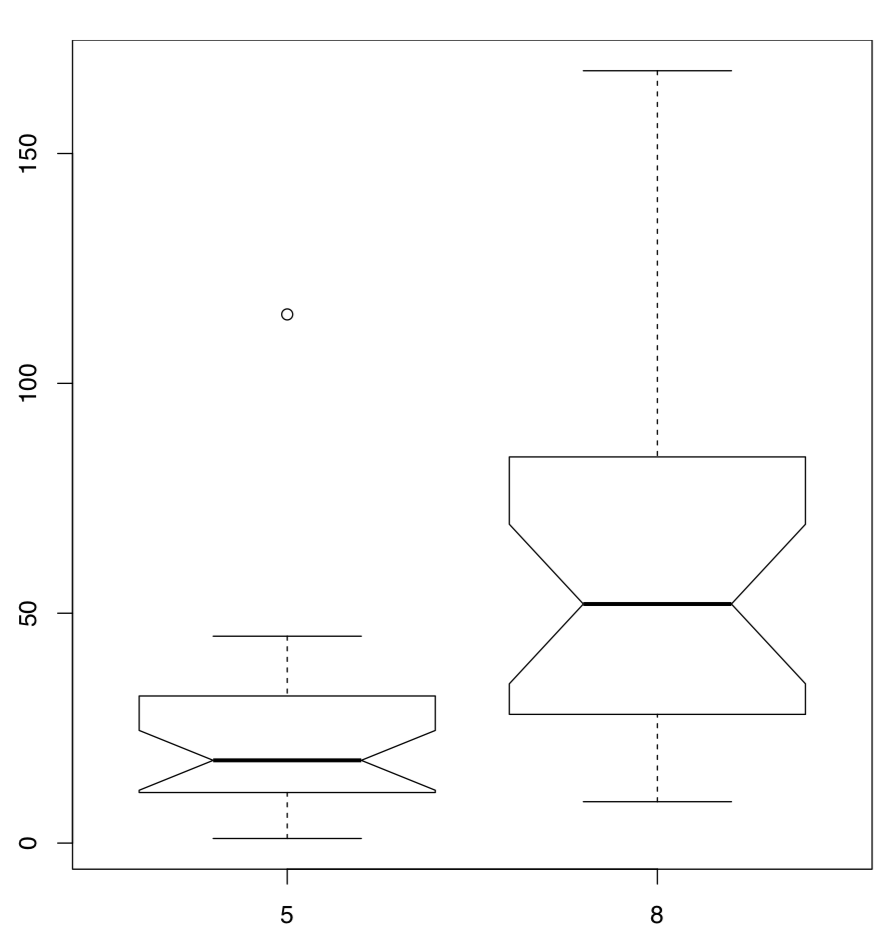
(Tenga en cuenta que en el comando boxplot () usamos la misma fórmula que el modelo estadístico. El subconjunto de opciones es una forma alternativa de seleccionar del marco de datos.)

Se considera convencionalmente que si las cajas se superponen en más de un tercio de su longitud, las muestras no son significativamente diferentes.

El último ejemplo de esta sección está relacionado con el descubrimiento del argón. Al principio, no se entendía que los gases inertes existen en la naturaleza ya que son realmente difíciles de descubrir químicamente. Pero a finales del siglo XIX empiezan a acumularse datos de que algo anda mal con el gas nitrógeno (N\(_2\)). El físico Lord Rayleigh presentó datos que muestran que las densidades del gas nitrógeno producido a partir del amoníaco y el gas nitrógeno producido a partir del aire son diferentes:

Código\(\PageIndex{19}\) (R):

ar <- read.table("data/argon.txt")
unstack(ar, form=V2 ~ V1)

Como se puede ver, la diferencia es realmente pequeña. No obstante, bastó para que el químico Sir William Ramsay lo aceptara como un reto. Ambos científicos realizaron series de experimentos avanzados que finalmente dieron como resultado el descubrimiento de nuevo gas, el argón. En 1904, recibieron dos premios Nobel, uno en ciencias físicas y otro en química. Desde el punto de vista estadístico, lo más llamativo es cómo funcionan los métodos de visualización con estos datos:

Código\(\PageIndex{20}\) (R):

ar <- read.table("data/argon.txt")
means <- tapply(ar$V2, ar$V1, mean, na.rm=TRUE)
oldpar <- par(mfrow=1:2)
boxplot(V2 ~ V1, data=ar)
barplot(means)
par(oldpar)

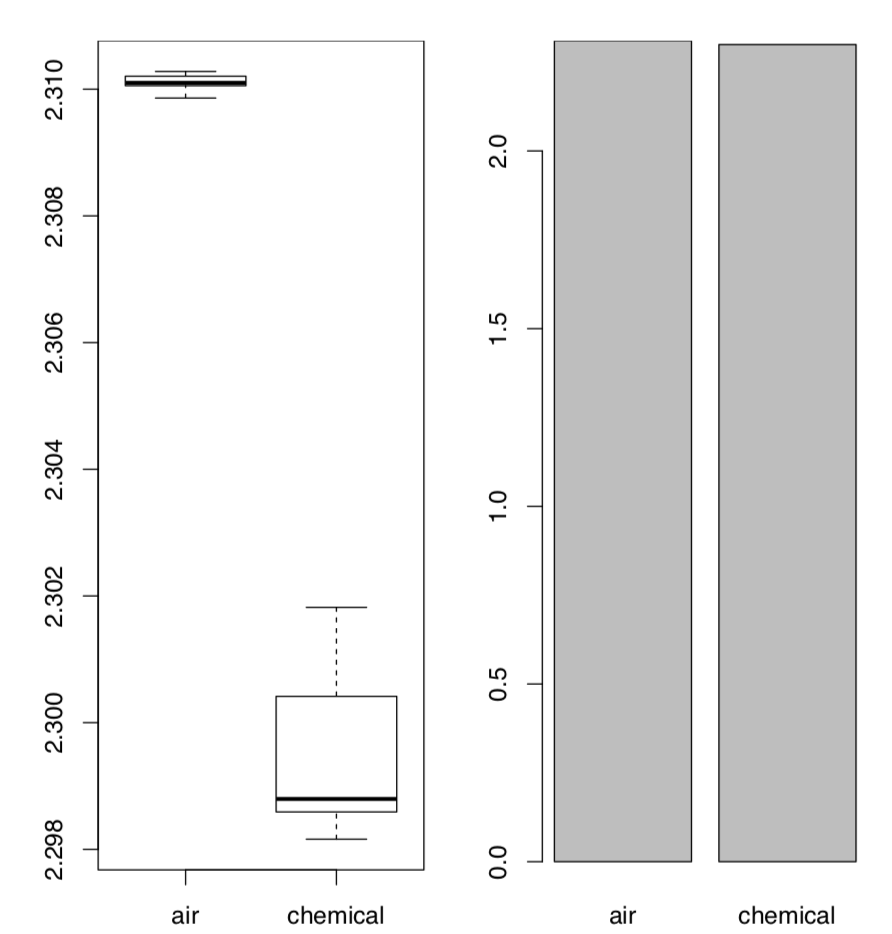
La Figura\(\PageIndex{4}\) muestra lo más claro posible que las gráficas de caja tienen una gran ventaja sobre las gráficas de barras tradicionales, especialmente en los casos de comparación de dos muestras.

Por lo tanto, recomendamos evitar las parcelas de barras, y por todos los medios evitar las llamadas “parcelas de dinamita” (parcelas de barras con barras de error en la parte superior). ¡Cuidado con la dinamita!

Sus desventajas más importantes son (1) esconden datos primarios (por lo que no son exploratorios), y al mismo tiempo, no ilustran ninguna prueba estadística (por lo que no son inferenciales); (2) ellos (frecuentemente erróneamente) asumen que los datos son simétricos y paramétricos; (3) utilizan el espacio ineficientemente, tienen datos bajos- relación a tinta; (4) provocan una ilusión óptica en la que el lector agrega parte de la barra de error a la altura de la barra principal al intentar juzgar las alturas de las barras principales; (5) la barra de error de desviación estándar (típica allí) no tiene relación directa incluso con comparar dos muestras (ver arriba cómo funciona la prueba t), y casi no tiene nada que ver con la comparación de múltiples muestras (ver a continuación cómo funciona el ANOVA). Y, por supuesto, no ayudan a Lord Rayleigh y Sir William Ramsay a recibir sus premios Nobel.

Figura\(\PageIndex{4}\) ¿Cuál de estas dos tramas ayudaría a Lord Rayleigh y Sir William Ramsay a recibir más sus Premios Nobel? (La idea de Tukey, 1977.)

Por favor revise los datos de Lord Rayleigh con la prueba estadística apropiada e informe los resultados.

Entonces, ¿qué hacer con las parcelas de dinamita? Reemplázalos con parcelas de caja. La única desventaja de las parcelas de caja es que son más difíciles de dibujar con la mano lo que suena gracioso en la era de las computadoras. Esto, por cierto, explica en parte por qué hay tanta dinamita alrededor: son una especie de tiempos preinformáticos heredados.

Un supermercado cuenta con dos cajeros. Para analizar su eficiencia laboral, la longitud de la línea en cada uno de sus registros se registra varias veces al día. Los datos se registran en kass.txt. ¿Qué cajero procesa a los clientes más rápidamente?

Tamaños de efecto

Las pruebas estadísticas permiten tomar decisiones pero no muestran cuán diferentes son las muestras. Considera los siguientes ejemplos:

Código\(\PageIndex{21}\) (R):

wilcox.test(1:10, 1:10 + 0.001, paired=TRUE)
wilcox.test(1:10, 1:10 + 0.0001, paired=TRUE)

(¡Aquí la diferencia disminuye pero el valor p no crece!)

Uno de los errores del principiante es pensar que los valores p miden las diferencias, pero esto es realmente incorrecto.

Los valores P son probabilidades y no se supone que midan nada. Podrían usarse solo de una manera, binaria, sí/no: para ayudar con las decisiones estadísticas.

Además, el investigador casi siempre puede obtener un valor p razonablemente bueno, aunque el efecto sea minúsculo, como en el segundo ejemplo anterior.

Para estimar el alcance de las diferencias entre poblaciones, se inventaron tamaños de efecto. Se recomienda encarecidamente que reporten junto con valores p.

Package effsize calcula varias métricas de tamaño de efecto y proporciona interpretaciones de su magnitud.

La d de Cohen es la métrica de tamaño del efecto paramétrico que indica diferencia entre dos medias:

Código\(\PageIndex{22}\) (R):

library(effsize)
cohen.d(extra ~ group, data=sleep)

(Tenga en cuenta que en el último ejemplo, el tamaño del efecto es grande con intervalo de confianza incluyendo cero; esto estropea el efecto “grande”).

Si los datos no son paramétricos, es mejor usar el Delta de Cliff:

Código\(\PageIndex{23}\) (R):

cliff.delta(1:10, 1:10+0.001)
cliff.delta(Ozone ~ Month, data=airquality, subset = Month %in% c(5, 8))

Ahora tenemos bastantes medidas para guardar en la memoria. La tabla simple a continuación enfatiza las más utilizadas:

	Centro	Escala	Test	Efecto
Paramétrico	Media	Desviación estándar	prueba t	D de Cohen
No paramétricos	Mediana	IQR, LOCO	Prueba de Wilcoxon	Delta del acantilado

Cuadro\(\PageIndex{2}\): Herramientas numéricas más utilizadas, tanto para una como para dos muestras.

Hay muchas medidas de tamaños de efecto. En biología, es útil el coeficiente de divergencia (\(K\)) descubierto por Alexander Lyubishchev en 1959, y relacionado con la diferencia de medias estrictamente estandarizada al cuadrado recientemente introducida (SSSMD):

Código\(\PageIndex{24}\) (R):

K(extra ~ group, data=sleep) # asmisc.r
summary(K(extra ~ group, data=sleep))

Lyubishchev señaló que las buenas especies biológicas deberían tener\(K>18\), esto significa que no hay transgresión.

El coeficiente de divergencia es robusto a los cambios alométricos:

Código\(\PageIndex{25}\) (R):

K(extra ~ group, data=sleep) # asmisc.r
(aa <- 1:9)
summary(K(aa*3, aa*10)) # asmisc.r
cliff.delta(1:10, 1:10+0.001)
cliff.delta(Ozone ~ Month, data=airquality, subset = Month %in% c(5, 8))
cliff.delta(aa*3, aa*10)

También hay una variante no paramétrica basada en MAD de\(K\):

Código\(\PageIndex{26}\) (R):

K(extra ~ group, data=sleep) # asmisc.r
summary(K(1:10, 1:10+0.001, mad=TRUE)) # asmisc.r
(dd <- K(Ozone ~ Month, data=airquality[airquality$Month %in% c(5, 8), ], mad=TRUE)) # asmisc.r
summary(dd)

En el archivo de datos grades.txt se encuentran las calificaciones de un grupo particular de alumnos para el primer examen (en la columna etiquetada A1) y el segundo examen (A2), así como las calificaciones de un segundo grupo de alumnos para el primer examen (B1). ¿Las calificaciones de la clase A para los exámenes primero y segundo son diferentes? ¿Qué clase le fue mejor en el primer examen, A o B? Reporta significancias, intervalos de confianza y tamaños de efecto.

En el repositorio abierto, el archivo aegopodium.txt contiene medidas de hojas de plantas de sol y sombra Aegopodium podagraria (saúco de tierra). Por favor, encuentre el carácter que es más diferente entre sol y sombra y aplique la prueba estadística adecuada para determinar si esta diferencia es significativa. Informar también el intervalo de confianza y el tamaño del efecto.

Referencias

1. Sin embargo, hay una solución alternativa, prueba de orden de rango robusta, busque la función RRO.test () en theasmisc.r.