5.3: Si hay más de dos muestras - ANOVA

De una manera

¿Y si necesitamos saber si hay diferencias entre tres muestras? La primera idea podría ser hacer la serie de pruebas estadísticas entre cada par de la muestra. En el caso de tres muestras, necesitaremos tres pruebas t o pruebas de Wilcoxon. Lo lamentable es que el número de pruebas requeridas crecerá dramáticamente con el número de muestras. Por ejemplo, ¡para comparar seis muestras necesitaremos realizar 15 pruebas!

Un problema aún más grave es que todas las pruebas se basan en la idea de probabilidad. En consecuencia, la posibilidad de hacer del error Tipo I (falsa alarma) crecerá cada vez que realicemos más pruebas simultáneas en la misma muestra.

Por ejemplo, en una prueba, si la hipótesis nula es cierta, generalmente solo hay un 5% de probabilidad de rechazarla por error. Sin embargo, con 20 pruebas (Figura E.2), si todas las hipótesis nulas correspondientes son verdaderas, ¡el número esperado de rechazos incorrectos es 1! A esto se le llama el problema de las comparaciones múltiples.

Uno de los ejemplos más llamativos de comparaciones múltiples es un “caso de salmón muerto”. En 2009, un grupo de investigaciones publicó los resultados de las pruebas de resonancia magnética que detectaron la actividad cerebral en un pez muerto. Pero eso fue simplemente porque a propósito no dieron cuenta de múltiples comparaciones\(^{[1]}\).

La técnica especial, Analysis Of Variance (ANOVA) se inventó para evitar comparaciones múltiples en el caso de más de dos muestras.

En el lenguaje de fórmulas R, ANOVA podría describirse como

factor de respuesta ~

donde respuesta es la variable de medición. Tenga en cuenta que la única diferencia con respecto al caso de dos muestras anterior es que el factor en ANOVA tiene más de dos niveles.

La hipótesis nula aquí es que todas las muestras pertenecen a una misma población (“no son diferentes”), y la hipótesis alternativa es que al menos una muestra es divergente, no pertenece a la misma población (“las muestras son diferentes”).

En términos de valores p:

La figura lo\(\PageIndex{1}\) explica sobre el ejemplo de múltiples muestras de manzana mezcladas con muestra divergente de jitomate.

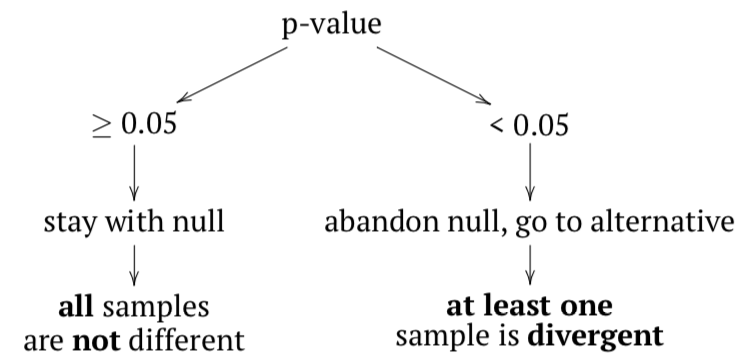
Si alguna muestra proviene de una población diferente, entonces la varianza entre muestras debe ser al menos comparable con (o mayor entonces) variación dentro de las muestras; en otras palabras, el valor F (o relación F) debe ser\(\geq 1\). Para comprobarlo inferencialmente, se aplica la prueba F. Si el valor p es lo suficientemente pequeño, entonces al menos una muestra (subconjunto, columna) es divergente.

El ANOVA no revela qué muestra es diferente. Esto se debe a que se agrupan las varianzas en el ANOVA. Pero, ¿y si aún necesitamos saber eso? Entonces deberíamos aplicar pruebas post hoc. No se requiere en ejecutarlos después del ANOVA; lo que se requiere es realizarlos con cuidado y aplicar siempre el ajuste del valor p para múltiples comparaciones. Este ajuste generalmente aumenta el valor p para evitar la acumulación de múltiples pruebas. ANOVA y pruebas post hoc responden a diferentes preguntas de investigación, por lo tanto, esto depende del investigador decidir cuál y cuándo realizar.

El ANOVA es un método paramétrico, y esto suele ir bien con su primer supuesto, la distribución normal de los residuos (desviaciones entre los valores observados y esperados). Normalmente, verificamos la normalidad de todo el conjunto de datos porque ANOVA usa datos agrupados de todos modos. También es posible verificar la normalidad de los residuos directamente (ver más abajo). Tenga en cuenta que el ANOVA tolera desviaciones leves de la normalidad, tanto en los datos como en los residuales. Pero si los datos son claramente no paramétricos, se recomienda utilizar otros métodos (ver más abajo).

Figura Idea\(\PageIndex{1}\) central de ANOVA: comparar dentro y entre varianzas.

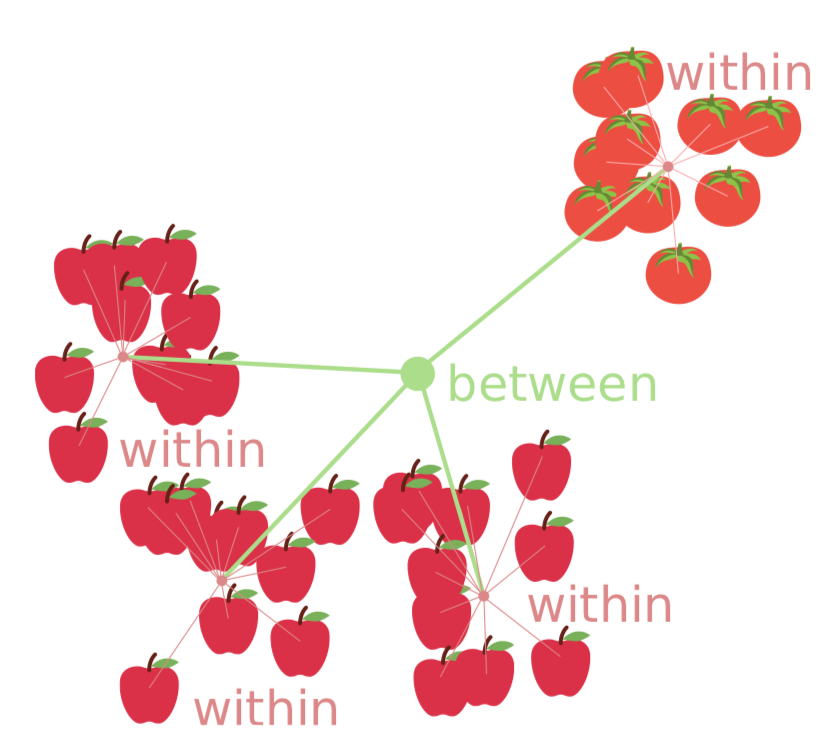
La segunda suposición es la homogineidad de varianza (homocedasticidad), o, más simple, similitud de varianzas. Esto es más importante y significa que se recolectaron submuestras con métodos similares.

El tercer supuesto es más general. Ya se describió en el primer capítulo: independencia de muestras. Sin embargo, el “ANOVA de mediciones repetidas” es posible, pero requiere un enfoque más específico.

Todos los supuestos deben ser verificados antes del análisis.

La mejor forma de organización de datos para el ANOVA es la forma larga explicada anteriormente: dos variables, una de ellas contiene datos numéricos, mientras que la otra describe la agrupación (en terminología R, es un factor). A continuación, creamos los datos artificiales que describen tres tipos de color de cabello, altura (en cm) y peso (en kg) de 90 personas:

Código\(\PageIndex{1}\) (R):

hwc <- read.table("data/hwc.txt", h=TRUE)
str(hwc)
boxplot(WEIGHT ~ COLOR, data=hwc, ylab="Weight, kg")

(Tenga en cuenta que las muescas y otras “campanas y silbatos” no ayudan aquí porque queremos estimar las diferencias conjuntas; la trama de caja cruda es probablemente la mejor opción).

Código\(\PageIndex{2}\) (R):

hwc <- read.table("data/hwc.txt", h=TRUE)
Normality <- function(a) {ifelse(shapiro.test(a)$p.value < 0.05, "NOT NORMAL", "NORMAL")}
sapply(hwc[sapply(hwc, is.numeric)], Normality) # asmisc.r
tapply(hwc$WEIGHT, hwc$COLOR, var)

(Obsérvese el uso de double sapply () para verificar la normalidad solo para columnas de medición.)

Parece que se cumplen ambos supuestos: la varianza es al menos similar y las variables son normales. Ahora ejecutamos el núcleo ANOVA:

Código\(\PageIndex{3}\) (R):

hwc <- read.table("data/hwc.txt", h=TRUE)
wc.aov <- aov(WEIGHT ~ COLOR, data=hwc)
summary(wc.aov)

Esta salida es un poco más complicada que la salida de pruebas de dos muestras, pero contiene elementos similares (de más a menos importantes):

1. valor p (expresado como Pr (>F)) y su significado;

2. estadística (valor F);

3. grados de libertad (Df)

Todos los números anteriores deben ir al reporte. Además, también hay:

1. varianza dentro de las columnas (Sum Sq para Residuales);

2. varianza entre columnas (Sum Sq para COLOR);

3. varianzas medias (Sum Sq dividido por Df)

(La gran varianza es solo una suma de varianzas entre y dentro de columnas).

Si ya se conocen grados de libertad, es bastante fácil calcular el valor F y el valor p manualmente, paso a paso:

Código\(\PageIndex{4}\) (R):

hwc <- read.table("data/hwc.txt", h=TRUE)
df1 <- 2
df2 <- 87
group.size <- 30
(sq.between <- sum(tapply(hwc$WEIGHT, hwc$COLOR, function(.x) (mean(.x) - mean(hwc$WEIGHT))^2))*group.size)
(mean.sq.between <- sq.between/df1)
(sq.within <- sum(tapply(hwc$WEIGHT, hwc$COLOR, function(.x) sum((.x - mean(.x))^2))))
(mean.sq.within <- sq.within/df2)
(f.value <- mean.sq.between/mean.sq.within)
(p.value <- (1 - pf(f.value, df1, df2)))

Por supuesto, R calcula todo eso automáticamente, además también toma en cuenta todas las posibles variantes de cálculos, requeridas para datos con otra estructura. Relacionado con el ejemplo anterior también está que para reportar ANOVA, la mayoría de las investigaciones listan tres cosas: dos valores para grados de libertad, valor F y, por supuesto, valor p.

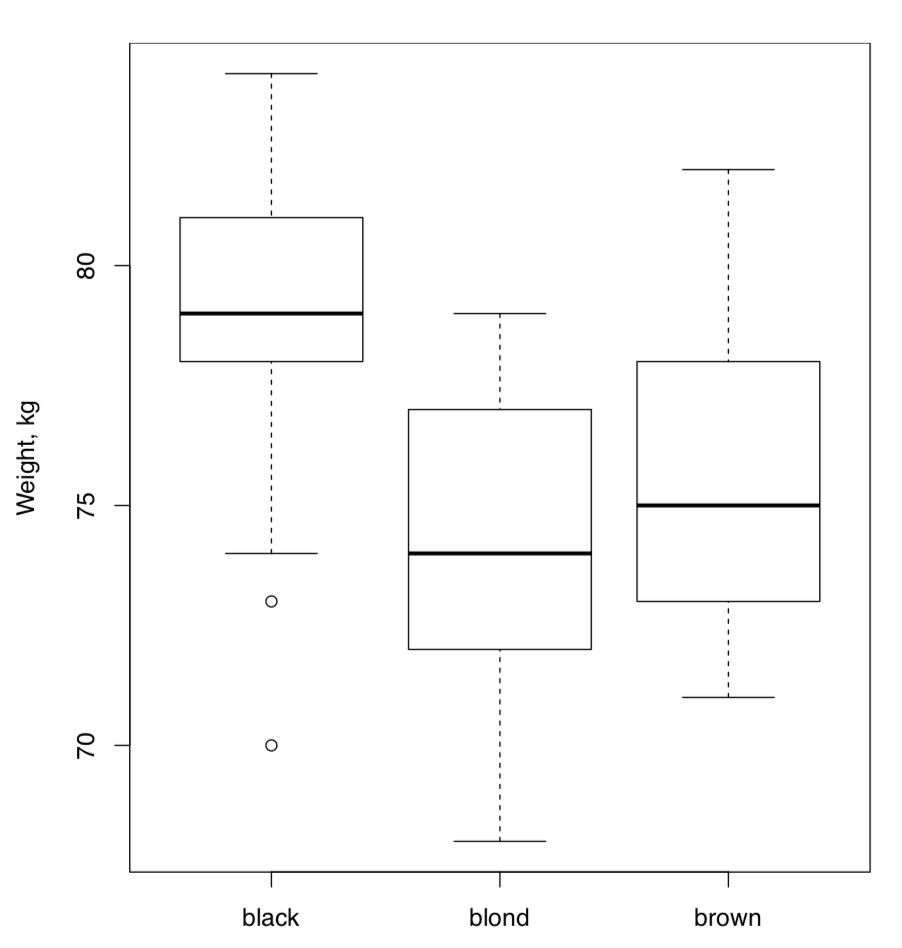
Con todo, este valor p de ANOVA es tan pequeño que H\(_0\) debe ser rechazado a favor de la hipótesis de que al menos una muestra es diferente. Recuerde, ANOVA no dice qué muestra es, pero las gráficas de caja (Figura\(\PageIndex{2}\)) sugieren que esta podría ser gente con pelos negros.

Para verificar el segundo supuesto de ANOVA, que las varianzas deben ser al menos similares, homogéneas, a veces es suficiente mirar la varianza de cada grupo con tapply () como arriba o con aggregate ():

Código\(\PageIndex{5}\) (R):

hwc <- read.table("data/hwc.txt", h=TRUE)
aggregate(hwc[,-1], by=list(COLOR=hwc[, 1]), var)

Figura\(\PageIndex{2}\) ¿Hay diferencia de peso entre personas con diferente color de pelo? (Datos artificiales.)

Pero mejor es probar si las varianzas son iguales con, por ejemplo, bartlett.test () que tiene la misma interfaz de fórmula:

Código\(\PageIndex{6}\) (R):

hwc <- read.table("data/hwc.txt", h=TRUE)
bartlett.test(WEIGHT ~ COLOR, data=hwc)

(La hipótesis nula de la prueba de Bartlett es la igualdad de varianzas).

La alternativa es la prueba no paramétrica de Fligner-Killeen:

Código\(\PageIndex{7}\) (R):

hwc <- read.table("data/hwc.txt", h=TRUE)
fligner.test(WEIGHT ~ COLOR, data=hwc)

(Nulo es lo mismo que en la prueba de Bartlett.)

El primer supuesto de ANOVA también podría verificarse aquí directamente:

Código\(\PageIndex{8}\) (R):

hwc <- read.table("data/hwc.txt", h=TRUE)
wc.aov <- aov(WEIGHT ~ COLOR, data=hwc)
Normality <- function(a) {ifelse(shapiro.test(a)$p.value < 0.05, "NOT NORMAL", "NORMAL")}
Normality(wc.aov$residuals)

El tamaño del efecto del ANOVA se llama\(\eta^2\) (eta al cuadrado). Hay muchas formas de calcular eta al cuadrado pero la más simple se deriva del modelo lineal (ver en las siguientes secciones). Es útil definir\(\eta^2\) como una función:

Código\(\PageIndex{9}\) (R):

Eta2 <- function(aov){summary.lm(aov)$r.squared}

y luego usarlo para los resultados tanto del ANOVA clásico como de la prueba unidireccional (ver abajo):

Código\(\PageIndex{10}\) (R):

Eta2 <- function(aov){summary.lm(aov)$r.squared}
hwc <- read.table("data/hwc.txt", h=TRUE)
wc.aov <- aov(WEIGHT ~ COLOR, data=hwc)
(ewc <- Eta2(wc.aov))
Mag(ewc) # asmisc.r

La segunda función es un intérprete para medidas\(\eta^2\) de tamaño de efecto similares (como coeficiente de\(r\) correlación o R\(^2\) de modelo lineal).

Si es necesario calcular los tamaños de efecto para cada par de grupos, son aplicables las mediciones del tamaño del efecto de dos muestras como el coeficiente de divergencia (K de Lyobishchev).

Un ejemplo más del ANOVA unidireccional clásico proviene de los datos incrustados en R (haz boxplot tú mismo):

Código\(\PageIndex{11}\) (R):

Normality <- function(a) {ifelse(shapiro.test(a)$p.value < 0.05, "NOT NORMAL", "NORMAL")}
Normality(chickwts$weight)
bartlett.test(weight ~ feed, data=chickwts)
boxplot(weight ~ feed, data=chickwts)
chicks.aov <- aov(weight ~ feed, data=chickwts)
summary(chicks.aov)
Eta2(chicks.aov)
Eta2 <- function(aov){summary.lm(aov)$r.squared}
Mag(Eta2(chicks.aov)) # asmisc.r

En consecuencia, existe una diferencia muy alta entre los pesos de los pollos en diferentes dietas.

Si existe el objetivo de encontrar estadísticamente la (s) muestra (s) divergente (s), se puede usar la prueba t por pares post hoc que tiene en cuenta el problema de las comparaciones múltiples descritas anteriormente; esta es solo una forma compacta de ejecutar muchas pruebas t y ajustar los valores p resultantes:

Código\(\PageIndex{12}\) (R):

hwc <- read.table("data/hwc.txt", h=TRUE)
pairwise.t.test(hwc$WEIGHT, hwc$COLOR)

(Esta prueba utiliza por defecto el método Holm de corrección del valor p. Otra forma es la corrección de Bonferroni que se explica a continuación. Todas las formas disponibles de corrección son accesibles a través de la función p.ajustar ().)

Similar al resultado de la prueba t por pares (pero más detallado) es el resultado de la prueba de diferencias significativas honestas de Tukey (Tukey HSD):

Código\(\PageIndex{13}\) (R):

hwc <- read.table("data/hwc.txt", h=TRUE)
wc.aov <- aov(WEIGHT ~ COLOR, data=hwc)
TukeyHSD(wc.aov)

¿Nuestros grupos son diferentes también por alturas? En caso afirmativo, ¿los cabellos negros siguen siendo diferentes?

Las pruebas post hoc generan valores p para que no midan nada. Si es necesario calcular los tamaños de los efectos de grupo a grupo, generalmente son aplicables dos medidas de efecto de muestras (como la K de Lyobishchev). Para entender los efectos por pares, es posible que desee usar la función personalizada PairWise.eff () que se basa en double sapply ():

Código\(\PageIndex{14}\) (R):

hwc <- read.table("data/hwc.txt", h=TRUE)
pairwise.Eff(hwc$WEIGHT, hwc$COLOR, eff="cohen.d") # asmisc.r

El siguiente ejemplo es de nuevo a partir de los datos incrustados (haz boxplot tú mismo):

Código\(\PageIndex{15}\) (R):

Normality <- function(a) {ifelse(shapiro.test(a)$p.value < 0.05, "NOT NORMAL", "NORMAL")}
Normality(PlantGrowth$weight)
bartlett.test(weight ~ group, data=PlantGrowth)
plants.aov <- aov(weight ~ group, data=PlantGrowth)
summary(plants.aov)
Eta2 <- function(aov){summary.lm(aov)$r.squared}
Eta2(plants.aov)
Mag(Eta2(plants.aov)) # asmisc.r
boxplot(weight ~ group, data=PlantGrowth)
with(PlantGrowth, pairwise.t.test(weight, group))

Como resultado, los rendimientos de las plantas a partir de dos condiciones de tratamiento son diferentes, pero no hay diferencia entre cada una de ellas y el testigo. Sin embargo, el tamaño del efecto general si este experimento es alto.

Si las varianzas no son similares, entonces oneway.test () reemplazará al ANOVA simple (unidireccional):

Código\(\PageIndex{16}\) (R):

hwc2 <- read.table("data/hwc2.txt", h=TRUE)
boxplot(WEIGHT ~ COLOR, data=hwc2)
Normality <- function(a) {ifelse(shapiro.test(a)$p.value < 0.05, "NOT NORMAL", "NORMAL")}
sapply(hwc2[, 2:3], Normality) # asmisc.r
tapply(hwc2$WEIGHT, hwc2$COLOR, var)
bartlett.test(WEIGHT ~ COLOR, data=hwc2)
oneway.test(WEIGHT ~ COLOR, data=hwc2)
Eta2 <- function(aov){summary.lm(aov)$r.squared}
(e2 <- Eta2(aov(WEIGHT ~ COLOR, data=hwc2)))
Mag(e2)
pairwise.t.test(hwc2$WEIGHT, hwc2$COLOR) # most applicable post hoc

(Aquí se utilizó otro archivo de datos donde las variables son normales pero las varianzas de grupo no son homogéneas. Por favor, haga boxplot y verifique los resultados de la prueba post hoc usted mismo.)

¿Y si los datos no son normales?

La primera solución es aplicar alguna transformación que podría convertir los datos en normales:

Código\(\PageIndex{17}\) (R):

Normality <- function(a) {ifelse(shapiro.test(a)$p.value < 0.05, "NOT NORMAL", "NORMAL")}
Normality(InsectSprays$count) # asmisc.r
Normality(sqrt(InsectSprays$count))

Sin embargo, la misma transformación podría influir en la varianza:

Código\(\PageIndex{18}\) (R):

bartlett.test(sqrt(count) ~ spray, data=InsectSprays)$p.value

Frecuentemente, es mejor usar el reemplazo ANOVA no paramétrico, prueba de Kruskall-Wallis:

Código\(\PageIndex{19}\) (R):

hwc3 <- read.table("data/hwc3.txt", h=TRUE)
boxplot(WEIGHT ~ COLOR, data=hwc3)
sapply(hwc3[, 2:3], Normality) # asmisc.r
kruskal.test(WEIGHT ~ COLOR, data=hwc3)

(Nuevamente, se utilizó otra variante del archivo de datos, aquí las variables ni siquiera son normales. Por favor, haga boxplot usted mismo.)

El tamaño del efecto de la prueba de Kruskall-Wallis podría calcularse con\(\epsilon^2\):

Código\(\PageIndex{20}\) (R):

hwc3 <- read.table("data/hwc3.txt", h=TRUE)
Epsilon2 <- function(kw, n) # n is the number of cases{unname(kw$statistic/((n^2 - 1)/(n+1)))}
kw <- kruskal.test(WEIGHT ~ COLOR, data=hwc3)
Epsilon2(kw, nrow(hwc3))
Mag(Epsilon2(kw, nrow(hwc3))) # asmisc.r

El tamaño total del efefct es alto, también es visible bien en la parcela de caja (hágalo usted mismo):

Código\(\PageIndex{21}\) (R):

hwc3 <- read.table("data/hwc3.txt", h=TRUE)
boxplot(WEIGHT ~ COLOR, data=hwc3)

Para saber qué muestra está desviada, use la prueba post hoc no paramétrica:

Código\(\PageIndex{22}\) (R):

hwc3 <- read.table("data/hwc3.txt", h=TRUE)
pairwise.wilcox.test(hwc3$WEIGHT, hwc3$COLOR)

(Hay múltiples advertencias sobre los lazos. Para deshacerse de ellos, reemplace el primer argumento con jitter (hwc3$height). Sin embargo, dado que jitter () agrega ruido aleatorio, es mejor tener cuidado y repetir el análisis varias veces si los valores p están cerca del umbral como aquí).

Otra prueba post hoc para el diseño unidireccional no paramétrico es la prueba de Dunn. Hay un paquete dunn.test separado:

Código\(\PageIndex{23}\) (R):

hwc3 <- read.table("data/hwc3.txt", h=TRUE)
library(dunn.test)
dunn.test(hwc3$WEIGHT, hwc3$COLOR, method="holm", altp=TRUE)

(La salida es más avanzada pero los resultados generales son similares. Existen más pruebas post hoc como la prueba de Dunnett en el paquete multcomp.)

No es necesario verificar la homogeneidad de varianza antes de la prueba de Kruskall-Wallis, pero tenga en cuenta que asume que las formas de distribución no son radicalmente diferentes entre muestras. Si no es así, una de las soluciones alternativas es transformar primero los datos, ya sea logarítmicamente o con raíz cuadrada, o a las filas\(^{[2]}\), o incluso de la manera más sofisticada. Otra opción es aplicar pruebas de permutación (ver Apéndice). Como prueba post hoc, es posible usar PairWise.rro.test () de asmisc.r que no asume similitud de distribuciones.

La siguiente figura (Figura\(\PageIndex{3}\)) contiene el diagrama de Euler que resume lo dicho anteriormente sobre diferentes supuestos y formas de análisis simples similares a Anova. Tenga en cuenta que hay muchos más procedimientos de pruebas post hoc que se enumeran, y muchos de ellos se implementan en varios paquetes R.

La secuencia típica de procedimientos relacionados con el análisis unidireccional se enumera a continuación:

• Comprobar si la estructura de datos es adecuada (head (), str (), summary ()), es larga o corta

• Parcela (por ejemplo, boxplot (), beanplot ())

• Normalidad, con función de trama o normalidad ()

• Homogeneidad de varianza (homocedasticidad) (con bartlett.test () o fligner.test ())

• Procedimiento básico (aov clásico (), oneway.test () o kruskal.test ())

• Opcionalmente, tamaño del efecto (\(\eta^2\)o\(\epsilon^2\) con la fórmula apropiada)

• Prueba post hoc, por ejemplo TukeyHSD (), pairwise.t.test (), dunn.test () o parwise.wilcox.test ()

Figura\(\PageIndex{3}\) Aplicabilidad de diferentes procedimientos similares a Anova y pruebas post hoc relacionadas. Por favor, léelo de abajo hacia arriba.

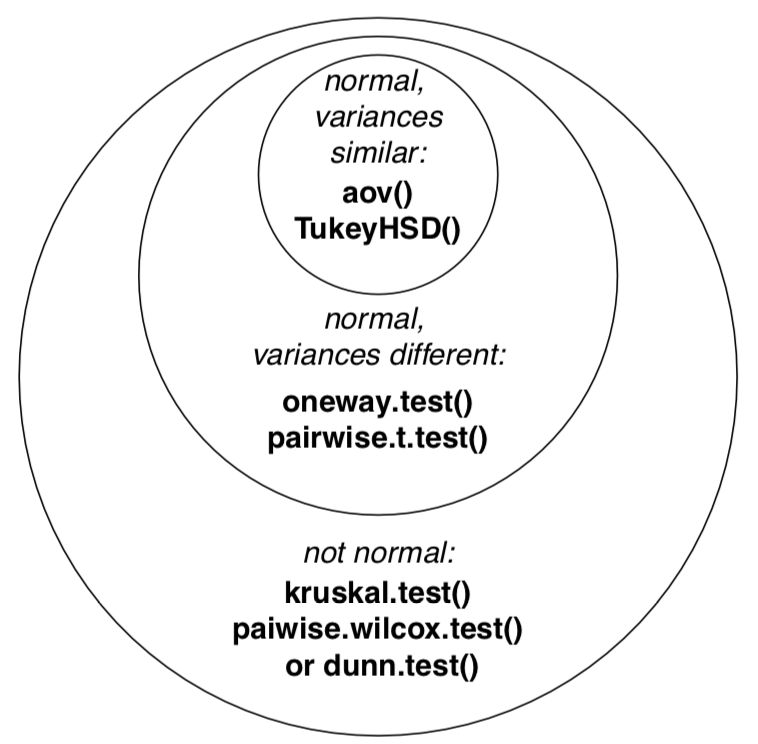
En el repositorio abierto, el archivo de datos melampyrum.txt contiene resultados de mediciones de trigo vacuno (Melampyrum spp.) en múltiples localidades. Por favor, encuentre si hay una diferencia en altura de planta y longitud de hoja entre plantas de diferentes localidades. ¿Qué localidades son divergentes en cada caso? Para entender la estructura de los datos, utilice el archivo complementario melampyrum_c.txt.

En definitiva, si se tienen dos o más muestras representadas con datos de medición, la siguiente tabla ayudará a investigar las diferencias:

Más entonces de una manera

El ANOVA simple y unidireccional utiliza solo un factor en la fórmula. Sin embargo, con frecuencia necesitamos analizar los resultados de experimentos u observaciones más sofisticados, cuando los datos se dividen dos o más veces y posiblemente por principios diferentes.

Nuestro libro no pretende profundizar, y lo siguiente es solo una introducción al mundo del diseño y análisis de experimentos. Algunos términos, sin embargo, son importantes para explicar:

	dos muestras	más de dos muestras
Paso 1. Gráfico	diagrama de caja (); parcela de frijol ()
Paso 2. Normalidad etc.	Normalidad (); hist (); qqnorm () y qqine (); opcionalmente: bartlett. test () o flingner.test ()
Paso 3. Test	t.test (); wilcoxon.test ()	aov (); oneway.test (); kruskal.test ()
Paso 4. Efecto	cohen.d (); cliff.delta ()	opcionalmente: Eta2 (); Epsilon2 ()
Paso 5. Pares	NA	TukeyHSD (); par.t.test (); dunn.test ()

Tabla\(\PageIndex{1}\) Cómo investigar las diferencias entre muestras numéricas en R.

Bidireccionales

Esto es cuando los datos contienen dos factores independientes. Ver, por ejemplo,? Datos de crecimiento de dientes incrustados en R. Con más factores, son posibles los diseños de tres y más formas.

Mediciones repetidas

Esto es análogo a los casos pareados de dos muestras, pero con tres y más mediciones en cada sujeto. Este tipo de diseño puede requerir enfoques específicos. ¿Ves? Naranja o? Datos loblolly.

Desbalanceado

Cuando los grupos tienen diferentes tamaños y/o algunas combinaciones de factores están ausentes, entonces el diseño está desequilibrado; esto a veces complica los cálculos.

Interacción

Si hay más de un factor, podrían trabajar juntos (interactuar) para producir respuesta. En consecuencia, con dos factores, el análisis debe incluir estadísticas para cada uno de ellos más estadística separada para la interacción, tres valores en total. Volveremos a la interacción más adelante, en sección sobre ANCOVA (“Muchas líneas”). Aquí solo mencionamos la manera útil de mostrar las interacciones visualmente, con la gráfica de interacción (Figura\(\PageIndex{4}\)):

Código\(\PageIndex{24}\) (R):

with(ToothGrowth, interaction.plot(supp, dose, len))

(Es, por ejemplo, fácil de ver en esta trama de interacción que con la dosis 2, el tipo de suplemento no importa.)

Efectos aleatorios y fijos

Algunos factores son irrelevantes para la investigación pero participan en la respuesta, por lo que deben ser incluidos en el análisis. Otros factores son planeados e intencionales.

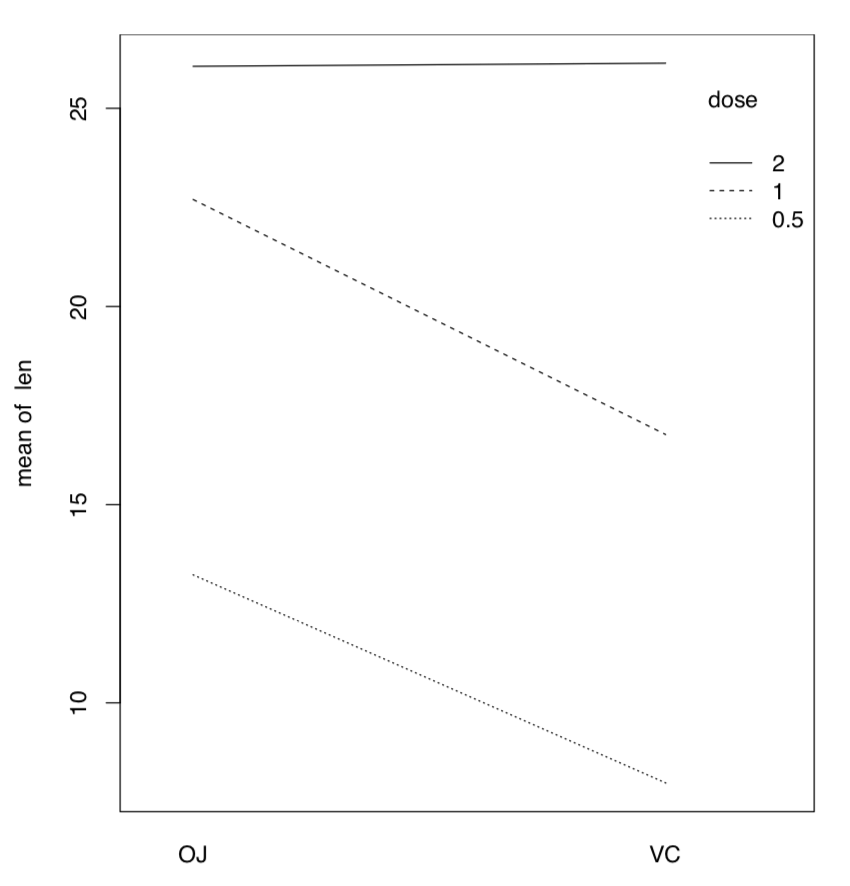
Figura Gráfica de\(\PageIndex{4}\) interacción para datos de crecimiento de dientes.

Respectivamente, se les llama efectos aleatorios y fijos. Esta diferencia también influye en los cálculos.

Referencias

1. Bennett C.M., Wolford G.L., Miller M.B. 2009. El control de principios de los falsos positivos en neuroimag- ing. Neurociencia social cognitiva y afectiva 4 (4): 417—422, https://www.ncbi.nlm.nih.gov/ PMC/artículos/PMC2799957/

2. Al igual que se implementa en el paquete ARTool; también es posible utilizar diseños no paramétricos de múltiples vías.