5.1: ¿Qué es una prueba estadística?

Supongamos que comparamos dos conjuntos de números, medidas que vinieron de dos muestras. Por comparación, encontramos que son diferentes. Pero ¿cómo saber si esta diferencia no surgió por casualidad? Es decir, ¿cómo decidir que nuestras dos muestras son realmente diferentes, es decir, no vinieron de una población?

Estas muestras podrían ser, por ejemplo, mediciones de la presión arterial sistólica. Si estudiamos el medicamento que potencialmente baja la presión arterial, es sensato mezclarlo aleatoriamente con un placebo, y luego pedir a los miembros del grupo que reporten su presión arterial el primer día del ensayo y, diciendo, el décimo día. Entonces la diferencia entre dos mediciones permitirá decidir si hay algún efecto:

Código\(\PageIndex{1}\) (R):

bpress <- read.table("data/bpress.txt", h=TRUE)
head(bpress)
drug.d <- bpress$DRUG.10 - bpress$DRUG.1
placebo.d <- bpress$PLACEBO.10 - bpress$PLACEBO.1
mean(drug.d - placebo.d)
boxplot(bpress)

Ahora, hay un efecto prometedor, diferencia suficiente entre las diferencias de presión arterial con fármaco y con placebo. Esto también es bien visible con parcelas de caja (compruébalo tú mismo). ¿Cómo probarlo? Ya sabemos usar el valor p, pero es el final de la cadena lógica. Empecemos desde el principio.

Hipótesis estadísticas

Los filósofos postularon que la ciencia nunca puede probar una teoría, sino sólo desmentirla. Si recolectamos 1000 hechos que sustentan una teoría, no significa que la hayamos probado, es posible que la prueba número 100 la desacredite. Es por ello que en las pruebas estadísticas comúnmente utilizamos dos hipótesis. El que estamos tratando de probar se llama hipótesis alternativa (\(H_1\)). La otra, por defecto, se llama hipótesis nula (\(H_0\)). La hipótesis nula es una proposición de ausencia de algo (por ejemplo, diferencia entre dos muestras o relación entre dos variables). No podemos probar la hipótesis alternativa, pero podemos rechazar la hipótesis nula y, por lo tanto, cambiar a la alternativa. Si no podemos rechazar la hipótesis nula, entonces debemos quedarnos con ella.

Errores estadísticos

Con dos hipótesis, hay cuatro posibles resultados (Tabla\(\PageIndex{1}\)).

Los resultados primero (a) y último (d) son casos ideales: o aceptamos la hipótesis nula que es correcta para la población estudiada, o rechazamos\(H_0\) cuando está equivocada.

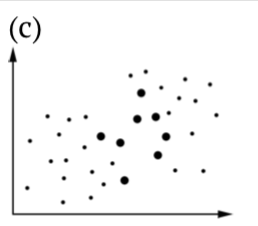
Si hemos aceptado la hipótesis alternativa, cuando no es cierta, hemos cometido un error estadístico Tipo I —hemos encontrado un patrón que no existe. Esta situación suele llamarse “falso positivo”, o “falsa alarma”. La probabilidad de cometer un error Tipo I está relacionada con un valor p que siempre se reporta como uno de los resultados de una prueba estadística. De hecho, el valor p es una probabilidad de tener el mismo o mayor efecto si la hipótesis nula es verdadera.

Imagínese oficial de seguridad en el turno nocturno que escucha algo extraño. Hay dos opciones: saltar y verificar si este ruido es un indicio de algo importante, o continuar relajándose. Si el ruido exterior no es importante o incluso no real pero el oficial saltó, este es el error Tipo I. La probabilidad de escuchar el ruido sospechoso cuando en realidad no pasa nada en un valor p.

muestra\ población	Nulo es verdadero	La alternativa es verdadera
Aceptar nulo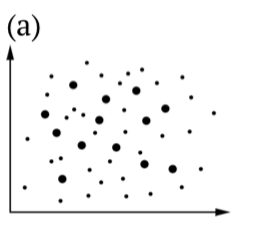
Aceptar alternativa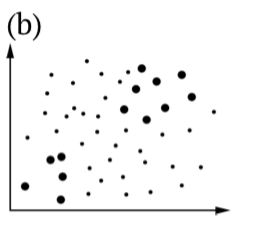

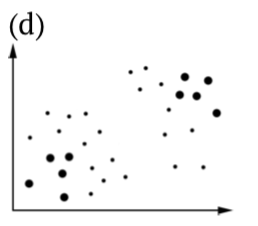Cuadro Hipótesis\(\PageIndex{1}\) estadísticas, incluyendo ilustraciones de (b) Errores Tipo I y (c) Tipo II. Los puntos más grandes son muestras, todos los puntos son población (es).

Para el oficial de seguridad, probablemente sea mejor cometer error Tipo I que saltarse algo importante. No obstante, en la ciencia la situación es opuesta: siempre nos quedamos con el\(H_0\) cuando la probabilidad de cometer un error Tipo I es demasiado alta. Filosóficamente, esta es una variante de la navaja de Occam: los científicos siempre prefieren no introducir nada (es decir, cambiar a alternativa) sin necesidad.

el hombre que por sí solo salvó al mundo de la guerra nuclear

Este enfoque se pudo encontrar también en otras esferas de nuestra vida. Lee el artículo de Wikipedia sobre Stanislav Petrov (https://en.Wikipedia.org/wiki/Stanislav_Petrov); este es otro ejemplo cuando la falsa alarma es demasiado costosa.

La pregunta obvia es ¿qué probabilidad es “demasiado alta”? La respuesta convencional coloca ese umbral en 0.05; la hipótesis alternativa se acepta si el valor p es menor al 5% (nivel de confianza superior al 95%). En medicina, con la vida humana como juego, los umbrales se fijan aún más estrictamente, en 1% o incluso 0.1%. Por el contrario, en las ciencias sociales, es frecuente aceptar el 10% como umbral. Lo que se escogió como umbral, se debe fijar a priori, antes de cualquier prueba. No se permite modificar umbral para encontrar una excusa para la decisión estadística en mente.

Figura\(\PageIndex{1}\) Esquema de decisión estadística (para prueba de 1 cola). \(\alpha\)es la probabilidad de error Tipo I,\(\beta\) —de error Tipo II. Antes de la prueba, debemos establecer\(\alpha\), generalmente en 0.05. Luego usamos datos originales para calcular la estadística (adivinar la ubicación de la línea vertical negra). A continuación, utilizamos estadística para calcular el valor p. Finalmente, si el valor p es menor entonces\(\alpha\), rechazamos la hipótesis nula.

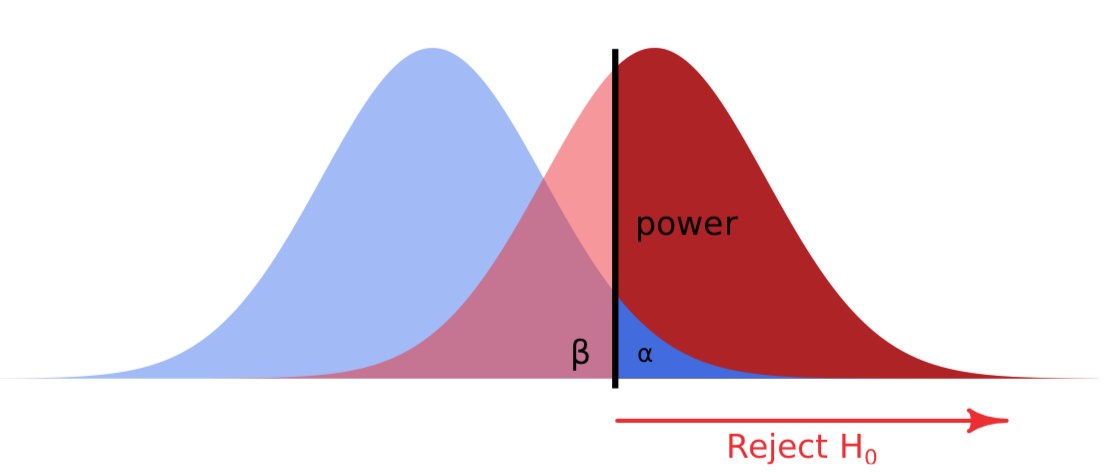
Aceptar la hipótesis nula cuando de hecho la alternativa es verdadera es un error estadístico Tipo II —falla al detectar un patrón que realmente existe. Esto se llama “falso negativo”, “descuido”. Si el descuidado oficial de seguridad no saltó cuando el ruido exterior es realmente importante, este es el error Tipo II. La probabilidad de cometer error tipo II se expresa como potencia de la prueba estadística (Figura\(\PageIndex{1}\)). Cuanto menor es esta probabilidad, más poderosa es la prueba.