Saltar al contenido principal
LibreTexts Español

6.4: Respuestas a los ejercicios

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    150158

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Correlación y modelos lineales

    Respuesta a la pregunta de los rasgos humanos. Inspeccionar los datos, cargarlos y verificar el objeto:

    Código\(\PageIndex{1}\) (R):

    traits <- read.table("data/traits.txt", h=TRUE, row.names=1)
str(traits)

    Los datos son binarios, por lo que la correlación de Kendall es más natural:

    Código\(\PageIndex{2}\) (R):

    traits <- read.table("data/traits.txt", h=TRUE, row.names=1)
Cor(traits, method="kendall", dec=1) # asmisc.r
traits.c <- cor(traits, method="kendall")
Topm(traits.c) # asmisc.r

    Visualizaremos la correlación con la Pleiad (), una de sus ventajas es mostrar qué correlaciones están conectadas, agrupadas, las llamadas “pléyadas de correlación”:

    Código\(\PageIndex{3}\) (R):

    traits <- read.table("data/traits.txt", h=TRUE, row.names=1)
Cor(traits, method="kendall", dec=1) # asmisc.r
traits.c <- cor(traits, method="kendall")
Pleiad(traits.c, corr=TRUE, lcol=1, legend=FALSE, off=1.12, pch=21, bg="white", cex=1.1) # asmisc.r

    (Mira en la página de título para ver correlaciones. Una pleíada, la barbilla, la lengua y el pulgar es la más aparente.)

    Respuesta a la pregunta de la dependencia lineal entre estatura y peso para los datos artificiales. La correlación está presente pero la dependencia es débil (Figura\(\PageIndex{1}\)):

    Código\(\PageIndex{4}\) (R):

    hwc <- read.table("data/hwc.txt", h=TRUE)
cor.test(hwc$WEIGHT, hwc$HEIGHT)
w.h <- lm(WEIGHT ~ HEIGHT, data=hwc)
summary(w.h)
plot(WEIGHT ~ HEIGHT, data=hwc, xlab="Height, cm", ylab="Weight, kg")
abline(w.h)
Cladd(w.h, data=hwc) # asmisc.r
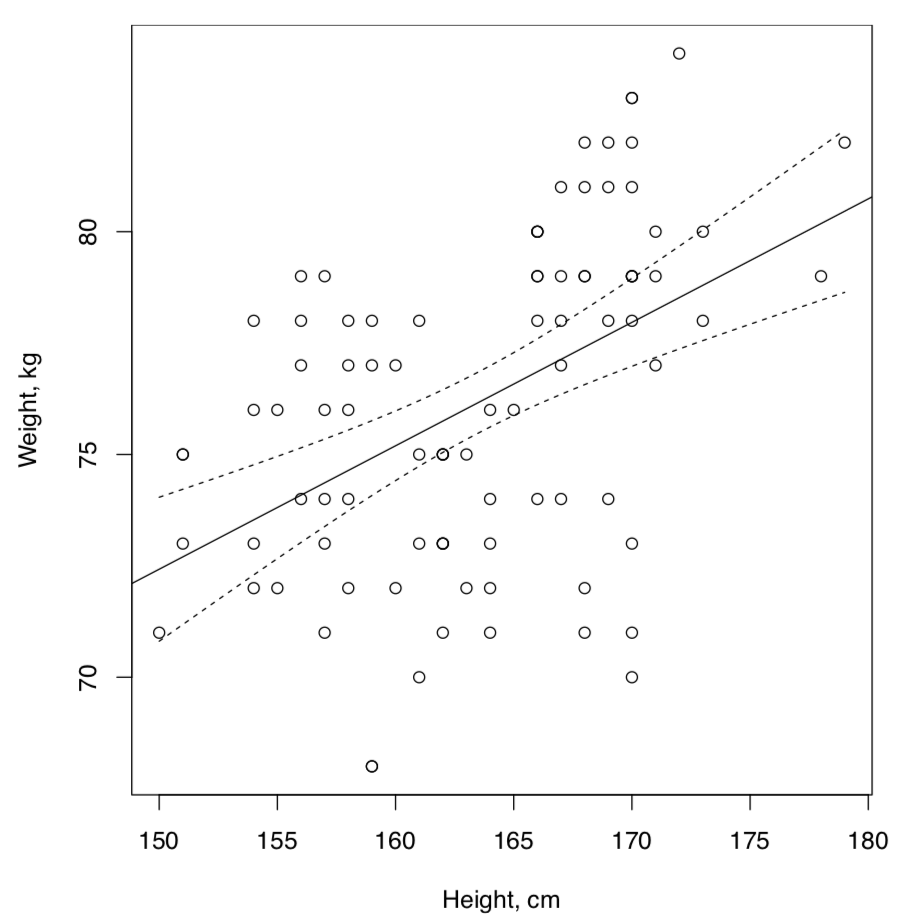
    Screen Shot 2019-01-22 a las 12.52.03 AM.png
    Figura\(\PageIndex{1}\) La dependencia del peso de la altura (datos artificiales)

    La conclusión sobre la dependencia débil se hizo debido a la baja R-cuadrado lo que significa que la variable predictora, la altura, no explica gran parte de la variable dependiente, el peso. Además, muchos residuos se encuentran fuera del IQR. Esto también es fácil de ver en la gráfica donde muchos puntos de datos están distantes de la línea de regresión e incluso de bandas de confianza del 95%.

    Respuesta a la pregunta de draba de primavera. Comprobar archivo, cargar y verificar el objeto:

    Código\(\PageIndex{5}\) (R):

    ee <- read.table("http://ashipunov.info/shipunov/open/erophila.txt", h=TRUE)
str(ee) # asmisc.r

    Ahora, verifique la normalidad y las correlaciones con el método apropiado:

    Código\(\PageIndex{6}\) (R):

    ee <- read.table("http://ashipunov.info/shipunov/open/erophila.txt", h=TRUE)
Normality <- function(a) {ifelse(shapiro.test(a)$p.value < 0.05, "NOT NORMAL", "NORMAL")}
sapply(ee[, 2:4], Normality) # asmisc.r
Topm(cor(ee[, 2:4], method="spearman")) # asmisc.r
with(ee, cor.test(FRUIT.L, FRUIT.MAXW, method="spearman"))

    Por tanto, FRUIT.L y FRUIT.MAXW son los mejores candidatos para el análisis de modelos lineales. Lo trazaremos primero (Figura\(\PageIndex{2}\)):

    Código\(\PageIndex{7}\) (R):

    ee <- read.table("http://ashipunov.info/shipunov/open/erophila.txt", h=TRUE)
ee.lm <- lm(FRUIT.MAXW ~ FRUIT.L, data=ee)
plot(FRUIT.MAXW ~ FRUIT.L, data=ee, type="n")
Points(ee$FRUIT.L, ee$FRUIT.MAXW, scale=.5) # asmisc.r
Cladd(ee.lm, ee, ab.lty=1) # asmisc.r

    (Points () es una variante “única” de pPoints () de lo anterior, y se utilizó porque hay múltiples puntos de datos superpuestos.)

    Finalmente, verifique el modelo lineal y las suposiciones:

    Código\(\PageIndex{8}\) (R):

    ee <- read.table("http://ashipunov.info/shipunov/open/erophila.txt", h=TRUE)
ee.lm <- lm(FRUIT.MAXW ~ FRUIT.L, data=ee)
summary(ee.lm)
plot(ee.lm, which=1)
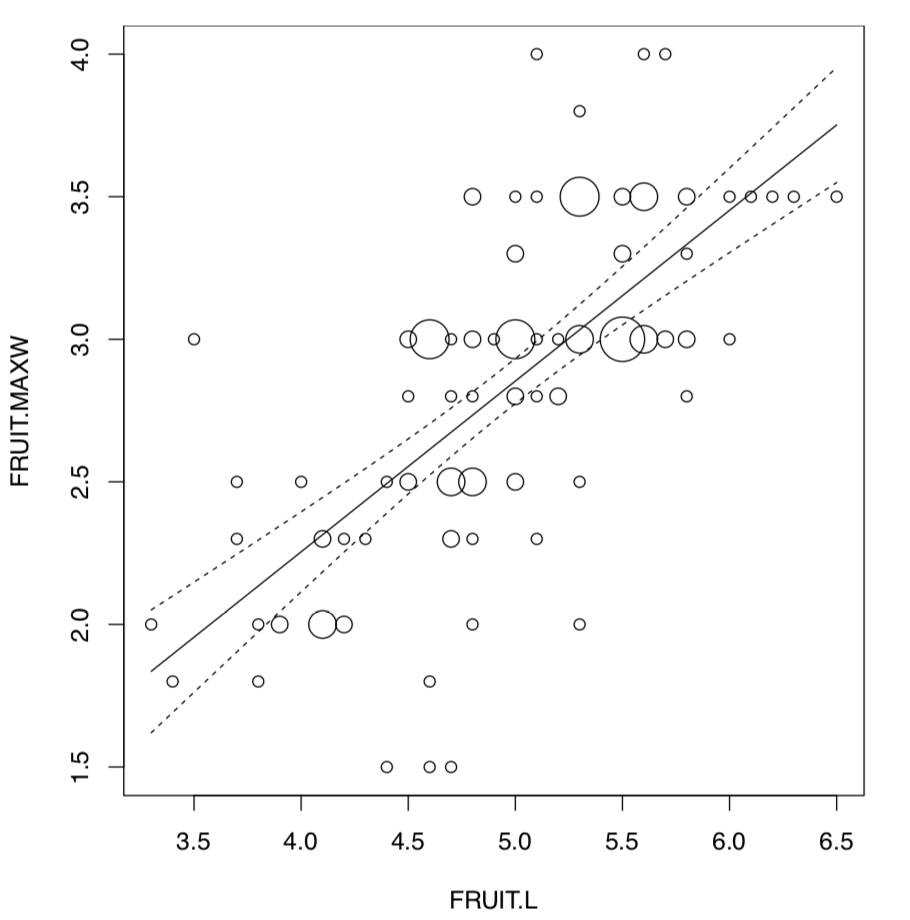
    Screen Shot 2019-01-22 a las 12.55.09 AM.png
    Figura Relación\(\PageIndex{2}\) lineal entre características de frutos de draba primaveral.

    Existe un modelo confiable (valor p: < 2.2e-16) que tiene un alto valor R cuadrado (sqrt (0.4651) = 0.6819824). El coeficiente de pendiente es significativo mientras que la intercepción no lo es. La homogeneidad de los residuos es evidente, su normalidad también está fuera de discusión:

    Código\(\PageIndex{9}\) (R):

    ee <- read.table("http://ashipunov.info/shipunov/open/erophila.txt", h=TRUE)
ee.lm <- lm(FRUIT.MAXW ~ FRUIT.L, data=ee)
Normality <- function(a) {ifelse(shapiro.test(a)$p.value < 0.05, "NOT NORMAL", "NORMAL")}
Normality(ee.lm$residuals)

    Respuesta a la pregunta heterostyly. Primero, inspeccione el archivo, cargue los datos y verifíquelo:

    Código\(\PageIndex{10}\) (R):

    he <- read.table("http://ashipunov.info/shipunov/open/heterostyly.txt", h=TRUE)
str(he)

    Es así como visualizar el fenómeno de heterostyly para todos los datos:

    Código\(\PageIndex{11}\) (R):

    he <- read.table("http://ashipunov.info/shipunov/open/heterostyly.txt", h=TRUE)
boxplot((STYLE.L-STAMEN.L) ~ (STYLE.L-STAMEN.L)>0, names=c("short","long"), data=he)

    (Por favor revise esta parcela usted mismo.)

    Ahora necesitamos visualizar las relaciones lineales de interrogación. Hay muchos puntos de datos superpuestos, así que la mejor manera es emplear la función pPoints () (Figura\(\PageIndex{3}\)):

    Código\(\PageIndex{12}\) (R):

    he <- read.table("http://ashipunov.info/shipunov/open/heterostyly.txt", h=TRUE)
plot(STYLE.L ~ STAMEN.L, data=he, type="n", xlab="Length of stamens, mm", ylab="Length of style, mm")
PPoints(he$SPECIES, he$STAMEN.L, he$STYLE.L, scale=.9, cols=1)
abline(lm(STYLE.L ~ STAMEN.L, data=he[he$SPECIES=="veris", ]))
abline(lm(STYLE.L ~ STAMEN.L, data=he[he$SPECIES=="vulgaris", ]), lty=2)
legend("topright", pch=1:2, lty=1:2, legend=c("Primula veris", "P. vulgaris"), text.font=3)
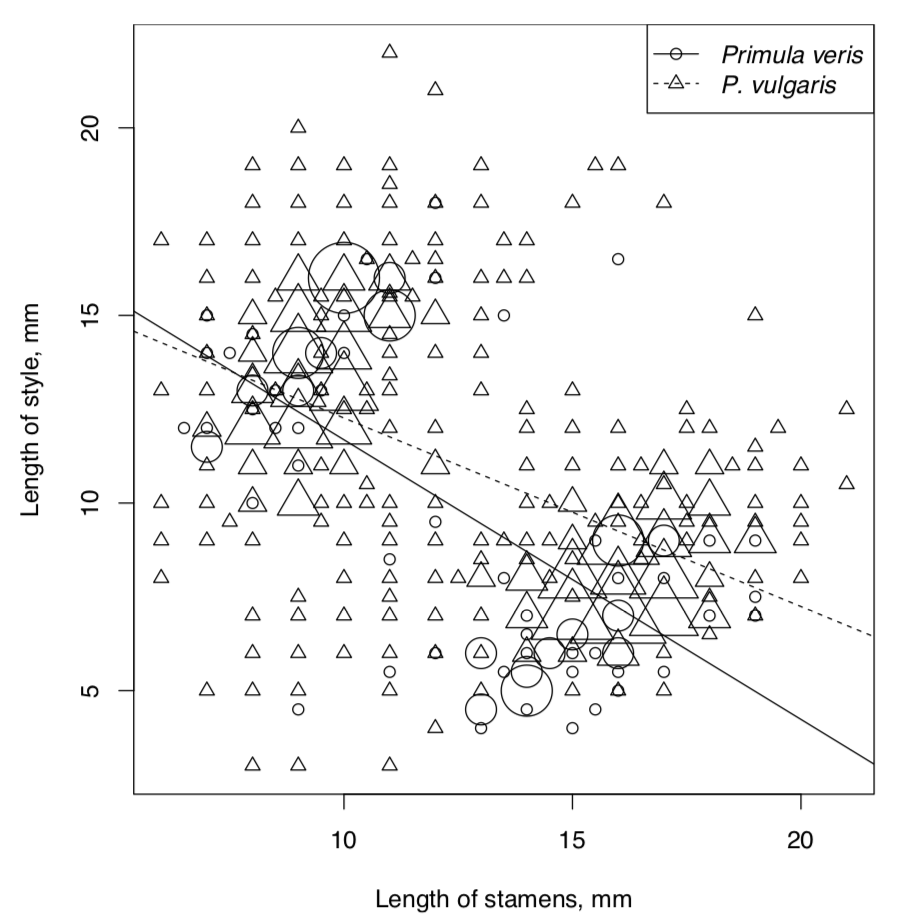
    Screen Shot 2019-01-22 at 1.00.01 AM.png
    Figura Relaciones\(\PageIndex{3}\) lineales dentro de flores de dos especies de onagra. Heterostyly es visible como dos densas “nubes” de puntos de datos.

    Ahora a los modelos. Supondremos que la longitud de los estambres es la variable independiente. Explore, verifique suposiciones y AIC para el modelo completo:

    Código\(\PageIndex{13}\) (R):

    he <- read.table("http://ashipunov.info/shipunov/open/heterostyly.txt", h=TRUE)
summary(he.lm1 <- lm(STYLE.L ~ STAMEN.L * SPECIES, data=he))
plot(he.lm1, which=1:2)
AIC(he.lm1)

    Modelo reducido (aditivo):

    Código\(\PageIndex{14}\) (R):

    he <- read.table("http://ashipunov.info/shipunov/open/heterostyly.txt", h=TRUE)
summary(he.lm2 <- update(he.lm1, . ~ . - STAMEN.L:SPECIES))
AIC(he.lm2)

    El modelo completo es mejor, probablemente debido a interacciones fuertes. Para verificar las interacciones gráficamente es posible también con la gráfica de interacción que tratará la variable independiente como factor:

    Código\(\PageIndex{15}\) (R):

    he <- read.table("http://ashipunov.info/shipunov/open/heterostyly.txt", h=TRUE)
with(he, interaction.plot(cut(STAMEN.L, quantile(STAMEN.L)), SPECIES, STYLE.L))

    Esta parcela técnica (compruébalo tú mismo) muestra las diferencias confiables entre líneas de diferentes especies. Estas diferencias son mayores cuando los estambres son más largos. Esta parcela es más adecuada para el complejo ANOVA pero como ves, funciona también para modelos lineales.

    Respuesta a la pregunta sobre las poblaciones de rocío solar (Drosera). Primero, inspeccione el archivo, luego cárguelo y verifique la estructura del objeto:

    Código\(\PageIndex{16}\) (R):

    dr <- read.table( "http://ashipunov.info/shipunov/open/drosera.txt", h=TRUE)
str(dr) # asmisc.r

    Como se requiere para calcular la correlación, verificar primero la normalidad:

    Código\(\PageIndex{17}\) (R):

    dr <- read.table( "http://ashipunov.info/shipunov/open/drosera.txt", h=TRUE)
Normality <- function(a) {ifelse(shapiro.test(a)$p.value < 0.05, "NOT NORMAL", "NORMAL")}
sapply(dr[,-1], Normality)

    Bueno, a estos datos solo podemos aplicar métodos no paramétricos:

    Código\(\PageIndex{18}\) (R):

    dr <- read.table( "http://ashipunov.info/shipunov/open/drosera.txt", h=TRUE)
dr.cor <- cor(dr[,-1], method="spearman", use="pairwise")
Topm(dr.cor) # asmisc.r
Pleiad(dr.cor, corr=TRUE, legtext=2, legpos="bottom", leghoriz=TRUE, pch=19, cex=1.2) # asmisc.r

    (Tenga en cuenta que se empleó “por pares”, hay muchos NA).

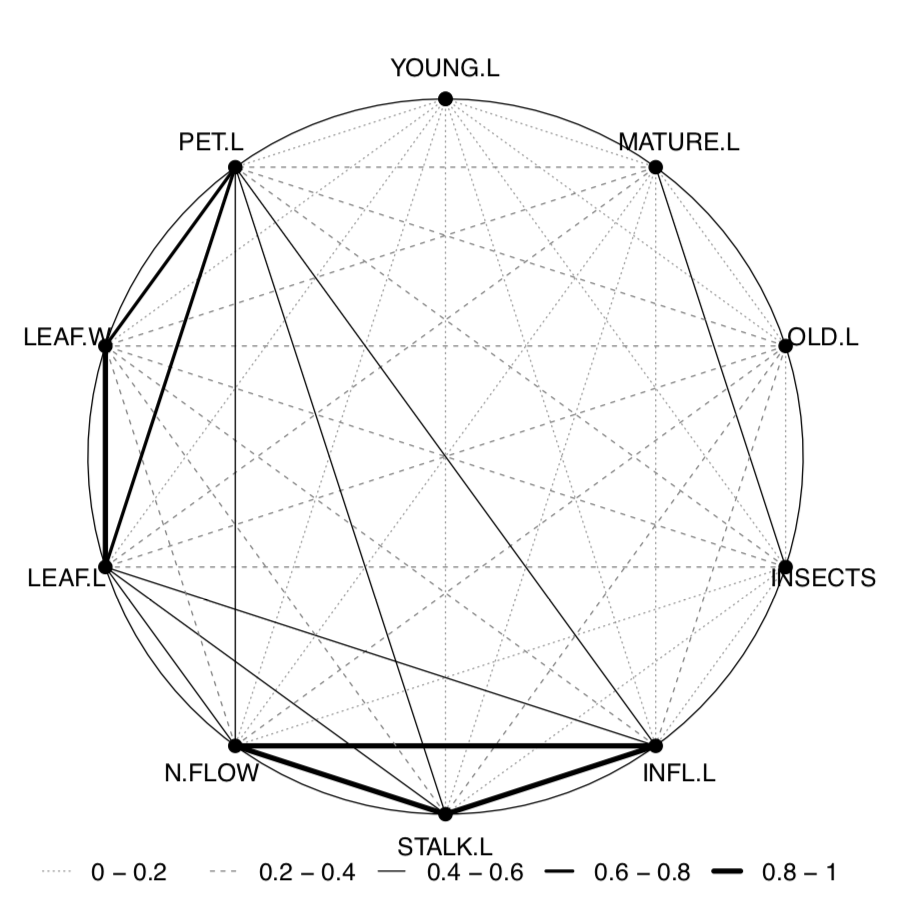
    Screen Shot 2019-01-22 al 1.07.59 AM.png
    Figura\(\PageIndex{4}\) Correlaciones en datos de rocío solar.

    La última parcela (Figura\(\PageIndex{4}\)) muestra dos pleíadas de correlación más importantes: una relacionada con el tamaño de la hoja y otra con inflorescencia.

    Como sabemos ahora qué caracteres están más correlacionados, se procede al modelo lineal. Dado que en el desarrollo del tallo de sol se formó primero, aceptemos STALK.L como variable independiente (influencia), e INFL.L como variable dependiente (respuesta):

    Código\(\PageIndex{19}\) (R):

    dr <- read.table( "http://ashipunov.info/shipunov/open/drosera.txt", h=TRUE)
summary(dr.lm <- lm(INFL.L ~ STALK.L, data=dr))
plot(dr.lm, which=1:2)

    Modelo confiable con alto R-cuadrado. Sin embargo, la normalidad de los residuos no es perfecta (por favor revise las parcelas modelo usted mismo).

    Ahora al análisis de la longitud de la hoja. Determinar cuáles son las tres poblaciones más grandes y subconjuntos de los datos:

    Código\(\PageIndex{20}\) (R):

    dr <- read.table( "http://ashipunov.info/shipunov/open/drosera.txt", h=TRUE)
(largest3 <- rev(sort(table(dr[, 1])))[1:3])
dr3 <- dr[dr$POP %in% names(largest3), ]
dr3$POP <- droplevels(dr3$POP)

    Ahora necesitamos trazarlos y verificar si hay diferencias visuales:

    Código\(\PageIndex{21}\) (R):

    dr <- read.table( "http://ashipunov.info/shipunov/open/drosera.txt", h=TRUE)
largest3 <- rev(sort(table(dr[, 1])))[1:3]
dr3 <- dr[dr$POP %in% names(largest3), ]
boxplot(LEAF.L ~ POP, data=dr3)

    Sí, probablemente existan (por favor revise la parcela usted mismo).

    Vale la pena mirar en similitud de rangos:

    Código\(\PageIndex{22}\) (R):

    dr <- read.table( "http://ashipunov.info/shipunov/open/drosera.txt", h=TRUE)
largest3 <- rev(sort(table(dr[, 1])))[1:3]
dr3 <- dr[dr$POP %in% names(largest3), ]
dr3$POP <- droplevels(dr3$POP)
tapply(dr3$LEAF.L, dr3$POP, mad, na.rm=TRUE)
fligner.test(LEAF.L ~ POP, data=dr3)

    El estadístico de rango robusto, MAD (mediana de desviación absoluta) muestra que las variaciones son similares. También se realizó el análogo no paramétrico de la prueba de Bartlett para ver la significancia estadística de esta similitud. Sí, las varianzas son estadísticamente similares.

    Como tenemos tres poblaciones para analizar, necesitaremos algo parecido a Anova, pero no paramétrico:

    Código\(\PageIndex{23}\) (R):

    dr <- read.table( "http://ashipunov.info/shipunov/open/drosera.txt", h=TRUE)
largest3 <- rev(sort(table(dr[, 1])))[1:3]
dr3 <- dr[dr$POP %in% names(largest3), ]
kruskal.test(LEAF.L ~ POP, data=dr3)

    Sí, hay al menos una población donde la longitud de la hoja es diferente de todas las demás. Para ver cual, necesitamos una prueba post hoc, por pares:

    Código\(\PageIndex{24}\) (R):

    dr <- read.table( "http://ashipunov.info/shipunov/open/drosera.txt", h=TRUE)
largest3 <- rev(sort(table(dr[, 1])))[1:3]
dr3 <- dr[dr$POP %in% names(largest3), ]
dr3$POP <- droplevels(dr3$POP)
pairwise.wilcox.test(dr3$LEAF.L, dr3$POP)

    La población N1 es la más divergente mientras que Q1 no es realmente diferente de L.

    Regresión logística

    Respuesta a la pregunta sobre demostración de objetos. Vamos a ir de la misma manera que en el ejemplo sobre programadores. Después de cargar los datos, los adjuntamos por simplicidad:

    Código\(\PageIndex{25}\) (R):

    seeing <- read.table("data/seeing.txt")
attach(seeing)

    Compruebe el modelo:

    Código\(\PageIndex{26}\) (R):

    seeing <- read.table("data/seeing.txt")
seeing.logit <- glm(V3 ~ V2, family=binomial, data=seeing)
summary(seeing.logit)

    (Al llamar a las variables, tomamos en cuenta el hecho de que R asigna nombres como V1, V2, V3 etc. a columnas “anónimas”.)

    Como se puede ver, el modelo es significativo. Significa que algo de aprendizaje se lleva a cabo dentro del experimento.

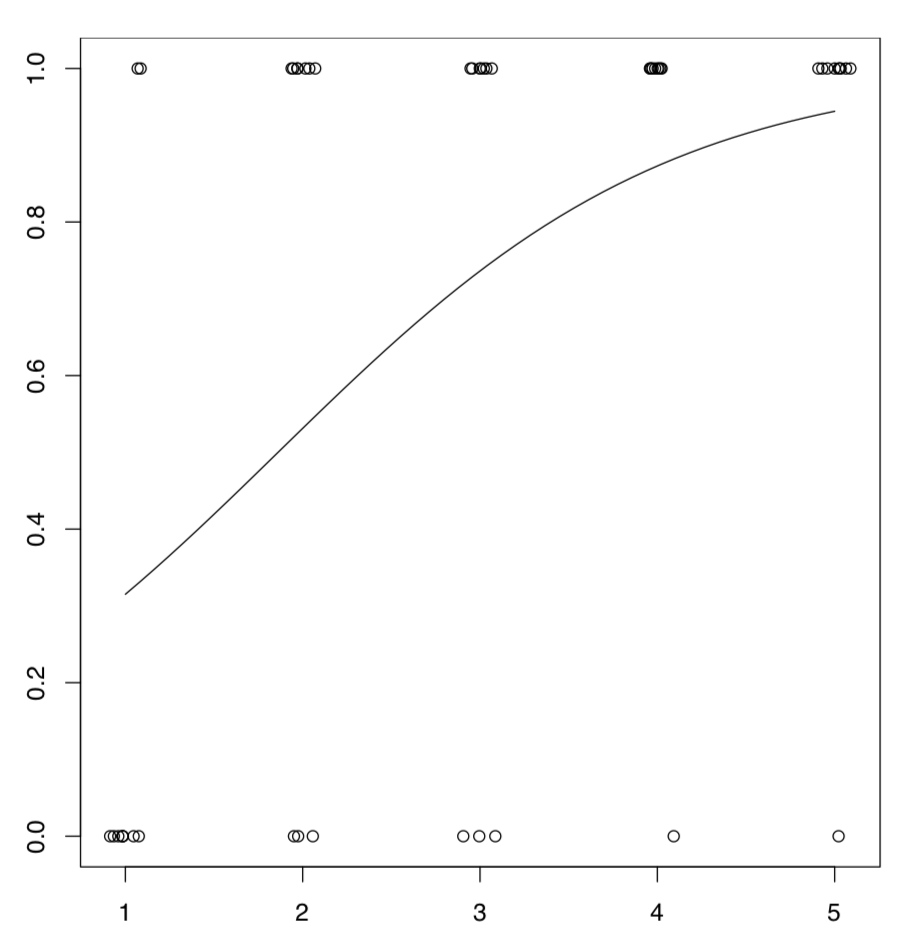
    Es posible representar gráficamente el modelo logístico (Figura\(\PageIndex{5}\)):

    Código\(\PageIndex{27}\) (R):

    seeing <- read.table("data/seeing.txt")
seeing.logit <- glm(V3 ~ V2, family=binomial, data=seeing)
tries <- seq(1, 5, length=50) # exactly 50 numbers from 1 to 5
seeing.p <- predict(seeing.logit, list(V2=tries), type="response")
plot(V3 ~ jitter(V2, amount=.1), data=seeing, xlab="", ylab="")
lines(tries, seeing.p)

    Usamos la función predict () para calcular las probabilidades de éxito para intentos no existentes, y también agregamos pequeño ruido aleatorio con función jitter () para evitar la superposición.

    Respuesta a las preguntas de enebro. Comprobar archivo, cargarlo, verificar el objeto:

    Código\(\PageIndex{28}\) (R):

    jj <- read.table( "http://ashipunov.info/shipunov/open/juniperus.txt", h=TRUE)
jj$LOC <- factor(jj$LOC, labels=paste0("loc", levels(jj$LOC)))
str(jj) # asmisc.r

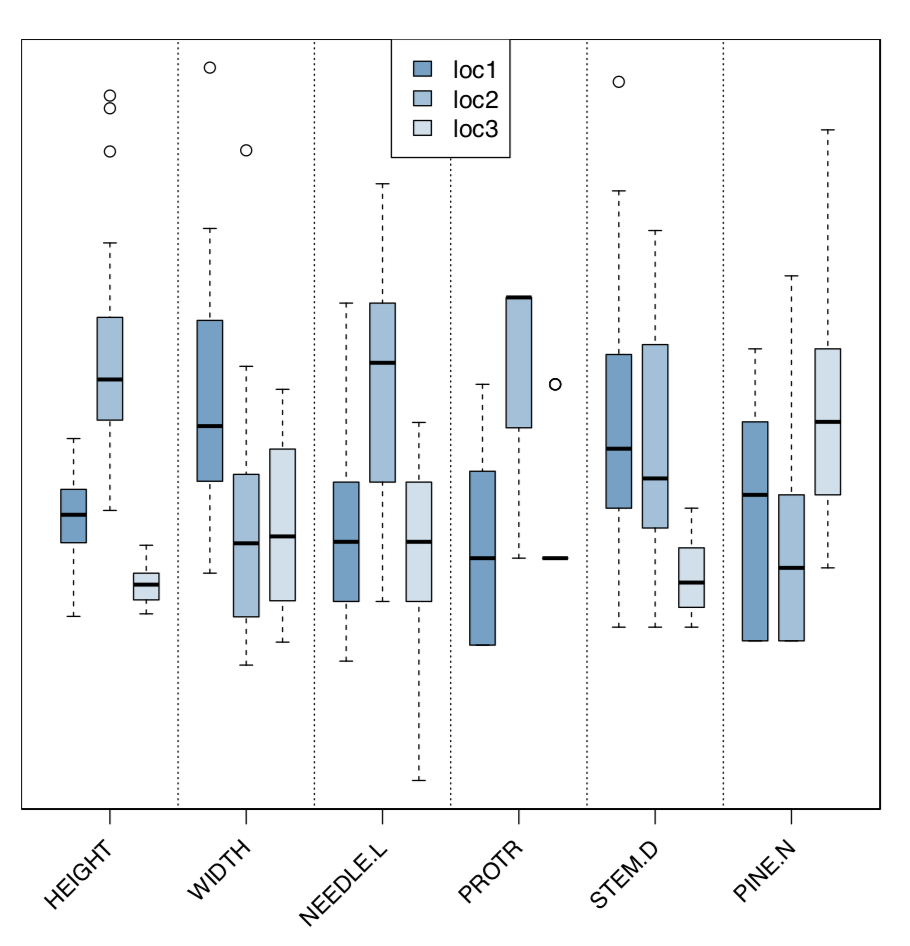
    Analizar gráficamente los caracteres morfológicos y ecológicos (Figura\(\PageIndex{6}\)):

    Screen Shot 2019-01-22 en 1.14.43 AM.png
    Figura Representación\(\PageIndex{5}\) gráfica del modelo logístico.

    Código\(\PageIndex{29}\) (R):

    jj <- read.table( "http://ashipunov.info/shipunov/open/juniperus.txt", h=TRUE)
j.cols <- colorRampPalette(c("steelblue", "white"))(5)[2:4]
boxplot(jj[, 2:7], jj$LOC, legpos="top", boxcols=j.cols) # asmisc.r

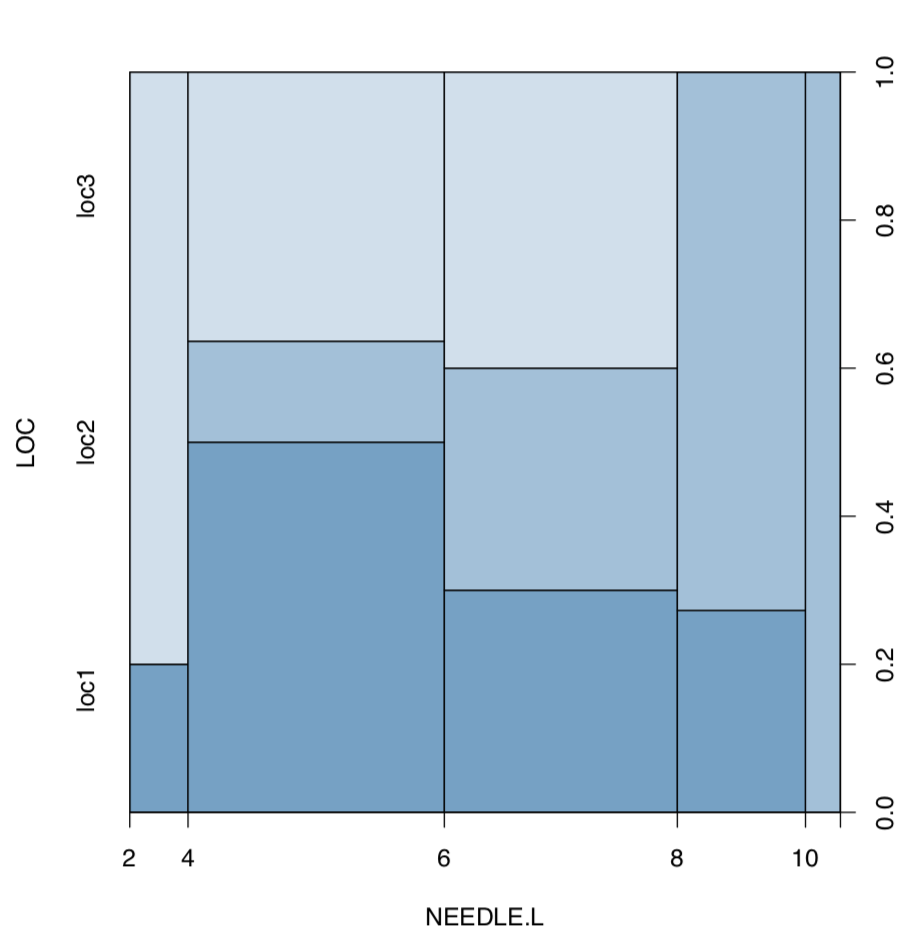
    Ahora trazar la longitud de las agujas contra la ubicación (Figura\(\PageIndex{7}\)):

    Código\(\PageIndex{30}\) (R):

    jj <- read.table( "http://ashipunov.info/shipunov/open/juniperus.txt", h=TRUE)
j.cols <- colorRampPalette(c("steelblue", "white"))(5)[2:4]
spineplot(LOC ~ NEEDLE.L, data=jj, col=j.cols)

    (Como ve, la gráfica de columna vertebral funciona con datos de medición).

    Dado que hay un carácter de medición y varias ubicaciones, la más adecuada es la aproximación similar a la de Anova. Primero tenemos que verificar las suposiciones:

    Código\(\PageIndex{31}\) (R):

    Normality <- function(a) {ifelse(shapiro.test(a)$p.value < 0.05, "NOT NORMAL", "NORMAL")}
jj <- read.table( "http://ashipunov.info/shipunov/open/juniperus.txt", h=TRUE)
Normality(jj$NEEDLE.L)
tapply(jj$NEEDLE.L, jj$LOC, var)
bartlett.test(NEEDLE.L ~ LOC, data=jj)
    Screen Shot 2019-01-22 en 1.23.14 AM.png
    Las\(\PageIndex{6}\) gráficas de caja de la Figura muestran la distribución de las mediciones entre las poblaciones de enebro. Dado que la variación no es homogénea, la prueba unidireccional con prueba t de pares post hoc es la mejor :

    Código\(\PageIndex{32}\) (R):

    jj <- read.table( "http://ashipunov.info/shipunov/open/juniperus.txt", h=TRUE)
oneway.test(NEEDLE.L ~ LOC, data=jj)
(eta.squared <-summary(lm(NEEDLE.L ~ LOC, data=jj))$adj.r.squared)
pairwise.t.test(jj$NEEDLE.L, jj$LOC)
    Screen Shot 2019-01-22 en 1.24.55 AM.png
    Figura Gráfica de\(\PageIndex{7}\) columna vertebral: localidad vs. longitud de aguja de enebros.

    (Obsérvese cómo calculamos eta-cuadrado, el tamaño del efecto de ANOVA. Como ves, esto podría hacerse a través del modelo lineal.)

    Hay diferencia significativa entre la segunda y otras dos ubicaciones.

    Y al segundo problema. Primero, hacemos una nueva variable basada en la expresión lógica de diferencias de caracteres:

    Código\(\PageIndex{33}\) (R):

    jj <- read.table( "http://ashipunov.info/shipunov/open/juniperus.txt", h=TRUE)
is.sibirica <- with(jj, (NEEDLE.L < 8 & HEIGHT < 100))
sibirica <- factor(is.sibirica, labels=c("communis", "sibirica"))
summary(sibirica)

    Hay ambas “especies” en los datos. Ahora, trazamos densidad condicional y analizamos regresión logística:

    Código\(\PageIndex{34}\) (R):

    jj <- read.table( "http://ashipunov.info/shipunov/open/juniperus.txt", h=TRUE)
is.sibirica <- with(jj, (NEEDLE.L < 8 & HEIGHT < 100))
sibirica <- factor(is.sibirica, labels=c("communis", "sibirica"))
cdplot(sibirica ~ PINE.N, data=jj, col=j.cols[c(1, 3)])
summary(glm(sibirica ~ PINE.N, data=jj, family=binomial))
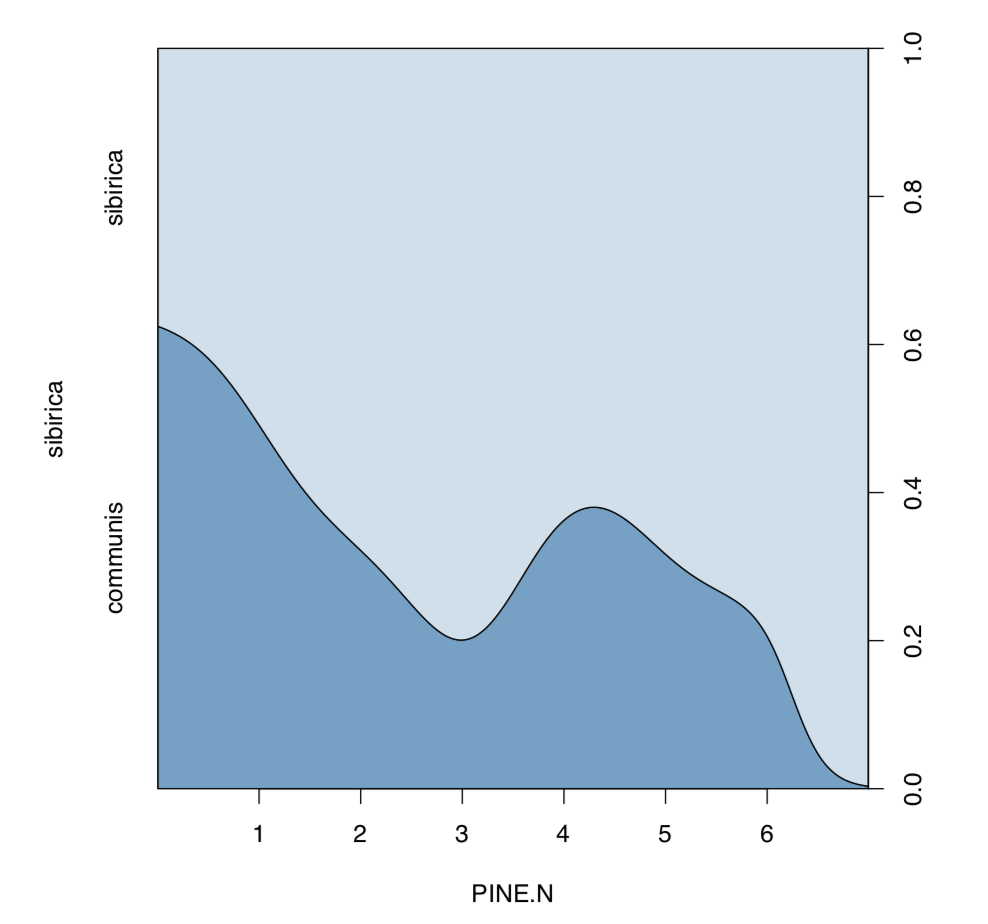
    Screen Shot 2019-01-22 en 1.26.47 AM.png
    Figura Densidad\(\PageIndex{8}\) condicional de ser Juniperus sibirica con presencia de algunos pinos.

    La gráfica de densidad condicional (Figura\(\PageIndex{8}\)) muestra una tendencia aparente y el resumen del modelo genera significancia para el coeficiente de pendiente.

    En la página siguiente, hay una tabla (Tabla\(\PageIndex{1}\)) con una clave que podría ayudar a elegir el método inferencial correcto si se conoce el número de muestras y el tipo de los datos.

    Tipo de datos Una variable Dos variables Muchas variables
    Medición, normalmente distribuida prueba t

    Diferencia: prueba t (emparejada y no emparejada), prueba F (escala)

    Tamaño del efecto: d de Cohen, K de Lyobishchev

    Relación: correlación, modelos lineales

    Modelos lineales, ANOVA, prueba unidireccional, prueba Bartlett (escala)

    Post hoc: prueba de pares, Tukey HSD

    Tamaño del efecto: R-cuadrado
    Medición y clasificación Prueba de Wilcoxon, prueba Shapiro-Wilk

    Diferencia: prueba de Wilcoxon (emparejado y no emparejado), prueba de signo, prueba irder de rango robusto, prueba de Ansari Bradley (escala)

    Tamaño del efecto: Delta del acantilado, K de Lyobishchev

    Relación: correlación no paramétrica

    Modelos lineales, LOESS, prueba de Kruskal-Wallis, prueba de Friedman, prueba de Fligner-Killeen (escala)

    Post hoc: prueba de Wilcoxon por pares, prueba de orden de rango robusta por pares

    Tamaño del efecto: R-cuadrado
    Categórico Prueba de proporciones de una muestra, prueba de bondad de ajuste

    Asociación: prueba de Chi-cuadrado, prueba exacta de Fisher, prueba de proporciones, prueba G, prueba de McNemar (pareado)

    Tamaño del efecto: V de Cramer, T de Tschuprow, ratio de probabilidades

    Pruebas de asociación (ver a la izquierda); modelos lineales generalizados de familia binomial (= regresión logística)

    Post hoc: prueba de mesa por pares

    Tabla\(\PageIndex{1}\) Clave de los métodos estadísticos inferenciales más importantes (excepto multivariantes). Después de acotar la búsqueda con un par de métodos, proceda al texto principal.

    This page titled 6.4: Respuestas a los ejercicios is shared under a Public Domain license and was authored, remixed, and/or curated by Alexey Shipunov via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.