3.2: Medidas de propagación
- Page ID
- 149651
La variabilidad es una idea importante en la estadística. Si tuvieras que medir la altura de todos en tu salón de clases, cada observación te da un valor diferente. Eso significa que no todos los estudiantes tienen la misma altura. Así, existe variabilidad en las alturas de las personas. Si tuvieras que tomar una muestra del nivel de ingresos de las personas en un pueblo, cada muestra te da información diferente. También hay variabilidad entre muestras. La variabilidad describe cómo se distribuyen los datos. Si los datos están muy cerca unos de otros, entonces hay poca variabilidad. Si los datos están muy dispersos, entonces hay una alta variabilidad. ¿Cómo se mide la variabilidad? Sería bueno tener un número que lo mida. En esta sección se describirán algunas de las diferentes medidas de variabilidad, también conocidas como variación.
En Ejemplo\(\PageIndex{1}\), se calculó que el peso promedio de un gato era de 8.02 libras. ¿Cuánto te dice esto del peso de todos los gatos? ¿Se puede decir si la mayoría de los pesos estaban cerca de 8.02 o los pesos estaban realmente distribuidos? ¿Cuáles son el peso más alto y el peso más bajo? Todo lo que sabes es que el centro de los pesos es de 8.02 libras. Necesitas más información.
Definición\(\PageIndex{1}\)
El rango de un conjunto de datos es la diferencia entre los valores de datos más altos y los más bajos (o valores máximos y mínimos).
\[\begin{align*} \text{Range} &= \text{highest value} - \text{lowest value} \\[4pt] &= \text{maximum value} - \text{minimum value} \end{align*}\]
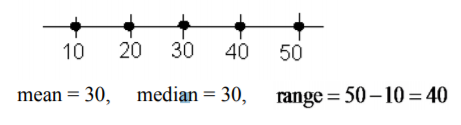
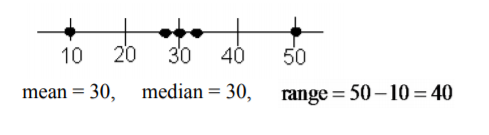
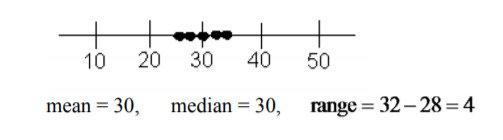
Ejemplo\(\PageIndex{1}\): Finding the Range
Mira los siguientes tres conjuntos de datos. Encuentra la gama de cada uno de estos.
- \(10, 20, 30, 40, 50\)
- \(10, 29, 30, 31, 50\)
- \(28, 29, 30, 31, 32\)
Solución
a.
.png)
b.
.png)
c.
.png)
Con base en la media, mediana y rango en Ejemplo\(\PageIndex{1}\), las dos primeras distribuciones son las mismas, pero se puede ver en las gráficas que son diferentes. En el Ejemplo\(\PageIndex{1}\) a los datos se distribuyen por igual. En el Ejemplo\(\PageIndex{1}\) b los datos tienen un clump en el medio y un solo valor en cada extremo. La media y la mediana son las mismas para el Ejemplo\(\PageIndex{1}\) c pero el rango es muy diferente. Todos los datos se agrupan en el medio.
El rango realmente no proporciona una imagen muy precisa de la variabilidad. Se necesita una mejor manera de describir cómo se distribuyen los datos. En lugar de mirar la distancia el valor más alto es desde el más bajo ¿qué tal si se mira a la distancia cada valor es de la media? Esta distancia se llama la desviación.
Ejemplo\(\PageIndex{2}\): Finding the Deviations
Supongamos que un veterinario quiere analizar los pesos de los gatos. Los pesos (en libras) de cinco gatos son 6.8, 8.2, 7.5, 9.4 y 8.2. Encuentra la desviación para cada uno de los valores de datos.
Solución
Variable:\(x=\) peso de un gato
La media para este conjunto de datos es\(\overline{x}=8.02\) libras.
| \(x\) | \(x-\overline{x}\) |
|---|---|
| \ (x\) ">6.8 | \ (x-\ overline {x}\) ">6.8-8.02 = -1.22 |
| \ (x\) ">8.2 | \ (x-\ overline {x}\) ">8.2-8.02=0.18 |
| \ (x\) ">7.5 | \ (x-\ overline {x}\) ">7.5-8.02=-0.52 |
| \ (x\) ">9.4 | \ (x-\ overline {x}\) ">9.4-8.02=1.38 |
| \ (x\) ">8.2 | \ (x-\ overline {x}\) ">8.2-8.02=0.18 |
Ahora es posible que desee promediar la desviación, por lo que debe sumar las desviaciones juntas.
| \(x\) | \(x-\overline{x}\) |
|---|---|
| \ (x\) ">6.8 | \ (x-\ overline {x}\) ">6.8-8.02 = -1.22 |
| \ (x\) ">8.2 | \ (x-\ overline {x}\) ">8.2-8.02=0.18 |
| \ (x\) ">7.5 | \ (x-\ overline {x}\) ">7.5-8.02=-0.52 |
| \ (x\) ">9.4 | \ (x-\ overline {x}\) ">9.4-8.02=1.38 |
| \ (x\) ">8.2 | \ (x-\ overline {x}\) ">8.2-8.02=0.18 |
| \ (x\) ">Total | \ (x-\ overline {x}\) ">0 |
Esto no puede estar bien. La distancia promedio desde la media no puede ser 0. La razón por la que se suma a 0 es porque hay algunos valores positivos y negativos. Necesitas deshacerte de los signos negativos. ¿Cómo puedes hacer eso? Podrías cuadrar cada desviación.
| \(x\) | \(x-\overline{x}\) | \((x-\overline{x})^{2}\) |
|---|---|---|
| \ (x\) ">6.8 | \ (x-\ overline {x}\) ">6.8-8.02 = -1.22 | \ ((x-\ overline {x}) ^ {2}\) ">1.4884 |
| \ (x\) ">8.2 | \ (x-\ overline {x}\) ">8.2-8.02=0.18 | \ ((x-\ overline {x}) ^ {2}\) ">0.0324 |
| \ (x\) ">7.5 | \ (x-\ overline {x}\) ">7.5-8.02=-0.52 | \ ((x-\ overline {x}) ^ {2}\) ">0.2704 |
| \ (x\) ">9.4 | \ (x-\ overline {x}\) ">9.4-8.02=1.38 | \ ((x-\ overline {x}) ^ {2}\) ">1.9044 |
| \ (x\) ">8.2 | \ (x-\ overline {x}\) ">8.2-8.02=0.18 | \ ((x-\ overline {x}) ^ {2}\) ">0.0324 |
| \ (x\) ">Total | \ (x-\ overline {x}\) ">0 | \ ((x-\ overline {x}) ^ {2}\) ">3.728 |
Ahora promedia el total de las desviaciones cuadradas. Lo único es que en las estadísticas hay un promedio extraño aquí. En lugar de dividir por el número de valores de datos se divide por el número de valores de datos menos 1. En este caso tendrías
\(s^{2}=\dfrac{3.728}{5-1}=\dfrac{3.728}{4}=0.932 \text { pounds }^{2}\)
Observe que esto se denota como\(s^{2}\). Esto se llama varianza y es una medida de la distancia cuadrada promedio desde la media. Si ahora tomas la raíz cuadrada, obtendrás la distancia promedio de la media. Esto se llama la desviación estándar, y se denota con la letra\(s\).
\(s=\sqrt{.932} \approx 0.965\)libras
La desviación estándar es la distancia promedio (media) de un punto de datos a la media. Se puede pensar en cuánto difiere un punto de datos típico de la media.
Definición\(\PageIndex{2}\): Sample Variance
La fórmula de varianza muestral:
\(s^{2}=\dfrac{\sum(x-\overline{x})^{2}}{n-1}\)
donde\(\overline{x}\) es la media de la muestra,\(n\) es el tamaño de la muestra, y\(\sum\) medias para encontrar la suma.
Definición\(\PageIndex{3}\): Sample Standard Deviation
La fórmula de desviación estándar de la muestra:
\(s=\sqrt{s^{2}}=\sqrt{\dfrac{\sum(x-\overline{x})^{2}}{n-1}}\)
El\(n-1\) de abajo tiene que ver con un concepto llamado grados de libertad. Básicamente, hace que la desviación estándar de la muestra sea una mejor aproximación de la desviación estándar de la población.
Definición\(\PageIndex{4}\): Population Variance
La fórmula de varianza poblacional:
\(\sigma^{2}=\dfrac{\sum(x-\mu)^{2}}{N}\)
donde\(\sigma\) es la letra griega sigma y\(\sigma^{2}\) representa la varianza poblacional,\(\mu\) es la media poblacional, y N es el tamaño de la población.
Definición\(\PageIndex{5}\): Population Standard Deviation
La fórmula de desviación estándar poblacional:
\(\sigma=\sqrt{\sigma^{2}}=\sqrt{\dfrac{\sum(x-\mu)^{2}}{N}}\)
Nota
La suma de las desviaciones siempre debe ser 0. Si no lo es, entonces es porque redondeaste, usaste la mediana en lugar de la media, o cometiste un error. Trate de no redondear demasiado en los cálculos para la desviación estándar ya que cada redondeo causa un ligero error
Ejemplo\(\PageIndex{3}\): Finding the Standard Deviation
Supongamos que un directivo quiere probar dos nuevos programas de capacitación. Selecciona al azar a 5 personas por cada tipo de entrenamiento y mide el tiempo que lleva completar una tarea después del entrenamiento. Los tiempos para ambos entrenamientos están en Ejemplo\(\PageIndex{4}\). ¿Qué método de entrenamiento es mejor?
| Entrenamiento 1 | 56 | 75 | 48 | 63 | 59 |
| Entrenamiento 2 | 60 | 58 | 66 | 59 | 58 |
Solución
Es importante que definas qué es cada variable ya que hay dos de ellas.
Variable 1:\(X_{1}=\) productividad desde el entrenamiento 1
Variable 2:\(X_{2}=\) productividad del entrenamiento 2
Para responder qué método de entrenamiento mejor, primero necesitas algunas estadísticas descriptivas. Comience con la media para cada muestra.
\(\overline{x}_{1}=\dfrac{56+75+48+63+59}{5}=60.2\)minutos
\(\overline{x}_{2}=\dfrac{60+58+66+59+58}{5}=60.2\)minutos
Dado que ambos medios son los mismos valores, no se puede responder a la pregunta sobre cuál es mejor. Ahora calcule la desviación estándar para cada muestra.
| \(x_{1}\) | \(x_{1}-\overline{x}_{1}\) | \(\left(x_{1}-\overline{x}_{1}\right)^{2}\) |
|---|---|---|
| \ (x_ {1}\) ">56 | \ (x_ {1} -\ overline {x} _ {1}\) ">-4.2 | \ (\ izquierda (x_ {1} -\ overline {x} _ {1}\ derecha) ^ {2}\) ">17.64 |
| \ (x_ {1}\) ">75 | \ (x_ {1} -\ overline {x} _ {1}\) ">14.8 | \ (\ izquierda (x_ {1} -\ overline {x} _ {1}\ derecha) ^ {2}\) ">219.04 |
| \ (x_ {1}\) ">48 | \ (x_ {1} -\ overline {x} _ {1}\) ">-12.2 | \ (\ izquierda (x_ {1} -\ overline {x} _ {1}\ derecha) ^ {2}\) ">148.84 |
| \ (x_ {1}\) ">63 | \ (x_ {1} -\ overline {x} _ {1}\) ">2.8 | \ (\ izquierda (x_ {1} -\ overline {x} _ {1}\ derecha) ^ {2}\) ">7.84 |
| \ (x_ {1}\) ">59 | \ (x_ {1} -\ overline {x} _ {1}\) ">-1.2 | \ (\ izquierda (x_ {1} -\ overline {x} _ {1}\ derecha) ^ {2}\) ">1.44 |
| \ (x_ {1}\) ">Total | \ (x_ {1} -\ overline {x} _ {1}\) ">0 | \ (\ izquierda (x_ {1} -\ overline {x} _ {1}\ derecha) ^ {2}\) ">394.8 |
| \(x_{2}\) | \(x_{2}-\overline{x}_{2}\) | \(\left(x_{2}-\overline{x}_{2}\right)^{2}\) |
|---|---|---|
| \ (x_ {2}\) ">60 | \ (x_ {2} -\ overline {x} _ {2}\) ">-0.2 | \ (\ izquierda (x_ {2} -\ overline {x} _ {2}\ derecha) ^ {2}\) ">0.04 |
| \ (x_ {2}\) ">58 | \ (x_ {2} -\ overline {x} _ {2}\) ">-2.2 | \ (\ izquierda (x_ {2} -\ overline {x} _ {2}\ derecha) ^ {2}\) ">4.84 |
| \ (x_ {2}\) ">66 | \ (x_ {2} -\ overline {x} _ {2}\) ">5.8 | \ (\ izquierda (x_ {2} -\ overline {x} _ {2}\ derecha) ^ {2}\) ">33.64 |
| \ (x_ {2}\) ">59 | \ (x_ {2} -\ overline {x} _ {2}\) ">-1.2 | \ (\ izquierda (x_ {2} -\ overline {x} _ {2}\ derecha) ^ {2}\) ">1.44 |
| \ (x_ {2}\) ">58 | \ (x_ {2} -\ overline {x} _ {2}\) ">-2.2 | \ (\ izquierda (x_ {2} -\ overline {x} _ {2}\ derecha) ^ {2}\) ">4.84 |
| \ (x_ {2}\) ">Total | \ (x_ {2} -\ overline {x} _ {2}\) ">0 | \ (\ izquierda (x_ {2} -\ overline {x} _ {2}\ derecha) ^ {2}\) ">44.8 |
La varianza para cada muestra es:
\(s_{1}^{2}=\dfrac{394.8}{5-1}=98.7 \text { minutes }^{2}\)
\(s_{2}^{2}=\dfrac{44.8}{5-1}=11.2 \text { minutes }^{2}\)
Las desviaciones estándar son:
\(s_{1}=\sqrt{98.7} \approx 9.93\)minutos
\(s_{2}=\sqrt{11.2} \approx 3.35\)minutos
A partir de las desviaciones estándar, el segundo entrenamiento parecía ser el mejor entrenamiento ya que los datos están menos dispersos. Esto quiere decir que es más consistente. Sería mejor para los directivos en este caso contar con un programa de capacitación que produzca resultados más consistentes para que sepan qué esperar del tiempo que lleva completar la tarea.
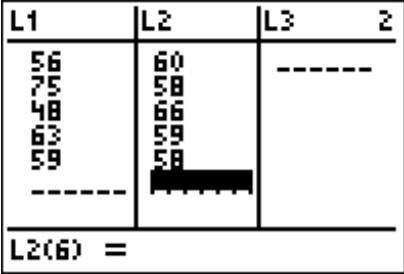
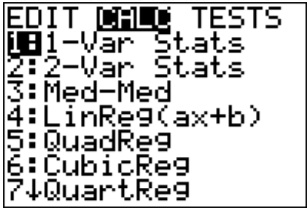
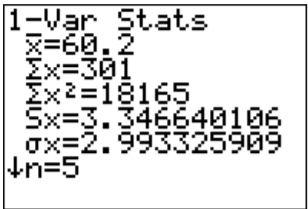
Se pueden hacer los cálculos para las estadísticas descriptivas utilizando la tecnología. El procedimiento para calcular la media muestral (\(\overline{x}) \)y la desviación estándar de la muestra (\(s_{x}\)) para\(X_{2}\) en el Ejemplo\(\PageIndex{3}\) sobre el TI-83/84 se encuentra en las Figuras 3.2.1 a 3.2.4 (el procedimiento es el mismo para\(X_{1}\)). Ten en cuenta que la calculadora te da la desviación estándar de la población (\(\sigma_{x}\)) porque no sabe si los datos que ingresas son una población o una muestra. Debes decidir qué valor necesitas usar, en función de si tienes una población o muestra. En casi todos los casos se tiene una muestra y se va a utilizar\(s_{x}\). Además, la calculadora utiliza la notación\(s_{x}\) de en lugar de solo\(s\). Es sólo una manera de denotar la información. Primero debes entrar en el menú STAT, y luego Editar. Esto te permitirá escribir tus datos (ver Figura\(\PageIndex{1}\)).
.png)
Una vez que tenga los datos en la calculadora, vuelva al menú STAT, pase a CALC y luego elija Estadísticas 1-Var (ver Figura\(\PageIndex{2}\)). La calculadora ahora pondrá 1-Var Stats en la pantalla principal. Ahora escriba L2 (2do botón y 2) y luego presione ENTRAR. (Tenga en cuenta que si tiene el sistema operativo más nuevo en el TI-84, entonces el procedimiento es ligeramente diferente). Los resultados de la calculadora están en la Figura\(\PageIndex{4}\).
.png)
.png)
.png)
Los procesos para encontrar la media, mediana, rango, desviación estándar y varianza en R son los siguientes:
variable<-c (escriba sus datos)
Para encontrar la media, use mean (variable)
Para encontrar la mediana, use median (variable)
Para encontrar el rango, use range (variable). Después encuentra máximo — mínimo.
Para encontrar la desviación estándar, use sd (variable)
Para encontrar la varianza, use var (variable)
Para el segundo conjunto de datos en Ejemplo\(\PageIndex{3}\), los comandos y resultados serían
productividad_2<-c (60, 58, 66, 59, 58)
media (productividad_2)
[1] 60,2
mediana (productividad_2)
[1] 59
rango (productividad_2)
[1] 58 66
sd (productividad_2)
[1] 3.34664
var ( productividad_2)
[1] 11.2
En general, una desviación estándar “pequeña” significa que los datos están muy juntos (más consistentes) y una desviación estándar “grande” significa que los datos están dispersos (menos consistentes). A veces quieres datos consistentes y a veces no. Como ejemplo si estás haciendo pernos, quieres que las longitudes sean muy consistentes por lo que quieres una pequeña desviación estándar. Si estás administrando una prueba para ver quién puede ser piloto, quieres una gran desviación estándar para que puedas saber quiénes son los buenos pilotos y quiénes son los malos.
¿Qué significan “pequeño” y “grande”? A un ciclistas cuya velocidad promedio es de 20 mph, s = 20 mph es enorme. A un avión cuya velocidad promedio es de 500 mph, s = 20 mph no es nada. El “tamaño” de la variación depende del tamaño de los números en el problema y de la media. Otra situación en la que puedes determinar si una desviación estándar es pequeña o grande es cuando estás comparando dos muestras diferentes como en el ejemplo #3 .2.3. Una muestra con una desviación estándar menor es más consistente que una muestra con una desviación estándar mayor.
Muchos otros libros y autores enfatizan que existe una fórmula computacional para calcular la desviación estándar. Sin embargo, esta fórmula no te da una idea de qué es la desviación estándar y qué estás haciendo. Sólo es bueno para hacer los cálculos rápidamente. Se remonta a los días en que las desviaciones estándar se calculaban a mano, y la persona necesitaba una forma rápida de calcular la desviación estándar. Es una fórmula arcaica que este autor está tratando de erradicarla. Ya no es necesario, ya que la mayoría de las calculadoras y computadoras harán los cálculos por ti con tanto significado como le da esta fórmula. Se sugiere que nunca lo uses. Si quieres entender lo que está haciendo la desviación estándar, entonces debes usar la fórmula de definición. Si quieres una respuesta rápida, usa una computadora o calculadora.
Uso de Desviación Estándar
Uno de los usos de la desviación estándar es describir cómo se distribuye una población usando el Teorema de Chebyshev. Este teorema funciona para cualquier distribución, ya sea sesgada, simétrica, bimodal o cualquier otra forma. Te da una idea de cuántos datos son una cierta distancia a cada lado de la media.
Definición\(\PageIndex{6}\): Chebyshev's Theorem
Para cualquier conjunto de datos:
- Al menos 75% de los datos caen en el intervalo de\(\mu-2 \sigma \text { to } \mu+2 \sigma\).
- Al menos 88.9% de los datos caen en el intervalo de\(\mu-3 \sigma \text { to } \mu+3 \sigma\).
- Al menos 93.8% de los datos caen en el intervalo de\(\mu-4 \sigma \text { to } \mu+4 \sigma\).
Ejemplo\(\PageIndex{4}\): Using Chebyshev's Theorem
La Oficina Meteorológica de Estados Unidos ha proporcionado la información en Ejemplo\(\PageIndex{7}\) sobre el número anual total de tornados reportados fuertes a violentos (F3+) en Estados Unidos para los años 1954 a 2012. (“Climatología de tornados de Estados Unidos”, 17).
| 46 | 47 | 31 | 41 | 24 | 56 | 56 | 23 | 31 | 59 |
| 39 | 70 | 73 | 85 | 33 | 38 | 45 | 39 | 35 | 22 |
| 51 | 39 | 51 | 131 | 37 | 24 | 57 | 42 | 28 | 45 |
| 98 | 35 | 54 | 45 | 30 | 15 | 35 | 64 | 21 | 84 |
| 40 | 51 | 44 | 62 | 65 | 27 | 34 | 23 | 32 | 28 |
| 41 | 98 | 82 | 47 | 62 | 21 | 31 | 29 | 32 |
- Usa el teorema de Chebyshev para encontrar un intervalo centrado en el número medio anual de tornados fuertes a violentos (F3+) en el que esperarías que caiga al menos el 75% de los años.
- Usa el teorema de Chebyshev para encontrar un intervalo centrado en el número medio anual de tornados fuertes a violentos (F3+) en el que esperarías que caigan al menos 88.9% de los años.
Solución
a. variable:\(x =\) número de tornados fuertes o violentos (F3+) El teorema de Chebyshev dice que al menos 75% de los datos caerán en el intervalo de\(\mu-2 \sigma\) a\(\mu+2 \sigma\).
No se tiene la población, por lo que es necesario estimar la media poblacional y la desviación estándar utilizando la media muestral y la desviación estándar. Puede encontrar la media de la muestra y la desviación estándar utilizando la tecnología:
\(\overline{x} \approx 46.24, s \approx 22.18\)
Entonces,
\(\mu \approx 46.24, \sigma \approx 22.18\)
\(\mu-2 \sigma \text { to } \mu+2 \sigma\)
\(46.24-2(22.18) \text { to } 46.24+2(22.18)\)
\(46.24-44.36 \text { to } 46.24+44.36\)
\(1.88 \text { to } 90.60\)
Ya que no se puede tener número fraccional de tornados, redondear al número entero más cercano.
Al menos 75% de los años tienen entre 2 y 91 tornados fuertes a violentos (F3+). (En realidad, todos los valores de menos tres años caen en este intervalo, eso significa que\(\dfrac{56}{59} \approx 94.9 \%\) realmente caen en el intervalo.)
b. variable:\(x =\) número de tornados fuertes o violentos (F3+) El teorema de Chebyshev dice que al menos 88.9% de los datos caerán en el intervalo de\(\mu-3 \sigma\) a\(\mu+3 \sigma\).
\(\mu-3 \sigma \text { to } \mu+3 \sigma\)
\(46.24-3(22.18) \text { to } 46.24+3(22.18)\)
\(46.24-66.54 \text { to } 46.24+66.54\)
\(-20.30 \text { to } 112.78\)
Como no se puede tener número negativo de tornados, el límite inferior es en realidad 0. Ya que no se puede tener número fraccional de tornados, redondear al número entero más cercano.
Al menos 88.9% de los años tienen entre 0 y 113 tornados fuertes a violentos (F3+).
(En realidad, todos menos un año cae en este intervalo, eso significa que\(\dfrac{58}{59} \approx 98.3 \%\) realmente caen en el intervalo.)
El Teorema de Chebyshev dice que al menos 75% de los datos se encuentran dentro de dos desviaciones estándar de la media. Ese porcentaje es bastante alto. No hay muchos datos fuera de dos desviaciones estándar. Una regla que se puede seguir es que si un valor de datos está dentro de dos desviaciones estándar, entonces ese valor es un valor de datos común. Si el valor de los datos está fuera de dos desviaciones estándar de la media, ya sea por encima o por debajo, entonces el número es poco común. Incluso podría llamarse inusual. Un cálculo sencillo que puedes hacer para resolverlo es encontrar la diferencia entre el punto de datos y la media, y luego dividir esa respuesta por la desviación estándar. Como fórmula esto sería
\(\dfrac{x-\mu}{\sigma}\).
Si no conoces la media poblacional,\(\mu\), y la desviación estándar de la población\(\sigma\), entonces usa la media muestral\(\overline{x}\), y la desviación estándar de la muestra,\(s\), para estimar los valores de los parámetros poblacionales. Sin embargo, tenga en cuenta que el uso de la desviación estándar de la muestra puede no ser realmente muy preciso.
Ejemplo\(\PageIndex{5}\) determining if a value is unusual
- En 1974, había 131 tornados fuertes o violentos (F3+) en Estados Unidos. ¿Este valor es inusual? ¿Por qué o por qué no?
- En 1987, hubo 15 tornados fuertes o violentos (F3+) en Estados Unidos. ¿Este valor es inusual? ¿Por qué o por qué no?
Solución
a. Variable:\(x =\) número de tornados fuertes o violentos (F3+)
Para responder a esta pregunta, primero encuentra cuántas desviaciones estándar 131 es de la media. De Ejemplo\(\PageIndex{4}\), sabemos\(\mu \approx 46.24\) y\(\sigma \approx 22.18\). Para\(x = 131\),
\(\dfrac{x-\mu}{\sigma}=\dfrac{131-46.24}{22.18} \approx 3.82\)
Dado que este valor es más de 2, entonces es inusual tener 131 tornados fuertes o violentos (F3+) en un año.
b. Variable:\(x =\) número de tornados fuertes o violentos (F3+) Para esta pregunta\(x = 15\),
\(\dfrac{x-\mu}{\sigma}=\dfrac{15-46.24}{22.18} \approx-1.41\)
Dado que este valor está entre -2 y 2, entonces no es raro tener solo 15 tornados fuertes o violentos (F3+) en un año.
Tarea
Ejercicio\(\PageIndex{1}\)
- Los niveles de colesterol se recolectaron de los pacientes dos días después de sufrir un ataque al corazón (Ryan, Joiner & Ryan, Jr, 1985) y están en Ejemplo\(\PageIndex{8}\). Encuentre la media, mediana, rango, varianza y desviación estándar usando tecnología.
270 236 210 142 280 272 160 220 226 242 186 266 206 318 294 282 234 224 276 282 360 310 280 278 288 288 244 236 Tabla\(\PageIndex{8}\): Niveles de colesterol - Las longitudes (en kilómetros) de los ríos de la Isla Sur de Nueva Zelanda que fluyen hacia el Océano Pacífico se enumeran en Example\(\PageIndex{9}\) (Lee, 1994).
Tabla\(\PageIndex{9}\): Longitudes de ríos (km) que fluyen hacia el Océano Pacífico Río Longitud (km) Río Longitud (km) Clarence 209 Clutha 322 Conway 48 Taieri 288 Waiau 169 Shag 72 Hurunui 138 Kakanui 64 Waipara 64 Waitaki 209 Ashley 97 Waihao 64 Waimakariri 161 Pareora 56 Selwyn 95 Rangitata 121 Rakaia 145 Ohi 80 Ashburton 90 a. Encuentra la media y la mediana.
b. Encuentra la gama.
c. Encuentra la varianza y desviación estándar. - Las longitudes (en kilómetros) de los ríos de la Isla Sur de Nueva Zelanda que fluyen hacia el Océano Pacífico se enumeran en Example\(\PageIndex{9}\) (Lee, 1994).
Río Longitud (km) Río Longitud (km) Hollyford 76 Waimea 48 Cascade 64 Motueka 108 Arawhata 68 Takaka 72 Haast 64 Aorere 72 Karangarua 37 Heaphy 35 Cocinero 32 Karamea 80 Waiho 32 Mokihinui 56 Whataroa 51 Buller 177 Wanganui 56 Gris 121 Waitaha 40 Taramakau 80 Hokitika 64 Arahura 56 Cuadro\(\PageIndex{10}\): Longitudes de ríos (km) que fluyen al mar de Tasmania
a. Encuentra la media y mediana.
b. Encuentra la gama.
c. Encuentra la varianza y desviación estándar. - Eyeglassmatic fabrica anteojos para sus minoristas. Prueban para ver cuántas lentes defectuosas hicieron el periodo de tiempo del 1 de enero al 31 de marzo. Ejemplo\(\PageIndex{11}\) da el defecto y el número de defectos.
Tipo de defecto Número de defectos Rasguño 5865 Forma derecha - pequeña 4613 Descamado 1992 Eje incorrecto 1838 El chaflán está mal 1596 agrietamiento, grietas 1546 Forma incorrecta 1485 PD incorrecto 1398 Manchas y burbujas 1371 Altura incorrecta 1130 Forma derecha - grande 1105 Perdido en laboratorio 976 Manchas/Burbuja - pasante 976
Cuadro\(\PageIndex{11}\): Número de lentes defectuosos
a. Encuentra la media y mediana.
b. Encuentra la gama.
c. Encuentra la varianza y desviación estándar. - Los empleados de la empresa de impresión Print-O-Matic tienen salarios que están contenidos en Ejemplo\(\PageIndex{12}\). Encuentre la media, mediana, rango, varianza y desviación estándar usando tecnología.
Empleado Sueldo ($) Empleado Sueldo ($) CEO 272,500 Administración 66,346 Conductor 58,456 Ventas 109,739 CD74 100,702 Diseñador 90,090 CD65 57,380 Platinas 69,573 Embellecedor 73,877 Polar 75,526 Carpeta 65,270 ITEK 64,553 GTO 74,235 Mgmt 108,448 Gerente de Pre Prensa 108,448 Trabajo hecho a mano 52,718 Gerente de Pre Prensa/IT 98.837 Horizon 76,029 Pre Prensa/Artista Gráfico 75,311 Tabla\(\PageIndex{12}\): Salarios de los empleados de Print-O-Matic Printing Company - Imprint-O-Matic empresa de impresión gasta montos específicos en costos fijos cada mes. Los costos de esos costos fijos están en Ejemplo\(\PageIndex{13}\).
Tabla\(\PageIndex{13}\): Costos fijos para Imprint-O-Matic Printing Company Cargos mensuales Costo mensual ($) Cargos bancarios 482 Limpieza 2208 Computadora cara 2471 Pagos de arrendamiento 2656 Franqueo 2117 Uniformes 2600 a. Encuentra la media y la mediana.
b. Encuentra la gama.
c. Encuentra la varianza y desviación estándar. - Comparar los dos conjuntos de datos en los problemas 2 y 3 usando la media y la desviación estándar. Discutir cuál es la media más alta y cuál tiene una mayor dispersión de los datos.
- Ejemplo\(\PageIndex{14}\) contiene las frecuencias de pulso recolectadas de machos, que son no fumadores pero sí beben alcohol (“Pulso antes”, 2013). La frecuencia del pulso anterior es antes de que ejercitaran, y la frecuencia del pulso posterior se tomó después de que el sujeto corriera en su lugar durante un minuto. Compare los dos conjuntos de datos usando la media y la desviación estándar. Discutir cuál es la media más alta y cuál tiene una mayor dispersión de los datos.
Pulso antes Pulso después Pulso antes Pulso después 76 88 59 92 56 110 60 104 64 126 65 82 50 90 76 150 49 83 145 155 68 136 84 140 68 125 78 141 88 150 85 131 80 146 78 132 78 168 Tabla\(\PageIndex{14}\): Pulso de varones antes y después del ejercicio - Ejemplo\(\PageIndex{15}\) contiene las frecuencias de pulso recolectadas de hembras, que son no fumadoras pero sí beben alcohol (“Pulso antes”, 2013). La frecuencia del pulso anterior es antes de que ejercitaran, y la frecuencia del pulso posterior se tomó después de que el sujeto corriera en su lugar durante un minuto. Compare los dos conjuntos de datos usando la media y la desviación estándar. Discutir cuál es la media más alta y cuál tiene una mayor dispersión de los datos.
Pulso antes Pulso después Pulso antes Pulso después 96 176 92 120 82 150 70 96 86 150 75 130 72 115 70 119 78 129 70 95 90 160 68 84 88 120 47 136 71 125 64 120 66 89 70 98 76 132 74 168 70 120 85 130 Tabla\(\PageIndex{15}\): Pulso de las hembras antes y después del ejercicio - Para determinar si el Reiki es un método efectivo para tratar el dolor, se realizó un estudio piloto donde un terapeuta de Reiki certificado de segundo grado brindó tratamiento a voluntarios. El dolor se midió usando una escala visual analógica (VAS) inmediatamente antes y después del tratamiento de Reiki (Olson & Hanson, 1997) y los datos están en Ejemplo\(\PageIndex{16}\). Compare los dos conjuntos de datos usando la media y la desviación estándar. Discutir cuál es la media más alta y cuál tiene una mayor dispersión de los datos.
VAS antes VAS después VAS antes VAS después 6 3 5 1 2 1 1 0 2 0 6 4 9 1 6 1 3 0 4 4 3 2 4 1 4 1 7 6 5 2 2 1 2 2 4 3 3 0 8 8 Tabla\(\PageIndex{16}\): Medidas del dolor antes y después del tratamiento de Reiki - Ejemplo\(\PageIndex{17}\) contiene datos recopilados sobre el tiempo que toma en segundos de cada paso de juego en una partida de rugby. (“Tiempo de los pasajes”, 2013)
Tabla\(\PageIndex{17}\): Tiempos (en segundos) de jugadas de rugby 39.2 2.7 9.2 14.6 1.9 17.8 15.5 53.8 17.5 27.5 4.8 8.6 22.1 29.8 10.4 9.8 27.7 32.7 32 34.3 29.1 6.5 2.8 10.8 9.2 12.9 7.1 23.8 7.6 36.4 35.6 28.4 37.2 16.8 21.2 14.7 44.5 24.7 36.2 20.9 19.9 24.4 7.9 2.8 2.7 3.9 14.1 28.4 45.5 38 18.5 8.3 56.2 10.2 5.5 2.5 46.8 23.1 9.2 10.3 10.2 22 28.5 24 17.3 12.7 15.5 4 5.6 3.8 21.6 49.3 52.4 50.1 30.5 37.2 15 38.7 3.1 11 10 5 48.8 3.6 12.6 9.9 58.6 37.9 19.4 29.2 12.3 39.2 22.2 39.7 6.4 2.5 34 a. Utilizando la tecnología, encontrar la media y la desviación estándar.
b. Usa el teorema de Chebyshev para encontrar un intervalo centrado en los tiempos medios de cada paso de juego en el juego de rugby en el que esperarías que caigan al menos 75% de los tiempos.
c. Usa el teorema de Chebyshev para encontrar un intervalo centrado en los tiempos medios de cada paso de juego en el juego de rugby en el que esperarías que caigan al menos 88.9% de los tiempos. - Las cantidades anuales de lluvia (en milímetros) en Sydney, Australia, se encuentran en la tabla #3 .2.18 (“Máximo anual de,” 2013).
Tabla\(\PageIndex{18}\): Cantidades anuales de lluvia en Sydney, Australia 146.8 383 90.9 178.1 267.5 95.5 156.5 180 90.9 139.7 200.2 171.7 187.2 184.9 70.1 58 84.1 55.6 133.1 271.8 135.9 71.9 99.4 110.6 47.5 97.8 122.7 58.4 154.4 173.7 118.8 88 84.6 171.5 254.3 185.9 137.2 138.9 96.2 85 45.2 74.7 264.9 113.8 133.4 68.1 156.4 a. Utilizando la tecnología, encontrar la media y la desviación estándar.
b. use el teorema de Chebyshev para encontrar un intervalo centrado en las cantidades medias anuales de lluvia en Sydney, Australia, en el que se esperaría que al menos el 75% de las cantidades cayeran.
c. Usa el teorema de Chebyshev para encontrar un intervalo centrado en las cantidades medias anuales de lluvia en Sydney, Australia, en el que esperarías que caigan al menos 88.9% de las cantidades. - El número de muertes atribuidas a la radiación UV en los países africanos en el año 2002 se da en Ejemplo\(\PageIndex{19}\) (“Radiación UV: Burden”, 2013).
Tabla\(\PageIndex{19}\): Número de muertes por radiación UV 50 84 31 338 6 504 40 7 58 204 15 27 39 1 45 174 98 94 199 9 27 58 356 5 45 5 94 26 171 13 57 138 39 3 171 41 1177 102 123 433 35 40 456 125 a. Utilizando la tecnología, encontrar la media y la desviación estándar.
b. use el teorema de Chebyshev para encontrar un intervalo centrado en el número medio de muertes por radiación UV en el que se esperaría que al menos 75% de los números cayeran.
c. Usa el teorema de Chebyshev para encontrar un intervalo centrado en el número medio de muertes por radiación UV en el que se esperaría que al menos el 88.9% de los números cayeran. - El tiempo (en 1/50 segundos) entre pulsos sucesivos a lo largo de una fibra nerviosa (“Tiempo entre nervio”, 2013) se dan en Ejemplo\(\PageIndex{20}\).
Tabla\(\PageIndex{20}\): Tiempo (en 1/50 segundos) entre pulsos sucesivos 10.5 1.5 2.5 5.5 29.5 3 9 27.5 18.5 4.5 7 9.5 1 7 4.5 2.5 7.5 11.5 7.5 4 12 8 3 5.5 7.5 4.5 1.5 10.5 1 7 12 14.5 8 3.5 3.5 2 1 7.5 6 13 7.5 16.5 3 25.5 5.5 14 18 7 27.5 14 a. Utilizando la tecnología, encontrar la media y la desviación estándar.
b. Usa el teorema de Chebyshev para encontrar un intervalo centrado en el tiempo medio entre pulsos sucesivos a lo largo de una fibra nerviosa en el que esperarías que caigan al menos 75% de los tiempos.
c. Usa el teorema de Chebyshev para encontrar un intervalo centrado en el tiempo medio entre pulsos sucesivos a lo largo de una fibra nerviosa en el que esperarías que caigan al menos 88.9% de los tiempos. - Supongamos que un paso de juego en un juego de rugby toma 75.1 segundos. ¿Sería inusual que esto sucediera? Usa la media y desviación estándar que calculaste en el problema 11.
- Supongamos que Sydney, Australia recibió 300 mm de lluvia en un año. ¿Sería esto inusual? Usa la media y desviación estándar que calculaste en el problema 12.
- Supongamos que en un año determinado hubo 2257 muertes atribuidas a la radiación UV en un país africano. ¿Este valor es inusual? Usa la media y desviación estándar que calculaste en el problema 13.
- Supongamos que solo toma 2 (1/50 segundos) para pulsos sucesivos a lo largo de una fibra nerviosa. ¿Este valor es inusual? Usa la media y desviación estándar que calculaste en el problema 14.
- Contestar
-
1. media = 253.93, mediana = 268, rango = 218, varianza = 2276.29, st dev = 47.71
3. a. media = 67.68 km, mediana = 64 km, b. rango = 145 km, c. varianza = 1107.9416\(\mathrm{km}^{2}\), st dev = 33.29 km
5. media = $89.370.42, mediana = $75.311, rango = $219.782, varianza =2298639399, st dev = $47,944.13
7. Ver soluciones
9. \(\overline{x}_{1} \approx 75.45, s_{1} \approx 11.10, \overline{x}_{2} \approx 125.55, s_{2} \approx 24.72\)
11. a.\(\overline{x} \approx 21.24 \mathrm{sec}, s \approx 14.95 \mathrm{sec}\) b.\((-8.66 \mathrm{sec}, 51.14 \mathrm{sec})\) c.\((-23.61 \mathrm{sec}, 66.09 \mathrm{sec})\)
13. a.\(\overline{x} \approx 130.98, s \approx 205.44\) b.\((-279.90,541.86)\) c.\((-485.34,747.3)\)
15. 3.61
17. 10.35


