Saltar al contenido principal
LibreTexts Español

4.4: Técnicas de conteo

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    149775

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Hay momentos en que el espacio de muestra o espacio de eventos son muy grandes, que no es factible escribirlo. En ese caso, ayuda tener herramientas matemáticas para contar el tamaño del espacio de muestra y espacio de eventos. Estas herramientas se conocen como técnicas de conteo.

    Definición\(\PageIndex{1}\)

    Regla de multiplicación en técnicas de conteo

    Si la tarea 1 se puede hacer de \(m_{1}\)maneras, la tarea 2 se puede hacer \(m_{2}\)maneras, y así sucesivamente a la tarea n que se hace \(m_{n}\)maneras. Entonces el número de formas de hacer la tarea 1, 2,..., n juntas sería \(m_{1}^{*} m_{2}^{*} \stackrel{\Delta *}{r} m_{n}\).

    Ejemplo\(\PageIndex{1}\) multiplication rule in counting

    Un menú ofrece una selección de 3 ensaladas, 8 platos principales y 5 postres. ¿Cuántas comidas diferentes que consisten en una ensalada, un plato principal y un postre son posibles?

    Solución

    Hay tres tareas, escoger una ensalada, un plato principal y un postre. La tarea de ensalada se puede hacer de 3 maneras, la tarea del plato principal se puede hacer de 8 formas, y la tarea de postre se puede hacer de 5 maneras. Las formas de elegir una ensalada, plato principal y postre son

    \(\dfrac{3}{\text { salad }} \dfrac{8}{\text { main }} \dfrac{5}{\text { dessert }}=120\)diferentes comidas

    Ejemplo\(\PageIndex{2}\) Multiplication rule in counting

    ¿Cuántas “palabras” de tres letras se pueden hacer a partir de las letras a, b y c sin que se repitan letras? Una “palabra” es solo un grupo ordenado de letras. No tiene que ser una palabra real en un diccionario.

    Solución

    Hay tres tareas que se deben hacer en este caso. Las tareas son escoger la primera letra, luego la segunda letra, y luego la tercera letra. La primera tarea se puede hacer de 3 maneras ya que hay 3 letras. La segunda tarea se puede hacer de 2 maneras, ya que la primera tarea tomó una de las letras. La tercera tarea se puede hacer de 1 maneras, ya que la primera y la segunda tarea tomaron dos de las letras. Hay

    \(\dfrac{3}{\text { first letter }} * \dfrac{2}{\text { second letter }} * \dfrac{1}{\text { third letter }}\)

    Que es

    \(3^{*} 2^{*} 1=6\)

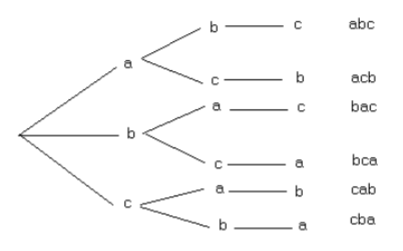
    También puedes ver esto en un diagrama de árbol:

    Captura de pantalla (72) .png
    Figura\(\PageIndex{1}\): Diagrama de árbol

    Entonces, hay 6 “palabras” diferentes.

    En Ejemplo\(\PageIndex{2}\), la solución se encontró por hallazgo\(3*2*1=6\). Muchos problemas de conteo implican multiplicar una lista de números decrecientes. A esto se le llama factorial. Hay un símbolo especial para esto y un botón especial en su calculadora.

    Definición\(\PageIndex{2}\)

    Factorial

    \(n !=n(n-1)(n-2) \cdots(3)(2)(1)\)

    Como ejemplo:

    \(5 !=5 * 4 * 3 * 2 * 1=120\)

    \(8 !=8 * 7 * 6 * 5 * 4 * 3 * 2 * 1=40320\)

    0 factorial se define como 0! =1 y 1 factorial se define como ¡1! =1.

    A veces está tratando de seleccionar r objetos de n objetos totales. El número de formas de hacerlo depende de si el orden que elijas los objetos r importa o si no lo hace.Como ejemplo si estás tratando de llamar a una persona por teléfono, tienes que tener su número en el orden correcto. De lo contrario, llamas a alguien que no querías decir. En este caso, importa el orden de los números. Sin embargo, si estaba recogiendo números aleatorios para la lotería, no importa qué número elija primero. Siempre y cuando tengas los mismos números que escoja la gente de la lotería, ganas. En este caso la orden no importa. Una permutación es un arreglo de artículos con un orden específico. Se utilizan permutaciones para contar artículos cuando el pedido importa. Cuando el pedido no importa usas combinaciones. Una combinación es un arreglo de artículos cuando el orden no es importante. Cuando haces un problema de conteo, lo primero que debes preguntarte es “¿importa el orden?”

    Definición\(\PageIndex{3}\)

    Fórmula de permutación

    Selección de r objetos de n objetos totales cuando el orden importa

    \(_{n} P_{r}=\dfrac{n !}{(n-r) !}\)

    Definición\(\PageIndex{4}\)

    Fórmula de combinación

    Elegir r objetos de n objetos totales cuando el orden no importa

    \(_{n} C_{r}=\dfrac{n !}{r !(n-r) !}\)

    Ejemplo\(\PageIndex{3}\) calculating the number of ways

    En un club con 15 miembros, ¿de cuántas maneras se puede elegir una pizarra de 3 oficiales compuesta por un presidente, vicepresidente y secretario/tesorero?

    Solución

    En este caso el orden importa. Si elige a la persona 1 para presidente, la persona 2 para el vicepresidente y la persona 3 para el secretario/tesorero, tendrías oficiales diferentes a los que elegieran a la persona 2 para presidente, la persona 1 para el vicepresidente y la persona 3 para la secretaria/tesorera. Este es un problema de permutación con n=15 y r=3.

    \(_{15} P_{3}=\dfrac{15 !}{(15-3) !}=\dfrac{15 !}{12 !}=2730\)

    Ejemplo\(\PageIndex{4}\) calculating the number of ways

    Supongamos que quieres elegir a 7 personas de entre 20 personas para que participen en una encuesta. ¿De cuántas maneras puedes hacer esto?

    Solución

    En este caso el pedido no importa, ya que solo quieres 7 personas. Esta es una combinación con n=20 y r=7.

    \(_{20} C_{7}=\dfrac{20 !}{7 !(20-7) !}=\dfrac{20 !}{7 ! 13 !}=77520\)

    La mayoría de las calculadoras tienen un botón factorial en ellas, y muchas tienen las funciones de combinación y permutación también. R tiene un comando de combinación.

    Testo

    Ejercicio\(\PageIndex{1}\)

    1. Vas a una cena benéfica, y necesitas decidir antes de la cena qué quieres para ensalada, plato principal y postre. Tienes 2 ensaladas diferentes para elegir, 3 platos principales y 5 postres. ¿Cuántas comidas diferentes hay disponibles?
    2. ¿Cuántos números de teléfono diferentes hay en el código de área 928?
    3. Estás abriendo una tienda de camisetas. Puedes tener mangas largas o mangas cortas, tres colores diferentes, cinco diseños diferentes y cuatro tamaños diferentes. ¿Cuántas camisas diferentes puedes hacer?
    4. La placa de California tiene un número seguido de tres letras seguidas de tres números. ¿Cuántas matrículas diferentes hay?
    5. Encuentra\(_{9} P_{4}\)
    6. Encuentra\(_{10} P_{6}\)
    7. Encuentra\(_{10} P_{5}\)
    8. Encuentra\(_{20} P_{4}\)
    9. Tienes un grupo de doce personas. Es necesario elegir entre los doce a un presidente, tesorero y secretario. ¿De cuántas maneras diferentes puedes hacer esto?
    10. Un equipo de beisbol tiene un roster de 25 hombres. Una orden de bateo tiene nueve personas. ¿Cuántas órdenes de bateo diferentes hay?
    11. Una urna contiene cinco bolas rojas, siete bolas amarillas y ocho bolas blancas. ¿De cuántas maneras diferentes puedes escoger dos bolas rojas?
    12. ¿De cuántas maneras puedes elegir a siete personas de un grupo de veinte?
    Contestar

    1. 30 comidas

    3. 120 playeras

    5. 3024

    7. 252

    9. 1320

    11. 10

    Fuentes de datos

    Muertes aborígenes bajo custodia. (2013, 26 de septiembre). Recuperado a partir de http://www.statsci.org/data/oz/custody.html

    Actividades de grupos de delfines. (2013, 26 de septiembre). Recuperado a partir de http://www.statsci.org/data/general/dolpacti.html

    Preferencias de autos. (2013, 26 de septiembre). Recuperado a partir de http://www.statsci.org/data/oz/carprefs.html

    Enciclopedia Titanica. (2013, 09 de noviembre). Recuperado de www.encyclopediatitanica.org/

    Lepra: Número de casos reportados por país. (2013, 04 de septiembre). Recuperado a partir de http://apps.who.int/gho/data/node.main.A1639

    Madison, J. (2013, 15 de octubre). Análisis de distribución de color de M&M. Recuperado a partir de http://joshmadison.com/2007/12/02/mm...tion-analysis/

    This page titled 4.4: Técnicas de conteo is shared under a CC BY-SA 4.0 license and was authored, remixed, and/or curated by Kathryn Kozak via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.