5.1: Conceptos básicos de las distribuciones de probabilidad
- Page ID
- 149717
Como recordatorio, una variable o lo que se llamará la variable aleatoria a partir de ahora, se representa con la letra x y representa una variable cuantitativa (numérica) que se mide u observa en un experimento.
También recuerde que existen diferentes tipos de variables cuantitativas, llamadas discretas o continuas. ¿Cuál es la diferencia entre datos discretos y continuos? Los datos discretos solo pueden tomar valores particulares en un rango. Los datos continuos pueden tomar cualquier valor en un rango. Los datos discretos generalmente surgen del conteo, mientras que los datos continuos generalmente surgen de la medición.
Ejemplos de cada
¿A qué altura se le da a una planta un nuevo fertilizante? Continuo. Esto es algo que se mide. ¿Cuántas pulgas hay en perros de pradera en una colonia? Discreta. Esto es algo que cuentas.
Si tienes una variable, y puedes encontrar una probabilidad asociada a esa variable, se llama variable aleatoria. En muchos casos la variable aleatoria es lo que estás midiendo, pero cuando se trata de variables aleatorias discretas, suele ser lo que estás contando. Entonces, para el ejemplo de qué tan alta es una planta dada un nuevo fertilizante, la variable aleatoria es la altura de la planta dada un nuevo fertilizante. Para el ejemplo de cuántas pulgas hay en perros de pradera en una colonia, la variable aleatoria es el número de pulgas en un perro de pradera en una colonia.
Ahora supongamos que pones todos los valores de la variable aleatoria junto con la probabilidad de que esa variable aleatoria se produzca. Entonces podrías tener una distribución como antes, pero ahora se llama distribución de probabilidad ya que involucra probabilidades. Una distribución de probabilidad es una asignación de probabilidades a los valores de la variable aleatoria. La abreviatura de pdf se utiliza para una función de distribución de probabilidad.
Para distribuciones de probabilidad,\(0 \leq P(x) \leq 1 \operatorname{and} \sum P(x)=1\)
Ejemplo\(\PageIndex{1}\): Probability Distribution
El Censo de Estados Unidos de 2010 encontró la posibilidad de que un hogar tenga cierto tamaño. Los datos están en Ejemplo\(\PageIndex{1}\) (“Hogares por edad”, 2013).
| Tamaño del hogar | 1 | 2 | 3 | 4 | 5 | 6 | 7 o más |
| Probabilidad | 26.7% | 33.6% | 15.8% | 13.7% | 6.3% | 2.4% | 1.5% |
Solución
En este caso, la variable aleatoria es x = número de personas en un hogar. Esta es una variable aleatoria discreta, ya que estás contando el número de personas en un hogar.
Esta es una distribución de probabilidad ya que tienes el valor x y las probabilidades que van con él, todas las probabilidades están entre cero y uno, y la suma de todas las probabilidades es una.
Se puede dar una distribución de probabilidad en forma de tabla (como en Ejemplo\(\PageIndex{1}\)) o como una gráfica. El gráfico parece un histograma. Una distribución de probabilidad es básicamente una distribución de frecuencia relativa basada en una muestra muy grande.
Ejemplo\(\PageIndex{2}\) graphing a probability distribution
El Censo de Estados Unidos de 2010 encontró la posibilidad de que un hogar tenga cierto tamaño. Los datos se encuentran en la tabla (“Hogares por edad”, 2013). Dibuja un histograma de la distribución de probabilidad.
| Tamaño del hogar | 1 | 2 | 3 | 4 | 5 | 6 | 7 o más |
| Probabilidad | 26.7% | 33.6% | 15.8% | 13.7% | 6.3% | 2.4% | 1.5% |
Solución
Variable aleatoria de estado:
x = número de personas en un hogar
Se dibuja un histograma, donde los valores x están en el eje horizontal y son los valores x de las clases (para la categoría 7 o más, simplemente llámalo 7). Las probabilidades están en el eje vertical.
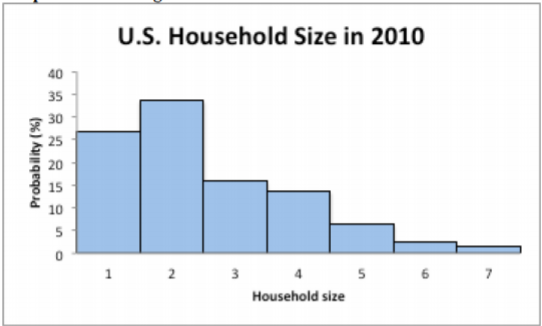.png)
Observe que esta gráfica está sesgada a la derecha.
Al igual que con cualquier conjunto de datos, se puede calcular la media y la desviación estándar. En problemas que involucran una función de distribución de probabilidad (pdf), se considera la distribución de probabilidad la población a pesar de que el pdf en la mayoría de los casos proviene de repetir un experimento muchas veces. Esto se debe a que está utilizando los datos de experimentos repetidos para estimar la probabilidad verdadera. Dado que un pdf es básicamente una población, la media y desviación estándar que se calculan son en realidad los parámetros poblacionales y no los estadísticos muestrales. La notación utilizada es la misma que la notación para la media poblacional y la desviación estándar poblacional que se utilizó en el capítulo 3.
Nota
La media se puede considerar como el valor esperado. Es el valor que esperas obtener si las pruebas se repitieran infinitas veces. El valor medio o esperado no necesita ser un número entero, aunque los posibles valores de x sean números enteros.
Para una función de distribución de probabilidad discreta,
El valor medio o esperado es\(\mu=\sum x P(x)\)
La varianza es\(\sigma^{2}=\sum(x-\mu)^{2} P(x)\)
La desviación estándar es\(\sigma=\sqrt{\sum(x-\mu)^{2} P(x)}\)
donde x = el valor de la variable aleatoria y P (x) = la probabilidad correspondiente a un valor x particular.
Ejemplo\(\PageIndex{3}\): Calculating mean, variance, and standard deviation for a discrete probability distribution
El Censo de Estados Unidos de 2010 encontró la posibilidad de que un hogar tenga cierto tamaño. Los datos se encuentran en la tabla (“Hogares por edad”, 2013).
| Tamaño del hogar | 1 | 2 | 3 | 4 | 5 | 6 | 7 o más |
| Probabilidad | 26.7% | 33.6% | 15.8% | 13.7% | 6.3% | 2.4% | 1.5% |
- Encuentra la media
- Encuentra la varianza
- Encuentra la desviación estándar
- Utilice un TI-83/84 para calcular la media y la desviación estándar
- Usando R para calcular la media
Solución
Variable aleatoria de estado:
x= número de personas en un hogar
a. para encontrar la media es más fácil simplemente usar una tabla como se muestra a continuación. Considera que la categoría 7 o más es sólo 7. La fórmula para la media dice multiplicar el valor x por el valor P (x), así que agrega una fila a la tabla para este cálculo. También convierta todos los P (x) a forma decimal.
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| P (x) | 0.267 | 0.336 | 0.158 | 0.137 | 0.063 | 0.024 | 0.015 |
| xP (x) | 0.267 | 0.672 | 0.474 | 0.548 | 0.315 | 0.144 | 0.098 |
Ahora suma la nueva fila y obtienes la respuesta 2.525. Esta es la media o el valor esperado,\(\mu\) = 2.525 personas. Esto significa que se espera que un hogar en Estados Unidos tenga 2.525 personas en él. Ahora claro que no puedes tener a media persona, pero lo que esto te dice es que esperas que un hogar tenga ya sea 2 o 3 personas, con un poco más de hogares de 3 personas que hogares de 2 personas.
b. para encontrar la varianza, nuevamente es más fácil usar una versión de tabla que intentar solo la fórmula en una línea. Mirando la fórmula, notarás que la primera operación que debes hacer es restar la media de cada valor x. Entonces cuadras cada uno de estos valores. Entonces multiplicas cada una de estas respuestas por la probabilidad de cada valor x. Por último se suman todos estos valores.
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| P (x) | 0.267 | 0.336 | 0.158 | 0.137 | 0.063 | 0.024 | 0.015 |
| \(x-\mu\) | -1.525 | -0.525 | 0.475 | 1.475 | 2.475 | 3.475 | 4.475 |
| \((x-\mu)^{2}\) | 2.3256 | 0.2756 | 0.2256 | 2.1756 | 6.1256 | 12.0756 | 20.0256 |
| \((x-\mu)^{2} P(x)\) | 0.6209 | 0.0926 | 0.0356 | 0.2981 | 0.3859 | 0.2898 | 0.3004 |
Ahora sume la última fila para encontrar la varianza,\(\sigma^{2}=2.02375 \text { people }^{2}\). (Nota: intenta no redondear demasiado tus números para que no estés creando un error de redondeo en tu respuesta. Los números de la tabla anterior se redondearon por limitaciones de espacio, pero la respuesta se calculó utilizando muchos decimales).
c. Para encontrar la desviación estándar, basta con tomar la raíz cuadrada de la varianza,\(\sigma=\sqrt{2.023375} \approx 1.422454\) las personas. Esto significa que se puede esperar que un hogar estadounidense tenga 2.525 personas en él, con una desviación estándar de 1.42 personas.
d. Vaya al menú STAT y, a continuación, al menú Editar. Escriba los valores de x en L1 y los valores de P (x) en L2. Después entra en el menú STAT, luego al menú CALC. Elija 1:1 -Var Stats. Esto pondrá 1-Var Stats en la pantalla de inicio. Ahora escriba L1, L2 (hay una coma entre L1 y L2) y luego presione ENTRAR. Si tiene el sistema operativo más nuevo en el TI-84, entonces su entrada será ligeramente diferente. Verá la salida en la Figura\(\PageIndex{1}\).
.png)
La media es de 2.525 personas y la desviación estándar es de 1.422 personas.
e. El comando estaría ponderado.media (x, p). Entonces, para este ejemplo, el proceso se vería así:
x<-c (1, 2, 3, 4, 5, 6, 7)
p<-c (0.267, 0.336, 0.158, 0.137, 0.063, 0.024, 0.015)
pesado.media (x, p)
Salida:
[1] 2.525
Entonces la media es 2.525.
Para encontrar la desviación estándar, necesitarías programar el proceso en R. Así que es más fácil simplemente hacerlo usando la fórmula.
Ejemplo\(\PageIndex{4}\) Calculating the expected value
En la lotería de Arizona llamada Pick 3, un jugador paga $1 y luego elige un número de tres dígitos. Si esos tres números son escogidos en ese orden específico la persona gana $500. ¿Cuál es el valor esperado en este juego?
Solución
Para encontrar el valor esperado, primero es necesario crear la distribución de probabilidad. En este caso, la variable aleatoria x = ganancias. Si eliges los números correctos en el orden correcto, entonces ganas $500, pero pagaste $1 para jugar, así que en realidad ganas 499 dólares. Si no escogiste los números correctos, pierdes el $1, el valor x es -$1. También necesitas la probabilidad de ganar y perder. Ya que estás escogiendo un número de tres dígitos, y por cada dígito hay 10 números que puedes escoger con cada uno independientemente de los demás, puedes usar la regla de multiplicación. Para ganar, hay que elegir los números correctos en el orden correcto. El primer dígito, eliges 1 número de 10, el segundo dígito eliges 1 número de 10 y el tercer dígito eliges 1 número de 10. La probabilidad de elegir el número correcto en el orden correcto es\(\dfrac{1}{10} * \dfrac{1}{10} * \dfrac{1}{10}=\dfrac{1}{1000}=0.001\). La probabilidad de perder (no ganar) sería\(1-\dfrac{1}{1000}=\dfrac{999}{1000}=0.999\). Poner esta información en una tabla ayudará a calcular el valor esperado.
| Ganar o perder | x | P (x) | xP (x) |
| Gana | $499 | 0.001 | $0.499 |
| Pierde | -$1 | 0.999 | -$0.999 |
Ahora suma los dos valores juntos y tienes el valor esperado. Lo es\(\$ 0.499+(-\$ 0.999)=-\$ 0.50\). A la larga, esperarás perder $0.50. Dado que el valor esperado no es 0, entonces este juego no es justo. Ya que pierdes dinero, Arizona gana dinero, razón por la cual tienen la lotería.
La razón por la que se estudia la probabilidad en la estadística es para ayudar en la toma de decisiones en la estadística inferencial. Para entender cómo se hace eso se necesita el concepto de un evento raro.
Definición\(\PageIndex{1}\): Rare Event Rule for Inferential Statistics
Si, bajo una suposición dada, la probabilidad de un evento observado en particular es extremadamente pequeña, entonces puede concluir que la suposición probablemente no sea correcta.
Un ejemplo de esto es supongamos que rozas un dado justo supuesto 1000 veces y obtienes un seis 600 veces, cuando solo deberías haber rodado un seis alrededor de 160 veces, entonces deberías creer que tu suposición de que es un dado justo es falso.
Determinar si un evento es inusual
Si está buscando un valor de x para una variable discreta, y la P (la variable tiene un valor de x o más) < 0.05, entonces puede considerar la x como un valor inusualmente alto. Otra forma de pensar en esto es si la probabilidad de obtener un valor tan alto es menor a 0.05, entonces el evento de obtener el valor x es inusual.
De igual manera, si la P (la variable tiene un valor de x o menos) < 0.05, entonces se puede considerar esto como un valor inusualmente bajo. Otra forma de pensar en esto es si la probabilidad de obtener un valor tan pequeño como x es menor de 0.05, entonces el evento x se considera inusual.
¿Por qué es “x o más” o “x o menos” en lugar de solo “x” cuando estás determinando si un evento es inusual? Considera este ejemplo: tú y tu amigo salen a almorzar todos los días. En lugar de volverse holandés (cada uno pagando su propio almuerzo), decides voltear una moneda, y el perdedor paga por ambos. Tu amigo parece estar ganando con más frecuencia de lo que esperarías, así que quieres determinar si esto es inusual antes de decidir cambiar la forma en que pagas el almuerzo (o acusar a tu amigo de hacer trampa). El proceso de cómo calcular estas probabilidades se presentará en la siguiente sección sobre la distribución binomial. Si tu amigo ganó 6 de cada 10 almuerzos, la probabilidad de que eso suceda resulta ser de aproximadamente 20.5%, no inusual. La probabilidad de ganar 6 o más es de aproximadamente 37.7%. Pero, ¿qué pasa si tu amigo ganó 501 de 1,000 almuerzos? ¡Eso no parece tan improbable! La probabilidad de ganar 501 o más almuerzos es de aproximadamente 47.8%, y eso es consistente con tu corazonada de que esto no es tan inusual. Pero la probabilidad de ganar exactamente 501 almuerzos es mucho menor, sólo alrededor del 2.5%. Por eso la probabilidad de obtener exactamente ese valor no es la pregunta correcta: debes preguntar la probabilidad de obtener ese valor o más (o ese valor o menos del otro lado).
El valor 0.05 se explicará más adelante, y no es el único valor que puedes usar.
Ejemplo\(\PageIndex{5}\) is the event unusual
El Censo de Estados Unidos de 2010 encontró la posibilidad de que un hogar tenga cierto tamaño. Los datos se encuentran en la tabla (“Hogares por edad”, 2013).
| Tamaño del hogar | 1 | 2 | 3 | 4 | 5 | 6 | 7 o más |
| Probabilidad | 26.7% | 33.6% | 15.8% | 13.7% | 6.3% | 2.4% | 1.5% |
- ¿Es inusual que un hogar tenga seis personas en la familia?
- Si te encontraras con muchas familias que tenían seis personas en la familia, ¿qué pensarías?
- ¿Es inusual que un hogar tenga cuatro personas en la familia?
- Si te encontraras con una familia que tiene cuatro personas en ella, ¿qué pensarías?
Solución
Variable aleatoria de estado:
x= número de personas en un hogar
a. Para determinar esto, es necesario mirar las probabilidades. No obstante, no se puede simplemente mirar la probabilidad de seis personas. Es necesario mirar la probabilidad de que x sea seis o más personas o la probabilidad de que x sea seis o menos personas. El
\(\begin{aligned} P(x \leq 6) &=P(x=1)+P(x=2)+P(x=3)+P(x=4)+P(x=5)+P(x=6) \\ &=26.7 \%+33.6 \%+15.8 \%+13.7 \%+6.3 \%+2.4 \% \\ &=98.5 \% \end{aligned}\)
Dado que esta probabilidad es superior al 5%, entonces seis no es un valor inusualmente bajo. El
\(\begin{aligned} P(x \geq 6) &=P(x=6)+P(x \geq 7) \\ &=2.4 \%+1.5 \% \\ &=3.9 \% \end{aligned}\)
Dado que esta probabilidad es inferior al 5%, entonces seis es un valor inusualmente alto. Es inusual que un hogar tenga seis personas en la familia.
b. Como es inusual que una familia tenga seis personas en ella, entonces puede pensar que o bien el tamaño de las familias está aumentando a partir de lo que era o que se encuentra en un lugar donde las familias son más grandes que en otras ubicaciones.
c. Para determinar esto, es necesario mirar las probabilidades. Nuevamente, mira la probabilidad de que x sea cuatro o más o la probabilidad de que x sea cuatro o menos. El
\(\begin{aligned} P(x \geq 4) &=P(x=4)+P(x=5)+P(x=6)+P(x=7) \\ &=13.7 \%+6.3 \%+2.4 \%+1.5 \% \\ &=23.9 \% \end{aligned}\)
Dado que esta probabilidad es superior al 5%, cuatro no es un valor inusualmente alto. El
\(\begin{aligned} P(x \leq 4) &=P(x=1)+P(x=2)+P(x=3)+P(x=4) \\ &=26.7 \%+33.6 \%+15.8 \%+13.7 \% \\ &=89.8 \% \end{aligned}\)
Dado que esta probabilidad es superior al 5%, cuatro no es un valor inusualmente bajo. Así, cuatro no es un tamaño inusual de una familia.
d. Como no es inusual que una familia tenga cuatro miembros, entonces no pensarías que nada anda mal.
Testo
Ejercicio\(\PageIndex{1}\)
- Eyeglassomatic fabrica anteojos para diferentes minoristas. El número de días que lleva arreglar defectos en una lente y la probabilidad de que tarde ese número de días están en la tabla.
Número de días Probabilidades 1 24.9% 2 10.8% 3 9.1% 4 12.3% 5 13.3% 6 11.4% 7 7.0% 8 4.6% 9 1.9% 10 1.3% 11 1.0% 12 0.8% 13 0.6% 14 0.4% 15 0.2% 16 0.2% 17 0.1% 18 0.1% Cuadro\(\PageIndex{8}\): Número de Días para Corregir Defectos
a. Indicar la variable aleatoria.
b. Dibujar un histograma del número de días para corregir defectos
c. Encontrar el número medio de días para corregir defectos.
d. Encontrar la varianza para el número de días para corregir defectos.
e. Encontrar la desviación estándar para el número de días para corregir defectos.
f. encontrar la probabilidad de que una lente tardará al menos 16 días en hacer una corrección del defecto.
g. ¿Es inusual que una lente tarde 16 días en reparar un defecto?
h. Si toma 16 días para que las gafas sean reparadas, ¿qué pensarías? - Supongamos que tienes un experimento donde volteas una moneda tres veces. Después se cuenta el número de cabezas.
- Afirma la variable aleatoria.
- Escriba la distribución de probabilidad para el número de cabezas.
- Dibuja un histograma para el número de cabezas.
- Encuentra el número medio de cabezas.
- Encuentra la varianza para el número de cabezas.
- Encuentra la desviación estándar para el número de cabezas.
- Encuentra la probabilidad de tener dos o más cabezas.
- ¿Es inusual que voltee dos cabezas?
- La lotería de Ohio tiene un juego llamado Pick 4 donde un jugador paga $1 y elige un número de cuatro dígitos. Si los cuatro números aparecen en el orden que escogiste, entonces ganas $2,500. ¿Cuál es tu valor esperado?
- Un lavavajillas LG, que cuesta 800 dólares, tiene un 20% de posibilidades de necesitar ser reemplazado en los primeros 2 años de compra. Una garantía extendida de dos años cuesta $112.10 en un lavavajillas. ¿Cuál es el valor esperado de la garantía extendida suponiendo que se sustituya en los primeros 2 años?
- Contestar
-
1. a. Ver soluciones, b. Ver soluciones, c. 4.175 días, d. 8.414375\(\text { days }^{2}\), e. 2.901 días, f. 0.004, g. Ver soluciones, h. Ver soluciones
3. -$0.75


