5.2: Distribución binomial de Probabilidad
- Page ID
- 149718
En la sección 5.1 se introdujo el concepto de distribución de probabilidad. El enfoque de la sección fue en distribuciones discretas de probabilidad (pdf). Para encontrar el pdf de una situación, generalmente necesitabas llevar a cabo el experimento y recolectar datos. Entonces se pueden calcular las probabilidades experimentales. Normalmente no se pueden calcular las probabilidades teóricas en su lugar. No obstante, existen ciertos tipos de experimentos que permiten calcular la probabilidad teórica. Uno de esos tipos se llama Experimento Binomial.
Propiedades de un experimento binomial (o ensayo de Bernoulli)
- Número fijo de ensayos, n, lo que significa que el experimento se repite un número específico de veces.
- Los n ensayos son independientes, lo que significa que lo que sucede en un ensayo no influye en los resultados de otros ensayos.
- Sólo hay dos resultados, que se llaman éxito y fracaso.
- La probabilidad de éxito no cambia de un ensayo a otro, donde p = probabilidad de éxito y q = probabilidad de fracaso, q = 1- p.
Si sabes que tienes un experimento binomial, entonces puedes calcular las probabilidades binomiales. Esto es importante porque las probabilidades binomiales aparecen a menudo en la vida real. Ejemplos de experimentos binomiales son:
- Tira una moneda justa diez veces, y encuentra la probabilidad de obtener dos cabezas.
- Pregunta a veinte personas en clase, y busca la probabilidad de que más de la mitad sean mujeres?
- Disparar cinco flechas a un objetivo, y encontrar la probabilidad de golpearlo cinco veces?
Para desarrollar el proceso de cálculo de las probabilidades en un experimento binomial, considere Ejemplo\(\PageIndex{1}\).
Ejemplo\(\PageIndex{1}\): Deriving the Binomial Probability Formula
Supongamos que se le da una prueba de opción múltiple de 3 preguntas. Cada pregunta tiene 4 respuestas y sólo una es correcta. Supongamos que quieres encontrar la probabilidad de que solo puedas adivinar las respuestas y obtener 2 preguntas bien. (Los maestros hacen esto todo el tiempo cuando hacen una prueba de opción múltiple para ver si los alumnos aún pueden aprobar sin estudiar. En la mayoría de los casos los estudiantes no pueden.) Para ayudar con la idea de que vas a adivinar, supongamos que la prueba es en marciano.
- ¿Cuál es la variable aleatoria?
- ¿Es esto un experimento binomial?
- ¿Cuál es la probabilidad de obtener 2 preguntas bien?
- ¿Cuál es la probabilidad de acertar a cero, a uno a la derecha y a los tres a la derecha?
Solución
a. x = número de respuestas correctas
b.
- Hay 3 preguntas, y cada pregunta es un juicio, por lo que hay un número fijo de juicios. En este caso, n = 3.
- Acertar la primera pregunta no afecta a que la segunda o tercera cuestión sea correcta, por lo que los juicios son independientes.
- O haces bien la pregunta o la entiendes mal, así que solo hay dos resultados. En este caso, el éxito es acertar la pregunta.
- La probabilidad de acertar una pregunta es una de cada cuatro. Esto es lo mismo para cada juicio ya que cada pregunta tiene 4 respuestas. En este caso,\(p=\dfrac{1}{4} \text { and } q=1-\dfrac{1}{4}=\dfrac{3}{4}\)
Se trata de un experimento binomial, ya que se cumplen todas las propiedades.
c. Para responder a esta pregunta, comience con el espacio muestral. SS = {RRR, RRW, RWR, WRR, WWR, WRW, RWW, WWW}, donde RRW significa que haces bien la primera pregunta, la segunda pregunta correcta y la tercera pregunta incorrecta. Lo mismo es similar para los demás resultados.
Ahora el espacio para eventos para acertar a 2 es {RRW, RWR, WRR}. Lo que hiciste en el capítulo cuatro fue sólo para encontrar tres divididos por ocho. No obstante, esto no sería correcto en este caso. Eso se debe a que la probabilidad de hacer una pregunta correcta es diferente a la de equivocarse en una pregunta. ¿Qué más puedes hacer?
Mira solo P (RRW) por el momento. De nuevo, eso significa P (RRW) = P (R en la 1ª, R en la 2ª y W en la 3ª)
Dado que los ensayos son independientes, entonces P (RRW) = P (R el 1º, R el 2do y W el 3º) = P (R el 1º) * P (R el 2º) * P (W el 3º)
Simplemente multiplique p * p * q
\(P(\mathrm{RRW})=\dfrac{1}{4} * \dfrac{1}{4} * \dfrac{3}{4}=\left(\dfrac{1}{4}\right)^{2}\left(\dfrac{3}{4}\right)^{1}\)
Lo mismo es cierto para P (RWR) y P (WRR). Para encontrar la probabilidad de 2 respuestas correctas, basta con sumar estas tres probabilidades juntas. Obtienes
\(\begin{aligned} P(2 \text { correct answers }) &=P(\mathrm{RRW})+P(\mathrm{RWR})+P(\mathrm{WRR}) \\ &=\left(\dfrac{1}{4}\right)^{2}\left(\dfrac{3}{4}\right)^{1}+\left(\dfrac{1}{4}\right)^{2}\left(\dfrac{3}{4}\right)^{1}+\left(\dfrac{1}{4}\right)^{2}\left(\dfrac{3}{4}\right)^{1} \\ &=3\left(\dfrac{1}{4}\right)^{2}\left(\dfrac{3}{4}\right)^{1} \end{aligned}\)
d. Podrías pasar por el mismo argumento que hiciste anteriormente y llegar a lo siguiente:
| r derecha | P (r derecha) |
|---|---|
| 0 Derecha | \(1^{*}\left(\dfrac{1}{4}\right)^{0}\left(\dfrac{3}{4}\right)^{3}\) |
| 1 derecha | \(3^{*}\left(\dfrac{1}{4}\right)^{1}\left(\dfrac{3}{4}\right)^{2}\) |
| 2 derecha | \(3 *\left(\dfrac{1}{4}\right)^{2}\left(\dfrac{3}{4}\right)^{1}\) |
| 3 derecha | \(1^{*}\left(\dfrac{1}{4}\right)^{3}\left(\dfrac{3}{4}\right)^{0}\) |
Ojalá veas el patrón que resulta. Ya puedes escribir la fórmula general para las probabilidades de un experimento Binomial
Primero, la variable aleatoria en un experimento binomial es x = número de éxitos. Ten cuidado, un éxito no siempre es algo bueno. A veces un éxito es algo que es malo, como encontrar un defecto. Un éxito solo significa que observaste el resultado que querías que sucediera.
Definición\(\PageIndex{1}\)
La fórmula binomial para la probabilidad de r éxitos en n ensayos es
\(P(x=r)=_{n} C_{r} p^{r} q^{n \cdot r} \text { where }_{n} C_{r}=\dfrac{n !}{r !(n-r) !}\)
El\(_{n} C_{r}\) es el número de combinaciones de n cosas tomando r a la vez. Se lee “n elige r”. Algunas otras notaciones comunes para n eligen r son\(C_{n, r}\), y\(\left( \begin{array}{l}{n} \\ {r}\end{array}\right)\). n! significa que se está multiplicando\(n^{*}(n-1)^{*}(n-2)^{*} \dots^{*} 2^{*} 1\). A modo de ejemplo,\(5 !=5^{*} 4^{*} 3^{*} 2^{*} 1=120\).
Al resolver problemas, asegúrate de definir tu variable aleatoria e indicar qué son n, p, q y r. Sin hacer esto, los problemas son mucho más difíciles.
Ejemplo\(\PageIndex{2}\): Calculating Binomial Probabilities
Al mirar el color de ojos de una persona, resulta que el 1% de las personas en el mundo tiene ojos verdes (“Qué porcentaje de”, 2013). Considera un grupo de 20 personas.
- Afirma la variable aleatoria.
- Argumentan que se trata de un experimento binomial.
- Encuentra la probabilidad de que ninguno tenga ojos verdes.
- Encuentra la probabilidad de que nueve tengan ojos verdes.
- Encuentra la probabilidad de que como máximo tres tengan ojos verdes.
- Encuentra la probabilidad de que a lo sumo dos tengan ojos verdes.
- Encuentra la probabilidad de que al menos cuatro tengan ojos verdes.
- En Europa, cuatro de cada veinte personas tienen ojos verdes. ¿Esto es inusual? ¿Qué te dice eso?
Solución
a. x = número de personas con ojos verdes
b.
- Hay 20 personas, y cada persona es un juicio, por lo que hay un número fijo de juicios. En este caso,\(n = 20\).
- Si asumes que cada persona del grupo se elige al azar el color de ojos de una persona no afecta el color de ojos de la siguiente persona, así los ensayos son independientes.
- O una persona tiene ojos verdes o no tiene ojos verdes, por lo que solo hay dos resultados. En este caso, el éxito es que una persona tiene ojos verdes.
- La probabilidad de que una persona tenga ojos verdes es de 0.01. Esto es lo mismo para cada juicio ya que cada persona tiene las mismas posibilidades de tener ojos verdes. p = 0.01 y q = 1 - 0.01 = 0.99
c.\(P(x=0)=_{20} C_{0}(0.01)^{0}(0.99)^{20-0} \approx 0.818\)
d.\(P(x=9)=_{20} C_{9}(0.01)^{9}(0.99)^{20-9} \approx 1.50 \times 10^{-13} \approx 0.000\)
e. a lo sumo tres significa que tres es el valor más alto que tendrá. Encuentra que la probabilidad de x es menor o igual a tres.
\(\begin{aligned} P(x \leq 3) &=P(x=0)+P(x=1)+P(x=2)+P(x=3) \\ &=_{20} C_{0}(0.01)^{0}(0.99)^{20}+_{20} C_{1}(0.01)^{1}(0.99)^{19} \\& +_{20}C_{2}(0.01)^{2}(0.99)^{18}+_{20}C_{3}(0.01)^{3}(0.99)^{17} \\ & \approx 0.818+0.165+0.016+0.001>0.999 \end{aligned}\)
La razón por la que la respuesta se escribe como mayor que 0.999 es porque la respuesta es en realidad 0.9999573791, y cuando eso se redondea a tres decimales obtienes 1. Pero 1 significa que el evento va a suceder, cuando en realidad hay una ligera posibilidad de que no suceda. Lo mejor es escribir la respuesta como mayor a 0.999 para representar que el número está muy cerca de 1, pero no es 1.
f.
\(\begin{aligned} P(x \leq 2) &=P(x=0)+P(x=1)+P(x=2) \\ &=_{20} C_{0}(0.01)^{0}(0.99)^{20}+_{20} C_{1}(0.01)^{1}(0.99)^{19}+_{20} C_{2}(0.01)^{2}(0.99)^{18} \\ & \approx 0.818+0.165+0.016 \approx 0.999 \end{aligned}\)
g. Al menos cuatro significa cuatro o más. Encuentra la probabilidad de que x sea mayor o igual a cuatro. Eso significaría sumar todas las probabilidades de cuatro a veinte. Esto llevaría mucho tiempo, por lo que es mejor usar la idea de complemento. El complemento de ser mayor o igual a cuatro es ser menor de cuatro. Eso significaría ser menor o igual a tres. La parte (e) tiene la respuesta para la probabilidad de ser menor o igual a tres. Sólo resta ese número de 1.
\(P(x \geq 4)=1-P(x \leq 3)=1-0.999=0.001\)
En realidad la respuesta es menor que 0.001, pero está bien escribirla de esta manera.
h. Dado que la probabilidad de encontrar cuatro o más personas con ojos verdes es mucho menor a 0.05, es inusual encontrar a cuatro personas de cada veinte con ojos verdes. Eso debería hacer que te preguntes si la proporción de personas en Europa con ojos verdes es superior al 1% para la población en general. Si esto es cierto, entonces es posible que desee preguntarse por qué los europeos tienen una mayor proporción de personas de ojos verdes. Eso por supuesto podría llevar a más preguntas.
La fórmula binomial es engorrosa de usar, por lo que puede encontrar las probabilidades mediante el uso de la tecnología. En la calculadora TI-83/84, los comandos de las calculadoras TI-83/84 cuando el número de ensayos es igual a n y la probabilidad de éxito es igual a p son\(\text{binompdf}(n, p, r)\) cuando se quiere encontrar P (x=r) y\(\text{binomcdf}(n, p, r)\) cuando se quiere encontrar\(P(x \leq r)\). Si quieres encontrar\(P(x \geq r)\), entonces usas la propiedad que\(P(x \geq r)=1-P(x \leq r-1)\), desde\(x \geq r\) y\(x<r\) o\(x \leq r-1\) son eventos complementarios. Tanto los comandos binompdf como binomcdf se encuentran en el menú DISTR/MOL. Usando R, los comandos son\(P(x=r)=\text { dbinom }(r, n, p) \text { and } P(x \leq r)=\text { pbinom }(r, n, p)\).
Ejemplo\(\PageIndex{3}\) using the binomial command on the ti-83/84
Al mirar el color de ojos de una persona, resulta que el 1% de las personas en el mundo tiene ojos verdes (“Qué porcentaje de”, 2013). Considera un grupo de 20 personas.
- Afirma la variable aleatoria.
- Encuentra la probabilidad de que ninguno tenga ojos verdes.
- Encuentra la probabilidad de que nueve tengan ojos verdes.
- Encuentra la probabilidad de que como máximo tres tengan ojos verdes.
- Encuentra la probabilidad de que a lo sumo dos tengan ojos verdes.
- Encuentra la probabilidad de que al menos cuatro tengan ojos verdes.
Solución
a. x = número de personas con ojos verdes
b. Está buscando P (x=0). Dado que este problema es x=0, usa el comando binompdf en el comando TI-83/84 o dbinom en R. En el TI83/84, va al menú DISTR.COM, selecciona el binompdf y luego escribe entre paréntesis sus valores n, p y r en su calculadora, asegurándose de usar la coma para separar los valores. El comando se verá así\(\text{binompdf}(20,.01,0)\) y al presionar ENTRAR se le dará la respuesta. (Si tienes el nuevo software en el TI-84, la pantalla se ve un poco diferente).
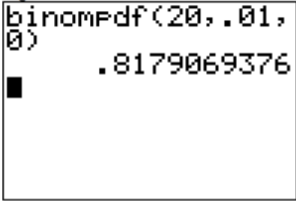.png)
En R, el comando se vería como dbinom (0, 20, 0.01)
P (x=0) = 0.8179. Así, existe un 81.8% de probabilidades de que en un grupo de 20 personas ninguna de ellas tenga ojos verdes.
c. En este caso se quiere encontrar la P (x=9). Nuevamente, utilizará el comando binompdf o el comando dbinom. Siguiendo el procedimiento anterior, tendrá binompdf (20, .01, 9) en el TI-83/84 o dbinom (9,20,0.01) en R. Su respuesta es\(P(x=9)=1.50 \times 10^{-13}\). (Recuerda cuando la calculadora te da\(1.50 E-13\) y R te da\(1.50 e-13\), así es como muestran notación científica). La probabilidad de que de una veintena de personas, nueve de ellas tengan ojos verdes es una probabilidad muy pequeña.
d. a lo sumo tres significa que tres es el valor más alto que tendrá. Encuentra la probabilidad de que x sea menor o igual a tres, que es\(P(x \leq 3)\). Esto usa el comando binomcdf en el comando TI-83/84 y pbinom en R. Se usa el comando en el TI-83/84 de binomcdf (20, .01, 3) y el comando en R de pbinom (3,20,0.01)
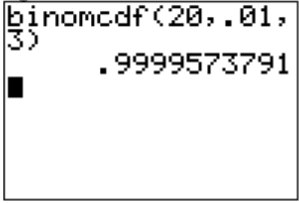.png)
Tu respuesta es 0.99996. Por lo tanto, existe una muy buena posibilidad de que en un grupo de 20 personas como máximo tres tengan ojos verdes. (Nota: no redondear esto a uno, ya que uno quiere decir que el evento va a suceder, cuando en realidad hay una ligera posibilidad de que no suceda. Lo mejor es escribir la respuesta con suficientes puntos decimales para que no se redondee a uno.
e. Usted está buscando\(P(x \leq 2)\). Nuevamente use binomcdf o pbinom. Siguiendo el procedimiento anterior tendrás\(\text{binomcdf}(20,.01,2)\) sobre el TI-83/84 y pbinom (2,20,0.01), con\(P(x \leq 2)=0.998996\). De nuevo hay una muy buena posibilidad de que como máximo dos personas en la habitación tengan ojos verdes.
f. al menos cuatro significa cuatro o más. Encuentra la probabilidad de que x sea mayor o igual a cuatro. Eso significaría sumar todas las probabilidades de cuatro a veinte. Esto llevaría mucho tiempo, por lo que es mejor usar la idea de complemento. El complemento de ser mayor o igual a cuatro es ser menor de cuatro. Eso significaría ser menor o igual a tres. La parte (e) tiene la respuesta para la probabilidad de ser menor o igual a tres. Sólo resta ese número de 1.
\(P(x \geq 4)=1-P(x \leq 3)=1-0.99996=0.00004\)También puedes encontrar esta respuesta haciendo lo siguiente en TI-83/84:
\(P(x \geq 4)=1-P(x \leq 3)=1-\text { binomcdf }(20,.01,3)=1-0.99996=0.00004\)en R:
\(P(x \geq 4)=1-P(x \leq 3)=1-\text { pbinom }(3,20,.01)=1-0.99996=0.0004\)Nuevamente, es muy poco probable que esto suceda.
Hay otras tecnologías que computarán probabilidades binomiales.
Ejemplo\(\PageIndex{4}\) calculating binomial probabilities
Según el Centro para el Control de Enfermedades (CDC), alrededor de 1 de cada 88 niños en Estados Unidos han sido diagnosticados con autismo (“CDC-data and statistics”, 2013). Supongamos que considera un grupo de 10 niños.
- Afirma la variable aleatoria.
- Argumentan que se trata de un experimento binomial.
- Encuentra la probabilidad de que ninguno tenga autismo.
- Encuentra la probabilidad de que siete tengan autismo.
- Encuentra la probabilidad de que al menos cinco tengan autismo.
- Encuentra la probabilidad de que a lo sumo dos tengan autismo.
- Supongamos que cinco niños de cada diez tienen autismo. ¿Esto es inusual? ¿Qué te dice eso?
Solución
a. x = número de niños con autismo
b.
- Hay 10 niños, y cada niño es un juicio, por lo que hay un número fijo de juicios. En este caso, n = 10.
- Si asumes que cada niño del grupo es elegido al azar, entonces si un niño tiene autismo no afecta la posibilidad de que el siguiente niño tenga autismo. Así, los juicios son independientes.
- O un niño tiene autismo o no tiene autismo, por lo que hay dos resultados. En este caso, el éxito es que un niño tenga autismo.
- La probabilidad de que un niño tenga autismo es 1/88. Esto es lo mismo para cada ensayo ya que cada niño tiene las mismas posibilidades de tener autismo. \(p=\dfrac{1}{88}\)y\(q=1-\dfrac{1}{88}=\dfrac{87}{88}\).
c. Usando la fórmula:
\(P(x=0)=_{10} C_{0}\left(\dfrac{1}{88}\right)^{0}\left(\dfrac{87}{88}\right)^{10-0} \approx 0.892\)
Usando la Calculadora TI-83/84:
\(P(x=0)=\text { binompdf }(10,1 \div 88,0) \approx 0.892\)
Usando R:
\(P(x=0)=\text { pbinom }(0,10,1 / 88) \approx 0.892\)
d. Usando la fórmula:
\(P(x=7)=_{10} C_{7}\left(\dfrac{1}{88}\right)^{7}\left(\dfrac{87}{88}\right)^{10-7} \approx 0.000\)
Usando la Calculadora TI-83/84:
\(P(x=7)=\text { binompdf }(10,1 \div 88,7) \approx 2.84 \times 10^{-12}\)
Usando R:
\(P(x=7)=\operatorname{dbinom}(7,10,1 / 88) \approx 2.84 \times 10^{-12}\)
e. Usando la fórmula:
\(\begin{aligned} P(x \geq 5) &=P(x=5)+P(x=6)+P(x=7) \\ &+P(x=8)+P(x=9)+P(x=10) \\ &=_{10} C_{5}\left(\dfrac{1}{88}\right)^{5}\left(\dfrac{78}{88}\right)^{10-5}+_{10} C_{6}\left(\dfrac{1}{88}\right)^{6}\left(\dfrac{78}{88}\right)^{10-6} \\ & +_{10}C_{7}\left(\dfrac{1}{88}\right)^{7}\left(\dfrac{78}{88}\right)^{10-7}+_{10}C_{8}\left(\dfrac{1}{88}\right)^{8}\left(\dfrac{78}{88}\right)^{10-8} \\ &+_{10}C_{9}\left(\dfrac{1}{88}\right)^{9}\left(\dfrac{78}{88}\right)^{10-9}+_{10}C_{10}\left(\dfrac{1}{88}\right)^{10}\left(\dfrac{78}{88}\right)^{10-10}\\&=0.000+0.000+0.000+0.000+0.000+0.000 \\ &=0.000 \end{aligned}\)
Usando la Calculadora TI-83/84:
Para usar la calculadora necesitas usar el complemento.
\(\begin{aligned} P(x \geq 5) &=1-P(x<5) \\ &=1-P(x \leq 4) \\ &=1-\text { binomcdf }(10,1 \div 88,4) \\ & \approx 1-0.9999999=0.000 \end{aligned}\)
Usando R:
Para usar R necesitas usar el complemento.
\(\begin{aligned} P(x \geq 5) &=1-P(x<5) \\ &=1-P(x \leq 4) \\ &=1-\text { pbinom }(4,10,1 / 88) \\ & \approx 1-0.9999999=0.000 \end{aligned}\)
Aviso, la respuesta se da como 0.000, ya que la respuesta es menor a 0.000. No escribas 0, ya que 0 significa que el evento es imposible que suceda. El evento de cinco o más es improbable, pero no imposible.
f. Usando la fórmula:
\(\begin{aligned} P(x \leq 2) &=P(x=0)+P(x=1)+P(x=2) \\ &=_{10} C_{0}\left(\dfrac{1}{88}\right)^{0}\left(\dfrac{78}{88}\right)^{10-0}+_{10} C_{1}\left(\dfrac{1}{88}\right)^{1}\left(\dfrac{78}{88}\right)^{10-1} \\ &+_{10} C_{2}\left(\dfrac{1}{88}\right)^{2}\left(\dfrac{78}{88}\right)^{10-2} \\ &=0.892+0.103+0.005>0.999 \end{aligned}\)
Usando la Calculadora TI-83/84:
\(P(x \leq 2)=\text { binomcdf }(10,1 \div 88,2) \approx 0.9998\)
Usando R:
\(P(x \leq 2)=\text { pbinom }(2,10,1 / 88) \approx 0.9998\)
g. Dado que la probabilidad de que cinco o más niños en un grupo de diez tengan autismo es mucho menor al 5%, es inusual que suceda. Si esto sucede, entonces uno puede pensar que la proporción de niños diagnosticados con autismo es en realidad más de 1/88.
Testos
Ejercicio\(\PageIndex{1}\)
- Supongamos que una variable aleatoria, x, surge de un experimento binomial. Si n = 14, y p = 0.13, encuentre las siguientes probabilidades usando la fórmula binomial.
- P (x=5)
- P (x=8)
- P (x=12)
- \(P(x \leq 4)\)
- \(P(x \geq 8)\)
- \(P(x \leq 12)\)
- Supongamos que una variable aleatoria, x, surge de un experimento binomial. Si n = 22, y p = 0.85, encuentre las siguientes probabilidades usando la fórmula binomial.
- P (x=18)
- P (x=5)
- P (x=20)
- \(P(x \leq 3)\)
- \(P(x \geq 18)\)
- \(P(x \leq 20)\)
- Supongamos que una variable aleatoria, x, surge de un experimento binomial. Si n = 10, y p = 0.70, encuentre las siguientes probabilidades usando la fórmula binomial.
- P (x=2)
- P (x=8)
- P (x=7)
- \(P(x \leq 3)\)
- \(P(x \geq 7)\)
- \(P(x \leq 4)\)
- Supongamos que una variable aleatoria, x, surge de un experimento binomial. Si n = 6, y p = 0.30, encuentre las siguientes probabilidades usando la fórmula binomial.
- P (x=1)
- P (x=5)
- P (x=3)
- \(P(x \leq 3)\)
- \(P(x \geq 5)\)
- \(P(x \leq 4)\)
- Supongamos que una variable aleatoria, x, surge de un experimento binomial. Si n = 17, y p = 0.63, encuentre las siguientes probabilidades usando la fórmula binomial.
- P (x=8)
- P (x=15)
- P (x=14)
- \(P(x \leq 12)\)
- \(P(x \geq 10)\)
- \(P(x \leq 7)\)
- Supongamos que una variable aleatoria, x, surge de un experimento binomial. Si n = 23, y p = 0.22, encuentre las siguientes probabilidades usando la fórmula binomial.
- P (x=21)
- P (x=6)
- P (x=12)
- \(P(x \leq 14)\)
- \(P(x \geq 17)\)
- \(P(x \leq 9)\)
- Aproximadamente el 10% de todas las personas son zurdas (“11 hechos poco conocidos”, 2013). Considera una agrupación de quince personas.
- Afirma la variable aleatoria.
- Argumentan que se trata de un experimento binomial Encuentra la probabilidad de que
- Ninguno es zurdo.
- Siete son zurdos.
- Al menos dos son zurdos.
- A lo sumo tres son zurdos.
- Al menos siete son zurdos.
- Siete de los últimos 15 presidentes de Estados Unidos fueron zurdos. ¿Esto es inusual? ¿Qué te dice eso?
- Según un artículo de la publicación Circulation de la American Heart Association, 24% de los pacientes que habían sido hospitalizados por un infarto agudo de miocardio no llenaron su medicación cardíaca al séptimo día de ser dados de alta (Ho, Bryson & Rumsfeld, 2009). Supongamos que hay doce personas que han sido hospitalizadas por un infarto agudo de miocardio.
- Afirma la variable aleatoria.
- Argumentan que se trata de un experimento binomial Encuentra la probabilidad de que
- Todos llenaron su medicación cardíaca.
- Siete no llenaron su medicación cardíaca.
- Ninguno llenó su medicación cardíaca.
- A lo sumo dos no llenaron su medicación cardíaca.
- Al menos tres no llenaron su medicación cardíaca.
- Al menos diez no llenaron su medicación cardíaca.
- Supongamos que de los siguientes doce pacientes dados de alta, diez no llenaron su medicación cardíaca, ¿sería esto inusual? ¿Qué te dice esto?
- Eyeglassomatic fabrica anteojos para diferentes minoristas. En marzo de 2010, probaron para ver cuántas lentes defectuosas fabricaban, y había 16.9% lentes defectuosas debido a arañazos. Supongamos que Eyeglassomatic examinó veinte anteojos.
- Afirma la variable aleatoria.
- Argumentan que se trata de un experimento binomial Encuentra la probabilidad de que
- Ninguno está rayado.
- Todos están rayados.
- Al menos tres están rayados.
- A lo sumo cinco están rayados.
- Al menos diez están rayados.
- ¿Es inusual que se rayen diez lentes? Si resulta que diez lentes de cada veinte están rayadas, ¿qué podría decirle eso sobre el proceso de fabricación?
- La proporción de M&M's marrones en un paquete de chocolate con leche es de aproximadamente 14% (Madison, 2013). Supongamos que un paquete de M&M's normalmente contiene 52 M&M's.
- Afirma la variable aleatoria.
- Argumentan que se trata de un experimento binomial Encuentra la probabilidad de que
- Seis M&M's son marrones.
- Veinticinco M&M's son marrones.
- Todos los M&M's son marrones.
- ¿Sería inusual que un paquete tuviera solo M&M's marrones? Si esto sucediera, ¿cuál pensaría que es la razón?
- Contestar
-
1. a. P (x=5) = 0.0212, b. P (x=8) =\(1.062 \times 10^{-4}\), c. P (x=12) =\(1.605 \times 10^{-9}\), d.\(P(x \leq 4)=0.973\), e.\(P(x \geq 8)=1.18 \times 10^{-4}\), f.\(P(x \leq 12)=0.99999\)
3. a.\(P(x=2)=0.0014\), b.\(P(x=8)=0.2335\), c.\(P(x=7)=0.2668\), d.\(P(x \leq 3)=0.0106\), e.\(P(x \geq 7)=0.6496\), f.\(P(x \leq 4)=0.0473\)
5. a.\(P(x=8)=0.0784\), b.\(P(x=15)=0.0182\), c.\(P(x=14)=0.0534\), d.\(P(x \leq 12)=0.8142\), e.\(P(x \geq 10)=0.7324\), f.\(P(x \leq 7)=0.0557\)
7. a. Ver soluciones, b. Ver soluciones, c. P (x=0) = 0.2059, d.\(P(x=7)=2.770 \times 10^{-4}\), e.\(P(x \geq 2)=0.4510\), f.\(P(x \leq 3)=0.944\), g.\(P(x \geq 7)=3.106 \times 10^{-4}\), h. Ver soluciones
9. a. Ver soluciones, b. Ver soluciones, c.\(P(x=0)=0.0247\), d.\(P(x=20)=3.612 \times 10^{-16}\), e.\(P(x \geq 3)=0.6812\), f.\(P(x \leq 5)=0.8926\), g.\(P(x \geq 10)=6.711 \times 10^{-4}\), h. Ver soluciones


